This paper introduces a novel ansatz in fundamental particle spectroscopy physics, building upon recent advancements in signal-to-noise distributions in space-time domains. It explores particle distributions emerging from dark matter quanta and presents a conceptual framework treating time as a rank-n-tensor wavefunction, scalarized into observable quantities. Gradient gravitational interactions linking quantum gravity to M-brane theory are incorporated onto map signal/noise metrics in a manifold matrix for particle spectra. The charge-to-mass ratios (e/m) are plotted against spin quanta for fermions, bosons, and gravitons. Graphical plots derived from these mappings suggest experimental designs for testing these hypotheses at particle accelerators, such as the Large Hadron Collider (LHC), providing insights into correlations between theoretical predictions and experimental results. The study also investigates quantum gravity, dark matter, and quantum mechanics across mesoscopic to astrophysical domains, incorporating field effects that manifest as spatial-temporal path-time evolution of matter and energy, linking past, present, and future through emergent evolutionary models, supported by mathematical graphing techniques for data processing.

Keywords: Particle Spectroscopy, Quantum Gravity, Spin Spectroscopy, Dark Matter, Charge-to-Mass Ratio.

The investigation of time as a conserved quantity has long centered on its relationship with energy. However, recent advancements have proposed time^1-9 as a critical player in particle dynamics and space-time conservation. Historical studies, such as those by^1,10,11 revealed the behavior of space-time under extreme conditions, uncovering transitions from vacuum states to superconductive phenomena. These studies underscored the importance of signal observables in understanding the space-time continuum^{1,4,12,13,7-9} Furthermore, contemporary research into dark matter has speculated that particles emerging from dark matter quanta exhibit distributions influenced by both quantum and relativistic dynamics.¹⁴ This paper extends these models by conceptualizing time as a rank-n-tensor wavefunction, which can be scalarized into observable quantities in the real universe. This approach allows for the exploration of quantum gravity through geodesic interactions and links to M-brane theory.¹⁵ Additionally, the study proposes the role of symmetrical properties at both the quantum and the macroscopic scales, exploring the role of M-branes in describing the evolution of physical states in various topological configurations.

The author’s previous research includes over 55 peer-reviewed publications that span a range of topics from point physics to the Iyer-Markoulakis Helmholtz-decomposed fields, zero-point fields, and micro-blackhole tensor matrices.^1,16-24 These advancements have explored how particle spectra could probabilistically emerge from superluminal condensates as well as how string metrics correlate with supersymmetric metrics, which may later be modified to account for asymmetric monopole interactions.^2,12,17-19 The concept of a string metrics matrix has been extended to model fermions along the cross(para)diagonal, while bosons like Higgs boson are aligned along the diagonal, providing insight into how gravity may interact with these particles; these can be considered as the condensed form of gauged metrics fields quanta.^{4,12,18,20-22} Through the Hod-PDP mechanism, the study explores how vacuum solutions for energy density and quantum gravity metrics might emerge.^{7-9,17,18,25,26,22} The development of discontinuum physics (DCP) has further broken now through quantum and relativistic limitations, addressing inconsistencies inherent in current models.²⁷

This author’s approach^2,3,5,6 treating time as a rank-6 tensor, combines mathematically algebraic vector time and arithmetic scalar time, provided a generalized transformation using major mathematical methods such as Fourier, Laplace, Hamiltonian, Lagrange, and Legendre transforms. Through this lens, the universe is considered as a "black box," where time can be extracted as a 2x2 matrix tensor. This connects to gauge fields of light and sound, setting the stage for experimental designs that measure quantum density matrices as well as scalar metrics that characterize fundamental particles. By achieving abstract derivations of signal/noise spectra in various space-time domains, this research offers new experimental techniques to probe quantum gravity and gravitons which are hypothetical particle bosons as physics conjectures.

The spin spectroscopy physics developed in this paper, combined with reference frame logistics and time conservation principles that appear in author’s recent publications, paves the way for analyzing fermions (electron, muon, tau), bosons (photons, W and Z bosons), and gravitons. Charge-to-mass ratios (e/m) versus spin quantization are plotted to identify patterns that can guide experimental designs, helping to measure the properties of particles that underpin the four fundamental forces—electromagnetic, weak nuclear, gravitational, and strong nuclear interactions. These advancements set the stage for ongoing research to discern presence of the particles within the Standard Model while filtering out supersymmetric and antiparticle interactions. Our research also bridges quantum and astrophysical phenomena, applying group theory and 4D hyperspace studies to uncover the structure of the four fundamental forces.^28-31 Astrophysical studies using Einstein-Buchdahl and Maxwell-Rindler metrics offer insights into the physical and thermodynamic properties of magnetars, black holes, and supernovae, correlating with observational data from telescopes and satellites.³²

This manuscript has been configured to organize in terms of the Section 2: Methodology & Experimental Techniques to graph real particle variables, dark matter, and plot measured actual values with a new platform of Spin Spectroscopy Physics, having known charge-to-mass ratio, spin, and spectral quantum relativistic characteristics of particles, with IT tools. Section 3 graphically represents Spin Spectroscopy PHYSICS Results & Ongoing Discussions utilizing Standard Database Programming Plotting Techniques to quantitatively analyze fermions, bosons, and the gravitons with charge-to-mass e/m values versus spin number quanta, considering quantum relativistic effects due to Thomas Precession, Bohr Magneton, and Compton shift Wavelength Electromagnetic phenomena as well as gravitational graviton bosonic effects. Section 4 then elucidates further detailed specifics observed of breakthrough graphical results to real particle accelerator measurements. Summary of the results and discussions are given in the Conclusions Section 5, with References and the Appendix towards the end of this paper article manuscript.

To explore the charge-to-mass ratio, spin, and spectral characteristics of particles, the following methodologies were employed:

Ansatz signal analysis:

This analysis investigates the quantum properties of signal observables, focusing on charge, mass, and spin. It integrates relativistic dynamics, including Thomas precession, Bohr magneton effects, and Compton wavelength electromagnetism.³³ The coupling of electromagnetic effects to gravitational gradients is crucial for understanding particle behavior in extreme states, such as in vacuum or superconductive environments.³⁴ This framework allows mapping of these signals to reveal how particles behave under quantum and relativistic conditions, particularly in relation to dark matter.

Symmetry analysis:

Symmetries of particles are examined at both quantum and macroscopic scales. Quantum-level particles may exhibit five-fold symmetry, while macroscopic crystal structures are constrained to 2-fold, 3-fold, 4-fold, and 6-fold symmetries⁴. Experimental techniques were developed to explore supersymmetry and the effects of 4D hyperspace, particularly in virtual temporal domains. The study also considers how sense-giving fields influence path-time interactions across quantum, atomic, and astrophysical domains, with implications for understanding the expansion of the universe and the formation of astronomical objects.

M-Brane theory:

This theory, especially the concept of Planck branes, is extended to describe the evolution of physical states. Open strings (longitudinal CMBR waves) and closed strings (transverse gravitational waves) are modeled to explore how particles interact with topologically curved or curled branes.^{10,14,15,4,16,17,23,24} The transformation of these strings in varying environments helps explain particle dynamics on both micro and macro scales.

Artificial intelligence and programming:

AI tools and Python programming routines were applied to facilitate data access, analysis, as well as visualization. This allowed for effective processing of charge, mass, spin, and quantum properties related to dynamical effects such as Thomas precession, Bohr magneton, as well as Compton scattering.

Signal/noise distributions and particle spectra

The results suggest that particles can be modeled as real components derived from abstract imaginary fields within a matrix wavefunction. These matrices characterize interactions in dark matter, superluminal condensates, and string theory, highlighting the role of gravitational and electromagnetic forces. Gravitational closed strings and open electromagnetic strings interact in local and global loops, producing observable particle properties such as charge, mass, and spin. These interpretations were born out of the authors’ earlier thorough abstract to real mathematical physical sciences approach deriving out of first principles, as well as algorithmic graphical simulative programming algorithm.

Charge-to-mass ratios and spin quantizations

The graphical representations of signal/noise quantum matrices [Γ_Ψ] reveal how variations in [Ψmonopoles] generate Hermitian scalar observable points in Hilbert space. The interaction between dark matter manifolds and Ψ values leads to the creation of dipoles, consistent with Born’s rules, leading to observable phenomena, including particle spectra as governed by the Hod-PDP mechanism.^{12,17,20-23,25,26,35} These phenomena are visually represented in the figures:

Graphing real particles, dark matter, & e/m versus spin quanta of fermions to gravitons

Figure 1 plotting the abstract idea of "Particle =>::<= Re {abstract, i, matrix, “firewall”} versus time" with the title "Paradoxical" shows a graph that represents a dynamic relationship over time event  between these variables. Since the concept is abstract and involves a quaternions mixture of symbols and notions (like matrices, complex numbers, and a firewall), it configures abstract plot to reflect these ideas, with a focus on changes over time, with the following choice of coordinates, having time on the x-axis. The concept of Re {abstract, i, matrix, “firewall”} on the y-axis, which mathematically interprets as a combination of complex and real components, mixing the elements (abstract, i, matrix, firewall) into a wave-like or fluctuating pattern over time accomplishes general graphics.

Explanation: (1) Time: The x-axis represents time varying from 0 to 10 seconds (or arbitrary units).

(2) Signal Components: (i) Real Part: A damped cosine wave representing the "abstract" component. (ii) Imaginary Part: A damped sine wave representing the "i" component. (iii) Matrix Fluctuations: Random noise symbolizes “matrix-like” fluctuations. (iv) Firewall Effect: A more complex interaction, modeled by a sine-cosine product to represent the "firewall" effects. (v) Plot: The combination of these components creates a fluctuating signal over time.

Output: The plot shows a fluctuating signal with a damping oscillation due to combination of the abstract elements, representing a paradoxical relationship over time.

Figure 1

Figure 1 Signal pattern Re {abstract, i, matrix, “firewall”} as a function of time coordinates.

Graphing Figure 2 key elements for the plot:

Figure 2 Mapping of Signal/noise spectra in the context of dark matter manifolds quanta.

1. Y-axis: “Γ_Ψ” (Signal/noise matrix points, scalar observable, vector density matrix in relation to wavefunction Ψ).
2. X-axis: [Ψ_Fomenko] (Quantum Probability Wavefunction dark matter bra vector).
3. Middle label: (M) = f(Γ), indicating the manifold M as a matrix of signal/noise.
4. Title: "Functional Matrix Signal/noise Point Density Matrix versus Dark Matter Probability Wavefunction Quanta."
5. X-axis Label: [Ψ_Fomenko].
6. Y-axis Label: “Γ_Ψ”.
7. Middle Box: A green box around the text (M) = f(Γ).

Explanation of the code

1. Data simulation:

1. time serves as the time variable for generating both the signal/noise matrix (Γ) and the wavefunction (Ψ).
2. Signal/noise matrix (Γ) is modeled as a decaying cosine function.
3. The wavefunction (Ψ) is modeled as a decaying sine function.
4. Dark matter probability (Ψ_Fomeenko) is simulated as the random noise to represent its quantum probabilistic nature.
5. The Γ_Ψ is calculated as the product of the signal/noise matrix and the wavefunction.

2. Plotting:

1. Γ_Ψ vs [Ψ_Fomeenko] is plotted using plt.plot().
2. A green vertical line at x=0 represents the middle of the plot. This line is used to highlight the relationship of the manifold M as a matrix of signal/noise.
3. The text (M) = f(Γ) is displayed at x=0, inside a green background box.

3. Title and labels:

1. The X-axis is labeled [Ψ_Fomeenko], representing the dark matter probability wavefunction.
2. The Y-axis is labeled “Γ_Ψ”, representing the scalar observable related to the signal/noise matrix and wavefunction.
3. The plot title is set to "Functional Matrix Signal/noise Point Density Matrix versus Dark Matter Probability Wavefunction Quanta."

4. Grid:

1. A grid is added to the plot for better readability.

The plot shows the relationship between Γ_Ψ and [Ψ_Fomeenko], with the middle of the plot marked by a green box that says (M) = f(Γ). The X-axis is labeled [Ψ_Fomeenko], whereas the Y-axis is labeled “Γ_Ψ”.

Figure 2

Spin spectroscopy physics e/m vs. spin quanta plots

Particle charge, mass, spin values from googling standard database to graph (spin, e/m)

Particle        Charge (C)           Mass (kg)           Spin (#)     

Electron        -1.602e-19            9.109e-31            0.5              

Muon            -1.602e-19            1.883e-28            0.5                          

Tau               -1.602e-19            3.167e-27             0.5                

Neutrino        0                          0                           0.5                 

Photon           0                          0                           1                    

W Boson       1.602e-19            3.183e-25              1                   

Z Boson         0                         3.310e-25              1                    

Higgs Boson  0                         2.225e-25              0                    

Graviton         0                        1e-37                     2                    

1. Graphing Figure 3 group Key elements for the plot

In Figures 3 (i) to 3(iv): Time-space plot depicting the activation of Hod-PDP mechanism across different energy scales bosons.

1. Particle properties: Each particle is characterized by charge (e), mass (m), spin (S); Planck’s constant (h), and speed of light (c) per normal values.
2. Relativistic effects: These adjust the observed behavior of the particles, especially for fermions, with:

1. Bohr magneton: The magnetic moment per unit spin for a particle is μ=2meℏ​, and this will influence the observed behavior in magnetic fields.
2. Thomas precession: This refers to the relativistic correction to the spin dynamics in a moving particle, modifying the effective magnetic moment.
3. Compton Scattering: This will be factored in when adjusting for high-energy photon-particle interactions.

Expected output:

1. Quantum Relativistic Effects:

1. Bohr magneton: Adjusts the magnetic moment of particles.
2. Thomas precession: Affects the spin in a relativistic moving particle.
3. Compton scattering: Relevant at high energy; hence, practically we can assume that the mass term does not change for low-energy cases here.

2. Charge-to-mass ratio calculations:

1. The basic formula for the charge-to-mass ratio is e/m, but we’ll show how relativistic effects influence the value, especially for high-mass particles like muons and tau leptons.

Assumptions:

1. For simplicity, we assume that relativistic effects primarily modify only the value of the observed magnetic moment but won’t alter the basic e/m ratio drastically at the energy levels typical with these particles.
2. We use proper scaling to visualize the large spread in the data.
3. The plot will show the charge-to-mass ratio on a logarithmic scale, with the x-axis representing the spin and the y-axis the charge-to-mass ratio.
4. Neutrino will be plotted at 0 for both its mass and charge-to-mass ratio since it has no charge and nearly zero mass.
5. The printed output will show the detailed properties for each particle.

Figure 3(1-4)

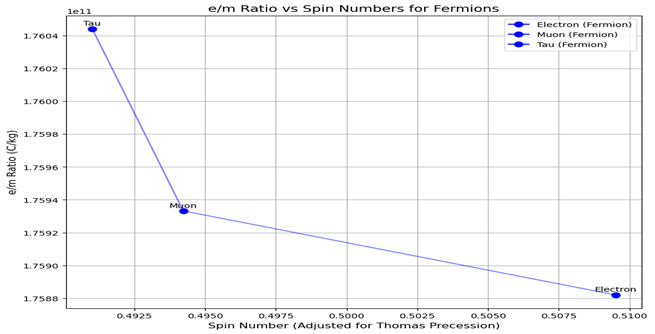
Figure 3 (i) Spin Spectroscopy Graphing PHYSICS: Charge-to-mass ratio (e/m) versus spin quanta for fermions, showing the link patterns. Visualization of the relationship between the spin and mass for particles in various quantum states.

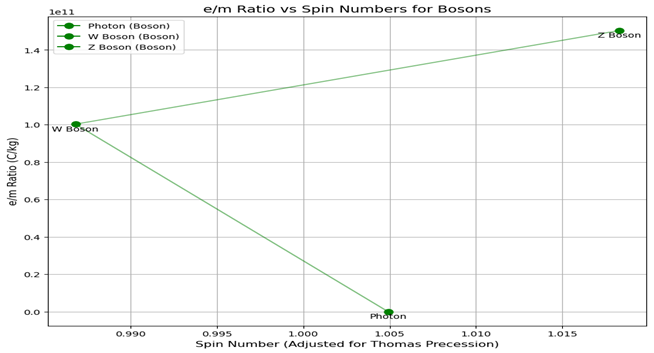
Figure 3 (ii) Spin Spectroscopy Graphing PHYSICS: Charge-to-mass ratio (e/m) versus spin quanta for bosons, showing the link patterns. Visualization of the relationship between the spin and mass for particles in various quantum states.

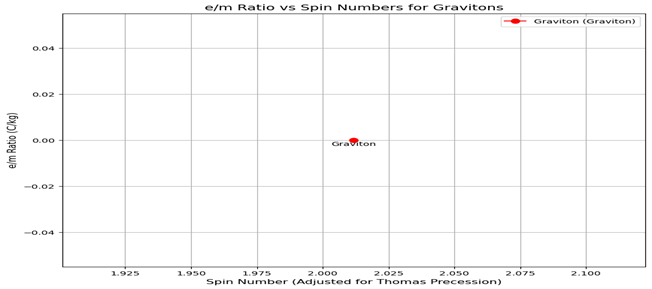
Figure 3 (iii) Spin Spectroscopy Graphing PHYSICS: Charge-to-mass ratio (e/m) versus spin quanta for gravitons, showing the link patterns. Visualization of the relationship between the spin and mass for particles in various quantum states.

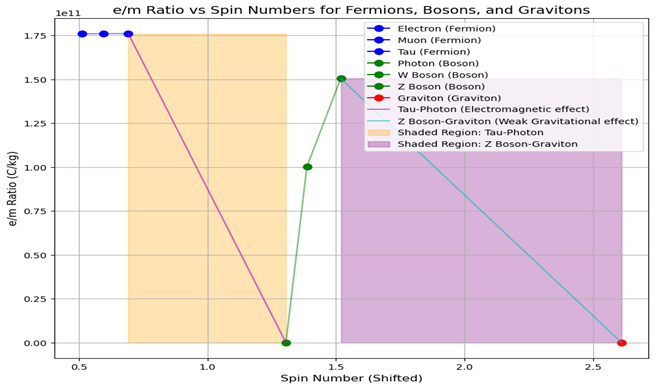
Figure 3 (iv) Comparative analysis of theoretical predictions based on Spin Spectroscopy simulations pattern of e/m charge-to-mass ratio of fermions, bosons, as well as gravitons with having quantum relativistic effects that will be hypothetically expectantly correlating with experimental data from particle accelerators futuristic predictively.

2. Graphing Figure 4 group key elements for the plot

Key Changes graphing quantum relativity action Figure 4(i) to 4(iv), referring to

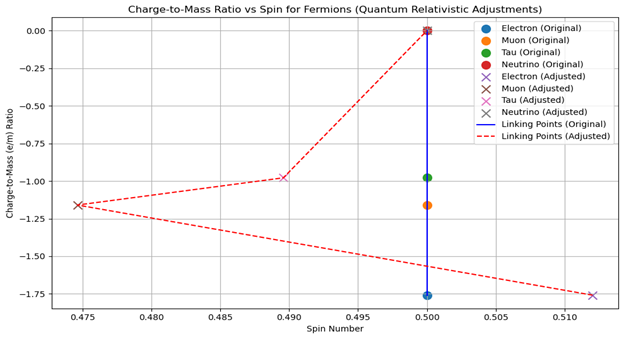
Figure 4 (i) Spin Spectroscopy Physics discerning electron, muon, and tau fermions, as well as the neutrinos with quantum relativistic adjustments, discerning differential spin charge mass particle characteristics.

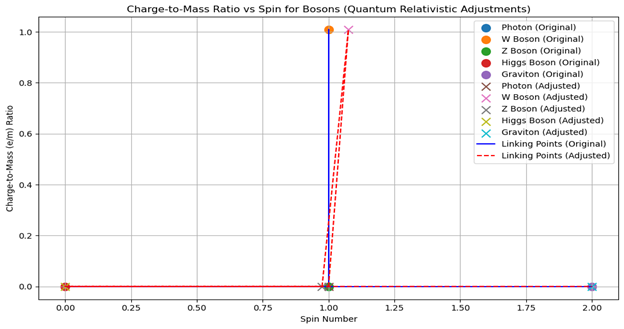
Figure 4 (ii) Spin Spectroscopy Physics discerning photons, W boson, Z boson, Higgs Bosons, gravitons with quantum relativistic adjustments, displaying differential spin charge mass particle characteristics.

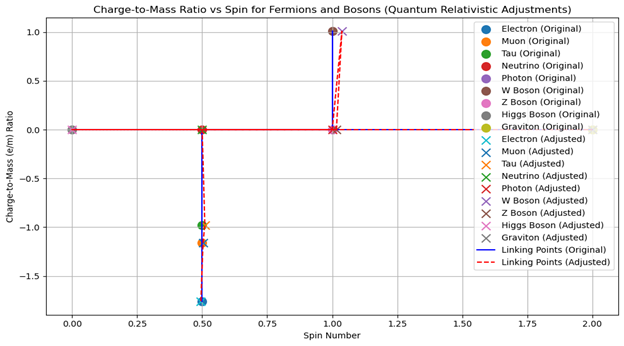
Figure 4 (iii) Spin Spectroscopy Physics discerning electron, muon, and tau fermions, as well as neutrino, Photon, W Boson, Z Boson, Higgs Boson, and the Graviton charge-to-mass e/m ratio with quantum relativistic dynamics shifting spin and e/m values as resultant of Thomas Precession, Bohr Magneton, as well as Compton electromagnetic effects.

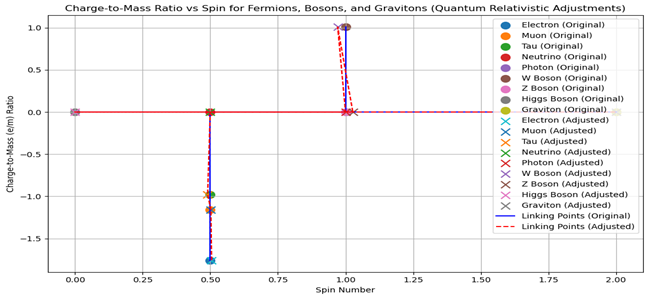
Figure 4 (iv) Spin Spectroscopy Physics discerning electron, muon, and tau fermions, as well as neutrino, Photon, W Boson, Z Boson, Higgs Boson, and the Graviton charge-to-mass e/m ratio with quantum relativistic dynamics shifting spin and e/m values as resultant of Thomas Precession, Bohr Magneton, as well as Compton electromagnetic effects. Projected conjectures would explain possibly Qquantum field interactions in mesoscopic to astrophysical regimes, helping towards electromagnetic, weak gravity, weak nuclear unification field PHYSICS.

Spin spectroscopy physics: Particle charge, mass, spin values provided above.

1. Charge-to-mass (e/m) ratio: The e/m ratio is used for each particle. For massless or neutral particles like the photon, Higgs boson, and graviton, the ratio is set to 0. The W boson has a non-zero charge-to-mass ratio, while the Z boson has a zero charge-to-mass ratio because it's electrically neutral.
2. Spin (S): Spin will be plotted on the x-axis as a characteristic quantum number of the particles. This will range from 0 (for scalar particles like the Higgs) to 1/2 (for fermions like electrons, muons, etc.) and beyond for bosons like photons (spin 1) and gravitons (spin 2).
3. Graphing: The x-axis represents the spin number (ranging from 0 for Higgs boson to 2 for the graviton). The y-axis represents the charge-to-mass ratio (with many bosons having 0 ratio due to neutral charge and massless properties). The legend differentiates between the original and adjusted points, and lines link the points for visual comparison. Markers are used to distinguish between original and adjusted points. Circles represent original points, and crosses represent adjusted points. The points are connected with lines (solid for the original points and dashed for adjusted ones). : The particles are labeled on the plot to make it clear which particle corresponds to which data point. A grid is added for better visualization, and the layout is adjusted for clarity.
4. Quantum relativistic adjustments:

1. The Bohr magneton and thomas precession will influence the motion of particles in magnetic fields, but we can simplify this and include general relativistic effects that adjust the charge-to-mass ratio for moving particles.
2. Compton scattering effects will be considered by adding regions of shading to represent the electromagnetic interaction ranges of different particles, especially fermions.
3. The spin for each particle is adjusted using a small random perturbation to simulate quantum relativistic effects (like Thomas precession). The adjusted spin is calculated by adding a random perturbation to the original spin based on the correction factor. This represents quantum relativistic effects such as Thomas precession. The program plots the charge-to-mass ratio against the spin for each particle, showing both the original values (as circles) and the adjusted values (as crosses). Lines are drawn to connect the original and adjusted points for each particle.
4. Bosons and gravitons will have shaded regions that transition between the electromagnetic effects as well as weak gravitational effects.

Figure 4(1-4)

This study contributes to the growing body of research in fundamental particle spectroscopy by introducing a novel framework that links time, quantum gravity, and M-brane theory. The analysis of charge-to-mass ratios versus spin provides valuable insights into the behavior of particles under extreme conditions. Experimental designs based on these theoretical models, particularly those involving the LHC, hold promises for verifying these hypotheses, however, based on well-known fundamental quantum measurement observational experimental values. Advancing further refinements in experimental techniques and data processing, supported by AI and programming tools, will enable more accurate measurements and deepen our understanding of the underlying forces of nature. The quantum relativistic effects considered specifically as —Thomas precession, Bohr magneton, and the Compton scattering—are shown to influence the spin and charge-to-mass ratios of particles. The findings open new possibilities for understanding dark matter, quantum gravity, and the fundamental forces across scales, from quantum to astrophysical domains. Advanced future research will focus on refining these models and comparing them with experimental data.

This study introduces a novel ansatz for particle spectroscopy, combining quantum gravity as well as M-brane theory to explore particle behavior through signal/noise distributions. These ansatz findings suggest new directions for experimental designs, particularly at particle accelerators such as the LHC. The charge-to-mass ratio and spin quantization are found to be key markers in understanding fundamental particle interactions. Theoretical models predict correlations between spin, charge-to-mass ratios, and quantum relativistic effects, providing a framework for experimental verification. Specifically, charge and spin affected by Thomas Precession, Bohr Magneton, as well as Compton electromagnetic effects, with fermions, bosons, and the gravitons linked by electromagnetic-gravitational interactions were highlighted by graphs. Symmetry analysis having Special Unitary Group spatial and temporal structures were projected to manifest within the novel ansatz Spin Spectroscopy particle PHYSICS. Future research will continue to refine these models and align them with experimental results, advancing our understanding of the fundamental forces governing the universe.

Engineering Inc. International Operational Teknet Earth Global has provided a platform launching wonderful ongoing projects that will be most useful to future human progress. Scientists worldwide specifically have contributed to the success of RESEARCHGATE forums as well as Virtual Google Meetings posted on YouTube as well per TEKNET EARTH GLOBAL SYMPOSIA (TEGS) website: https://www.youtube.com/channel/UCdUnenH0oEFiSxivgVqLYw that has successfully promoted peer-reviewed publications with ongoing project work. It is with great honor and gratitude that the author would be liking to thank collaborative international physicists ‘scientists starting with Dr. Emmanouil Markoulakis, Experimental Physicist with Hellenic Mediterranean University, Greece in mutually coauthored peer publications of many ansatzes breakthrough sciences to explore and successfully pursue quantum astrophysics. The author would too like to thank and be always grateful to Mr. Christopher O’Neill, IT Physicist with Cataphysics Group, Ireland for peer coauthored papers publications, professional graphics, and expert comments with collaborative evaluator feedback on the key contents, especially with TEKNET conference sessions discussing concepts and the graphics suggestions appreciatively exceptionally mutual project workouts ongoing. With highly engaging fruitful debates as well as discussions, the author extends profoundly high appreciation to project collaboratively engaging physicists Drs. Manuel Malaver, John Hodge, Emory Taylor, Wenzhong Zhang, Andreas Gimsa, Christian Wolf, Gerd Pommerenke, and other participating scientists. The author would be always indebted to many upcoming progressive outstanding journals who have promoted publications with excellent peer reviews of our papers’ articles.

The author received no financial support for the research, authorship, and/or publication of this article.

The authors do not have any conflict of interest.

The sole author was responsible for the conceptualization, methodology, data collection, analysis, writing, and final approval of the manuscript.

Spin Spectroscopy Physics discerns electron, muon, and tau fermions, and neutrino charge-to-mass (e/m) ratio with quantum relativistic dynamics shifting spin and e/m values as resultant of Thomas Precession, Bohr Magneton, and Compton electromagnetic effects.

Jupyter code program input output workout:

import numpy as np

import matplotlib.pyplot as plt

# Define the fermion and boson particles and their properties

particles = {

    # Fermions

    'Electron': {'spin': 1/2, 'charge_to_mass': -1.758820, 'correction_factor': 0.01, 'charge': -1.602e-19, 'mass': 9.109e-31},

    'Muon': {'spin': 1/2, 'charge_to_mass': -1.1595, 'correction_factor': 0.02, 'charge': -1.602e-19, 'mass': 1.883e-28},

    'Tau': {'spin': 1/2, 'charge_to_mass': -0.9785, 'correction_factor': 0.03, 'charge': -1.602e-19, 'mass': 3.167e-27},

    'Neutrino': {'spin': 1/2, 'charge_to_mass': 0, 'correction_factor': 0, 'charge': 0, 'mass': 0},  # Neutrino has negligible charge-to-mass ratio

    # Bosons

    'Photon': {'spin': 1, 'charge_to_mass': 0, 'correction_factor': 0, 'charge': 0, 'mass': 0},  # Photon has no charge and zero mass

    'W Boson': {'spin': 1, 'charge_to_mass': 1.008, 'correction_factor': 0.05, 'charge': 1.602e-19, 'mass': 3.183e-25},

    'Z Boson': {'spin': 1, 'charge_to_mass': 0, 'correction_factor': 0.05, 'charge': 0, 'mass': 3.310e-25},

    'Higgs Boson': {'spin': 0, 'charge_to_mass': 0, 'correction_factor': 0, 'charge': 0, 'mass': 2.225e-25},  # Higgs has no charge

    'Graviton': {'spin': 2, 'charge_to_mass': 0, 'correction_factor': 0, 'charge': 0, 'mass': 1e-37},  # Graviton has no charge and negligible mass}

# Apply quantum relativistic corrections (Bohr magneton, Thomas precession, etc.)

for particle, data in particles.items():

    # Adjusting the spin slightly due to quantum relativistic effects (Thomas precession)

    data['adjusted_spin'] = data['spin'] + np.random.normal(0, data['correction_factor'])

# Generate the plot

fig, ax = plt.subplots(figsize=(10, 6))

# Plot the original particles with charge-to-mass ratio (e/m) vs spin number

for particle, data in particles.items():

    ax.scatter(data['spin'], data['charge_to_mass'], label=f'{particle} (Original)', s=100, marker='o')

# Plot the adjusted spins after quantum relativistic corrections

for particle, data in particles.items():

    ax.scatter(data['adjusted_spin'], data['charge_to_mass'], label=f'{particle} (Adjusted)', s=100, marker='x')

# Link the points for original and adjusted scales

particle_spins_original = [data['spin'] for data in particles.values()]

particle_charge_to_mass = [data['charge_to_mass'] for data in particles.values()]

ax.plot(particle_spins_original, particle_charge_to_mass, 'b-', label='Linking Points (Original)')

# Link the points for the adjusted scale

particle_spins_adjusted = [data['adjusted_spin'] for data in particles.values()]

ax.plot(particle_spins_adjusted, particle_charge_to_mass, 'r--', label='Linking Points (Adjusted)')

# Labels and grid

ax.set_xlabel('Spin Number')

ax.set_ylabel('Charge-to-Mass (e/m) Ratio')

ax.set_title('Charge-to-Mass Ratio vs Spin for Fermions, Bosons, and Gravitons (Quantum Relativistic Adjustments)')

ax.grid(True, which='both')

# Add legend

ax.legend()

# Show plot

plt.tight_layout()

plt.show()

# Output particle properties

print(f"{'Particle':<15} {'Charge (C)':<20} {'Mass (kg)':<20} {'Spin':<10} {'Charge-to-Mass (e/m)':<25}")

for particle, data in particles.items():

    print(f"{particle:<15} {data['charge']:<20} {data['mass']:<20} {data['spin']:<10} {data['charge_to_mass']:<25}")

 Per {Figure 4 (iv): Quantum field interactions in mesoscopic to astrophysical regimes. Electromagnetic, weak gravity, weak nuclear unification field PHYSICS.}

• Particle spectra evolution under varying vacuum and superconductive conditions.
• Interaction of supersymmetry and 4D hyperspace within M-brane theory.

Hyper Unification PHYSICS gage field theoretical modeling simulations

Figure 1: Signal pattern Re {abstract, i, matrix, “firewall”} as a function of time coordinates.

Figure 2: Mapping of Signal/noise spectra in the context of dark matter manifolds quanta

Figure 3 (i): Spin Spectroscopy Graphing PHYSICS: Charge-to-mass ratio (e/m) versus spin quanta for fermions, showing the link patterns. Visualization of the relationship between the spin and mass for particles in various quantum states.

Figure 3 (ii): Spin Spectroscopy Graphing PHYSICS: Charge-to-mass ratio (e/m) versus spin quanta for bosons, showing the link patterns. Visualization of the relationship between the spin and mass for particles in various quantum states.

Figure 3 (iii): Spin Spectroscopy Graphing PHYSICS: Charge-to-mass ratio (e/m) versus spin quanta for gravitons, showing the link patterns. Visualization of the relationship between the spin and mass for particles in various quantum states.

Figure 3 (iv): Comparative analysis of theoretical predictions based on Spin Spectroscopy simulations pattern of e/m charge-to-mass ratio of fermions, bosons, as well as gravitons with having quantum relativistic effects that will be hypothetically expectantly correlating with experimental data from particle accelerators futuristic predictively.

Figure 4 (i): Spin Spectroscopy Physics discerning electron, muon, and tau fermions, as well as the neutrinos with quantum relativistic adjustments, discerning differential spin charge mass particle characteristics.

Figure 4 (ii): Spin Spectroscopy Physics discerning photons, W boson, Z boson, Higgs Bosons, gravitons with quantum relativistic adjustments, displaying differential spin charge mass particle characteristics.

Figure 4 (iii): Spin Spectroscopy Physics discerning electron, muon, and tau fermions, as well as neutrino, Photon, W Boson, Z Boson, Higgs Boson, and the Graviton charge-to-mass e/m ratio with quantum relativistic dynamics shifting spin and e/m values as resultant of Thomas Precession, Bohr Magneton, as well as Compton electromagnetic effects.

Figure 4 (iv): Spin Spectroscopy Physics discerning electron, muon, and tau fermions, as well as neutrino, Photon, W Boson, Z Boson, Higgs Boson, and the Graviton charge-to-mass e/m ratio with quantum relativistic dynamics shifting spin and e/m values as resultant of Thomas Precession, Bohr Magneton, as well as Compton electromagnetic effects. Projected conjectures would explain possibly Qquantum field interactions in mesoscopic to astrophysical regimes, helping towards electromagnetic, weak gravity, weak nuclear unification field PHYSICS.

Applying derivations mathematical physical sciences, the author has advanced over the years now,^{1-9,12,13,16-24} it is possible to transition from mathematical physics, theoretical physics onto particle astrophysics, with experimental physics showing proof of the concept, especially SPIN SPECTROSCOPY PHYSICS graphing programmable algorithm derived here.

These findings suggest that mathematical models can describe the activation of particles and their subsequent behavior, linking them to known parameters of charge, mass, and spin. As particles are mapped from abstract fields to real components in space-time, these results offer novel insights into dark matter, quantum gravity, and the mechanisms governing particle formation in the universe.

1. Iyer R. Signals/Noise Measurable Observables Limiting Temporal Spatial Domains of Reality Defining Physics. Phys Sci Biophys J. 2024;8(2):000279.
2. Iyer R. Algorithm it Quantitative Physics Coding, Quantum Astrospace Timeline. Orient J Phys Sci. 2023;8(2):0004.
3. Iyer R. Quantum Gravity Time Rank–N Tensor Collapsing Expanding Scalar Sense Time Space Matrix Signal/Noise Physics Wavefunction Operator. Phys Sci Biophys J. 2024;8(2):000271.
4. Iyer R. Quantum Astrophysics General Formals Theoretical to Experimental Gaging. In: Futuristic Trends in Physical Sciences. IIP Series. Vol 3, Book 3. 2024:253–286. ISBN: 978–93–6252–011–1.
5. Iyer R. Rank–n–Tensor PHYSICS Arithmetic Scalar Algebraic Vector Time Algorithm Matrix. Invited Speaker and Session Chairman Presentation. ICFAS2024; July 10, 2024. Online Virtual Conference.
6. Iyer R. Time Conservation Principle Versus Energy Physics. Open J Astron. 2024;2(2):000139.
7. Iyer R. Signals/Noise Measurable Observables Limiting Temporal Spatial Domains of Reality Defining Physics. Phys Sci Biophys J. 2024;8(2):000279.
8. Iyer R. An Exact New Solution of the Schrödinger Equation with a Zero Potential Energy Analogous to Fick’s Equation of Diffusion. Phys Astron Int J. 2024;8(1):59–63.
9. Iyer R. Algebra Fields Time Transformations Geometry of Space Gaging. Oral presentation at: ICFAS 2023; June 8–10, 2023; Special Session: Algebra with Applications.
10. Polchinski J. String Theory, Volume 1: An Introduction to the Bosonic String. Cambridge University Press; 1998.
11. Wheeler JA, Feynman RP. Interaction with the Absorber in Quantum Electrodynamics. Rev Mod Phys. 1945;17(2):157–181.
12. Iyer R. Configuring Observables Solving Physical Algorithm Quantum Matrix Gravity. J Mod Appl Phys. 2022;5(1):1–5.
13. Iyer R. Absolute Genesis Fire Fifth Dimension Mathematical Physics. Engineeringinc International Corporation; 2000:63. Amazon.com.
14. Bousso R, Polchinski J. Quantization of Four–Dimensional De Sitter Space. Phys Rev D. 2000;62:046004.
15. Becker K, Becker M, Schwarz JH. String Theory and M–Theory: A Modern Introduction. Cambridge University Press; 2007.
16. Iyer R. Electromagnetism Quantum PHYSICS Conservation Laws Tensor Unveiling Nonlinear Characteristics of Time. Book Chapter. (Publication in progress).
17. Iyer R. Discontinuum Critical Signal/Noise Density Matrix. Phys Sci Biophys J. 2022;6(1):000210.
18. Iyer R, O'Neill C, Malaver M. Helmholtz Hamiltonian Mechanics Electromagnetic Physics Gaging Charge Fields Having Novel Quantum Circuitry Model. Orient J Phys Sci. 2020;5(1–2):30–48.
19. Iyer R, Markoulakis E. Theory of a Superluminous Vacuum Quanta as the Fabric of Space. Phys Astron Int J. 2021;5(2):43–53.
20. Iyer R, O'Neill C, Malaver M, et al. Modeling of Gage Discontinuity Dissipative Physics. Can J Pure Appl Sci. 2022;16(1):5367–5377.
21. Iyer R, Malaver M, Taylor E. Theoretical to Experimental Design Observables General Conjectural Modeling Transforms Measurement Instrumented Physics Compendium. Res J Mod Phys. 2023;2(1):1–14.
22. Iyer R. Quantum Physical Observables with Conjectural Modeling: Paradigm Shifting Formals II: A Review. Orient J Phys Sci. 2022;7(2):50–66.
23. Iyer R. Strong Gravity Versus Weak Gravity: Fiber Transforms Gravity–Bundle–Strings: Preliminary Results. Can J Pure Appl Sci. 2023;17(2):5697–5703.
24. Iyer R. Problem solving measurement physics references entity calibrational systems. Orient J Phys Sci.
25. Hodge J. Structure and spin of the neutrino, electron, and positron. 2016;5(2):1–8.
26. Hodge J. Scalar Theory of Everything (STOE) unites the big, the small, and the four forces (GUT) by extending Newton's model. 2020.
27. Taylor E, Iyer R. Discontinuum physics leads to a table of realities for making predictions. Phys Essays. 2022;35(4):395–397.
28. O'Neill C, Iyer R. Support Vector Machine Model of the Universe. 2023. Available from:
29. O’Neill C. Dimensions of the Hyperspheric Universe. 2023.
30. O'Neill C. Isomorphism of the Modified Standard Model Particles and the Binary Octahedral Group (24–cell). 2023.
31. O’Neill C. Automorphism of the Modified Standard Model Particles from the 24–cell to the 600–cell and E8 using the Alternating Subgroup A4 and S5. 2023.
32. Malaver M, Kasmaei H, Iyer R. Magnetars and Stellar Objects: Applications in Astrophysics. Eliva Press Global Ltd.; 2022. ISBN: 978–99949–8–246–2.
33. Jackson JD. Classical Electrodynamics. 3rd ed. Wiley; 1999.
34. Gross DJ, Witten E. Superstring Theory. Phys Rep. 1985;136(1–2):1–99.
35. Hod S. Gravitational Radiation and Particle Spectrum in Quantum Gravity. Phys Rev D. 1998;57(6):3747–3750.