We present a survey of past results regarding the equilibrium and the stability of self-gravitating liquid masses, exceling the distorted spheroids structured as onion-like multi-shells rotating differentially which we recently (2021) used or modeling Jupiter and Saturn.

Keywords: liquid, equilibrium, ellipsoidal, rotation

The shape and the rotation of self-gravitating fluid masses at equilibrium has been the subject of our research for more than 40 years, a task fully achieved at UASLP. Our field is closely related to that of the equilibrium configurations, or figures, established by connoted mathematicians of the XVII and XVIII centuries shortly after relying on the gravitational potential of a homogeneous ellipsoidal mass; being a scalar quantity the potential is most useful to easy this kind of work.

A tri-dimensional ellipsoid can be generated by letting rotate an ellipse about its least axis; if two of the semi-axes are equal we obtain an oblate spheroid. The equilibrium of interest is meant as relative to a system of coordinates affixed to the rotating mass, but an inertial frame could operate as well; because the rotation is executed round the least axis, the figures are oblate, and can be characterized by their polar flattening e and the angular velocity Ω (in the unit πGρ), where ρ is the density. These masses are considered as classical and, nowadays, can be calculated with up to 100 significant digits so they are credited of exact equilibrium. The weakness of these masses is that, besides of being homogeneous (ρ = constant), they are made out of a perfect liquid, which are not to the taste of those astrophysicists that model stars. Nevertheless, Chadrasekhar¹ (NP 1983) thought otherwise and rescued them from oblivion in the late 60’s.

Boundary conditions

Since the mass self-gravitates, the equilibrium condition demands that the pressure vanishes on its boundary surface, where matter terminates, a requisite that is satisfied by a set of couples (e, Ω); for every such pair, a perfect balance occurs between the centrifugal and the gravitational forces acting on the mass, thereof resulting a figure; the complete set of such couples is known as a series.

The shape of the Earth.

The shape of the Earth raised the interest of both, Newton and Cassini, with the first claiming that it resembles an oblate spheroid, while the second assured that it was prolate; this last form, however, is unacceptable because it gives an incorrect account of the involved centripetal force. The discrepancy between these two great scientists generated a famous debate that polarized the scientific society of the epoch.

The Classical series

The series of spheroids (Maclaurin 1742), and ellipsoids (Jacobi 1834) are considered as classical, with the second branching off (bifurcating) from the former at e = 0.8127, where a neutral frequency occurs. Maclaurin himself derived a formula for Ω as a function of e, which is nonlinear: two spheroids of different e can have the same Ω.  An ellipsoid has two eccentricities: polar and equatorial. Other ellipsoidal series are: Dedekind’s, whose equilibrium is sustained by internal currents of uniform vorticity circulating along equatorial planes throughout their volume; these figures are static; Riemann’s, whose equilibrium is sustained by two motions operating at once: an internal one (as in Dedekind’s), and a solid-body rotation (as in Jacobi’s). 

Inhomogeneous masses

At UASLP, we are concerned with the equilibrium and the stability of inhomogeneous masses because they are certainly more adequate to mimic celestial objects (not necessarily stars). In our models, as in stars, the density increases towards the centre. Our first model consisted of two concentric Maclaurin spheroids, nucleus and atmosphere, with ρ_n > ρ_a (Figure 1); the body’s relative density is designated by ε [= (ρ_n – ρ_a)/ρ_a]. We study the cases of common and different Ω (in the unit 2πG ρ_a).

Figure 1 Our in-homogeneous model of two layers.

The term atmosphere is only decorative, and should not be interpreted as a real atmosphere. The boundary conditions to be satisfied are: the vanishing of the pressure (p_a = 0) at the boundary atmosphere-vacuum, on account that the mass is self-gravitating; and the continuity of the pressure (or, equivalently, of the potential) at the interface nucleus-atmosphere:  p_{n =} p_a, on account that no flow of matter must occur there. The complicated dependence of the ellipsoidal coordinate can be avoided assuming the nucleus and the atmosphere are confocal (meaning that they share the same focuses); this model has been generalized to l layers by Bizyaev et al.² Figure 2 depicts our trick for the evaluation of the potentials. When Ω_n > Ωa. a family of series (one for each ε value) results.  Example: ε = 5, e_n = 0.5, Ω_n = 0.4173, e_a = 0.2, Ω_a = 0.0138. For this figure (a stable one), the density of the nucleus is 6 times higher than that of the atmosphere.

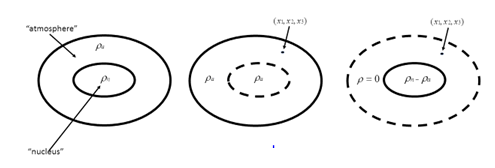
Figure 2 The trick used to evaluate the required potentials: the model (left) is replaced by the addition of two structures: the first (center), consisting of a mass completely of density ρ_a  throughout, which amounts to an interior contribution; and the second (right), consisting of a hypothetical nucleus of density ρ_n – ρ_a  surrounded by an atmosphere of zero density (that compensates the excess of mass of the former calculation) which amounts to an exterior contribution.

For Ω_n = Ω_a no figures arise, neither spheroids nor ellipsoids, which is consistent with Hamy’s theorem: a mass made up of two (or more) confocal spheroids (or, more generally, ellipsoids) rotating with common angular velocity, cannot be at equilibrium.

Our numerical results agree with Hamy’s theorem, which dates from 1900, and which was provided to us by F.Chambat (Strasbourg, France, 1990). The case of ellipsoids rotating with different angular velocities was disregarded at once because destructive interference is likely to occur between the respective velocity fields, particularly at their noses.

Stability.

The analysis of stability of the figures is carried out by means of the virial technique as developed by Chandrasekhar and Lebovitz. In our series, regimes of instability arise when the nucleus rotates very fast and so is markedly flattened; members of neutral frequency also result. As is well-known, the Jacobi series branches off (bifurcates) rom that Maclaurin member with e = 0.8127, where a neutral frequency occurs.

A plausible expectation

Because within the solution spheroids of neutral   frequency occur, it would appear that, in parallel with the homogeneous case, inhomogeneous tri-axial figures would be possible. But no such figures arise, so that our expectative was fruitless or, more exactly, only partially fulfilled (see farther on our quasi-equilibrium Riemann-type ellipsoids).

Hamy’s theorem was unknown to us until 1990, when F.Chambat warned us about it. Stimulated by the presence inhomogeneous spheroids of null frequency, we persisted on our goal of finding inhomogeneous figures with the somewhat elusive ellipsoidal shape, for which we reverted to Riemann ellipsoids of class S, which owe their equilibrium to two simultaneous motions:  an internal one in the form of currents of uniform vorticity, call it Z, plus another of uniform rigid body rotation, Ω_. To avoid a direct confrontation with Hamy’s theorem, the vorticities of the nucleus and the atmosphere were taken as different, Z2n ≠ Z2a, while the rotation was chosen Ω2n = Ω2a, otherwise the velocity fields of the nucleus and the  atmosphere would be likely to perturb one another, especially at the noses, thus destroying the equilibrium.

 The equilibrium conditions of this model produces a system of four equations, whose solution consists (let, for the moment, the rotation be ignored) of series of constant ε; each non-rotating figure must be tested individually for rotation; if the atmosphere were to be removed, the remaining core would become a Riemann ellipsoid of class S. The figures are characterized by its four eccentricities: e_n1, e_n2, e_a1, e_a2, suffix 1 (2): equatorial (polar) direction which, by confocality, reduce to three, because the confocality relation reads e_a1 / e_a2 =   e_n1 / e_n2. In addition, e_n1 > e_a1, e_n2 > e_a2.  These relations imply that the nucleus is flatter than the atmosphere in both directions: equatorial and polar; also, the figures must be oblate.

Methodology. With the angular velocity incorporated, the system of equations is G_i (ε, e_n1, e_n2, e_a2, Z²_n, Z²_a, Ω², F_n, E_n, F_a, E_a) = 0     

 i = 1-4 where Z designates the vorticity; E and F are the Legendre standard incomplete elliptic integrals of the two kinds; the solution of this system was obtained   through Newton’s iterative method.

The accuracy of the current figures, however, is far from matching that of the classical homogeneous ones, moreover, the watermelon-watermelon shape is never attained: not a single figure could be obtained (with a reasonable accuracy) having at once the ovoid shape for both, nucleus and atmosphere. Actually, the atmosphere tends to be spherical, which impels the body of a rather low rotation.  Thus, the influence of Hamy’s theorem persists, although not as severely. In spite of these two drawbacks, some figures with mixed characteristics of an ellipsoid for the nucleus, and a spheroid for the atmosphere, are worthy of mention.

Accuracy

Recall that, for the classical figures G_i~10^-100, i = 1 to 2, which our program retrieves, along with the rest of properties (potential energy, kinetic energy, angular momentum and frequencies of oscillation), as ε approaches 0.

The accuracy of these figures attains its highest level, G_i ~10^-67, when the atmosphere is so thin that their polar and equatorial eccentricities differ from those of the nucleus by, say, 45 places after the decimal point. Only so the nucleus and the atmosphere of a same figure can be neatly ellipsoidal, which is not surprising, because the body is practically homogeneous. These figures can rotate very fast. For thick atmospheres, yet practically spherical, we have G_i ~10^-50; the nucleus of these figures can be a neat ellipsoid. To construct a series of fixed ε, we let e_n1 to increase from, say, 0.0001, up to 0.9. Just a few figures (very inaccurate, though: G_i ~10^-9) were obtained closest to the ellipsoidal-ellipsoidal geometry. The rotation (as looking down from above the pole) is effected in a counter-clockwise direction, i.e., in a direct fashion; if the internal currents circulate also directly, the corresponding figures become an inhomogeneous version of a Riemann ellipsoid of class S. An example (stable):

ε = 10, e_n1 = 0.1; e_n2 = 0.8390; Z²_n  = 4.4517; e_a1 ~10^-9 , e_a2 ~10^-9 , Z²_a ~10^-30, Ω² _max~10^-25; if, in a given figure  we let (in our computer program) e_a2  to  increase, the accuracy steadily decreases to undesired levels (to G_i ~10^-13, for e_a2 ~10^-5); so this strategy is not suitable, as indeed none is for getting figures with both an ellipsoidal nucleus and an ellipsoidal atmosphere. If the currents circulate retrograde, the rotation is guaranteed. Once equilibrium figures are obtained, the next step concerns their stability.

Stability.  In common circumstances, two types of stability are distinguished: stable and unstable. A simple way for understanding this is to imagine a cone with its base lying on a frictionless table; when a force parallel to the surface is applied to the cone, it will respond by slipping a certain distance (stable); if the force is applied when the cone is placed with its tip on the table, it will fall over the table (unstable).

In the current context, the stability is studied through the virial method, which consists in multiplying Euler’s equation successively by 1, x_j, x_j x_k, ..., and then integrating over the whole considered volume. One of the quantities involved for calculating the modes of oscillation to second-harmonic is the so called super-tensor of potential energy, whose specification requires of two, rather than one, couple of indices.

The energies of the figures. Expressions for the potential energy, the kinetic energy, and the angular momentum of the figures (all in the unit GM²/a₁a₂a₃), were obtained, where M is the body’s mass, and a₁, a₂, a₃ are the semi-axes of the atmosphere; the resulting expressions are, however, too showy. 

New strategy. Up to here, the equilibrium has been established under a scheme based on Euler equation (the equivalent to Newton’s second law), and employing surface equations purely quadratic. Clearly, if we persist on obtaining ellipsoidal figures of exact equilibrium, we must desist on using quadratic surfaces. On this account, we started anew with a distorted surface, which we take as that of a regular ellipsoid with the additional term:

                  d (z⁴ / (a3)⁴ ) 

where d (> - 1/4, to assure that the surface is closed) is the distortion parameter. No relation is assumed to exist between the semi-axes of the nucleus and the atmosphere.

The equilibrium will be sought through Bernoulli’s theorem, but not in its usual presentation, rather in a generalized form suitable for an irrotational fluid (such as our current fluid is). The process of generalization lead us to a very important consequence, namely a law of rotation, with the novelty that the rotation is of a differential character (uniform rotation did not satisfy Bernoulli’s theorem), yet restricted to masses with cylindrical symmetry, namely spheroidals (so called by Jeans to distinguish them from true spheroids). The relation between the parameter of distortion d and the semi-axis a3 is

                                   ZM = (a3/√2) √(√(1 + 4d)/d - 1/d

where ZM is the polar flattening of the figures (the index M has no special meaning)

For the homogeneous case, the rotation law reads Ω = - 2 dB/dr, where B is the gravitational potential, and r is the distance to the rotation axis; by differential rotation we mean that the rate of angular velocity varies both, on the surface of the outermost shell as well as on the deeper ones. The angular velocity profile is not imposed ab initio; rather, it is a consequence of the equilibrium itself. From this law, there result series consisting of homogeneous spheroidals; when the law was extended (with the aid of Figure 2) to two shells, the result was a vast quantity of series, which are quite more involved than the homogeneous ones, because they depend on six parameters: the relative density, the relative size of the nucleus with respect to the atmosphere, the two distortion parameters, and the polar flattening of the nucleus and the atmosphere. Furthermore, the law could be successfully extended to any number of spheroidal shells, assembled in a onion-like fashion.^3,4

Besides verifying that the (squared) angular velocities (at the pole and at the equator) be positive, it must also be checked out that the true third semi-axis (the flattening ZM) of the nucleus be lower than that of the atmosphere, otherwise the nucleus would intrude the atmosphere. Spheroids proper (d = 0), both homogeneous (ε = 0) and inhomogeneous, are also possible. All of our results on equilibrium, stability and energies coincide with the known facts for the homogeneous masses in the limit as ε [= (ρ_n – ρ_a)/ρ_a] tends to zero.

It is important to realize that the angular velocities are a consequence of the equilibrium itself, rather than being imposed ad initio. Two curios results: For low ε (< 0.5), the nucleus can be prolate (an elongated distorted spheroid); no prolate atmospheres were found; equilibrium is also possible when the internal mass is less dense than the exterior one (without being necessarily unstable).

Applications

Recently, with our multi-shell masses, and taking advantage of the gravitational data provided by the Juno and Cassini missions, we succeeded in constructing models for Jupiter and Saturn (no equations of state nor magnetic fields involved), a result that has received a certain international attention.

With a variation of the above technique, we are currently working on a multi-shell model of equilibrium for the Sun, using data from the standard model; this problem, which has had a slow advance, was suggested by Martínez Herrera some months before his passing away.

15 papers published by high-standard editorials attest our work.

None.

None.

1. Chandrasekhar S. Ellipsoidal Figures of Equilibrium. New Haven, CT: Yale University Press; 1969.
2. Bizyaev IA, Borisov AV, Mamaev IS. Figures of equilibrium of an inhomogeneous self-gravitating fluid. Celest Mech Dyn Astr. 2015;123(3):269–298.
3. Cisneros JU, Martínez FJ, Montalvo JD. On the dynamical stability of ellipsoidal configurations. Am J Astron Astrophys. 2021;8(1):8-14.
4. Montalvo JD, Martínez FJ, Cisneros JU. Stability of ellipsoidal figures. Rev Mex Astron Astrofis. 1983;5:293–305.