Rubber tree (Hevea brasiliensis. Muell Arg.), an exotic deciduous rainforest tree species of Euphorbiaceae-Family. Bangladesh is indigenous to the natural forests of the Amazon valley in South America. It is one of the most important cash crops, with multipurpose uses. Now a day this tree species has drawn unique position due to the furniture making and construction work. The growth rate and yield of the species in Bangladesh are not known. Therefore, for scientific management of the forest necessity of the growth and yield models for the species were felt. The present study was made to derive mathematical models for growth and yield of this species in Bangladesh based on site indices. The models were developed through establishment of Temporary Sample Plots (TSPs) with area 0.02 ha and shape is circular and rectangular. Diameter at breast height and total height of all trees in the plots were measured. Step-wise method and all probable combinations of the independent variables method were used to select the best suited models subject to the satisfaction of the statistical and biological requirements. Models were selected to estimate the stand stocking, stand height, stand diameter, stand basal area, stand volume yield per hectare and stand biomass per hectare. The yield prediction models derived in the study could satisfactorily be used at stand age of 4.0 to 35 year. Site indices of 9.0 to 21.0 meters based on a base age of 25 years. Extrapolation over this data range is not recommended.

The prediction models developed were composed of six equations: stand mean height equation, stand Dbh equation, stand density equation, stand total volume per hectare and stand biomass per hectare yield equation. A model to estimate the number of stem per hectare based on age was also predicted. The growth and yield characteristics were estimated by regression techniques based on statistical and biological criteria. The chosen yield prediction models were verified using separate sets of data. Chi-square test, paired t-test, percent absolute deviation and 45-degree line test were used for the validation of chosen models. Biological principle of stand development was checked. The results suggest that the models were statistically and biologically acceptable. The developed models might safely use for the prediction of growth and yield of rubber tree.

Keywords: hevea brasiliensis, growth and yield, prediction, plantation and Bangladesh

Growth and yield models rely on observable and quantifiable changes, analyzed through biological principles applicable to living systems and expressed using mathematical frameworks. These principles and mathematical tools enable the separation of intricate tree interactions, whether individually or collectively, that are difficult to validate. A logical relationship is then applied to simulate the growth and yield of a forest tree or stand.^1–7 Forest growth models aim to measure forest development and are primarily used for two main purposes: forecasting the future condition of a forest and potential harvest outcomes, as well as evaluating different cultivation strategies.^3,8,9 Models can serve additional purposes, such as in education or conveying information. Depending on their intended use, modelers may prioritize either detailed physiological representation or statistical efficiency, but they typically strive to achieve both biological and statistical precision.^4,9

Most of the forest management decisions are influenced by the growth and yield of the existing stocks. Yield estimation offers insights into the condition of a specific forest stand at a given age, helping decision-makers plan forest regulation strategies and establish timber harvest schedules.^4,8,9 Additionally, information is needed to assess alternatives to the economic management of forests, such as determining the optimal rotation age.¹⁰ Growth and yield data can also evaluate forest stand performance as a fundamental source of information. Therefore, predicting growth and yield provides a direct input for other system components, particularly in Bangladeshi plantations. This study aims to develop a mathematical model for estimating the growth and yield of rubber tree plantations in Bangladesh.

The rubber tree (Hevea brasiliensis, Muell Arg.), a deciduous rainforest species from the Euphorbiaceae family, is native to the Amazon valley in South America but has become an important crop in Bangladesh. It is a versatile cash crop with multiple uses. In 1910, a few seedlings of this species were introduced to Bangladesh in the tea gardens of Baromashia, Fatikchari upazila in Chittagong district, and Amu in Sylhet district, sourced from the Calcutta Botanical Garden.¹¹ Experimental plantations began in 1954 by the Forest Department in locations like Madhupur (Tangail), Hazarikheel (Chittagong), and Tetulia (Panchagarh). In 1960, the first commercial plantation was established on 4 hectares in Raojan (Chittagong) and 12 hectares in Ramu (Cox’s Bazar). In 1962, the responsibility for rubber plantations was handed over to the Bangladesh Forest Industries Development Corporation (BFIDC), which expanded planting in Chittagong, Sylhet, Tangail, and Sherpur. Between 1962 and 1997, the Chittagong Hill Tracts Development Board (CHTDB), various multinational companies, and private entrepreneurs further developed rubber plantations. Many of these plantations are now old and underproductive, leading to continuous replacement with new ones.

The determination of the rotation age of the rubber tree is important. In the absence of a comprehensive study, the Bangladesh Forest Industries Development Corporation has set the rotation age of the species at 20-30 years. It is desired that the rotation age should have a concrete foundation. The raising of plantations is a capital-intensive business and knowledge about its rotation age is essential in weighing different alternatives and planning strategies to optimize the benefit flow. It also helps to answer the basic questions of forest management when, where, what, and how much to cut from the forest. The growth rate and yield of rubber trees in Bangladesh plantations are not well understood. As a result, there is a need for growth and yield tables for this species to ensure effective plantation management. The available growth data for the species is insufficient and cannot be used to create an age-growth equation. Consequently, this study was conducted to gather scientific data for predicting the growth and yield of rubber trees based on site indices.

Rubber tree, were planted in Chittagong, Cox’s Bazar, Chittagong Hill-tracts, Sylhet and Tangail at different time under development programmed of BFIDC and Private Rubber Planter. The Sample plots to be establish in these areas. Data have been collected the following rubber garden (Figure 1) through the establishment of temporary sample plots (Table 1).

Figure 1 Map of the study area.

Sample plots and data for growth models

Temporary sample plots (TSP) were established in the available plantations within the study areas. These plots were either square or rectangular, each covering an area of 0.02 hectare. The diameter at breast height (Dbh), total height, and spacing of all trees in the plots were measured. In total, 362 sample plots (Table 2) were set up in the studied plantations. Dbh and height of all trees in the plots were measured using diameter tapes and a Haga altimeter, respectively. Plantations with the largest age ranges were selected for the study, and at least five plots were randomly chosen from each plantation. The heights of the two tallest trees (100 trees per hectare) in each plot were recorded using a height measuring instrument to determine the dominant height. The Dbh and height data of all trees in the plots were entered into a computer for analysis.

Tree measurements

1. Diameter at breast height (Dbh) in centimeter using a diameter tape
2. Total height (ht) in meter using Haga altimeter
3. Age in years taken from the records of the owner/office

Data collation

For statistical analysis, data were obtained for the mean stand Dbh, mean dominant height (H), mean stand height (Mht), basal area per hectare (Baha^-1), total volume per hectare (Vtha^-1), total biomass per hectare (Biomha^-1), and site index. The average number of stems per hectare (Nha^-1) in each age group was also calculated. The volume of each tree was estimated using the volume equation for the species developed by Islam et al.,¹² as follows: R² = 0.97 and RSE = 0.15

The biomass of the individual tree was estimated by using the biomass allometric model for the species developed by Mahmood et al.¹³ of the form:

In( TAGB )=0.738+0.890×In( D )+0.746×In( H ); MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqkY=MjYdH8pE0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaq pepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=x b9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamysaiaad6gada qadaqaaiaadsfacaWGbbGaam4raiaadkeaaiaawIcacaGLPaaacqGH 9aqpcaaIWaGaaiOlaiaaiEdacaaIZaGaaGioaiabgUcaRiaaicdaca GGUaGaaGioaiaaiMdacaaIWaGaey41aqRaaiysaiaac6gadaqadaqa aiaadseaaiaawIcacaGLPaaacqGHRaWkcaaIWaGaaiOlaiaaiEdaca aI0aGaaGOnaiabgEna0kaadMeacaWGUbWaaeWaaeaacaWGibaacaGL OaGaayzkaaGaai4oaaaa@584B@ R² = 0.937 and RSE = 0.147

We derived information on stand height, dominant height, stand height, stand basal area per hectare, stand volume per hectare and stand basal area per hectare. The models represented in Table 3 were tested for the selection of the best-suited site index guide model.

Among the models mentioned above, the most appropriate ones were selected based on their ability to meet both statistical and biological criteria. The development of Site Index Curves (SIC) for the studied tree species followed the "difference equation method" outlined by Clutter et al.¹⁴

For the determination of the best-suited growth and yield models, the site index guide equation was developed first. This was followed by the derivation of stand mean diameter at breast height (Dbh), stand mean height (Mht), stand basal area ha^-1 (Ba ha^-1), stand volume ha^-1 (V_t ha^-1) and stand above ground biomass ha^-1 (Biom ha^-1) yield models. The independent variables of the stand yield prediction models were age and site index and the dependent variable was Dbh, Mht, Ba ha^-1, V_t ha^-1 and Biom ha^-1. One model to estimate the number of trees per hectare at different ages were also derived. Step-wise and all probable combinations of the independent variables regression methods were used to select the best-suited models subject to the satisfaction of the statistical and biological requirements. Different transformations of the variables either in the form of natural logarithm (ln), reciprocal or combining two variables in the transformed or the original forms or combinations along with the original variables were used for regression analyses. All possible regressions were worked out by taking ln as dependent variable. Independent variables in the form of 1/ S, ln(S), 1/ ln(S) for site index and 1/A, ln(A) and S/A for age were used. Two-stage least squares method was used to choose desired equation out of the different combinations. In this way, equations for stand mean height, stand Dbh, stand basal area ha^-1, stand volume ha^-1 and stand biomass ha^-1 were derived. The stand variables presented in the Table 4.

To determine the most suitable growth and yield models, the site index guide equation was developed first. This was followed by the creation of yield models for stand mean diameter at breast height (Dbh), stand mean height (Mht), stand basal area per hectare (Baha^-1), stand volume per hectare (Vtha^-1), and stand above-ground biomass per hectare (Biomha^-1). The independent variables for the stand yield prediction models were age and site index, while the dependent variables were Dbh, Mht, Baha^-1, Vtha^-1, and Biomha^-1. A model to estimate the number of trees per hectare at various ages was also developed. Stepwise regression and all possible combinations of independent variables were used to select the best models, ensuring they met both statistical and biological criteria. Various transformations of the variables, such as natural logarithms (ln), reciprocals, or combinations of transformed and original variables, were applied for regression analysis. All possible regressions were calculated with ln as the dependent variable. Independent variables for site index included 1/S, ln(S), and 1/ln(S), while those for age included 1/A, ln(A), and S/A. The two-stage least squares method was used to select the preferred equation from the various combinations. In this manner, equations for stand mean height, DBH, basal area per hectare, volume per hectare, and biomass per hectare were derived, with the results presented in Table 4.

Fixing rotation age using Mean Annual Increment (MAI) and Current Annual Increment (CAI) curves involves plotting and analyzing these growth curves for forest tree species. There is a mathematical theorem that states that “The maximum yield attains at that point where the MAI curve and CIA curve meet”. To fixation rotation age using this theorem.

Model performance criteria

Choosing the right criteria to evaluate model performance is a crucial factor. There is no universal criterion for selecting the best regression model from several options.¹⁵ A more objective and common approach is to use multiple performance measurements rather than relying on a single one.¹⁵

The coefficient of determination (R²) is one of the most commonly used criteria for evaluating model performance. The R² statistic assesses how well the regression predicts the values of the dependent variable within the sample. In standard interpretations, it represents the proportion of the variance in the dependent variable explained by the independent variables. If the regression fits perfectly, the R² value will be very close to one. The R² is calculated as:

The root mean square error (RMSE) is a widely recognized measure of goodness-of-fit that quantifies the difference between observed and predicted values, expressed in the relevant units, with a lower value indicating a better fit.¹⁵ RMSE is defined as follows:

where, and  are the original data values and modeled (predicted) values respectively and mean of original data. N is the number of pairs of values.

The Akaike Information Criterion (AIC) is regarded as one of the most dependable criteria for comparing models with different parameters.^13,15 The model with the lowest AIC is considered the best. For the least squares fit, it is calculated as follows:¹⁵

AIC = -2(log-likelihood) + 2K

Where, K is the number of model parameters (the number of variables in the model plus the intercept). Log-likelihood is a measure of model fit. The higher the number, the better the fit. This is usually obtained from statistical output.

Model validation

Statistical validation

Statistical validation was the first step in validating the models. It included the analysis of variance minimum residual mean square, the highest coefficient of determination (R²) and the highest adjusted R² with the lowest RMSE.

Independent test

Validation of the chosen models of stand variables for rubber trees was done by using data from 30 separate sample plots. This was done by comparing the estimated and observed values, applying the chi-square test of goodness of fit, paired t-test and percent absolute deviation (%AD). This was also compared with the 45-degree line test by plotting the observed values and the predicted value in the graph.

Biological principle testing

To test the biological principles, the predicted stand mean height, stand Dbh, stand basal area per hectare, total volume yield per hectare, and above-ground biomass yield per hectare, derived from the selected models, were plotted against age for different site indices. The yield curves should exhibit a sigmoid shape and approach the site’s carrying capacity asymptotically.^6,8,9

The collected data represented in table 2, is categorized in nine age group such as 1976-1980; 1981-1985; 1986-1990; 1991-1995; 1996-2000; 2001-2005; 2006-2010; 2011-2015 and 2016-2020. The growth data shows that the tree species among the ten age groups is statistically normally distributed (Figure 2), which is crucial for developing accurate growth and yield models.

Figure 2 Sample plot distribution among the age group.

Development of site index guide equation

The growth and yield prediction models for the species were developed using the site index guide equation method. The mean dominant height was measured from a total of 362 individual temporary sample plots (Table 1 and Figure 2) in this study. Figure 3 presents scatter plots showing the relationship between the mean dominant height and the age of rubber trees (Hevea brasiliensis Muell. Arg.) grown in plantations in Bangladesh. The scatter plot also illustrates the relationship between the dependent variable (dominant height) and the independent variable (age) using the actual field data before model fitting. The figure shows that dominant height increases monotonically with the tree’s age, indicating a strong correlation between the dependent and independent variables.

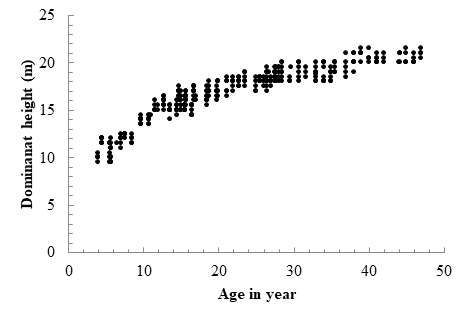
Figure 3 The scatter plot of the individual means dominant height with independent variable age of rubber tree (Hevea brasiliensis. Muell Arg.)

Schumacher’s model to develop a site index guide equation was found best suited for rubber tree (Hevea brasiliensis. Muell Arg.) grown in the plantations in Bangladesh. The results of model performance criteria are shown in Table 5. The specific form of the equation is given by:

The coefficient of determination (R²=0.92) of the selected site index model explains about 92% of the total variations. The site index guide curve is given in Figure 4.

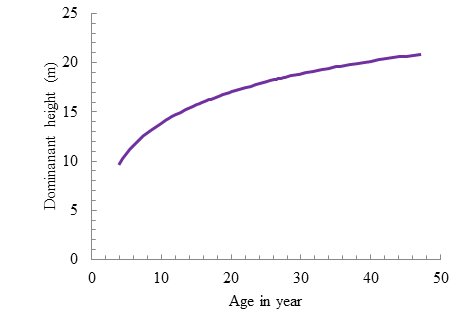
Figure 4 Site index guide equation for rubber tree (Hevea brasiliensis. Muell Arg.) plantations in Bangladesh.

To obtain the site index for each plot, a reference age or base age (closed to rotation age) of 25 years was used and the specific equation is given as flows:

Where, S is the site index of an individual plot at a base age of 25 years.

For a given age and dominant height, the site index can also be derived from the graphical representation of the site index curves fitted for the Schumacher model guide curve at an index age of 25 years (Figure 5). The selected models satisfied all the above-mentioned statistical criteria. The predicted values were plotted against age for different site indices. The growth curves were sigmoid. The growth curves also showed that at a given stand age, higher growth is expected on better sites (Figure 4). The selected stem per hectare prediction equation, stand mean height equation, stand diameter at breast height growth equation, stand density or stand basal area in square meters per hectare prediction equation, stand volume cubic meters per hectare prediction equations and biomass ton per hectare prediction equations are stated in Table 6 below along with the corresponding coefficient of determination and root square mean error.

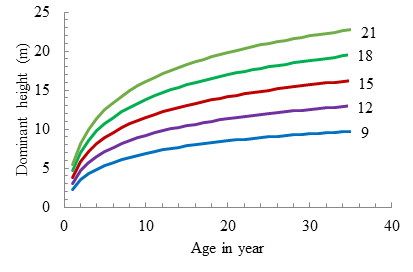
Figure 5 Site index curves of fitted by the Schumacher guide curve at index age of 25 years for rubber tree (Hevea brasiliensis. Muell Arg.) plantations in Bangladesh.

Statistical validation and biological principle testing

The selected models satisfied all the statistical criteria. The predicted values were plotted against ages for different site indices (Figure 2). The curves found to confirm with the ideal attributes of a biological yield curves. The yield curves were sigmoid in this tree species. The yield curves also showed that at a given stand age, higher yield is expected on better sites.

Independent test

The computed chi-square, t-value, absolute deviation present (%AD) and slope for the number of trees ha^-1, mean height, diameter at breast height, basal area ha^-1, volume ha^-1 and biomass ha^-1 are given in Table 7.

The computed chi-square and t-values were less than the tabular values χ 0.95,29 2 =17.71 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqkY=MjYdH8pE0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaq pepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=x b9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeq4Xdm2aa0baaS qaaiaaicdacaGGUaGaaGyoaiaaiwdacaGGSaGaaGOmaiaaiMdaaeaa caaIYaaaaOGaeyypa0JaaGymaiaaiEdacaGGUaGaaG4naiaaigdaaa a@4365@ and t 0.95,29 =2.045 MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqkY=MjYdH8pE0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaq pepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=x b9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiDamaaBaaale aacaaIWaGaaiOlaiaaiMdacaaI1aGaaiilaiaaikdacaaI5aaabeaa kiabg2da9iaaikdacaGGUaGaaGimaiaaisdacaaI1aaaaa@41E5@ . These imply that there is no significant difference between the actual values from the 30 test sample plots and the corresponding expected values as predicted by the models. Hence, the selected models confirm the set of data.

45 degree line test

Graphs comparing the observed values and the predicted values were plotted in the graph paper. It was observed that the models tend to make an angle of 45 degree with the axes meaning there is no significant difference between actual and predicted values.

Fixation of rotation age of rubber tree

The predicted growth equation for the total volume of the rubber tree (Hevea brasiliensis. Muell Arg.) in this study was the logarithm equation and, thus, this could be used for volume extrapolations. Rotation ages and expected total volumes to be yielded were calculated from this growth equation. Using the volume prediction model for the average site (SI 15 meter) the mean annual increment (MAI) curve and current annual increment (CAI) are represented in the figure. The rotation age of H. brasiliensi had to be estimated visually from its growth curve (Figure 6).

Figure 6 Current annual increment (CAI) of stand volume at different forest stand ages, mean annual increment (MAI) since stand establishment for rubber tree.

Estimated parameters and fit statistics of fitted models are presented in Table 5. The four models represented in Table 3 were tested to develop a site index guide equation of the rubber tree. Three models had two, one model had three estimated parameters. The standard errors given in the table show that all the partial regression coefficients were statistically level of significant at 0.01%.

The performance measures for four generalized height growth functions using the calibration dataset are summarized in Table 4. Significant differences were observed in the predictive abilities of the generalized dominant height-age models. Models with the lowest RSE and AIC values (closer to zero) and an R² value closest to unity demonstrated the best performance.¹⁶ Positive serial correlation was found in all models, as indicated by the Durbin-Watson statistic values ranging between 0 and 2. The highest R² was achieved by the Schumacher model (0.92) and the Power model (0.91), followed by the Chapman-Richards model (0.81) and the Lars Strand model (0.79).

Model statistics indicated that the Schumacher and Chapman-Richards models fitted the tree dominant height-age data of rubber trees almost equally well. The Schumacher model explained at least 92% of the total variation in tree-dominant heights. It also had a smaller RSE (0.05) compared to the other model for the studied species. Additionally, the generalized dominant height-age function of the Schumacher model produced the lowest AIC value (-3.03), which is closer to zero than the other models.

In the literature, these four nonlinear growth functions are commonly chosen as suitable candidate models for the dominant height-age relationship of rubber trees (Hevea brasiliensis Muell. Arg.) grown in plantations in Bangladesh. The models not only possess appropriate mathematical and statistical characteristics but also offer the potential for biological interpretation of the parameters related to tree-dominant height-age relationships (Fang and Bailey, 1998; Latif, 1999). In this study, the predicted models were plotted against the observed values concerning age, and the results indicate that all the models exhibit a sigmoid shape.

The regression coefficients for the predicted models of stand stocking, stand mean height, stand diameter at breast height, stand basal area per hectare, stand volume yield per hectare, and stand biomass yield per hectare are highly significant, with values of 0.87, 0.95, 0.94, 0.91, 0.93, and 0.90, respectively (Table 5). These values demonstrate a strong correlation between the predicted stems per hectare and the independent variable age (A). Furthermore, stand mean height, stand diameter at breast height, stand basal area per hectare, stand volume yield per hectare, and stand biomass yield per hectare are all strongly correlated with both age (A) and site index (SI). This indicates that the models for stand stocking, stand mean height, stand diameter at breast height, stand basal area, stand volume, and stand biomass yield explain 87%, 95%, 94%, 91%, 93%, and 90% of the total variation, respectively, at a significant level of P<0.01. The standard errors for the number of stems per hectare (5), stand mean height per tree (0.05 meters), DBH per tree (0.09 centimeters), stand basal area per hectare (0.19 square meters), stand volume yield per hectare (0.20 cubic meters), and stand biomass yield per hectare (0.12 tons) were relatively low, suggesting a good model fit. The predicted curves are shown in Figure 7.

Figure 7 Predicted growth and yield curves of rubber tree plantations in Bangladesh.

The analyses in this study revealed a broad range of impacts that different rotation lengths have on various ecosystem services and biodiversity conservation. In terms of wood production, both shortening and extending rotations would reduce economic outputs compared to current practices (assuming no significant forest damage). However, these two strategies may have differing effects on harvesting logistics and the supply of specific wood products. Shortening rotations is expected to have mostly negative or neutral effects on other provisioning services while extending rotations is likely to have positive or uncertain impacts on these services.

Wood volume growth in managed even-aged stands follows a pattern where the Current Annual Increment (CAI) increases after stand establishment, peaks when the maximum leaf area is reached, and then declines (Figure 6). The shapes of the CAI and the resulting Mean Annual Increment (MAI) curves (i.e., average annual increment since stand establishment) vary depending on tree species and site conditions. These two curves intersect at the point where the MAI reaches its maximum, which is considered the optimal time for harvesting to maximize wood volume production. For rubber trees, the rotation age for maximum wood production is estimated to be around 27 years on average in sites with an SI of 15 m, as growth significantly declines after this age. The rubber tree growth curve remains useful for interpolation in applications.

This study provides detailed growth and yield models for rubber tree (Hevea brasiliensis Muell Arg.) plantations in Bangladesh. The models are based on six key equations: stand stocking, stand mean height, stand diameter growth, stand density, stand volume yield, and stand biomass yield. These equations predict various parameters, including the number of trees per hectare (stocking), stand mean height, dominant height, diameter at breast height, basal area (density) per hectare, and volume and biomass per hectare at different sites. Forest users can easily access values from the tables derived from these models, eliminating the need for manual calculations. By knowing the age and site indices of a rubber tree stand, users can accurately and safely estimate growth and yield variables using the models provided in this study.

The author believes that sample plots covering a range of site variations and stand histories are essential for developing a standard model for a given forest type or plantation species. However, this study was unable to achieve that due to time constraints and other limiting factors. Developing growth and yield models through Permanent Sample Plots requires more than ten years of continuous data. Additionally, rubber tree (Hevea brasiliensis Muell Arg.) plantations are so widely dispersed across the country that it was impossible to include a balanced representation of poor, average, and good sites, as well as old logged stands, mid-rotation stands, and stands at the end of the felling cycle, all of which are necessary for an ideal model. Furthermore, no conventional thinning was carried out in the plantations studied, leading to some irregularities in the data analysis. The models could be improved by incorporating data from a broader range of stocking variations (number of stems per unit area) to refine the estimation of independent variables.

This study developed growth and yield models for rubber trees (Hevea brasiliensis Muell Arg.) planted in Bangladesh using a site index guide equation. All of the models play a crucial role in enhancing our understanding of rubber tree growth in Bangladesh.

The main goal of this research was to evaluate the growth and yield of rubber trees (Hevea brasiliensis Muell Arg.) using various suitable methods, to apply these findings to growth and yield simulators and the fundamental calculations involved in forest inventories in Bangladesh. To achieve this, the model utilized predictors typically collected during forest inventories. The data gathered during fieldwork was found to be appropriate for developing these models. In this study, the total volume of rubber trees was predicted using a model by Islam et al.,¹⁷ while biomass was estimated using a model by Mahmood et al.,¹³ which served as the reference for individual tree volume and biomass. The research focused on developing growth and yield prediction models to support the sustainable management of rubber plantations in Bangladesh. Both statistical and biological evaluations of these models indicated reasonable prediction accuracy. Additionally, the models performed well when applied to independent test data and were consistent with established forest growth theories. In the context of Bangladesh, these growth models can be valuable for forest planning, helping assess site quality and estimate stand yield at specific times.

The selected growth and yield models can be effectively used within the constraints of the available data and study area. These models are applicable for ages ranging from 4 to 45 years and site indices between 9 and 21 meters. However, the models should not be applied to a single plot. A sufficient number of plots should be collected first, and then average parameters can be used to forecast growth and yield. To convert linear measurements, divide the value by 2.54 to convert centimeters to inches. To convert height from meters to feet, multiply the value by 3.281. Similarly, to convert the area from square meters to square feet, multiply by 10.76, and to convert volume from cubic meters to cubic feet, multiply by 35.32.^18–20

None.

The author declares there is no conflict of interest.

1. Spurr SH. Forest Inventory. Ronald Press, New York. 1952. p. 476.
2. Minor CO. Principles of growth and yield. In 31st annual forestry symposium; Predicting growth and yield in mid-south. In: EJ Hot, et al., editors. Baton Rouge, Division of continuing education Louisiana State Univ. 1982. p. 1–10.
3. Vanclay JK. Modelling forest growth and yield. Applications to mixed tropical forests. CAB International, Oxon, U.K., 1994. p. 312.
4. Vanclay JK, Skovsgaard JP. Evaluating forest growth models. Ecol Modell. 1997;98(1):1–12.
5. Latif MA, Das S, Rahman MF, et al. Growth and yield tables for Acacia mangium grown in the plantations in Bangladesh. Journal of Tropical Forest Science. 1995;7(4):591–598.
6. Latif MA, Chowdhury JA, Das S, et al. Growth and yield models for gamar (Gmelina arborea) the plantations of Bangladesh. Bangladesh Journal of Forest Science. 1997;24 (1):7–12.
7. Avery TE, Burkhart HE. Forest measurements, 5th McGraw Hill, New York. 2002. 456 p.
8. Islam SMZ, Chowdhury MA, Misbahuzzaman K. Mathematical Models for Estimating Tree Site Index for Agar tree (Aquilaria malaccensis Lamk) Plantations in Bangladesh. Indian Forester. 2018;144(12):1172–1178.
9. Islam SMZ, Khan MI, Azad. Growth and Yield Prediction Models for Acacia auriculiformis (Akashmoni) Grown in the Plantations of Bangladesh. Medicon Agriculture & Environmental Sciences. 2023;5(3):04–15.
10. Latif MA, Del Castillo RA. Rotation ages of keora (Sonneratia apetala Buch-Ham) inthe coastal plantations in Bangladesh. Bangladesh Journal of Forest Science. 1991;20(1&2):1–7.
11. Ali M. Bangladeshi Rubber Gaser Autit, Bartaman abong Bhabiswat (in Bangla). Rubber Bichitra. Yearly Journal of BFIDC. 73, Motijheel Commercial Area, Dhaka. 1985. p. 1–3.
12. Islam SMZ, Khan MI, Ahmed KU. Mathematical Volume equation and Table of Rubber tree, (Hevea brasiliensis. Muell Arg.), Bulletin No. 10. Forest Inventory Division. Bangladesh Forest Research Institute, P. O. Box-273, Chittagong - 4000, Bangladesh. 2014. p. 24.
13. Mahmood H, Saha C, Siddique MRH, et al. Development of allometric biomass models for Hevea brasiliensis Müll. Arg. plantation of Bangladesh: a non-destructive approach. Indian Forester. 2021;147(4):366–373.
14. Clutter JL, Fortson JC, Pienaar LV, et al. Timber management: A quantitative approach. John Wiley & Sons, USA. 1983. 333 p.
15. Aertsen W, Kint V, Van Orshoven J, et al. Comparison and ranking of different modeling techniques for prediction of site index in Mediterranean mountain forests. Ecological Modelling. 2010;221(8):1119–1130.
16. Ahmadi K, Alavi SJ. Generalized height diameter models for Fagus orientalis Lipsky in Hyrcanian forest, Iran. J FOR SCI. 2006;62(9):413–421.
17. Latif MA, Islam SMZ. Growth, Yield, Volume and Biomass Equation and Tables for Important Trees in Bangladesh. Forest Inventory Division. Bangladesh Forest Research Institute, P. O. Box-273, Chittagong - 4000, Bangladesh. 2014. p. 106.
18. Revised Project Proposal for Second Rubber Development Project, Tangail and Sherpur Region, Planning and Development Division, Government of the Peoples’ Republic of Bangladesh. 1995. 131 p.
19. Sharma RP. Modelling height-diameter relationship for Chir pine trees. Banko Janakari. 2009;19:3–9.
20. Tissari J. Further development of the rubber wood processing industries in producer countries. Proceedings on Fifth Joint Workshop of the Secretariat of the United Nations Conference on Trade and Development and the International Rubber Study Group on Rubber and the Environment, February 5, 2002. Glasgow, UK. 2002. p. 34–78.