Schemes nano piezo engine for applied bionics

doi:10.15406/mojabb.2025.09.00222

MOJ

eISSN: 2576-4519

Applied Bionics and Biomechanics

Research Article Volume 9 Issue 1

Schemes nano piezo engine for applied bionics

Afonin SM

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

National Research University of Electronic Technology, Russia

Correspondence: Afonin SM, National Research University of Electronic Technology, MIET, 124498, Moscow, Russia

Received: April 17, 2025 | Published: May 1, 2025

Citation: Afonin SM. Schemes nano piezo engine for applied bionics. MOJ App Bio Biomech. 2025;9(1):35-38. DOI: 10.15406/mojabb.2025.09.00222

Download PDF

Abstract

The schemes with lumped parameters and distributed parameters of the nano piezo engine are constructed for applied bionics. The scheme of the nano piezo engine is founded by method mathematical physics. The displacement matrix of nano engine is determined.

Keywords: nano piezo engine, scheme, applied bionics

Introduction

The nano piezo engine is used in applied bionics for nano positioning system, dampen mechanical vibrations, adaptive optics, ring quantum generator, scanning microscopy, works with DNA.^1–18 Its scheme is constructed by method mathematical physics for lumped parameters or distributed parameters of nano piezo engine.

Schemes

Let us consider the scheme of the nano piezo engine for lumped parameters. The scheme of nano piezo engine is determined by method mathematical physics with using the equation of the reverse piezo effect and the equations forces of engine in dynamics.^16–57

The equation of the reverse piezo effect has the form^3–59

S_{i} = d_{m i} E_{m} + s_{i j}^{E} T_{j}

here the indexes i, j, m and $S_{i}, E_{m}, T_{j}, d_{m i}, s_{i j}^{E}$ are the relative displacement, the strength electric field, the strength mechanical field, the piezo module, and the elastic compliance at $E = const .$

Than the Laplace transform general force $F (s)$ of the nano piezo engine is founded

F (s) = d_{m i} S_{0} E_{m} (s) / s_{i j}^{E}

We have the transform general force by using the voltage $U_{C} (s) = U (s) / (R C_{0} s + 1)$ on the piezo capacitor in the form

F (s) = \frac{d_{m i} S_{0} U_{C} (s)}{δ s_{i j}^{E}} = \frac{d_{m i} S_{0} U (s)}{δ s_{i j}^{E} (R C_{0} s + 1)}

The Laplace transform general force of the nano piezo engine is written

F (s) = k_{r} U_{C} (s)

here $k_{r}$ is the reverse coefficient in the form

k_{r} = \frac{d_{m i} S_{0}}{δ s_{i j}^{E}}

The equation direct piezo effect has form^3–43

D_{m} = d_{m i} T_{i} + ε_{m k}^{E} E_{k}

here $ε_{m k}^{E}$ is the permittivity.

Than the direct coefficient $k_{d}$ is founded in the form

k_{d} = k_{r} = \frac{d_{m i} S_{0}}{δ s_{i j}^{E}}

The Laplace transform voltage for the first feedback on the velocity of the second end is founded on Figure 1 in the form

U_{d} (s) = \frac{d_{m i} S_{0}}{δ s_{i j}^{E}} {\dot{Ξ}}_{2} (s) R = k_{d} {\dot{Ξ}}_{2} (s) R

by using the Laplace transform velocity the second end ${\dot{Ξ}}_{2}$ of the nano engine.

The transform force at the second end $F_{2} (s)$ and the load force $F_{l} (s)$ are subtracted on Figure 1. The Laplace transform force for the second feedback has the form

F_{l} (s) = (C_{e} + C_{i j}^{E} + k_{ν} s) Ξ_{2} (s)

here $C_{e}, C_{i j}^{E}, k_{ν}$ are the elastic load stiffness, the stiffness piezo engine, the coefficient of viscous friction. This Laplace transform the load force has form the sum of the elastic force and the viscous friction force.

The scheme for lumped parameters of the nano piezo engine is constructed on Figure 1 at the first fixed end, the elastic inertial load with the mass load $M_{2}$ and the voltage control.

The transfer function for lumped parameters of the nano engine on Figure 1 has the form

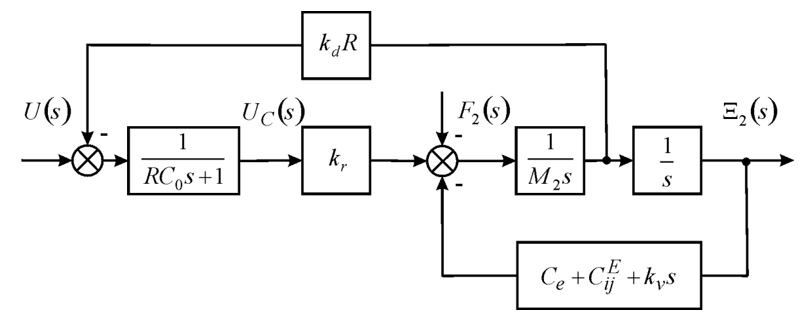
Figure 1 Scheme for lumped parameters nano engine.

W (s) = Ξ_{2} (s) / U (s) = k_{r} / (a_{3} p^{3} + a_{2} p^{2} + a_{1} p + a_{0})

$a_{3} = R C_{0} M_{2}$ , $a_{2} = M_{2} + R C_{0} k_{v}$

$a_{1} = k_{v} + R C_{0} C_{i j}^{E} + R C_{0} C {}_{e}+ R k_{r} k_{d}$ , $a_{0} = C {}_{e}+ C_{i j}^{E}$

At $R = 0$ the transfer function is founded in the form

W (s) = Ξ_{2} (s) / U (s) = k_{31}^{U} / (T_{t}^{2} s^{2} + 2 T_{t} ξ_{t} s + 1)

k_{31}^{U} = d_{31} (h / δ) / (1 + C_{e} / C_{11}^{E})

$T_{t} = \sqrt{M_{2} / (C_{e} + C_{11}^{E})}$ , $ω_{t} = 1 / T_{t}$

At nano PZT engine $M_{2}$ = 1 kg, $C_{e}$ = 0.4×10⁷ N/m, $C_{11}^{E}$ = 1.2×10⁷ N/m its parameters are determined $T_{t}$ = 0.25×10^-3 s, $ω_{t}$ = 4×10³ s^-1.

At PZT drive $d_{31}$ = 0.2∙nm/V, $h / δ$ = 20, $C_{e} / C_{11}^{E}$ = 0.33 its transfer coefficient is founded $k_{31}^{U}$ = 3 nm/V.

Let us consider the scheme in general of the nano piezo engine for distributed parameters.

The scheme of nano engine is constructed by method mathematical physics with the equation of the reverse piezo effect and the equations forces in dynamics at the boundary conditions the differential equation of engine.

The ordinary differential equation of the nano piezo engine has form^8–49

\frac{d^{2} Ξ (x, s)}{d x^{2}} - γ^{2} Ξ (x, s) = 0

here $Ξ (x, s)$ , $x$ , s, $γ$ are the Laplace transform displacement, the coordinate, the parameter, the propagation coefficient and the general length $l = {h, δ, b$ the nano piezo engine, For the nano piezo engine at $x = 0,$ $Ξ (0, s) = Ξ_{1} (s)$ and at $x = l$ , $Ξ (l, s) = Ξ_{2} (s) .$

The solution of the ordinary differential equation has the form

Ξ (x, s) = {Ξ_{1} (s) sh [(l - x) γ] + Ξ_{2} (s) sh (x γ)} / sh (l γ)

and the boundary conditions are determined

T_{j} (0, s) = \frac{1}{s_{i j}^{Ψ}} {\frac{d Ξ (x, s)}{d x} |}_{x = 0} - \frac{ν_{m i}}{s_{i j}^{Ψ}} Ψ_{m} (s)

T_{j} (l, s) = \frac{1}{s_{i j}^{Ψ}} {\frac{d Ξ (x, s)}{d x} |}_{x = l} - \frac{ν_{m i}}{s_{i j}^{Ψ}} Ψ_{m} (s)

The Laplace transform of the general force of the nano piezo engine has the form

F (s) = ν_{m i} Ψ_{m} (s) / χ_{i j}^{Ψ}

here $χ_{i j}^{Ψ} = s_{i j}^{Ψ} / S_{0} .$

The general scheme and model for distributed parameters of the engine on Figure 2 are determined at voltage or current control

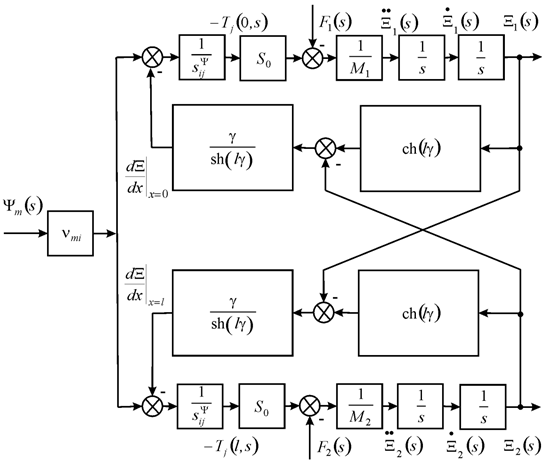
Figure 2 General scheme for distributed parameters nano piezo engine.

Ξ_{1} (s) = {(M_{1} s^{2})}^{- 1} {\begin{cases} - F_{1} (s) + {(χ_{i j}^{Ψ})}^{- 1} \\ \times [\begin{array}{l} ν_{m i} Ψ_{m} (s) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{1} (s) - Ξ_{2} (s)] \end{array}] \end{cases}}

Ξ_{2} (s) = {(M_{2} s^{2})}^{- 1} {\begin{cases} - F_{2} (s) + {(χ_{i j}^{Ψ})}^{- 1} \\ \times [\begin{array}{l} ν_{m i} Ψ_{m} (s) - [γ / sh (l γ)] \\ \times [ch (l γ) Ξ_{2} (s) - Ξ_{1} (s)] \end{array}] \end{cases}}

here $v_{m i} = {\begin{matrix} d_{33}, d_{31}, d_{15} \\ g_{33}, g_{31}, g_{15} \end{matrix}$ , $Ψ_{m} = {\begin{matrix} E_{3}, E_{3}, E_{1} \\ D_{3}, D_{3}, D_{1} \end{matrix}$

$s_{i j}^{Ψ} = {\begin{matrix} s_{33}^{E}, s_{11}^{E}, s_{55}^{E} \\ s_{33}^{D}, s_{11}^{D}, s_{55}^{D} \end{matrix}$ , $γ = {γ^{E}, γ^{D}$ , $c^{Ψ} = {c^{E}, c^{D}$

The general scheme for distributed parameters of the nano engine on Figure 2 is used in applied bionics and biomechanics.

The displacement matrix has the form

(\begin{matrix} Ξ_{1} (s) \\ Ξ_{2} (s) \end{matrix}) = (W (s)) (\begin{matrix} Ψ_{m} (s) \\ F_{1} (s) \\ F_{2} (s) \end{matrix})

(W (s)) = (\begin{matrix} \begin{matrix} W_{11} (s) & W_{12} (s) & W_{13} (s) \end{matrix} \\ \begin{matrix} W_{21} (s) & W_{22} (s) & W_{23} (s) \end{matrix} \end{matrix})

with the transfer functions in the form

W_{11} (s) = Ξ_{1} (s) / Ψ_{m} (s) = {ν_{m i} [M_{2} χ_{i j}^{Ψ} s^{2} + γ th (l γ / 2)] / A}_{i j}

W_{12} (s) = Ξ_{1} (s) / F_{1} (s) = - {χ_{i j}^{Ψ} [M_{2} χ_{i j}^{Ψ} s^{2} + γ / th (l γ)] / A}_{i j}

W_{13} (s) = Ξ_{1} (s) / F_{2} (s) = W_{22} (s) = Ξ_{2} (s) / F_{1} (s) = {[χ_{i j}^{Ψ} γ / sh (l γ)] / A}_{i j}

W_{23} (s) = Ξ_{2} (s) / F_{2} (s) = - {χ_{i j}^{Ψ} [M_{1} χ_{i j}^{Ψ} s^{2} + γ / th (l γ)] / A}_{i j}

here $\begin{array}{l} A_{i j} = M_{1} M_{2} {(χ_{i j}^{Ψ})}^{2} s^{4} + {(M_{1} + M_{2}) χ_{i j}^{Ψ} / [c^{Ψ} th (l γ)]} s^{3} + \\ + [(M_{1} + M_{2}) χ_{i j}^{Ψ} α / th (l γ) + 1 / {(c^{Ψ})}^{2}] s^{2} + 2 α s / c^{Ψ} + α^{2} \end{array}$

The static displacements of the transverse engine are determined

ξ_{1} = d_{31} (h / δ) U M_{2} / (M_{1} + M_{2})

ξ_{2} = d_{31} (h / δ) U M_{1} / (M_{1} + M_{2})

At the transverse PZT engine $M_{1}$ = 0.25 kg, $M_{2}$ = 1 kg, $d_{31}$ = 0.2 nm/V, $h / δ$ = 10, $U$ = 150 V the static displacements are founded $ξ_{1} + ξ_{2}$ = 300 nm and $ξ_{1}$ = 240 nm, $ξ_{2}$ = 40 nm.

Discussion

The nano piezo engine is used in applied bionics for scanning microscopy and adaptive optics. The structural scheme of the nano engine is determined. For the nano piezo engine the displacement matrix is constructed. The general schemes for engine are founded.

Conclusion

The schemes for lumped parameters and distributed parameters of the nano engine and its transfer functions are constructed by method mathematical physics. The displacement matrix and the transfer functions are determined for applied bionics.