
Research Article Volume 2 Issue 2
Noise cancellation from vibrocardiographic signals based on the ensemble empirical mode decomposition
Taebi A,
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Mansy HA
University of Central Florida, USA
Correspondence: Amirtaha Taebi, PhD Student, 1Biomedical Acoustics Research Laboratory, University of Central Florida, 4000 Central Florida Blvd., Orlando, FL 32816, USA, Tel 1 (407) 580-4654
Received: October 31, 2016 | Published: February 10, 2017
Citation: Taebi A, Mansy HA. Noise cancellation from vibrocardiographic signals based on the ensemble empirical mode decomposition. J Appl Biotechnol Bioeng. 2017;2(2):49-54. DOI: 10.15406/jabb.2017.02.00024
Download PDF
Abstract
Vibrocardiographic (VCG) signals are the cardiac vibration measured at the chest surface. These signals can contain useful information for diagnosing cardiac conditions but are often contaminated by noise. Although band-pass and adaptive filters were used for noise removal from similar signals, the utility of ensemble empirical mode decomposition (EEMD) for filtering VCG was not previously investigated. In this study, an EEMD-based filter was proposed and tested. The filtering scheme first decomposed the VCG waveform into a set of intrinsic mode functions (IMF) then utilized the partial sum of IMFs to remove white noise that was added to simulated VCG signals. To measure the filter effectiveness, the normalized root-mean-square error (NRMSE) between the clean (i.e., before adding noise) and filtered signals was calculated for signal-to-noise ratios ranging from 1 to 20dB. The EEMD-based filter performance was also compared with traditional methods such as Wiener filter. This comparison suggested that EEMD-based filter outperformed the Wiener filter in noise removal from simulated VCG. These results also suggested that EEMD may be utilized for white noise removal from actual VCG signals. Further investigations are warranted to study the relation between IMFs and different types of noise, which can enhance the effectiveness of EEMD-based filters in removing these noise types from actual VCG signals.
Keywords: noise cancellation, wiener filter, priori, denoising, cardiotocography, misadjustment
Abbreviations
VCG, vibrocardiographic; EEMD, ensemble empirical mode decomposition; IMF, intrinsic mode functions; NRMSE, normalized root-mean-square error; SNR, signal-to-noise ratio
Introduction
Empirical mode decomposition (EMD) is a signal processing technique proposed for the analysis of non-stationary and nonlinear signals.1 EMD has been successfully applied to solve numerous practical problems in various applications.2-9 This technique decomposes a time series into a set of zero-mean underlying components called intrinsic mode functions (IMF). The main advantage of EMD is that it is an adaptive method. For example, the EMD algorithm depends only on the signal under analysis and does not require any a priori defined basis system. One of the main drawbacks of EMD is mode mixing that occurs when either signal of a similar scale resides in more than one IMF or an IMF consists of signals of broadly different scales.10 This issue may cause some IMFs to become physically meaningless. Ensemble EMD (EEMD) was developed to overcome the EMD mode mixing issue. 10 The improved algorithm, EEMD, is based on one of the most important properties of EMD, namely that EMD behaves as a dyadic filter bank when applied to white Gaussian noise.11,12 The principle of EEMD is to add a finite number of white noise series to the signal of interest. These background white noise series provide a time-frequency reference frame for the original signal. The filter bank properties of EMD help the signal components to be projected on the proper scales of this reference frame. Since the white noise series are different in each trial, the noise cancels out for a sufficiently large number of ensembles, leaving only the persistent part of the signals. As a result, the components of similar scales are expected to reside in the same IMFs which reduce the mode mixing problem.10
Vibrocardiographic (VCG) signals are the cardiac vibration measured at the chest surface.13 These signals can contain useful information for diagnosing and monitoring of cardiac conditions.14 However, VCG vibrations have relatively low amplitudes that can be easily contaminated by environmental vibration, patient movements and respiration noise, which can lead to a misinterpretation of the VCG signal features. VCG as well as other biomedical signals such as heart sounds have nonlinear and non-stationary characteristics.15-24 Hence linear methods may not be effective in analyzing these signals. EMD and EEMD were successfully used for noise cancellation and analysis of some biomedical signals.25-30 For example, Velasco MB et al.31 utilized EMD to filter the high-frequency noise and baseline wander of ECG. Nimunkar AJ et al.32 suggested an algorithm to remove power-line noise on ECG by adding a pseudo-high-frequency noise to IMFs. Krupa BN et al.33 proposed an algorithm for denoising the cardiotocography signals using partial sum of IMFs. Lemay M et al.34 compared the performance of an EMD-based algorithm with an IIR band pass filter to improve the quality of atrial signals after QRST cancellation. Chang K et al.35 investigated the effectiveness of EMD-based, EEMD-based and FIR Wiener filters for removing the Gaussian noise from ECG and concluded that EEMD outperformed the other two methods. The current study investigates the utility of different filters for VCG noise cancellation. The performance of EEMD and Wiener filters was compared at different signal to noise ratios for a synthetic VCG signal. In order to assess the performance of different filtering methods, the root-mean-squared misadjustment between the clean and filter VCG amplitudes was calculated. The EEMD-based filter had a lower misadjustment than the Wiener filter. Therefore, this study suggests that the proposed EEMD-based filter may be more effective than Wiener filter in removing white Gaussian noise from actual VCG signals. The organization of this paper is prepared as follows. The Materials and Methods section provides the theoretical background behind EMD and EEMD as well as a brief description of EEMD-based filter and performance evaluation methods. Results are then presented and discussed in the Results and Discussion sections. Finally, a Conclusion section is presented.
Materials and methods
VCG Signal and Synthetic Noise Set
A simulated VCG consisting of a pure tone at 40 Hz and a varying frequency component ranging from 7 to 20 Hz has been used in the present study. To evaluate the capability of EEMD-based filter in noise cancellation, the synthetic VCG signal was polluted by white Gaussian noise sets, nwgn, with the signal-to-noise ratio (SNR) ranging from 1 to 20 dB.
Ensemble Empirical Mode Decomposition
The Hilbert Huang transform is developed for analysis of nonlinear and non-stationary signals. This technique consists of two core steps; empirical mode decomposition and Hilbert transform. The EMD decomposes the signal into IMFs with varying amplitude and frequency. These IMFs are assumed to be correlated to physical or physiological aspects of the signals under analysis.26,36 More specifically, the EMD algorithm consists of the following steps:1
- Identify all the local extrema of the signal, x(t).
- Determine the upper and lower envelopes of the signal with cubic spline using the local maxima and minima, respectively.
- Calculate the local mean of the two envelopes, m(t).
- Calculate the difference between the signal and the local mean, d(t) = x(t)-m(t).
- Replace x(t) with d(t)
- Repeat steps 1 through 5 until d(t) becomes a zero-mean function. Then, d(t) is called the first IMF, c1(t).
- Subtract the IMF from the signal r1(t) = x(t)-c1(t)
- Repeat steps 1 through 7 to obtain the nth IMF after n iterations, cn(t).
- The process stops when rn(t) becomes a monotonic function from which no more IMF can be extracted.
The EEMD that is proposed to solve the mode-mixing issue of the EMD uses the following algorithm:10
- Add a white noise series, ni(t), to the original signal, x(t), to obtain xi(t) = x(t) + ni(t).
- Decompose xi(t) using EMD algorithm
- Repeat steps 1 and 2 with NE (number of ensembles) different sets of white noise series to obtain NE sets of IMFs
- Calculate the mean of the ensemble of IMFs to obtain the final signal intrinsic mode functions.
- At the end of the process, the original signal can be reconstructed as:
(1)
Where ci(t) and r(t) are the ith IMF and residue, respectively. The low and high scale IMFs contain the high-frequency and low-frequency components of the signal, respectively. Thus, EEMD-based low-pass and high-pass filters can be designed using the partial reconstruction of IMFs of interest. Since the white noise series usually has higher frequencies than VCG signals, they are expected to reside in the low scale IMFs. In the current study an EEMD-based low-pass filter was used to remove the undesired noise sets as follows:
(2)
Where
Misadjustment Analysis
The normalized root-mean-square error (NRMSE) between the filter and clean VCGs’ amplitude was calculated as:
(3)
(4)
where
and
are the clean and filtered VCG signal amplitude at time i, respectively.
and L are the maximum amplitude of the clean VCG and the VCG signal length. The performance of the EEMD-based filter was also compared with a Wiener filter37 with a priori SNR estimation using Decision-Directed method.38
Results
The first step of EEMD algorithm consists of adding a finite number of white Gaussian noise series to the signal of interest. The number of added noise (number of ensembles) plays an important role in the EEMD performance. Figure 1 shows the NRMSE of the signal under analysis polluted with different levels of noise versus number of ensembles. The NRMSE decreased dramatically as number of ensembles increased from 1 to 100. For larger number of ensembles, the NRMSE decreased with a slower rate and finally reached a plateau. Large number of ensembles resulted in lower NRMSE, but also required more computational time. Therefore, a compromise between the NRMSE and computational efficiency is needed. In the current study, number of ensembles of 150 was sufficient for the simulated VCG to achieve an acceptable NRMSE value.
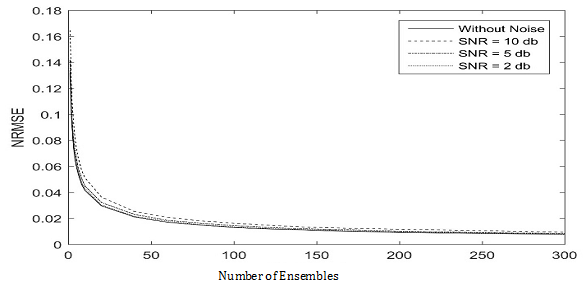
Figure 1 The effect of trial number (number of white noise series) on EEMD performance for reconstructed simulated VCG without added noise and with 10, 5 and 2 dB added noise.
The EEMD-derived IMFs of the simulated VCG with Gaussian noise and their power spectrum are shown in Figure 2. As expected, the EEMD behaved as a filter bank and decomposed the signal into IMF components each of which resided in a specific frequency range. Thus, the noise may be filtered by ignoring the lower IMF scales. Figure 2 shows that the signal is decomposed into 11 oscillatory components and a residue. The lower frequency component of the VCG events (i.e. the varying frequency component ranging from 20 to 7 Hz) was distributed in IMF #2 through #5, while the higher frequency component (i.e. the 40 Hz component) mainly allocated in IMF #2. The high frequency Gaussian noise was concentrated in the first IMF. Therefore, the signal contaminations can be reduced with partial reconstruction of IMF components by ignoring the low scale IMFs. This concept will be investigated further in the following section using the NRMSE parameter.
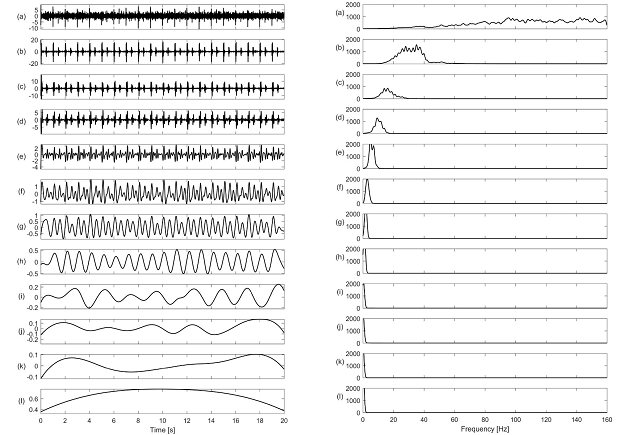
Figure 2 Simulated VCG contaminated by Gaussian noise with SNR=10dB EEMD-derived IMF components (left). The signal was decomposed into 11 IMFs (sub Figure a through k) and a residue (sub Figure l). The power spectral density of the IMFs and residue (right).Most of the high-frequency Gaussian noise is concentrated and localized in the first IMF. However, some low amplitude noise can be seen above 45 Hz in the second IMF. Also, some parts of the VCG events (especially VCG2) are seen in the first IMF between 20-40 Hz which is not desirable.
Discussion
EEMD is a signal-dependent technique that is convenient for nonlinear and non-stationary signals. In this section, the performance and efficiency of the EEMD-based noise filtration method was investigated and compared with traditional filters.
Filtering Performance of EEMD
Figure 3 shows the filtered VCG signals using partial summation of IMF components. The NRMSE between the filtered and clean VCG amplitude are shown in Figure 4. Both EEMD-based filter and the Wiener filter had improved noise cancellation performance as SNR increased. The Wiener filter and EEMDF2 had the minimum NRMSE at 1≤ SNR≤ 2 dB and 4≤ SNR≤ 16 dB, respectively. The ratio EEMDF2/Wiener fell by 48.85% from 1.095 to 0.560 as SNR increased from 1 to 20 dB, which indicates that EEMD-based filter was able to reduce the white Gaussian noise more efficiently than Wiener filter at higher signal-to-noise ratios. Overall, for the signal considered, the EEMD filter outperformed the Wiener filter for SNR values >4 dB and had similar performance for 1< SNR< 4 (Table 1).
NRMSE for Simulated VCG with white noise (%) |
Signal-to-Noise Ratio [dB] |
EEMDF1 |
EEMDF2 |
EEMDF3 |
EEMDF4 |
Wiener |
1 |
22.95 |
13.57 |
16.25 |
21.07 |
12.39 |
2 |
20.5 |
12.46 |
16.01 |
21.15 |
11.06 |
4 |
16.3 |
10.13 |
15.6 |
20.99 |
10.23 |
6 |
12.99 |
8.23 |
15.11 |
20.87 |
9.02 |
8 |
10.39 |
6.82 |
15.04 |
20.83 |
8.56 |
10 |
8.39 |
5.98 |
15.02 |
20.85 |
8.18 |
12 |
6.75 |
5.26 |
14.82 |
20.8 |
7.84 |
14 |
5.55 |
4.85 |
14.93 |
20.79 |
7.52 |
16 |
4.56 |
4.46 |
14.79 |
20.8 |
7.33 |
18 |
3.86 |
4.2 |
14.76 |
20.78 |
7.36 |
20 |
3.32 |
4.07 |
14.8 |
20.87 |
7.26 |
Table 1 NRMSE analysis for simulated VCG contaminated with white noise with SNR values ranging from 1 to 20 dB.
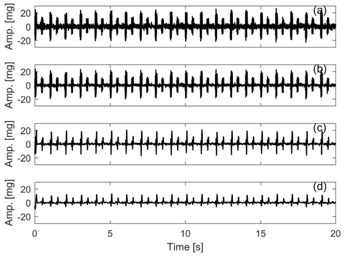
Figure 3 Noise reduction from the simulated VCG contaminated with white Gaussian noise using EEMD-based partial reconstruction.
(A) EEMDF1
(B) EEMDF2
(C) EEMDF3
(D) EEMDF4
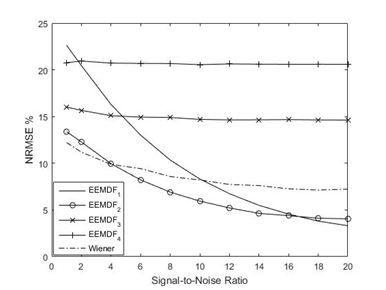
Figure 4 NRMSE analysis for simulated VCG contaminated with white noise with SNR values ranging from 1 to 20 dB.
EMD and EEMD were designed to analyze nonlinear and non-stationary signals. The main advantage of EMD is that it is an adaptive method that depends only on the signal under analysis and does not require any a priori defined basis system. Instead, it decomposes the signal into IMFs that depend on the original signal alone. On the other hand, determining the physical phenomena associated with IMFs is not always possible and needs comprehensive understanding of the signal.39 A main drawback of EMD is the “mode mixing”, which is either a similar scale residing in more than one IMF or an IMF consisting of signals of broadly different scales.10 This issue may cause some IMFs to become physically meaningless. EEMD was developed to overcome the EMD mode mixing issue. However, EEMD has relatively higher computational cost than both EMD and traditional band-pass filters. In the current study, EEMD was more effective than Wiener filter in white noise removal from VCG. The filter performance certainly depended on the number of IMFs left out. Performance was best in the current application when only the lowest IMF with the lowest scale is ignored.
Conclusion
Noise removal from biological signals like VCG can help provide higher quality information that would facilitate signal interpretation, which may help provide more accurate medical diagnosis. In the current study, the performance of EEMD-based filter for white noise removal from VCG signal was evaluated. To test the filter, a synthetic VCG signal was created and corrupted by white noise. The filter was then used to recover the original VCG signal. This was followed by calculating the normalized root-mean-squared misadjustment between the original and filtered signals. The performance of the EEMD and a Wiener filter was evaluated by comparing the associated misadjustments. Results of this analysis demonstrated that the EEMD filter had a lower normalized root-mean-squared misadjustment than the Wiener filter. The lower performance of the Wiener filter may be attributed to a relatively high non-linearity of the VCG signal under consideration. More studies may be warranted to document the effectiveness of EEMD filters for noise cancellation from actual VCG signals in health and disease. Future studies may also investigate the connection between the IMF and cardiac events, which in turn, may enhance our understanding of VCG signals and their relation to cardiac events.
Acknowledgements
This work was partially supported by NIH R01 EB012142, R43 HL099053.
Conflict of interest
The author declares no conflict of interest.
References
- Huang NE, Shen Z, Long SR, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc A Math Phys Eng Sci. 1998;454(1971):903–995.
- Rehman N, Mandic DP. Empirical mode decomposition for trivariate signals. IEEE Transactions on Signal Processing. 2010;58(3):1059–1068.
- Lee PL, Shang LZ, Wu YT, et al. Single-trial analysis of cortical oscillatory activities during voluntary movements using empirical mode decomposition (emd)-based spatiotemporal approach. Ann Biomed Eng. 2009;37(8):1683–1700.
- Mijović B, De Vos M, Gligorijević I, et al. Source separation from single-channel recordings by combining empirical-mode decomposition and independent component analysis. IEEE Trans Biomed Eng. 2010;57(9):2188–2196.
- Zhang Y, Gao Y, Wang L, et al. The removal of wall components in doppler ultrasound signals by using the empirical mode decomposition algorithm. IEEE Trans Biomed Eng. 2007;54(9):1631–1642.
- Salisbury JI, Sun Y. Assessment of chaotic parameters in nonstationary electrocardiograms by use of empirical mode decomposition. Ann Biomed Eng. 2004;32(10):1348–1354.
- Wang Z, Maier A, Logothetis NK, et al. Single-Trial classification of bistable perception by integrating empirical mode decomposition, clustering, and support vector machine. Eurasip J Adv Signal Process. 2008;2008:592742.
- Coughlin KT, Tung KK. 11-Year solar cycle in the stratosphere extracted by the empirical mode decomposition method. Advances in Space Research. 2004;34(2):323–329.
- Cong F, Sipola T, Scott TH, et al. Hilbert-Huang versus Morlet wavelet transformation on mismatch negativity of children in uninterrupted sound paradigm. Nonlinear Biomed Phys. 2009;3(1):1.
- Zhaohua Wu, Huang NE. Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adapt Data Anal. 2009;1(1):1–41.
- Zhaohua Wu, Huang NE. A study of the characteristics of white noise using the empirical mode decomposition method. Proc R Soc Lond A. 2004;460:1597–1611.
- Flandrin P, Rilling G, Gonçalvés P. Empirical mode decomposition as a filter bank. IEEE Signal Processing Letters. 2004;11(2):112–114.
- Taebi A, Mansy HA. Time-frequency Analysis of Vibrocardiographic Signals. BMES annual meeting, USA: University of Central Florida; 2015.
- Inan OT, Migeotte PF, Park KS, et al. Ballistocardiography and seismocardiography: a review of recent advances. IEEE J Biomed Health Inform. 2015;19(4):1414–1427.
- Visagie C. Screening for abnormal heart sounds and murmurs by implementing neural networks. Stellenbosch. South Africa: University of Stellenbosch; 2007.
- Taebi A. Mechanical energy exchange during plane walking and stepping over obstacle in subjects with Down syndrome. Italy: Politecnico di Milano-Biblioteca Centrale di Architettura; 2013.
- Salami F, Vimercati SL, Rigoldi C, et al. Mechanical energy assessment of adult with Down syndrome during walking with obstacle avoidance. Res Dev Disabil. 2014;35(8):1856–1862.
- Taebi A, Mansy HA. Time-frequency Description of Vibrocardiographic Signals. 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, USA: IEEE; 2016.
- Taebi A, Mansy HA. Effect of noise on time-frequency analysis of vibrocardiographic signals. J J Bioengineer & Biomedical Sci. 2016;6:202.
- Mansy HA, Royston TJ, Balk RA, et al. Pneumothorax detection using computerised analysis of breath sounds. Med Biol Eng Comput. 2002;40(5):526–532.
- Mansy HA, Royston TJ, Balk RA, et al. Pneumothorax detection using pulmonary acoustic transmission measurements. Med Biol Eng Comput. 2002;40(5):520–525.
- Mansy HA, Royston TJ, Sandler RH. Use of abdominal percussion for pneumoperitoneum detection. Med Biol Eng Comput. 2002;40(4):439–446.
- Mansy HA, Sandler RH. Detection and analysis of gastrointestinal sounds in normal and small bowel obstructed rats. Med Biol Eng Comput. 2000;38(1):42–48.
- Khalili F, Mansy HA. Blood flow through a dysfunctional mechanical heart valve. 38th Annual international conference of the IEEE engineering in medicine and biology society, Orlando, USA: IEEE; 2016.
- Wu MC, Hu CK. Empirical mode decomposition and synchrogram approach to cardiorespiratory synchronization. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;73(5 Pt 1):051917.
- Samit Ari, Goutam Saha. Classification of heart sounds using empirical mode decomposition based features. Int J of Medical Engineering and Informatics. 2008;1(1):91–108.
- Chappell MA, Payne SJ. A method for the automated detection of venous gas bubbles in humans using empirical mode decomposition. Ann Biomed Eng. 2005;33(10):1411–1421.
- Lee J, McManus DD, Merchant S, et al. Automatic motion and noise artifact detection in holter ECG data using empirical mode decomposition and statistical approaches. IEEE Trans Biomed Eng. 2012;59(6):1499–1506.
- Huang W, Shen Z, Huang NE, et al. Engineering analysis of biological variables: an example of blood pressure over 1 day. Proc Natl Acad Sci U S A. 1998;95:4816–4821.
- Huang W, Shen Z, Huang NE, et al. Use of intrinsic modes in biology: examples of indicial response of pulmonary blood pressure to +/- step hypoxia. Proc Natl Acad Sci U S A. 1998;95(22):12766–12771.
- Velasco MB, Weng B, Barner KE. ECG signal denoising and baseline wander correction based on the empirical mode decomposition. Comput Biol Med. 2008;38(1):1–13.
- Nimunkar AJ, Tompkins WJ. EMD-based 60-Hz noise filtering of the ECG. 29th annual international conference of the IEEE engineering in medicine and biology society, USA: IEEE; 2007. p. 1904–1907.
- Krupa BN, Ali MAM, Zahedi E. The application of empirical mode decomposition for the enhancement of cardiotocograph signals. Physiol Meas. 2009;30(8):729.
- Lemay M, Vesin JM. QRST cancellation based on the empirical mode decomposition. Computers in Cardiology. 2006;33:561–564.
- Chang KM, Liu SH. Gaussian noise filtering from ECG by Wiener filter and ensemble empirical mode decomposition. J Signal Process Syst. 2011;64(2):249–264.
- Balocchi R, Menicucci D, Santarcangelo E, et al. Deriving the respiratory sinus arrhythmia from the heartbeat time series using empirical mode decomposition. Chaos, Solitons & Fractals. 2004;20(1):171–177.
- Wiener N. Extrapolation, interpolation and smoothing of stationary time series. USA: The MIT Press; 1964.
- Scalart P, Filho JV. Speech enhancement based on a priori signal to noise estimation. IEEE Int Conf Acoust Speech Signal Process Conf Proc. 1996;2:629–632.

©2017 Taebi, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.






