Journal of
eISSN: 2572-8466


Review Article Volume 2 Issue 4
Petroleum Engineering Department, Universiti Technologi Petronas, Malaysia
Correspondence: GM Hamada, Petroleum Engineering Department, Faculty of Geosciences and Petroleum Engineering, Universiti Technologi Petronas, Malaysia
Received: October 24, 2016 | Published: March 6, 2017
Citation: Hamada GM. Effect of non-hydrocarbon components on gas compressibility factor values and correlations. J Appl Biotechnol Bioeng. 2017;2(4):124-134. DOI: 10.15406/jabb.2017.02.00036
Gas compressibility factor is necessary in most natural gas engineering calculations. The most common sources of z-factor values are experimental measurements, equation of state and empirical correlations. There are more than twenty correlations available with two variables for calculating the z-factor from fitting Standing-Katz chart values in EOS or through fitting technique. The theory of corresponding states dictates that the Z-factor can be uniquely defined as function of reduced pressure and temperature. Natural gases frequently contain material other than hydrocarbon components, such as nitrogen, carbon dioxide and hydrogen sulfide. Hydrocarbon gases are classified as sweet or sour depending on the hydrogen sulfide content. Both sweet and sour gases may contain nitrogen, carbon dioxide or both. The compositions of most natural gases are hydrocarbon of the same family (paraffin hydrocarbons), so the correlation of this type is possible but containing non-hydrocarbon on the gases, make the prediction difficult. This paper focuses on evaluating the correlations which calculate gas compressibility factor for natural gas reservoirs contains non-hydrocarbon components. It is found that gas pseudo-critical temperature decreases with the increase of N2 and H2S. Also, it is observed that in the tested gas reservoirs which contain C7+ by Stewart Mixing Rules and Kay’s there are some deviation on z factor between two methods that became negligible by using the correction method for non-hydrocarbon.
Keywords: mole fraction (H2S+CO2), mole fraction of H2S, temperature, pressure, impurities
Pc, critical pressure; Ppr, pseudo-reduced pressure; Ppc, pseudo critical pressure; P’pc, corrected pseudo critical pressure; Tc, critical temperature; Tpr, pseudo reduced temperature; Tpc, pseudo-critical temperature; T’pc, corrected pseudo critical temperature; Ɛ, pseudo-critical temperature adjustment factor; CO2, carbon dioxide; SK, standing and Katz; DK, dranchuk- abou- kassem; SBV, stewart-burkhardt-voo
Gas compressibility factor is involved in calculating gas properties such as formation volume factor, density, compressibility and viscosity. All these properties are necessary in the oil and gas industry for evaluating newly discovered gas reservoirs, calculating initial gas reserves, predicting future gas production and designing production tubing and pipelines. The accurate measurement of natural gas related fluids is difficult. The compressibility factor is a ubiquitous concept in measurement. It arises in many industry practices and standard. The industry standard is to measure gas properties, pressure-volume-temperature in the laboratory using reservoir samples. The drawback is that these isothermally measured PVT data is applicable at measures pressure and reservoir temperature. Calculation Methods such as correlations and equation of state are used to predict properties at other pressure and temperature. Also, laboratory analyses for PVT behavior are sometimes expensive and time consuming. Correlations, which are used to predict gas compressibility factor, are much easier and faster than equation of state. Natural gases frequently contain material other than hydrocarbon components, such as nitrogen, carbon dioxide and hydrogen sulfide. Hydrocarbon gases are classified as sweet or sour depending on the hydrogen sulfide content. Both sweet and sour gases may contain nitrogen, carbon dioxide or both. Sometimes these correlations have comparable accuracy to equation of state. Predicting compressibility factor for gas containing non-hydrocarbon (impurities) is much difficult than that for sweet gas. The compositions of most natural gases are hydrocarbon of the same family (paraffin hydrocarbons), so the correlation of this type is possible but containing non-hydrocarbon on the gases, make the prediction difficult. Therefore, several attempts have been made to predict compressibility factor for sweet gases, Wichert and Aziz and Carr-Kobayashi-Burrows presented correction for the presences of hydrogen sulfide and carbon dioxide for determining the compressibility factor. The objective of this study is evaluating the pervious correlations which calculate gas compressibility factor for gases contain non-hydrocarbon component and observe the effect of these component on Z factor.1-5,8
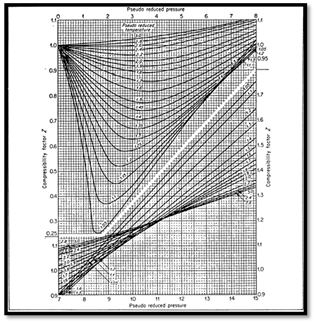
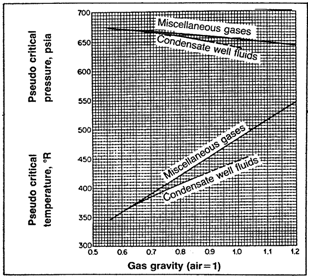
The most common method is to use one of the forms of the principle of corresponding states. In this form, gas compressibility factor is expressed as function of pseudo-reduced pressure and temperature (Ppr, Tpr). Compressibility factors are function of composition as well as temperature and pressure. Standing and Katz (SK) presented a chart for determining gas compressibility factor based on the principle of corresponding states. The SK chart was prepared for binary mixture of low molecular weight sweet gases. Several mathematical expressions fitting the SK chart have been proposed to calculate the gas compressibility factor. Dranchuk- Abou- Kassem (DK) correlation is the most accurate representation of SK chart. When dealing with gas mixture, the gas mixture is critical pressure (Ppc) and temperature (Tpc) are required. Critical properties of natural gas are calculated from either gas composition or gas gravity. Several Mixing rules have been proposed to calculate mixture critical properties of natural gases. Among these methods, Kay’s mixing rule and stewart-Burkhardt-Voo (SBV) are the most widely used. Kay’s mixing rule is simple and provides an accurate determination of gas compressibility factor for sweet gases of low molecular weight. Satter and Campbell evaluated several mixing rules for calculating properties of natural gases.6-8 They concluded that Stewart-Burkhardt-Voo rule known as SBV provided the most satisfactory results especially for gases of high molecular weight. Sutton studied the performance of several mixing rule for calculating compressibility factor for gas condensates that contain a large amount of heptanes plus fraction. Sutton modified SBV mixing rule to account for the presence of heptanes plus in the natural gases. Standard laboratory analysis gives composition of natural gases through hexane and lump components heavier than hexane in heptane plus fraction known as C7+ critical properties of pure components are well documents as shown Table 1. The critical properties of the C7+, fraction are calculated from correlations using molecular weight and specific gravity of the heptanes plus. Standing presented correlation of pseudo critical properties to gas gravity based on low molecular weight which are:
(1)
(2)
Component |
Molecular weight |
Critical pressure (Psia) |
Critical Temperature(Ro) |
H2S |
34.08 |
1300 |
672.45 |
CO2 |
44.01 |
1071 |
547.45 |
N2 |
28.01 |
493 |
227.27 |
C1 |
16.04 |
667.8 |
343.04 |
C2 |
30.07 |
707.8 |
549.76 |
C3 |
44.01 |
616.3 |
665.68 |
i-C4 |
58.12 |
529.1 |
734.65 |
n-C4 |
58.12 |
550.7 |
765.32 |
i-C5 |
72.15 |
490.4 |
828.77 |
n-C5 |
72.15 |
488.6 |
845.37 |
C6 |
86.18 |
436.9 |
913.37 |
Table 1 Physical Properties of defined component.
The previous correlation work only when there no non-hydrocarbon gases present on the gases. Sutton developed the following correlation work with high molecular weight of gases.
(3)
(4)
The gases which Suttton used to develop previous correlation were sweet gases with minor amount of carbon dioxide and nitrogen and no hydrogen sulfide. Then, Elsharkawy AM et al. 1 developed Sutton correlation but will cover heavier hydrocarbons and minor of hydrogen sulfide.
(6)
(7)
Methods of Calculating the Pseudo-critical Gas Properties
The pseudo-critical properties provide a mean to correlate the physical properties of mixtures with principle of the corresponding states. The principle of corresponding states suggests that pure but similar gases have the same gas deviation or Z factor at the same values of reduced pressure and temperature. The mixture of chemically similar gases can be correlated with reduced temperature and reduced pressure.9,10 There are several methods which are:
The theory corresponding states dictates that the Z-factor can be uniquely defined as function of reduced pressure and temperature. The reduce pressure and temperatures are:
(7)
The values of pseudo-critical pressure and temperature can be estimated from the following equations if the composition of the gas and the critical properties of the individual component are known (kay):
(8)
Procedures for Stewart Mixing Rules
(9)
(10)
(11)
(12)
(13)
(12)
and (13)
(14)
(15)
Procedures for Sutton’s correlations of sweet gas
(16)
(17)
Procedures for Sutton’s correlations of Sour gas
(18)
(19)
(20)
Methods of Correction the Pseudo-critical Gas Properties for H2S and CO2 contamination.
Natural gases, which contain H2S and CO2 frequently, exhibit different compressibility factor behavior than do sweet gases. Wichert and Aziz developed a simple, easy to use calculation procedure to account for these differences.
Wichert-Aziz Correction Method
This method permits the use of the standing-Katz chart, by using a pseudo-critical temperature adjustment factor, which is function of the concentration of CO2 and H2S in the sour gas. The following Wichert and Aziz correlation is also can obtain from Figure 2:
(20)
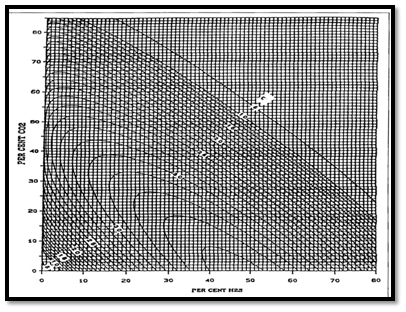
Where the pseudo-critical temperature, T’pc and pressure P’pc , adjusted for CO2 and H2S contamination are :
(21)
Where,
A: Sum of the mole fractions of H2S and CO2 in the gas mixture
B: Mole fraction of H2S in the gas mixture.
Methods of Correction the Pseudo-critical Gas Properties for N2 and H2O vapor contamination
Carr-Kobayashi and Burrows developed a simple procedure to adjust the pseudo-critical properties of natural gases when non-hydrocarbon components are present.
Carr-Kobayashi and Burrows Correction Method
The procedures to obtain the correction are following:
(22)
(23)
(24)
Where, T’Pc and P’pc are the pseudo-critical temperature and pressure corrected for H2S and CO2 with wichert and Aziz correlation.
The data are analyzed and Stewart method and Kay’s mixing rules for predicting pseudo-reduce pressure and temperatures are used for these data with knowing composition. Moreover, according to present of non-hydrocarbon on the data I used the correction methods which are Wichert- Aziz and Carr-Kobayashi and Burrows. The data of three reservoirs (A,B,C) with water vapor, carbon dioxide and hydrogen sulfide but with light molecular weight while ,the others (D,E,F) have C7+ and without water vapor are shown in Table 2, so I used Stewart Mixing Rules and Kays, The calculation and result for six reservoir are appear in Tables 3-14. From calculation, it is found that gas pseudo-critical temperature decrease with increase of N2 as shown in Figure 4. Moreover, pseudo-critical temperature with increasing H2S is decreases with limitation as shown in Figure 5 then slightly increase with increase temperature maybe it related to the behavior of H2S in reservoir. In addition, gas pseudo-critical pressure increase with increase N2 and H2S as shown in Figure 5 & 8. Also, it is observed that in the tested gas reservoirs which contain C7+ by Stewart Mixing Rules and Kay’s there are some deviation on z factor between two methods that became negligible by using the correction method for non-hydrocarbon as shown in Figure 8 and Table 10 &14. It is obvious from the error of Z factor calculated by Stewart for reservoirs D, E and F (Table 10) is lower than Z error for reservoirs A, B and C (Table 6) with Kay’s technique, therefore it is recommended to adopt Stewart Mixing Rules to solve the problem on non-hydrocarbon impurities in natural gas behavior and more specifically Z factor
A |
B |
C |
D |
E |
F |
|
Pressure(psia) |
6000 |
5200 |
5000 |
4010 |
2640 |
2748 |
Temperature (Ro) |
673.8 |
657.6 |
657.6 |
711.6 |
672 |
690 |
C1 |
59.59 |
69.14 |
71.32 |
57.95 |
61.83 |
40 |
C2 |
0.02 |
2.27 |
0.1 |
12.59 |
7.7 |
11.93 |
C3 |
0.01 |
1.96 |
0 |
7.94 |
7.63 |
14 |
i-C4 |
0 |
0.46 |
0 |
1.13 |
1.73 |
4.7 |
n-C4 |
0 |
1.46 |
0 |
3.16 |
4.38 |
7.37 |
i-C5 |
0 |
0 |
0 |
1.42 |
2.38 |
2.38 |
n-C5 |
0 |
0 |
0 |
2.01 |
2.6 |
5.6 |
C6 |
0 |
0 |
0 |
2.18 |
4.34 |
7.54 |
C7+ |
0 |
0 |
0 |
4.54 |
6.87 |
5.93 |
CO2 |
12.59 |
7.9 |
9.05 |
3.9 |
0.3 |
0.34 |
N2 |
11.95 |
0.1 |
6.35 |
0.2 |
0.24 |
0.21 |
H2S |
12.09 |
13.03 |
9.44 |
2.98 |
0 |
0 |
H2O |
3.75 |
3.68 |
3.74 |
0 |
0 |
0 |
Table 2 Six different reservoir in Abu-Dhabi.
Component |
Yi |
Mi |
YiMi |
Tci |
YiTci |
Pci |
YiPci |
CO2 |
0.1259 |
44 |
5.5396 |
547.6 |
68.94284 |
1071 |
134.8389 |
N2 |
0.1198 |
28 |
3.3544 |
239.3 |
28.66814 |
507.5 |
60.7985 |
H2S |
0.1209 |
34 |
4.1106 |
672.35 |
81.28712 |
1306 |
157.8954 |
H20 |
0.0375 |
18 |
0.675 |
1164.85 |
43.68188 |
3200.1 |
120.0038 |
C1 |
0.5956 |
16 |
9.5296 |
343 |
204.2908 |
666.4 |
396.9078 |
C2 |
0.0002 |
30 |
0.006 |
549.6 |
0.10992 |
706.5 |
0.1413 |
C3 |
0.0001 |
45 |
0.0045 |
665.7 |
0.06657 |
616 |
0.0616 |
i-C4 |
0 |
58 |
0 |
734.1 |
0 |
527.9 |
0 |
n-C4 |
0 |
58 |
0 |
765.3 |
0 |
550.6 |
0 |
Total |
1 |
23.2197 |
427.0473 |
870.6473 |
Table 3 Reservoir A using Kay’s Rule at P=6000psi and T=673.8Ro.
Component |
Yi |
Mi |
YiMi |
Tci |
YiTci |
Pci |
YiPci |
CO2 |
0.079 |
44 |
3.476 |
547.6 |
43.2604 |
1071 |
84.609 |
N2 |
0.001 |
28 |
0.028 |
239.3 |
0.2393 |
507.5 |
0.5075 |
H2S |
0.1303 |
34 |
4.4302 |
672.35 |
87.60721 |
1306 |
170.1718 |
H20 |
0.0368 |
18 |
0.6624 |
1164.85 |
42.86648 |
3200.1 |
117.7637 |
C1 |
0.6914 |
16 |
11.0624 |
343 |
237.1502 |
666.4 |
460.749 |
C2 |
0.0227 |
30 |
0.681 |
549.6 |
12.47592 |
706.5 |
16.03755 |
C3 |
0.0196 |
45 |
0.882 |
665.7 |
13.04772 |
616 |
12.0736 |
i-C4 |
0.0046 |
58 |
0.2668 |
734.1 |
3.37686 |
527.9 |
2.42834 |
n-C4 |
0.0146 |
58 |
0.8468 |
765.3 |
11.17338 |
550.6 |
8.03876 |
Total |
1 |
22.3356 |
451.1975 |
872.3792 |
Table 4 Reservoir B using Kay’s Rule at P=5200psi and T=657.6Ro.
Component |
Yi |
Mi |
YiMi |
Tci |
YiTci |
Pci |
YiPci |
CO2 |
0.0905 |
44 |
3.982 |
547.6 |
49.5578 |
1071 |
96.9255 |
N2 |
0.0635 |
28 |
1.778 |
239.3 |
15.19555 |
507.5 |
32.22625 |
H2S |
0.0944 |
34 |
3.2096 |
672.35 |
63.46984 |
1306 |
123.2864 |
H20 |
0.0374 |
18 |
0.6732 |
1164.85 |
43.56539 |
3200.1 |
119.6837 |
C1 |
0.7132 |
16 |
11.4112 |
343 |
244.6276 |
666.4 |
475.2765 |
C2 |
0.001 |
30 |
0.03 |
549.6 |
0.5496 |
706.5 |
0.7065 |
C3 |
0 |
45 |
0 |
665.7 |
0 |
616 |
0 |
i-C4 |
0 |
58 |
0 |
734.1 |
0 |
527.9 |
0 |
C5 |
0 |
72 |
0 |
828.77 |
0 |
490.4 |
0 |
Total |
1 |
21.084 |
416.9658 |
848.1049 |
Table 5 Reservoir C using Kay’s Rule at P=5000psi and T=657.6 Ro.
A |
B |
C |
|
PPc |
870.647 |
872.379 |
848.105 |
TPc |
427.047 |
451.197 |
416.966 |
PPr |
6.891 |
5.961 |
5.895 |
TPr |
1.578 |
1.457 |
1.577 |
Z |
0.928 |
0.848 |
0.872 |
Tpc' |
400.563 |
426.246 |
394.149 |
Ppc' |
811.305 |
819.004 |
797.964 |
Tp'' |
376.709 |
412.673 |
373.208 |
PP'' |
778.462 |
774.854 |
756.788 |
Tr |
1.789 |
1.594 |
1.762 |
Pr |
7.708 |
6.711 |
6.607 |
z |
1.004 |
0.92 |
0.946 |
(Z- Error) |
0.0089 |
0.0065 |
0.0178 |
Table 6 Properties and Compressibility factor for the three Reservoirs.
Component |
Yi |
Mi |
yiMi |
Tci (◦R) |
Pci (psia) |
yiTci/Pci |
yi√Tci/Pci |
yiTci/√Pci |
N2 |
0.002 |
28.01 |
0.06 |
227.16 |
493.1 |
0 |
0 |
0.02 |
CH4 |
0.5795 |
16.04 |
9.3 |
343 |
666.4 |
0.3 |
0.42 |
7.7 |
C2H6 |
0.1259 |
30.07 |
3.79 |
549.59 |
706.5 |
0.1 |
0.11 |
2.6 |
C3H8 |
0.0794 |
44.1 |
3.5 |
665.73 |
616 |
0.09 |
0.08 |
2.13 |
i-C4H10 |
0.0113 |
58.12 |
0.66 |
734.13 |
527.9 |
0.02 |
0.01 |
0.36 |
n-C4H10 |
0.0316 |
58.12 |
1.84 |
765.29 |
550.6 |
0.04 |
0.04 |
1.03 |
i-C5H12 |
0.0142 |
72.15 |
1.02 |
828.77 |
490.4 |
0.02 |
0.02 |
0.53 |
n-C5H12 |
0.0201 |
72.15 |
1.45 |
845.47 |
488.6 |
0.03 |
0.03 |
0.77 |
C6H14 |
0.0218 |
86.18 |
1.88 |
913.27 |
436.9 |
0.05 |
0.03 |
0.95 |
C7+ |
0.0454 |
114.23 |
5.19 |
1005.3 |
375.5 |
0.12 |
0.07 |
2.36 |
CO2 |
0.039 |
44.01 |
1.72 |
547.45 |
1071 |
0.02 |
0.03 |
0.65 |
H2S |
0.0298 |
34 |
1.01 |
672.35 |
1306 |
0.02 |
0.02 |
0.55 |
∑ |
1 |
30.39 |
0.8 |
0.86 |
19.66 |
Table 7 Reservoir D using Stewart Mixing Rules.
Component |
Yi |
Mi |
yiMi |
Tci (◦R) |
Pci (psia) |
yiTci/Pci |
yi√Tci/Pci |
yiTci/√Pci |
N2 |
0.0024 |
28.01 |
0.07 |
227.16 |
493.1 |
0 |
0 |
0.02 |
CH4 |
0.6183 |
16.04 |
9.92 |
343 |
666.4 |
0.32 |
0.44 |
8.22 |
C2H6 |
0.077 |
30.07 |
2.32 |
549.59 |
706.5 |
0.06 |
0.07 |
1.59 |
C3H8 |
0.0763 |
44.1 |
3.36 |
665.73 |
616 |
0.08 |
0.08 |
2.05 |
i-C4H10 |
0.0173 |
58.12 |
1.01 |
734.13 |
527.9 |
0.02 |
0.02 |
0.55 |
n-C4H10 |
0.0438 |
58.12 |
2.55 |
765.29 |
550.6 |
0.06 |
0.05 |
1.43 |
i-C5H12 |
0.0238 |
72.15 |
1.72 |
828.77 |
490.4 |
0.04 |
0.03 |
0.89 |
n-C5H12 |
0.026 |
72.15 |
1.88 |
845.47 |
488.6 |
0.04 |
0.03 |
0.99 |
C6H14 |
0.0434 |
86.18 |
3.74 |
913.27 |
436.9 |
0.09 |
0.06 |
1.9 |
C7+ |
0.0687 |
114.23 |
7.85 |
1005.3 |
375.5 |
0.18 |
0.11 |
3.56 |
CO2 |
0.003 |
44.01 |
0.13 |
547.45 |
1071 |
0 |
0 |
0.05 |
∑ |
1 |
34.4 |
0.91 |
0.91 |
21.26 |
Table 8 Reservoir E using Stewart Mixing Rules.
Component |
Yi |
Mi |
yiMi |
Tci (◦R) |
Pci (psia) |
yiTci/Pci |
yi√Tci/Pci |
yiTci/√Pci |
N2 |
0 |
28.01 |
0.06 |
227.16 |
493.1 |
0 |
0 |
0.02 |
CH4 |
0.4 |
16.04 |
6.42 |
343 |
666.4 |
0.21 |
0.29 |
5.31 |
C2H6 |
0.12 |
30.07 |
3.59 |
549.59 |
706.5 |
0.09 |
0.11 |
2.47 |
C3H8 |
0.14 |
44.1 |
6.17 |
665.73 |
616 |
0.15 |
0.15 |
3.76 |
i-C4H10 |
0.05 |
58.12 |
2.73 |
734.13 |
527.9 |
0.07 |
0.06 |
1.5 |
n-C4H10 |
0.07 |
58.12 |
4.28 |
765.29 |
550.6 |
0.1 |
0.09 |
2.4 |
i-C5H12 |
0.02 |
72.15 |
1.72 |
828.77 |
490.4 |
0.04 |
0.03 |
0.89 |
n-C5H12 |
0.06 |
72.15 |
4.04 |
845.47 |
488.6 |
0.1 |
0.07 |
2.14 |
C6H14 |
0.08 |
86.18 |
6.5 |
913.27 |
436.9 |
0.16 |
0.11 |
3.29 |
C7+ |
0.06 |
114.23 |
6.77 |
1005.3 |
375.5 |
0.16 |
0.1 |
3.08 |
CO2 |
0 |
44.01 |
0.15 |
547.45 |
1071 |
0 |
0 |
0.06 |
∑ |
1 |
42.43 |
1.07 |
0.99 |
24.92 |
|||
Table 9 Reservoir F using Stewart Mixing Rule.
D |
E |
F |
|
Fj |
0.044 |
0.07 |
0.059 |
Ej |
0.007 |
0.002 |
0.004 |
Ek |
0.355 |
0.397 |
0.38 |
J |
0.762 |
0.851 |
1.017 |
K |
19.66 |
21.256 |
24.924 |
J' |
0.756 |
0.849 |
1.013 |
K' |
19.305 |
20.859 |
24.544 |
Tpc |
493.256 |
512.496 |
594.9 |
Ppc |
652.851 |
603.662 |
587.495 |
Tpc' |
481.534 |
511.864 |
594.193 |
Ppc' |
636.898 |
602.917 |
586.797 |
Tp'' |
493.263 |
511.958 |
594.448 |
PP'' |
653.206 |
602.792 |
586.654 |
Tr |
1.478 |
1.313 |
1.161 |
Pr |
6.296 |
4.379 |
4.684 |
Z |
0.874 |
0.69 |
0.666 |
Z-Error % |
0.0023 |
0.0056 |
0.0102 |
Table 10 Properties and Compressibility factor for the three Reservoirs.
Component |
yi |
Mi |
Tci (◦R) |
Pci (psia) |
yiTci |
yiPci |
N2 |
0.002 |
28 |
227.2 |
493.1 |
0.5 |
1 |
CH4 |
0.58 |
16 |
343 |
666.4 |
198.8 |
386.2 |
C2H6 |
0.126 |
30.1 |
549.6 |
706.5 |
69.2 |
88.9 |
C3H8 |
0.079 |
44.1 |
665.7 |
616 |
52.9 |
48.9 |
i-C4H10 |
0.011 |
58.1 |
734.1 |
527.9 |
8.3 |
6 |
n-C4H10 |
0.032 |
58.1 |
765.3 |
550.6 |
24.2 |
17.4 |
i-C5H12 |
0.014 |
72.2 |
828.8 |
490.4 |
11.8 |
7 |
n-C5H12 |
0.02 |
72.2 |
845.5 |
488.6 |
17 |
9.8 |
C6H14 |
0.022 |
86.2 |
913.3 |
436.9 |
19.9 |
9.5 |
C7+ |
0.045 |
114.2 |
1005.3 |
375.5 |
45.6 |
17 |
CO2 |
0.039 |
44 |
547.5 |
1071 |
21.4 |
41.8 |
H2S |
0.03 |
34 |
672.4 |
1306 |
20 |
38.9 |
∑ |
1 |
8097.5 |
7728.9 |
489.5 |
672.4 |
Table 11 Reservoir D using Kay’s Mixing Rules.
Component |
yi |
Mi |
Tci (◦R) |
Pci (psia) |
yiTci |
yiPci |
N2 |
0.0024 |
28 |
227.2 |
493.1 |
0.5 |
1.2 |
CH4 |
0.6183 |
16 |
343 |
666.4 |
212.1 |
412 |
C2H6 |
0.077 |
30.1 |
549.6 |
706.5 |
42.3 |
54.4 |
C3H8 |
0.0763 |
44.1 |
665.7 |
616 |
50.8 |
47 |
i-C4H10 |
0.0173 |
58.1 |
734.1 |
527.9 |
12.7 |
9.1 |
n-C4H10 |
0.0438 |
58.1 |
765.3 |
550.6 |
33.5 |
24.1 |
i-C5H12 |
0.0238 |
72.2 |
828.8 |
490.4 |
19.7 |
11.7 |
n-C5H12 |
0.026 |
72.2 |
845.5 |
488.6 |
22 |
12.7 |
C6H14 |
0.0434 |
86.2 |
913.3 |
436.9 |
39.6 |
19 |
C7+ |
0.0687 |
114.2 |
1005.3 |
375.5 |
69.1 |
25.8 |
CO2 |
0.003 |
44 |
547.5 |
1071 |
1.6 |
3.2 |
∑ |
1 |
7425.2 |
6422.9 |
504 |
620.2 |
Table 12 Reservoir E using Kay’s Mixing Rules.
Component |
yi |
Mi |
Tci (◦R) |
Pci (psia) |
yiTci |
yiPci |
N2 |
0.0021 |
28 |
227.2 |
493.1 |
0.5 |
1 |
CH4 |
0.4 |
16 |
343 |
666.4 |
137.2 |
266.6 |
C2H6 |
0.1193 |
30.1 |
549.6 |
706.5 |
65.6 |
84.3 |
C3H8 |
0.14 |
44.1 |
665.7 |
616 |
93.2 |
86.2 |
i-C4H10 |
0.047 |
58.1 |
734.1 |
527.9 |
34.5 |
24.8 |
n-C4H10 |
0.0737 |
58.1 |
765.3 |
550.6 |
56.4 |
40.6 |
i-C5H12 |
0.0238 |
72.2 |
828.8 |
490.4 |
19.7 |
11.7 |
n-C5H12 |
0.056 |
72.2 |
845.5 |
488.6 |
47.3 |
27.4 |
C6H14 |
0.0754 |
86.2 |
913.3 |
436.9 |
68.9 |
32.9 |
C7+ |
0.0593 |
114.2 |
1005.3 |
375.5 |
59.6 |
22.3 |
CO2 |
0.0034 |
44 |
547.5 |
1071 |
1.9 |
3.6 |
∑ |
1 |
6877.7 |
5351.9 |
584.8 |
601.4 |
Table 13 Reservoir F using Kay’s Mixing Rules.
D |
E |
F |
|
Tpc |
489.453 |
504.005 |
584.759 |
Ppc |
672.432 |
620.215 |
601.395 |
Tpc' |
477.731 |
503.373 |
584.052 |
Ppc' |
655.874 |
619.437 |
600.668 |
Tp'' |
477.741 |
503.446 |
584.759 |
PP'' |
655.876 |
619.352 |
601.395 |
Tr |
1.49 |
1.335 |
1.181 |
Pr |
6.114 |
4.263 |
4.576 |
Z |
0.865 |
0.691 |
0.663 |
Table 14 Properties and Compressibility factor for the three Reservoirs.
Natural gases, which contain H2S and CO2 frequently, exhibit different compressibility factor behavior than do sweet gases. Wichert and Aziz & Carr-Kobayashi and Burrows developed a simple procedure to account for these differences and adjust the pseudo-critical properties of natural gases. During this study, I observe that pseudo-critical temperature decreases if the mole percent of N2 increase. While, pseudo-critical pressure was increase with increasing the percentage of nitrogen. Also, the z factor increases with increasing pseudo- reduce pressure and temperature. In addition, pseudo-critical temperature decreases if the mole percent of H2S increase. I also notice that when I calculate the z-factor for reservoirs which contain C7+ by Stewart Mixing Rules and Kay’s there are some deviation on z factor between two methods but it reduce when I used the correction method for non-hydrocarbon and it is recommended to use Stewart Mixing Rules to investigate the impact of non-hydrocarbon impurities on natural gas properties.
None.
The author declares no conflict of interest.

©2017 Hamada. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.