Groundnut husk (GH) was used as an adsorbent to remove Mn²⁺, Zn²⁺ and Pb²⁺ ions from fertilizer industrial wastewater. FTIR-spectrum shows the participation of aromatic compounds (C=C), Aldehydes (C=O) and Alkenes (C=C) in adsorption due to their absence in the adsorbent after the process. Batch adsorption experiments were conducted to examine the effect of adsorbent mass, pH and contact time on adsorption of Mn²⁺, Zn²⁺ and Pb²⁺ from fertilizer industrial waste water. The results showed that Mn²⁺, Pb²⁺ and Zn²⁺ attained maximum percentage removal of 61.62%, 99.93% and 100% at adsorbent dose of 50g, 60g and 20g respectively. However the maximum percentage removal of Mn²⁺ and Pb²⁺ was achieved at pH 6 for 80min. while that of Zn²⁺ was achieved at pH 3 for 60min. Langmuir biosorption isotherm provided the best fit for sorption of Mn²⁺ and Pb²⁺ using groundnut husk as indicated by their correlation coefficient ($R^2$ ) of 0.558 and 0.441 hence the process was based on a physisorption mechanism. The kinetic studies showed that the biosorption process followed the pseudo-second order reaction order. This study has demonstrated that groundnut husk can be efficiently used as low cost alternative adsorbent for remediation of Mn²⁺, Zn²⁺ and Pb²⁺ from heavy metals contaminated wastewater.

Keywords: groundnut husk, heavy metals, biosorption, adsorption isotherm, kinetic models, wastewater

GH, groundnut husk; FTIR, fourier transformed infrared spectroscopy; AWBs, agricultural waste biomass; PAC, powder activated carbon

Pollution of the environment with toxic substances in waste water effluents is a major concern for human health and environmental quality, with heavy metals being one of the most dangerous pollutants. It has been reported that the toxicity due to metallic discharges into the environment far exceeds the combined total toxicity of all radioactive and organic waste.¹ Although small amounts of many heavy metals are necessary in normal biological cycles, most become toxic at high concentrations. Heavy metals are toxic to living organisms because they tend to persist in the environment, as they are non biodegradable and bio-accumulate, becoming concentrated in the food chain.² Metals such as lead, nickel, cadmium, manganese, chromium, cop-per, mercury and zinc are known to be significantly toxic.³ Manganese in particular is considered a pollutant mainly because of its organoleptic properties; in high concentrations, it causes neurological disorders.² High concentrations of nickel cause serious health effects, including liver and heart damage, skin irritation, nasal cancer, headache and dermatitis.¹ Consequently, the treatment of heavy metal contaminated waste water remains a topic of global concern since waste water collected from municipalities, communities and industries must ultimately be returned to receiving waters or to the land.³ Conventional treatment methods, have been found to be very expensive and difficult to maintain due to high capital and operational costs.^4,5 and also results to the generation of chemical sludge/secondary waste that must be treated before disposal as it also poses hazards and pollution risks to the environment.⁶ These challenges associated with conventional methods, have triggered interest and research for more efficient and eco-friendly heavy metal treatment methods.

Biosorption is a physiochemical process that occurs naturally in certain biomass which allows it to passively concentrate and bind contaminants onto its cellular structure.⁷ Pollutants interact naturally with biological systems through various routes, if not properly managed; these pollutants may seep into any biological entity within the range of exposure. The most problematic contaminants include heavy metals, pesticides and other organic compounds which can be toxic to wildlife and humans even at small concentration. Occurrence of heavy metals in our environment causes adverse effects on flora, fauna and also results to contamination of groundwater through leaching.⁸ Industrial wastes are waste generated by industrial activity which includes any material that is rendered useless during a manufacturing process such as that of factories, mills and mines. Some examples of industrial waste include; chemical solvents, paints, sand paper, paper products, industrial by-products, metals and radioactive wastes most of which are indiscriminately disposed in the environment in form of sewage and wastewater without treatment.^8,9

The increased biomass level of groundnut husk (GH) in the environment through dumping as a refuge due to high consumption rates of these agricultural products has become an environmental concerned due to their land space occupation and subsequent pollution problems. Hence the need for the recycling of this agro-waste for use as adsorbent in treatment of heavy metal contaminated wastewater. This will not only be economical but will also help to maintain the quality of the environment. This agricultural wastes is a promising clean up agents that could be harnessed and utilized for treatment of heavy metal contaminated wastewater due to their availability, potential cost-effectiveness, metal biding potential, non-hazardous nature and ease of disposed by incineration.^10,11 This research article focused on investigating the potential of groundnut husk agro waste in biosorption of heavy metals from fertilizer industrial wastewater.

Preparation of biosorbent

Groundnut husk used as biosorbent in this study was obtained from a local farm at Samaru, Zaria, Kaduna State, Nigeria. The groundnut husk was identified at the herbarium in the Department of Biological Science Ahmadu Bello University Zaria. The husk was washed with Acetone and boiled with deionised water for 30 minutes, dried, pulverized then stored in well coked containers.

Effects of different experimental factors on biosorption

Effect of adsorbent mass: Varying masses of the biosorbent (20-70g) were added in different conical flasks containing 1 liter of waste water, corked and agitated in a magnetic stirrer for 1hr at a speed of 100 rpm at room temperature. The content of each flask was filtered and analyzed using AAS.

Effect of pH: Exactly 1L of waste water was measured into different conical flask and 30g of the biosorbent was added and agitated at 100 rpm for one hour over a pH range of 3-8. The pH was adjusted using Hydrochloric Acid and Sodium hydroxide. Content of each flask was filtered and analyzed using AAS.

Effect of contact time: The effect of contact time on removal of metal ions was studied. The Adsorbent was added to different conical flask containing 1L of wastewater; the flask was closed and placed in a magnetic stirrer and agitated at 100 rpm for each of the contact time (20-120min). The content of each flask was then filtered and analyzed with AAS.

Determination of percentage metal sorption by activated carbon

20g and 30g of activated carbon (standard synthetic adsorbent used in industries) were weighed and added in a conical flask containing 1L of waste water separately, corked and agitated in a magnetic stirrer for 1hr at a speed of 100 rpm at RT. The content of the flask was then filtered and analyzed using AAS.

Heavy metal determination and analysis of adsorbent

Concentrations Zinc (Zn), Lead (Pb) and Manganese (Mn) in fertilizer wastewater were analyzed before and after treatment. Fourier Transformed Infrared Spectroscopy (FTIR) was carried out to identify the presence of functional groups.

Batch adsorption experiments

Batch adsorption experiment was conducted according to the methods described by Tichaona et al.¹² and Dawodu et al.¹³ by mixing biosorbents with fertilizer industrial waste water containing heavy metal ions in a 1L conical flask. The conical flask was corked and agitated in a magnetic stirrer for 1hr at a speed of 100 rpm at RT. The amount of biosorption was calculated based on the difference between the initial and final concentration ($C_e$ , mg/L) in every flask as follows:

$q_e=\frac{\left(C_o–C_e\right)V}{M}$ (1)

$q_t=\frac{\left(C_o–C_t\right)V}{M}$ (2)

$R\left(\%\right)=\frac{\left(C_o–C_t\right)x100}{C_o}$ (3)

Where
$q_e$ and $q_t$ = Amount of metal ions adsorbed (mg/g) at equilibrium and at time ‘t’ respectively
$C_o$ and $C_t$ = Initial concentration (at t =0) and its concentration at time t = t (mg/L)
M= Mass of adsorbents (g)
V= Volume of metal ions (L)
R= Percentage of metal ions removed. All experiments were carried out in duplicate and the result was presented as mean ± standard deviation.

Fourier transform infra-red spectroscopy (FTIR) analysis

Characterization of the biosorbent before use for biosorption process is necessary, to determine its suitability. The FTIR spectra analysis was utilized to identify the functional groups of groundnut husk powder before and after use in adsorption of heavy metal ions. The results of FTIR peak values and functional groups of groundnut husk powder before and after sorption are shown in Figure 1 below. The figures show the peak values and functional groups of groundnut husk powder before and after use. The IR-spectrum shows the presence of Alkyl halides (R-I), Alkenes (=C-H), Aromatic compound mono substituted (C-H), Alcohols (C-O), Alkyl halides (C-F), Ethers (=C-O-C), Alkanes and Alkyls (C-H), Aromatic Compounds (C=C), Amides (N-H), Alkenes (C=C), Aldehydes (C=O), Esters (C=O), Carboxylic acids (O-H) for groundnut husk powder while the used groundnut husk powder shows the absence of Aromatic Compounds (C=C), Aldehydes (C=O), Alkenes (C=C) signifying that this groups are major active sites for the binding of positively charged ions during biosorption and have participated in the biosorption of the heavy metals.¹³ Similar spectra were obtained for biosorption studies of metal ions using groundnut hull,¹⁴ cashew nut shells¹⁵ and palm nut shells.¹⁶

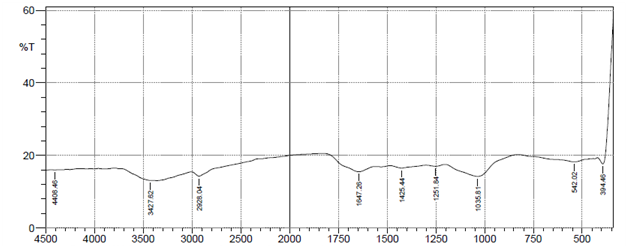
Plate A Before metal ions adsorption.

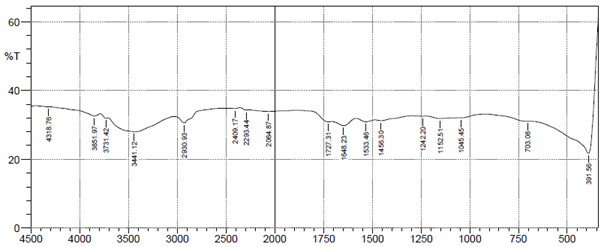
Plat B After metal adsorption.

Figure 1 FTIR spectrum of groundnut husk and used groundnut husk showing fragment peaks.

Effect of adsorbent mass on removal of metal ions

Figure 2 shows that increased adsorbent loading increased the metal ions percentage removal. Manganese attained maximum removal at 50g with 61.62% removal, Lead attained maximum removal at 60g with 99.93% removal while Zinc attained a 100% removal using 20g of groundnut husk powder as adsorbent further increase in mass of the adsorbent brought no change in adsorption of zinc. The percentage removal of Mn(II), Zn(II) and Pb(II) ions in this study, increased with increasing dosage due mainly to an increase in the number of available exchangeable active sites for metal ion sorption.¹⁷

Effect of pH on removal of metal ions

From Figure 3, it was observed that an increase in pH of fertilizer wastewater resulted to an increase in the percentage removal of metal ions. A maximum removal was attained for Manganese at pH 6 with 69.01% removal, Lead had a maximum removal of 97.66% at pH 6 while 100% removal of zinc was attained at low pH of 3 and no further change in zinc adsorption was observed with increase in pH of wastewater using groundnut husk powder as adsorbent. It was observed that at low pH, higher concentration and mobility of H⁺ ions favor H⁺ sorption compared to metal ions; this creates a competition between the protons and metal ions for the active sites of the biosorbent. According to Onundi et al.¹⁶ metal ions are more soluble in solution at lower pH values thus reducing their sorption. Hence the low sorption at low pH in this study was thus due to saturation of the active sites of groundnut husk with hydrogen ions. However, an initial metal sorption observed with increase in pH was due to a decrease in competition between hydrogen ions and metal ions for the biosorbents surface binding sites and also due to decrease in positive surface charge, which resulted in less electrostatic repulsion between the surface and metal ions before ion exchange which is the major mechanism of metal uptake.¹⁷ As the pH of the solution increases, more negatively charged surface becomes available thus facilitating greater metal biosorption. Similar tendencies were found in biosorption processes using diverse agricultural waste biomass (AWBs). Giri et al.¹⁸ reported a similar trend on studies of the effect of pH on the removal of Cr(VI) using Eichhornia crassipes root activated carbon. However, at higher pH 7 and 8 metal ions tend to precipitate out of solution. Therefore the removal of metal ions at higher pH values is due to the formation of metal ion precipitates rather than sorption.¹⁹

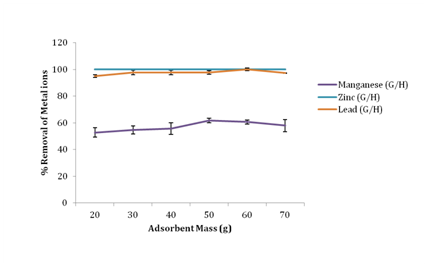
Figure 2 Effect of adsorbent mass on percentage removal of metal ions.

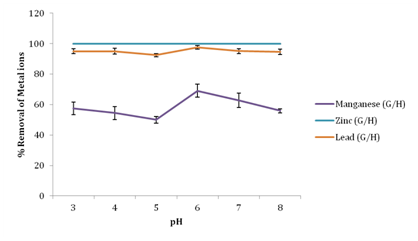
Figure 3 Effect of pH on percentage removal of metal ions.

Effect of particle size on metal ion removal

Figure 4 shows the effect of particle size on adsorption of metal ions from waste water using groundnut husk powder as adsorbents. It was observed that with decrease in particle size, the percentage removal of metal ions increases. At 0.5mm particle size, zinc, lead and manganese had maximum removal of 99.23%, 95.12% and 61.79% respectively. Increasing particle size from 0.5mm to 2mm resulted to a decrease in percentage removal of metal ions. Manganese adsorption decreased from 52.76% to 54.89% as adsorbent as the particle size increased from 0.5mm to 2mm. While percentage removal of zinc decreased from 99.23% to 79.71% and 95.12% to 82.85% for lead as the particle size increases from 0.5mm to 2mm. The particle size of a biosorbent has a tremendous effect on the biosorption process.¹⁷ The increase in the percentage removal of manganese, lead and zinc ions with decreasing biosorbent particle size in this study is attributable to a decrease in the surface area of biosorbent available for metal ions binding. The breaking up of larger particles into smaller ones tends to open tiny cracks and channels on the particle surface of the biosorbent, resulting in greater accessibility and better diffusion of the metal ions.¹³ Similar results have been reported previously.^1,20,21

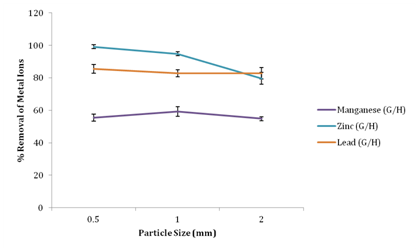
Figure 4 Eeffect of particle size of adsorbents on percentage removal of metal ions.

Effect of contact time on metal ion removal

In this study, the percentage metal ion removal approached equilibrium within 80 minutes for manganese, 80 minutes for zinc and 60 minutes for lead, with manganese, Zinc and lead recording a percentage removal of 62.48%, 100% and 97.60% respectively. Hence following a percentage removal trend of Zn²⁺> Pb2+> Mn²⁺. This experiment shows that different metal ions attained equilibrium at different times. The removal rate of metal ions also increases with an increase in contact time. The rate of biosorption is higher at the early stage, due to a large available surface area of the biosorbent and presence of abundant active sites on the surface. The fast initial uptake is also due to the rapid accumulation of the heavy metal ions on the surface of the biosorbent. As these sites become exhausted or saturated with time, the sorption rate also decreases.²¹ The faster removal rate with Zn(II) than with Pb(II) and Mn(II) may be due to the smaller ionic radius of Zn(II) than Pb(II) and Mn(II), which makes for easier and more rapid diffusion to the surface of Groundnut husk¹³ (Figure 5).

Figure 5 Effect of contact time on percentage removal of metal ions.

Effect of removal of metal ions by activated carbon vis-à-vis adsorbents

Figure 6 shows the percentage removal of metal ions by groundnut husk (GH) powder and activated carbon (standard adsorbent used in industries). At 20g of adsorbents there was 82.92% and 52.76% percentage removal of manganese using activated carbon and groundnut husk powders as adsorbent respectively. At 30g of adsorbents there was 54.74% removal of manganese with groundnut husk powder and 88.81% removal with activated carbon as adsorbent. At 30g of adsorbent used, percentage removal of lead was 99.75% using groundnut husk powder and 99.81% with activated carbon as adsorbent, while groundnut husk had 100% removal for zinc at both 20g and 30g of adsorbent. Activated carbon had 92.83% and 100% removal for zinc at 20g and 30g respectively. The results from this study have revealed that industrial Powder Activated Carbon (PAC) is a more potent adsorbent for reducing heavy metals from fertilizer industrial wastewater. Activated carbon had a better adsorption capacity for metal ions than groundnut husk powder but the percentage difference was not significant. This could possibly be due to the presence a larger surface area on activated carbon, available for metal ions binding.¹³

Adsorption isotherms

An adsorption isotherm model gives the equilibrium relationship between the sorbate (metal ion) in the fluid phase (solution) and the sorbate sorbed on the sorbent (adsorbent) at constant temperature.^22,23 They are very useful for obtaining the adsorption capacity so as to facilitate the evaluation of the feasibility of the adsorption process for a given application and for selection of the most appropriate sorbent at the optimum experimental conditions.²² In this work, the Langmuir and freundlich isotherm models were employed to interpret the sorption process in order to understand the mechanism of metal ions adsorption on groundnut husk powder. The experimental data were fitted to therefore mention equilibrium isotherm models. Langmuir biosorption isotherm gave the best fit for sorption of metal ions using groundnut husk as indicated by their correlation coefficient which were higher than that of the freundlich isotherm (Table 1). The Langmuir equation .²⁴ is given as:

$q_e=\frac{q_m{k}_a{c}_e}{1+k_a{c}_e}$ (4)

 Where
$q_e$ = Amount of metal ions adsorbed per unit mass at equilibrium (mg/g)
$q_m$ = Maximum possible amount of metal ions that can be adsorbed per unit mass of adsorbent (mg/g)
${}_e$ = Concentration of sorbate (in solution at equilibrium (mg/l)
$K_a$ = Sorption equilibrium constant

The linearised form of equation is

$\frac{C_e}{q_e}=\frac{1}{k_a{q}_m}+\frac{C_e}{q_m}$ (5)

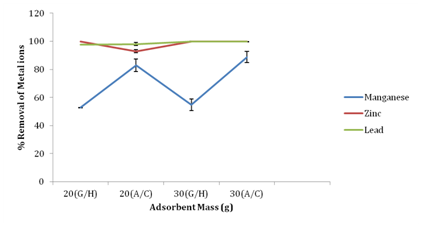
Figure 6 Percentage removal of metal ions by activated carbon a standard adsorbent vis-a-vis adsorbents (Groundnut Husk Powder).

A plot of $\frac{C_e}{q_e}$  versus $C_e$  gives a straight line, with a slope of $\frac{1}{q_m}$  and intercept $\frac{1}{K_a{q}_m}$  The essential characteristics of Langmuir isotherm can be expressed in terms of a dimensionless constant $K_R$ , the separation factor or equilibrium parameter, which is defined as:

$K_R=\frac{1}{1 +K_a{C}_o}$ (6)

Where
$K_R$ = Dimension less separation factor
$K_a$ = Langmuir constant (L/mg)
$C_0$ = The initial concentration of metal ions (mg/L).

The shape of the isotherm is linear if $K_R$ =1, it is irreversible if $K_R$ <0, unfavourable if $K_R$ >1 and favourable if 0<$K_R$ < 1.²⁵ The values of $K_L$ (L/mg) were fairly low (Table 2) which implies low surface energy in the process and consequently low bonding between metal ions and biosorbent indicating a physisorption mechanism, marking recovery of the metal ions through desorption easy.²⁵ This is a major criterion in selecting a biosorbent.²⁴ The Freundlich isotherm is an empirical model which indicates the surface heterogeneity of the adsorbent. The equation is given as:

$q_e=K_f{C}_e{}^{1/n}$  (7)

The linear form of the equation is:

$og{q}_e=log{k}_f+\frac{1}{n}log{c}_e$ (8)

Adsorption kinetics

The study of the adsorption kinetics of a sorption process is very important as it describes the rate of adsorbate uptake, which in turn evidently controls the residence time of the solute uptake at the solid-solution interface or the sorption reaction.^26-28 It is an important characteristic in defining the efficiency of sorption.²⁶ The data obtained from the study of adsorption dynamics are necessary to understand the variables that affect the sorption of solutes and the rate of sorption observed can also be used to develop predictive models for column experiments.²⁸ The most important thing when searching for an appropriate sorption mechanism, therefore, is to choose a mathematical model which not only fits the data with satisfactory accuracy but also complies with a reasonable sorption mechanism.²⁹ Generally, sorption of adsorbate by an adsorbent consists of several steps which include:

1. Transport of sorbate (solute) from the solution to the film surrounding the sorbent particles. This is called bulk diffusion.
2. Diffusion of the sorbate from the film to the external surface (external diffusion)
3. Diffusion from the surface to the internal sites i.e. intra-particle transport within the particle.
4. Sorption of the sorbate on the interior surface of the sorbent (i.e. pore diffusion). This can involve several mechanisms including reaction kinetics at phase boundaries.^27,29,30

Various kinetic models have been proposed and used to study and describe the mechanism of a Solute uptake by an adsorbent from aqueous solution.²⁹ In this study, however, the kinetic equations employed to investigate the mechanism of metal ions adsorption are:

The Pseudo-first order by Lagergren³¹ given as:

$\frac{d_q}{d_t}=k_1\left(q_e-q_t\right)$ (9)

Where
$q_e$ and$q_t$ = The adsorption capacities at equilibrium and at time t (mg/g) respectively
$k_1$ = Rate constant of pseudo-first order adsorption (min-1)
After integration and applying boundary conditions t= 0, to t= t and $q_t$ = 0 to $q_t=q_e$  equation (9) becomes

Where
$q_e$ and$q_t$ = The adsorption capacities at equilibrium and at time t (mg/g) respectively
$k_1$ = Rate constant of pseudo-first order adsorption (min-1)
After integration and applying boundary conditions t= 0, to t= t and $q_t$ = 0 to $q_t=q_e$  equation (9) becomes

$\frac{d_q}{d_t}=k_1\left(q_e-q_t\right)$ (10)

Where
$q_e$ (mg g^-1)= The amount of metal ions adsorbed at equilibrium
$q_t$ (mg g^-1)= The amount of metal ions adsorbed at time t
$k_1$ (min-1)= The rate constant of pseudo-first order adsorption
A plot of $\left(q_e–q_t\right)$  versus t gives the slope =$k_1$  and intercept=$log{q}_e$
The Lagergren first order rate constant ($k_1$ ) and $q_e$  determined from the model for the metals and their respective coefficients of correlation,$R^2$ , are shown in Table 2. The Pseudo-second order equation.³² is given as:

$\frac{d_q}{d_t}=k_2{\left(q_e-q_t\right)}^2$ (11)

Where $k_2$ are the rate constant of pseudo-second order adsorption (g mg^-1 min-1) and other symbols have their usual meanings. After integration, equation (12) becomes:

$\frac{1}{q_e-q_t}=\frac{1}{q_e}+k_2$ (12)

 Equation (12) is linearised to give:

$\frac{t}{q_t}=\frac{1q_e^2}{k_2}+\frac{\left(1\right)t}{q_e}$ (13)

$k_{2}q{e}^2=h$ (14)

Combining equations (13) and (14) gives

$\frac{t}{q_t}=\frac{1}{h}+\frac{\left(1\right)t}{q_e}$ (15)

A plot of $\frac{t}{q_t}$ verses t gives a straight line. If the sorption process follows pseudo-second order, h, is described as the initial rate constant as t approaches zero. The correlation coefficients and adsorption capacities calculated from the kinetics models employed in the interpretation of the experimental data are given in Table 2. The pseudo-second order kinetic model which is based on the assumption that chemisorption is the rate determining step, provided a good fit to the experimental data as can be seen from the very high linear regression($R^2$ ) values (Table 2). Several studies have also reported high regression ($R^2$ ) values for this model.^1,20,33.

The potential of modified groundnut husk for the removal of Mn(II), Zn(II) and Pb(II) ions from aqueous solution in this study was dependent on biosorption experimental factors such as pH, biosorbent dose and contact time. The Langmuir biosorption isotherm gave the best fit for the biosorption of Mn(II), Zn(II) and Pb(II) ions onto GH powder through majorly the physisorption mechanism. The kinetic result shows that the biosorption process followed pseudo-second order reaction. This study has shown that GH has a considerable high removal percentage, this can be explored for use as an alternative adsorbent for the treatment of waste water contaminated by Mn(II), Zn(II) and Pb(II) ions.

None.

The author declares no conflict of interest.

1. Badmus MAO, Audu TOK, Anyata BU. Removal of lead ion from industrial wastewaters by activated carbon prepared from periwinkle shells. Turkish J Eng Env Sci. 2007;31(2007):251–263.
2. Singh R, Gautam N, Mishra A, et al. Heavy metals and living systems: an overview. Indian J Pharmacol. 2011;43(3):246–253.
3. Barka N, Abdennouri M, El Makhfouk M, et al. Biosorption characteristics of cadmium and lead onto eco-friendly driedcactus cladodes. Journal of Environmental Chemical Engineering. 2013;1(3):144–149.
4. Rangel VMM, Martínez RC, Villanueva RA, et al. As(V) biosorption in an aqueous solution using chemically treated lemon (Citrus aurantifoliaswingle) residues. J Food Sci. 2012;77(1):T10–T14.
5. Mishra V, Balomajumder C, Agarwal VK. Kinetics, mechanistic and thermodynamics of Zn(II) ion sorption: a modeling approach. Clean Soil Air Water. 2012;40(7):718–727.  
6. Kumar U. Agricultural products and by-products as a low-cost adsorbent for sequestering heavy metal ions from aqueous solutions: A review. Bioresource Technology. 2006;99(14):65–90.
7. Volesky B, Bohumil. Biosorption and biosorbents. In: Volesky B editor. Biosorption of heavy metals. CRC Press, Florida, USA: Boca Raton; 1990. p. 3–5.
8. Tatah S, Ogodo AC, Kaa LC, et al. The potential use of Alternaria alternate in bioremediation of wastewater contaminated by hexavalent chromium ion. FUW Trends in Science & Technology Journal. 2016;1(1):115–118.
9. Maczulak AE. Pollution: Treating Environmental Toxins. New York, USA: Info base Publishing; 2010. 120 p.
10. Okeke EC, Eze C. Nutrient composition and nutritive cost of Igbo traditional vendor foods and recipes commonly eaten in Nsukka. Journal of Agriculture, Food, Environment and Extension. 2006;5(1):36–44.
11. Baryeh EA. Physical properties of bambara groundnuts. Journal of Food Engineering. 2001;47(4):321–326.
12. Tichaona N, Maria MN, Emaculate M, et al. Isotherm study of the biosorption Of Cu (II) From Aqueous Solution By Vigna Subterranea(L.) VerdcHull. Journal of Scientific & Technology Research. 2013;2(4):119–206.
13. Dawodu FA, Akpomie KG. Simultaneous adsorption of Ni(II) and Mn(II) ions from aqueous solution unto a Nigerian kaolinite clay. Journal of Materials Research and Technology. 2014;3(2):129–141.
14. Qaiser S, Saleemi AR, Umar M. Biosorption of lead (II) and chromium (VI) on groundnut hull: Equilibrium, kinetics and thermodynamics study. Electronic Journal of Biotechnology. 2009;12(4):1–4.
15. Tangjuank S, Insuk N, Tontrakoon J, et al. Adsorption of lead (II) and cadmium(II) ions from aqueous solutions by adsorption on activated carbon prepared from cashew nut shells. Proceedings of World Academy of Science: Engineering & Technolog. 2009;6(2):298–306.
16. Onundi YB, Mamun AA, Khatib MFA, et al. Adsorption of copper, nickel and lead ions from synthetic semiconductor industrial wastewater by palm shell activated carbon. Int J Environ Sci Technol. 2010;7(4):751–758.
17. Guler UA, Sarioglu M. Single and binary biosorption of Cu(II), Ni(II) and methylene blue by raw and pretreated Spirogyriasp: equilibrium and kinetic modeling. Journal of Environmental Chemical Engineering. 2013;1(3):369–377.
18. Giri, Anil Kumar, Patel, Rajkishore, et al. Removal of Cr(vi) from aqueous solution by Eichhornia crassipes root biomass-derived activated carbon. AGRIS. 2012;185-186:71–81.
19. Gautam RK, Mudhoo A, Lofrano G, et al. Biomass derived biosorbents for metal ions sequestration: adsorbent modification and activation methods and adsorbent regeneration. Journal of Environmental Chemical Engineering. 2014;2(1):239–259.
20. Das B, Mondal NK. Calcareous soil as a new adsorbent to remove lead from aqueous solution: Equilibrium, kinetic and thermodynamic study. Universal Journal of Environmental Research and Technology. 2011;1(4):515–530.
21. Barka N, Abdennouri M, El Makhfouk M, et al. Biosorption characteristics of cadmium and lead onto eco-friendly dried cactus cladodes. Journal of Environmental Chemical Engineering. 2013;1(3):144–149.
22. Dinçer AR, Güneş Y, Karakaya N, et al. Comparison of activated carbon and bottom ash for removal of reactive dye from aqueous solution. Bioresour Technol. 2007;98(4):834–839.
23. Sathishkumar M, Jung SH, Song SH, et al. A novel method in utilization of bok bunja seed wastes from wineries in liquid-phase sequestration of reactive blue 4. Int J Environ Res. 2009;3(1):1–12.
24. Ho YS, Chiang TH, Hsueh YM. Removal of basic dye from aqueous solution using tree fern as a biosorbent. Agris. 2005;40(1):119–124.
25. Huang K, Zhu H. Removal of Pb (II) from aqueous solution by adsorption on chemically modified muskmelon peel. Environ Sci Pollut Res Int. 2013;20(7):4424–4434.
26. Arivoli S, Henkuzhali M. Kinetics, mechanistic, thermodynamic and equilibrium studies on the adsorption of rhodamine B by acid activated low cost carbon. E-Journal of Chemistry. 2008;5(2):187–200.
27. Igwe JC, Abia AA, Asuquo ED. Studies on the influence of counter ions and modification of adsorbent on the kinetics of Hg(II), As(III) and Pb(II) ions removal from aqueous solutions using Sawdust Meal. Journal Chem Soc Nigeria. 2012;37(2):77–79.
28. Oladoja NA, Asia IO, Aboluwoye CO, et al. Studies on the sorption of basic dye by rubber (Hevea brasiliensis) seed shell. Turkish J Eng Env Sci. 2008;32:143–152.
29. Yang X, Cui X. Adsorption characteristics of Pb(II) on alkali treated tea residue. Water Resources and Industry. 2013;3:1–10.
30. Malarvizhi R, Sulochana N. Sorption isotherm and kinetic studies of methylene blue uptake onto activated carbon prepared from wood apple shell. Journal of Environmental Protection Science. 2008;2:40–46.
31. Langmuir I. The Adsorption of gases on plane surfaces of glass, mica and platinum. J Am Chem Soc. 1918;40(9):1361–1403.
32. Ho YS, Mckay G. A comparism of chemisorptions kinetic models applied to pollutant removal on various sorbents. Process safety and environmental protection. 1998;76(B4):332–340.
33. Liang S, Guo X, Feng N, et al. Adsorption of Cu(II) and Cd(II) from aqueous solution by mercapto-acetic acid modified orange peel. Colloids Surf B Biointerfaces. 2009;73(1):10–14.