Human biofield components explained: a tensegrity-based biophysical framework for energy medicine

doi:10.15406/ijcam.2025.18.00731

International Journal of

eISSN: 2381-1803

Complementary & Alternative Medicine

Review Article Volume 18 Issue 2

Human biofield components explained: a tensegrity-based biophysical framework for energy medicine

Rick Sá^1,2

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

¹National Institute of Applied Naturopathy, Rio Grande do Sul, Brazil
²Saint Thomas Aquinas University, Florida, USA

Correspondence: Rick Sá, National Institute of Applied Naturopathy, Vila Rosa, Novo Hamburgo - 93315-040; RS, Brazil

Received: March 25, 2025 | Published: April 10, 2025

Citation: Sá R. Human biofield components explained: a tensegrity-based biophysical framework for energy medicine. Int J Complement Alt Med. 2025;18(2):77-85. DOI: 10.15406/ijcam.2025.18.00731

Download PDF

Abstract

There is a growing demand for integrative and complementary therapies for various health conditions, while the mechanisms and biological pathways for some of these therapies are poorly explored. In particular, bioelectric, biomagnetic and anthropogenic fields interact with biological structures such as tissues, cells and DNA. It is suggested that these interactions may create an integrated system of internal communication, with the potential to promote therapeutic benefits. The theoretical model Biofield-Tissue Tensegrity Matrix (BTTM) is presented by combining concepts from physics, biology and medicine to serve as a possible theoretical basis for energy therapies.

Keywords: bioelectromagnetic field, biofield, cellular communication, energy therapy, energy medicine

Introduction

In recent decades, scientific advances have provided a deeper understanding of the energetic properties of living systems, beyond biochemistry, expanding the theoretical bases of biology and conventional medicine. Biophysics researchers have shown that the evolutionary process of living beings is governed by an omnipresent electromagnetic potential,^1–3 which reinforces the concept of electromagnetic force as a product of one of the four known fundamental interactions. In mainstream medicine, biological systems are described from a biochemical perspective, where enzymes, proteins and other molecules interact in a seemingly chaotic manner within cells, performing vital functions through random collisions.^4,5 However, this mechanistic view of a disorganized “soup” of biomolecules in suspension has been revisited, especially with the discovery of electromagnetic fields generated by cellular structures and processes described in biophysics.

In the early 20th century, the discovery that organs produce measurable electrical fields on the surface of the human body led to the development of diagnostic tools such as the electrocardiogram (ECG) and the electroencephalogram (EEG).⁶ These technologies revolutionized medical diagnosis by allowing the observation of cardiac and brain electrical activity. However, these signals represent only a fraction of the body's bioelectrical activity. Subsequent research revealed that, in addition to electrical fields, living tissues also generate magnetic fields associated with the flow of ions and intracellular currents. Initially considered insignificant, these biomagnetic fields are now recognized as sensitive indicators of the organism's physiological activities.^7,8

Advances in measurement technology, such as the magnetoencephalogram (MEG) and the SQUID (Superconducting Quantum Interference Device), have enabled the detection of magnetic fields emitted by the brain and other tissues, overcoming limitations of conventional electrical methods.^9,10 Unlike electrical signals, which are attenuated when passing through layers of skin and skull, magnetic fields pass through these tissues without significant distortion, providing a more accurate view of internal processes.¹¹ These discoveries have paved the way for a more integrated and coherent understanding of the energy fields surrounding the human body, often referred to as the human biofield.

A definition of the human biofield as a field that is not necessarily electromagnetic has been proposed,¹² supposedly due to the understandable uncertainties of science about its nature. However, a broad basis for understanding the “physiology of the biofield” has been published, dealing with an interdisciplinary approach and offering a general description of endogenous, electric and magnetic fields, and their role in physiological regulation and health, in addition to proposing the physiology of the biofield as a new scientific discipline.¹³ Complementarily, from a biophysical perspective, the hypothesis of a tissue tensegrity matrix has been explored, in which vibrational information can be transmitted through an interconnected network, which acts as a coupled harmonic oscillator, allowing the transfer of energy and signaling from the cell periphery to the nucleus and, finally, to the DNA.¹⁴ Oschman, influenced by the hypothesis of an integrated tissue tensegrity matrix, called it a living matrix, an interface between endogenous processes and the external environment:

“The common denominator in all natural therapeutic approaches is a living matrix that is exquisitely designed to absorb the information encoded in different types of vibrational energy and convert them into signals that are easily transmitted through the continuous tensegrity semiconductor living matrix.”¹⁵

Considering that Oschman's living matrix is the human biofield, also tends to associate it with a living entity, interconnected with the whole (internal and external) by a continuum. Thus, both its physiology and the tensegrity of bioelectromagnetic components that constitute it should be subject to analysis. The present work aims to 1) review and discuss the main bioelectromagnetic components of the human biofield, addressing their functions and possible mechanisms of interaction; 2) propose the constitution of an interactome model in the Biofield-Tissue Tensegrity Matrix (BTTM) operated by the human biofield.

Bioelectromagnetic components of the human biofield

First of all, it is proposed that bioelectromagnetic components refer to the set of biological structures and processes that exhibit electrical and magnetic properties, both endogenous and exogenous, functioning as conductors, semiconductors, generators, organizers and resonators, which can be measured and analyzed by classical methods of physics and chemistry. These components include elements that generate or conduct electricity and magnetism in the body, such as blood plasma, minerals, and tissues, etc.

A clear and organized definition of the components of the human biofield is essential for the concept to transcend abstraction and become a practical tool for research and clinical application. By categorizing the components and detailing their mechanisms of interaction, a nomenclature and functional structure are proposed that facilitate both academic study and future clinical implementation. This approach provides an organized knowledge base that aids in the replication of studies and the standardization of practices, enabling the biofield to be discussed and applied in an objective and operational manner. Thus, the human biofield begins to be seen as an interconnected and measurable system, aligned with scientific standards and prepared for integration into health practices.

Conductors, semiconductors and generators

It is believed that since the dawn of life, natural electromagnetic fields have acted as bioelectric “skeletons,” shaping cellular structure and organization in a continuum toward the development of more complex multicellular systems.¹⁶ Bioelectric fields tend to be subordinate to the “Principle of Fertile Evolution”, which describes how the use of free energy brings significance to a more evolved configuration of matter.^17–19 Therefore, bioelectric fields are considered structural and functional “foundations” in living organisms, highlighting their importance in the configuration of the human biofield.

The discovery of biological electricity dates back to the work of Willem Einthoven in the early 20th century. He recorded the electricity generated by the heart using a sensitive galvanometer, laying the foundation for the electrocardiogram (ECG) and the understanding of bioelectric currents that spread through tissues and the circulatory system, due to the high salt content of blood, which acts as an excellent electrical conductor.⁶ The concept of “biological electricity” refers to the flow of charged particles (such as sodium, potassium, and calcium ions) across cell membranes, which sustains vital functions and communicates bioelectrical information throughout the body.¹⁵

The article “Toward a New Biochemistry?” in the journal Science proposed that proteins in the human body have semiconductor properties.²⁰ It is interesting to note that some important protein and molecular structures, which are excellent electron conductors, have conformational models of overlapping filaments (spirals) or helical structures, such as the DNA molecule, myosin and actin filaments, keratin and collagen.^21,22 the latter being a superconductor when aligned with water molecules. This alignment facilitates the conduction of electrical charges and promotes a biophysical communication network that extends throughout the organism. This phenomenon, known as the “streaming effect”,^23,24 is fundamental to understanding signal transmission and the informational interactome of the human biofield.

Collagen, one of the most abundant proteins in the human body, has a triple helical structure that provides mechanical support and facilitates intercellular communication in connective tissues. In terms of its electrical and piezoelectric properties, collagen demonstrates unique proton conduction capabilities, especially when combined with water molecules structurally organized around its fibers. These water molecules form a network of “nanotubes” in which proton conduction occurs in a nearly superconductive manner, a process that allows rapid and efficient transport of electrical charges along the collagen fibers. Nafion films, for example, have a proton conductivity of approximately 0.1 S/cm, one of the highest in polymeric proton exchange membranes.²⁵

Biological water constitutes about 70% of the body mass in adults, 99% of the molar weight (of living organisms), 79% of the body mass of newborns and also reveals peculiar properties as an energy transducer.^26–28 Water that organizes around collagen fibers forms what is known as the Exclusion Zone (EZ), a highly structured and coherent region with properties distinct from free-flowing water.^29–31 This zone is essentially “excluded” from particles and ions, which creates an environment of high viscosity and conduction capacity, ideal for the propagation of electromagnetic and mechanical waves in the biofield. In addition, EZ water absorbs light around 270 nm and emits fluorescence, which reflects its coherent and ordered state. This behavior of EZ water aligns with the properties of piezoelectric materials, facilitating the conduction of bioelectric signals along the collagen matrix.²⁵

Liquid crystalline order properties, including nematic, smectic, and chiral phases, have been observed in cytoskeletal constructs in vitro and in subcellular filaments in vivo. These properties have been observed in various types of cellular tissues, suggesting that these phenomena may be common in human cells, especially in the way cells organize, interact, and respond to mechanical stimuli.³² Furthermore, the electromechanical behavior of biological materials, including organelles such as microtubules, mitochondria, nuclei, and cell membranes, have been analyzed, and their effective elastic (flexoelectric) and piezoelectric coefficients affect cellular behavior based on the structure, microtubule orientation, and direction of mechanical stress.³³

Furthermore, the piezoelectric effect—the generation of electric fields in response to compression or tension—plays a significant role in the physiology of bone and various tissues. Collagen in bone generates electrical potentials when subjected to mechanical stress, stimulating the activity of osteogenic cells, such as osteocytes, and facilitating bone adaptation according to Wolff's Law.^34–36 This mechanism is also observed in various tissues of the body, where piezoelectricity facilitates signal conduction and response to external stimuli, contributing to communication and maintenance of the biofield (Figure 1).

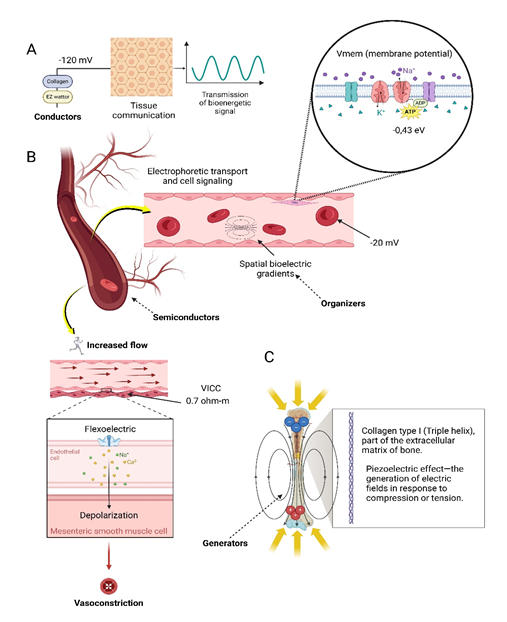
Figure 1 A. Conductors: Representation of biological tissues and fluids that act as conductors of electrical signals in the human body. Includes collagen and structured water (exclusion zone, EZ), with electrical potentials of up to -120 mV, essential for tissue communication and the transmission of bioenergetics signals; B. Semiconductors and Organizers: Biological tissues exhibit semiconductor properties that facilitate electrophoretic transport and cell signaling. Spatial bioelectric gradients are highlighted as fundamental organizers, with cell membrane potentials around -20 mV. Increased blood flow induces vasoconstriction mediated by piezoelectric effects and electrochemical signals in endothelial and smooth muscle cells, with vascular conductivity (VICC) of 0.7 ohm-m; C. Generators: Representation of the piezoelectric effect in bone tissue and blood vessels, where compression or tension generates electric fields, contributing to biological signaling and mechanical response. Blood vessels act as bioelectric generators in response to physical stimuli, integrating electrical and mechanical signals.

Regarding the mention of conductive and semiconductor components to the aforementioned piezoelectric effects, it is important to highlight that some of these bioelectromagnetic materials have triple functions: they are semiconductors, facilitating the flow of electricity, they are generators, transforming mechanical stimuli into electrical signals and they can be transmitters, sending information and interpreting it by the organism, as will be discussed in the Bioresonant or Transmitters subsection.

Organizers

The classical view of the cell as a “chemical soup” — a chaotic environment where biomolecules interact randomly — has been challenged by a perspective that considers living systems as self-organized, dynamic, and in a state of non-equilibrium. Biophotons play an essential catalytic function in biochemical reactions within cells, reinforcing their role as organizers and regulators in biological processes. Studies indicate that these ultra-weak light emissions, between 1 and 100 photons per second per square centimeter, are capable of triggering and regulating biochemical reactions, facilitating the transfer of information and energy in the organism. Despite having an extremely low intensity, these photons are able to transmit molecular signals that modulate enzymatic activities and directly influence the rate of oxidation and reduction of key molecules for cellular metabolism, suggesting that biophotons can act as an organizing field. The idea is that deviations in biophotonic emission patterns may signal regulatory dysfunctions associated with disease states, functioning as an internal communication network that organizes and coordinates cellular processes.^37,38 It is also suggested that biophoton production is related to oxidative metabolism in mitochondria and the generation of reactive oxygen species (ROS). In states of oxidative stress, which often accompany cardiovascular diseases, there is an increase in biophoton emissions, indicating metabolic imbalances and mitochondrial dysfunctions. Thus, biophotonic emissions can act as diagnostic tools to identify imbalances and assess cellular health, and may be useful in the diagnosis of cardiovascular diseases and diabetes mellitus.^39,40

Organizing components can also be evidenced in the observations of Nordestron, who highlights blood plasma as the main electrophoretic conductor within the so-called Vascular-Interstitial Closed Circuits (VICC), with a resistivity of 0.7 ohm-m. In situations of spontaneous polarization, such as in tissue injuries, a bioelectric gradient is generated that favors regeneration and potentially contributes to the destruction of tumor cells. These circuits, formed by the vessel walls and the interstitial fluid surrounding the cells, facilitate electrophoretic transport and cell signaling.^41,42 The role of membrane potentials and spatial bioelectric gradients—also known as morphogenetic gradients—in regulating cellular behavior and cancer pathogenesis is ongoing to be well established. These bioelectric gradients are essential for anatomical organization, tissue morphology, and processes such as wound healing and embryonic development.^43,44 Depolarization of the membrane potential, considered an indicator of tumorigenic potential, emphasizes the relevance of bioelectric and biophotonic gradients as organizers of the human biofield and promoters of cellular health.

Bioresonant or transmitters

Based on the principle of internal omnipresence of the functions of conductors, semiconductors, generators and organizers, as bioelectromagnetic components of the human biofield, the tensegrity between all parts of a whole is reasonably acceptable. Since the human biofield is seen as a living system that controls what is called here the biofield-tissue tensegrity matrix (BTTM) and tissue tensegrity matrix system as speculated by Pienta & Coffey,¹⁴ this matrix is attributed mechanical properties and a vibratory continuum, in which the parts have both structural and energetic elements that echo throughout the organism. The informational property of the human biofield can be explained by the Tissue Tensegrity-Matrix that, due to solid and aqueous state properties, produces piezoelectric and streaming effects, which resonate through waves, called phonons and solitons.

Phonons are quantizations of mechanical or acoustic vibrations that occur within crystalline or semi-crystalline structures.⁴⁵ In biology, this can be expanded to organized structures within cells and tissues, such as the cytoskeleton and collagen networks, which have a degree of coherent organization similar to that of a liquid crystal.³² They represent the transport of mechanical energy through these structures in the form of coordinated vibrations. Solitons are nonlinear waves that, unlike conventional waves, maintain their shape and energy over large distances.⁴⁶

The soliton can transport energy along the peptide molecule without dissipation, and there is a possibility that this energy can be transferred to adjacent materials, depending on factors such as energy coupling and structural conditions of the environment. If the soliton hits adjacent materials (such as other nearby molecules or structures), its energy can be transferred or coupled, depending on the scenario: a) The soliton can induce vibrations or excitations in nearby molecules, such as the cytoskeleton, cell membranes or even structured water molecules; b) The transfer will depend on physical proximity, continuity of the medium (e.g., interaction with protein networks), and structural alignment between the alpha-helix and adjacent materials; c) If there are similar vibrational frequencies between the soliton and adjacent materials, the energy can be transmitted efficiently (as in the case of vibrational resonance). This suggests that solitons can not only transport energy internally, but also act as intermediaries in biophysical communication.

The theoretical models of Davydov^47–52 and Pang^53,54 offer complementary explanations for the transport of biological energy in proteins, highlighting the roles of phonons and solitons in this process. Davydov proposed that the transport of biological energy in proteins occurs through solitons formed by nonlinear interactions between excitons (vibrational quanta) and structural deformations of the α-helical chains of proteins. In Davydov's model, the energy released by ATP hydrolysis is stored as vibrational excitations of the amide-I type, which interact nonlinearly with deformations of the α-helical chains of proteins, forming self-sustained solitons that transport energy along the chains. These solitons, by preventing the dispersion and dissipation of energy, ensure their efficiency in biological processes, such as muscle contraction and the transport of electrical pulses.

Total Hamiltonian in the Davydov Model. Represents the Hamiltonian of the system, with terms for excitons $H_{e x}$ , phonons $H_{p h}$ and your interactions $H_{i n t}$ :

\begin{array}{l} H = H_{e x} + H_{p h} + H_{int} = \sum_{n} [(\in_{0} - D) B_{n}^{+} B_{n} - J (B_{n}^{+} B_{n} + 1 + B_{n} + 1^{+} B_{n})] + \\ \sum_{n} [\frac{P_{n}^{2}}{2} M + \frac{1}{2} w {(u_{n} - u_{n} - 1)}^{2}] + \sum_{n} χ (u_{n} + 1 - u_{n} - 1) B_{n}^{+} B_{n} \end{array}

Soliton solution in the Davydov model, describing the propagation of bioenergy in the form of a stable pulse, in the Nonlinear Schrödinger Equation:

ϕ (x, t) = \frac{\sqrt{μ_{D}}}{2} \sec h [\frac{μ_{D}}{r_{o}} (x - x_{o} - ν t)] \exp {\frac{h ν}{2 j r_{0}^{2}} (x - x_{o}) - \frac{E_{D}^{t}}{h}}

Pang's model improves this approach by introducing quasi-coherent quantum states and additional exciton-phonon interactions, increasing the thermal stability and lifetime of solitons at physiological temperatures (300 K). This perspective highlights the role of phonons as deformations of the protein lattice and solitons as stable carriers of energy and information, integrating biophysical properties essential for understanding energy transport in biological systems. Pang improved Davydov's model to solve thermal stability problems and introduced an approach based on quasi-coherent quantum states. Modified Pang’s Hamiltonian, incorporating additional interactions between excitons and protein chain deformations:

\begin{array}{l} H = \sum_{n} [\in_{0} B_{n}^{+} B_{n} - J (B_{n}^{+} B_{n} + 1 + B_{n + 1}^{+} B_{n})] + \sum_{n} (\frac{p_{n}^{2}}{2 M} + \frac{1}{2} w {(u_{n} - u_{n} - 1)}^{2}) + \\ \sum_{n} [x_{1} (u_{n + 1} - u_{n - 1}) B_{n}^{+} + B_{n} + x_{2} (u_{n + 1} - u_{n}) (B_{n + 1}^{+} B_{n} + B_{n}^{+} B_{n + 1})] \end{array}

Soliton solution in the Pang’s model, showing greater thermal stability and efficiency in bioenergy transport:

ϕ (x, t) = {(\frac{μ_{p}}{2})}^{1 / 2} \sec h [(μ_{p} / r_{o}) (x - x_{o} - ν t)] X \exp {i [ℏ ν / 2 J r_{0}^{2} (x - x_{0}) - E_{ν} t / ℏ]}

In BTTM, phonons can mediate mechanical interactions, linking structural components such as the cellular cytoskeleton, extracellular matrix, and collagen fibers. These coherent vibrations can facilitate intercellular communication, transmitting mechanical and energetic signals along connective tissue networks and aligning the cellular structure in a way that creates a global response to local stimuli. Thus, mechanical information (from pressure, stretching, or other external forces) is efficiently transmitted through the tensegrity network, impacting structure and function on a scale ranging from tissue to cell, and from cell to nucleus. Solitons can describe the transport of energy and information through biological structures in a stable and coherent manner, especially in a tensegrity network, along connective fibers such as collagen, microtubules, and DNA, which have flexoelectric and piezoelectric conformational properties.

Especially regarding human DNA, DNA synthesis in human fibroblasts was enhanced when exposed to sinusoidally variable magnetic fields for a wide range of frequencies.^55,56 In addition to its traditional role as a carrier of genetic information, it was demonstrated in a 3D model that DNA presents unique characteristics that position it as an electromagnetic bioresonator, a kind of fractal antenna that interacts with environmental electromagnetic fields. This property allows DNA to respond to specific frequencies, acting as a focal point for the reception and transmission of electromagnetic information within the human organism through solitonic frequencies. In its role as a resonator, DNA not only stores information, but also has the ability to modulate cellular signaling through interaction with electromagnetic fields, which reinforces its function as a biological “antenna”.⁵⁷

This suggests that DNA not only participates in biological processes in a passive manner, but also engages in an active dynamics of resonance and information transmission, interacting directly with other components of the biofield. The equation used by Singh et al.,⁵⁷ to express the energy transfer through the DNA molecule by means of solitons in this study is derived from the relative displacement power between adjacent DNA molecules and corroborates the claims of Reshetnyak et al.,⁵⁸ that a process of vibrational energy transfer along the protein molecule is achieved by solitons. Thus, the displacement current is given by:

I_{r d} = I_{d} (n + 1) - I_{d} (n)

where $I_{r d}$ is the relative displacement current – represents the variation in displacement current between two successive positions or states; $I_{d}$ is the displacement current in the state n and $I_{d (n + 1)}$ is the displacement current in the state $n + 1$ .

Then, the total power of interaction or displacement between two adjacent molecules in dynamic states can be represented as:

P_{r d} = J {(I_{r d} + I_{0})}^{2} - P_{0}

where $P_{r d}$ is the total power of interaction or displacement – represents the energy associated with the displacement of the current, considering the module of the currents; I₀ is the initial current or reference current, used as a point of comparison and; is the initial power or reference power, indicating the base value before displacement.

Added to the phenomena of mechanical resonance and interactions by phonons and solitons, the concept of vector potential, evidenced by the Aharonov-Bohm effect, offers a new dimension for informational communication in the biofield. This potential, even in the absence of a rotational magnetic field, is capable of altering the phase of particle wave functions, which influences tunneling processes and modulation of essential biochemical reactions. The phase change induced by the vector potential has direct implications on the interaction and transfer of electrical charges, such as electrons and protons, in redox reactions and biochemical processes in the organism.⁵⁹ This phase change is described by the equation:

Δ φ = (\frac{e}{ℏ}) \int A . d r

Where $Δ φ$ represents the phase variation; e is the charge of the particle $ℏ$ is the reduced Planck constant and; A is the vector potential and the integral is calculated along the path of the particle.

The rate of charge transfer in nonequilibrium systems, such as chemical reactions or bioenergetic processes, can be modulated by the phase difference (ɸ) induced by vector potentials. This relationship is expressed by the equation below, where V₀ represents the maximum transfer speed and ɸ reflects the direct contribution of the external vector potential. According to the authors, this equation suggests that vector potentials, even in weak or undetectable fields, can act as informational modulators, dynamically adjusting the speed of energy transport in living systems.

ν = ν {}_{0}s i n Φ

This mechanism, analogous to the Josephson Effect in quantum systems, suggests that the BTTM could operate as a coherent communication network, where information is transmitted in a non-linear manner and without the need for material conduits. This model adds a quantum basis to understand how the biofield acts as an informational network in the organism, with subtle electromagnetic signals and vector potentials modulating cellular functions and organizing biological processes in an integrated and coherent manner.

In a recent study, researchers explored in human osteosarcoma and mouse fibroblasts how biomolecular condensates, formed by membrane less phase separation, can generate forces that influence DNA organization and chromatin viscoelasticity. The researchers used light to induce condensate formation within the nucleus, with a wavelength of 395 nm, within the ultraviolet (UV) range, and stimulated specific regions within the cells. These condensates, which are composed of proteins and other molecules, form compartments that help organize DNA and regulate chromatin accessibility, facilitating specific biological processes, such as transcription and DNA repair.⁶⁰ In the context of the human biofield, this research offers complementary insights into how unconventional or biophysical forces such as light under these condensates can assist in the reorganization of biological structures without directly consuming energy from adenosine triphosphate (ATP), which for decades was considered the sole source of cellular energy. It also reinforces the effect of light even on viscoelastic materials and forces us to speculate on possibilities such as: Do nonlinear interactions and interfacial forces, similar to phonons and solitons, as in this proposal, play a significant role in maintaining and reorganizing the structural and functional integrity of living systems? Could the Raman effect, which occurs when light interacts with molecular vibrations or phonons in an inelastic scattering that alters the frequency of the reflected light,^61–63 disperse energy in materials at the DNA core? We propose that these forces could influence not only the physical organization but also the transmission of information through structures such as DNA, reinforcing the role of the biofield as a biophysical organizer through vibrations and resonances throughout the organism.

Quantum theory also offers insights into the properties of resonant components. A recent study in quantum electrodynamics highlighted how light particles, such as photons, can exhibit coherence in specific environments, influenced by phenomena such as the Casimir effect.⁶⁴ Associated with high-frequency electromagnetic signals in confined spaces, the Casimir effect may offer insights into how biophotons interact within the molecular and atomic structures of living organisms. Hypothetically, these biophotons could function as information mediators, bridging photonic and electronic communication. Based on wave-particle duality, it is suggested that biophotons could be transmitted by solitonic waves, ensuring efficient transport of energy and information without dissipation. However, their transient nature and potential for interaction with external electromagnetic fields pose significant challenges for experimental observation. For example, biophotons can disappear into subspaces or undergo changes in their electromagnetic signatures, making them difficult to measure directly, due to Raman scattering. These interactions highlight the potential vulnerability of biophoton-mediated processes to external electromagnetic waves, which can influence biological coherence and signaling mechanisms.

Other potential bioresonants are crystals located in the human brain, such as biogenic magnetite and pineal gland microcrystals. Biogenic magnetite (Fe₂⁺Fe₃⁺₂O₄) in the human brain, located in structures such as the hippocampus, frontal lobe and basal ganglia. Based on iron oxide, it forms crystals with sizes ranging from 10 to 50 nanometers, which allows high sensitivity to low-intensity electromagnetic fields.^65,66 Calcite microcrystals found in the pineal gland, located in the center of the brain, between the two hemispheres, in a small region called the epithalamus, situated behind and slightly above the pituitary gland and, due to its central position, is one of the most protected structures in the brain. Studies have shown that these crystals contain about 60% calcium and 30% oxygen, with 5% to 7% aluminum, as well as small amounts of other elements.^67,68 This chemical composition, including aluminum, allows these crystals to act not only as semiconductors and piezoelectric generators, but also as transmitters of electromagnetic signals. It is assumed that magnetite and calcite crystals have the ability to convert mechanical stimuli into electrical potentials and vice versa, making them essential to the human biofield, where they can detect and respond to specific frequencies, including environmental electromagnetic fields or electrosmog.

Tensegrity and biofield

R.Buckminster Fuller’s⁶⁹ idea that a tensile matrix is a structural system that combines stress and tension elements to form a stable network highlights “tensile integrity”, where stress elements are kept separate by continuous tension cables. Influenced by this, K. J. Pienta and D. S. Coffey¹⁴ extended Fuller’s conceptual application to the transfer of harmonic cellular information within a system termed the Tissue Tensegrity-Matrix System, composed of nuclear matrix, cytoskeleton, membrane matrix and components matrix. The authors argued that this system allows harmonic transfer of information and can be quantitatively analyzed using Fourier analysis.

Fourier Transformation:

F (k) = \int_{- \infty}^{\infty f (x) e^{{- 2 π i k x}}, d x}

Where F(k) is the Fourier transform of f(x), which components the amplitude and phase of the different frequencies of the components of f(x) in the frequency domain k; f(x) is the original function in the spatial or temporal domain, from its frequency components; k components the frequency variable (wavenumber) associated with the frequency component of f(x) (in the component with 2π in the exponential); e^-2^πikx is the complex exponential term that components a wave with frequency k in the transformed domain; is the integral over all values of x from -∞ to +∞, summing all contributions of f(x) weighted by e^-2^πikx to obtain F(k) ; dx is the differential of x, indicating that the integration is done with respect to the spatial variable.

Inverse Fourier Transform:

$F (x) = \int_{- \infty}^{\infty F (k) e^{- 2 π i k x} d k}$ ,

where f(x) is the original function in the spatial or temporal domain, from its frequency components; F(k) is the Fourier transform of f(x), which represents the amplitude and phase of the different frequencies of the components of f(x) in the frequency domain k; k components the frequency variable (wave number) associated with the frequency component of f(x); e^-2^πikx is the complex exponential term that components a wave of frequency k from its frequency components; $\int_{- \infty}^{\infty}$ is the integral over all values of k of -∞ a +∞, adding all the frequency components to reconstruct f(x); dk is the differential of k, indicating that the integration is done with respect to the frequency variable k.

A contemporary view of this concept was significantly expanded by Donald Ingber, who introduced the cellular tensegrity model, explaining how interactions between the cytoskeleton, extracellular matrix and nuclear architecture are coordinated through physical principles of stability and transmission of mechanical forces.⁷⁰ Tensegrity architecture was proposed as the fundamental principle of cellular mechanotransduction, allowing external mechanical forces to be converted into intracellular biochemical responses.⁷¹ Subsequent studies have consolidated the thesis that cellular tensegrity not only influences cellular morphology, but also modulates gene and protein signaling networks, impacting cellular behavior and pathophysiological processes.^72,73 These findings reinforce the hypothesis that the harmonic distribution of mechanical forces in the cellular matrix may be closely related to bioelectromagnetism and solitonic communication, suggesting that mechanical and electromagnetic aspects may be parts of the same continuum of biological information.

Applying the concept of tensegrity to the biofield suggests a network of mechanical and informational tension that permeates the entire component, connecting cells, molecules, and tissues without the need for direct physical connections. Instead, it is proposed that these tensions are transmitted by bioelectromagnetic fields and vectorial components, which act as mediators of a coherent and non-local vibrational communication. In BTTM, these vibrational modes disseminate signals throughout the component efficiently, without the need for a linear flow of energy or matter (Figure 2).

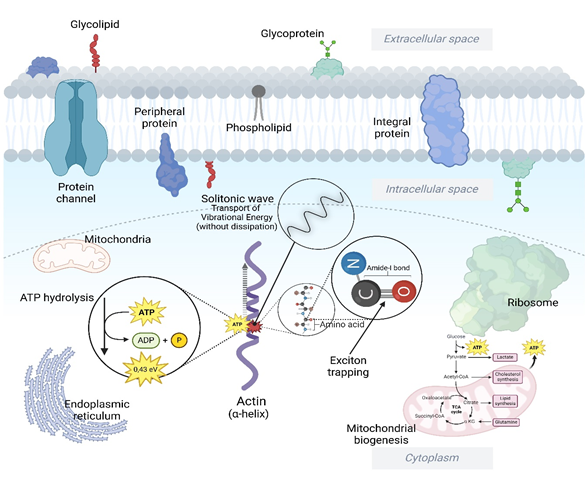
Figure 2 During interactions with structures such as alpha-helix protein filaments (which form part of F-actin or Beta-actin), hydrolysis can release vibrational energy. This energy does not dissipate immediately as heat, but according to Davydov's model, it can be channeled in the form of trapped excitons that create a coherent energy wave—the soliton. Energy transport by solitons could explain how the cell uses ATP energy efficiently for specific functions, without relying exclusively on conventional diffusive pathways.

Discussion

Although there are theoretical models of the biological properties of electrical components of living systems, there is still no conclusive experimental evidence to support the intrinsic bioelectromagnetism of DNA. Although oxygen bonds in DNA could theoretically generate electromagnetic radiation, these effects appear too weak to be detected by conventional means.⁷⁴ However, it has been shown that DNA can respond to specific human interests and positive emotions by changing its conformational state between more coiled and more exposed forms. These findings support the hypothesis that the heart, as a spontaneous generator of electromagnetic energy, can act in an integrated manner as an “information carrier” by transmitting vibrations or frequencies to DNA and thus modifying its conformational structure.⁷⁵

The hypothesis that this informational energy propagates through solitonic waves driven by bioelectric circuits, integrated into a tensegrity network orchestrated by the biofield, is innovative and provocative. However, the soliton model proposed by Pang was initially criticized, based on the claim that consistent propagation of excitations, with phase preservation, would be unfeasible for vibrations in α-helical peptide groups due to the predominance of thermal fluctuations and disorder effects at room temperature.⁷⁶ This criticism was later challenged by studies that showed significant changes in the bioenergy transport characteristics in Pang's model, under different external electric and electromagnetic fields. Infrared absorption spectra in collagen with α-helical structure confirm these changes, bringing new perspectives to the model.⁵⁴

Several models in physics offer plausible explanations for endogenous energy transfer in nonequilibrium thermodynamic systems that maintain a high degree of organization.^77–80 Based on this premise, speculation arises about the crucial role of biophotons in the endogenous-exogenous transfer of energy in living organisms, biophotons are emitted in a range that goes from UV to near infrared (IR), covering a wide range of frequencies in the electromagnetic spectrum.⁸¹ The emission of biophotons is closely associated with the dissipation of energy in biological systems, suggesting that they play a vital role in the energetic communication between the organism and the external environment. This endogenous electromagnetic field generated by biophotons could, theoretically, facilitate the propagation of solitons beyond the limits of the body, creating a coherent “channel” for the transmission of energy.

Biophotons, which are emitted in the visible to near-infrared range, have enough energy to interact with the characteristic vibrational states of proteins. On the other hand, solitons are associated with low-energy vibrations, such as those observed in the mid-infrared, including the 1650 cm⁻¹ peak related to the amide I band of proteins with single chains (or a single helix), which are more likely to maintain soliton stability and therefore resonate better with biophotons. If we consider that energy transport in solitons involves specific vibrational states or excitations of proteins, low-energy biophotons (especially in the near-infrared limit) could interact with these states. This resonance could facilitate energy transport or modulate soliton stability.

In particular, when DNA is excited by biophotons, excitons—collective excitations of electrons and holes—can be generated. These excitons, in turn, can be transported along the DNA helix by solitons.^53–57^,82 The vibrations or rotations induced by biophotons have the potential to excite these solitons, which propagate along the DNA chain, carrying with them the energy associated with the excitons. Excitons are composed of electrons and holes, and when these electrons move, they generate electromagnetic waves. This process involves a transfer of quantum energy along biological molecules. By extending this mechanism to the organism as a whole, we can conceive of the human body as a biological “electrical superconductor”, in which coordinated quantum processes allow the generation of electromagnetic radiation. However, due to the dissipative nature of the biological medium and the properties of the external environment, this radiation would be limited to short distances, significantly restricting its propagation beyond the limits of the body.

Complementary to the biophoton energy transfer pathway, torsion fields offer an innovative paradigm for understanding how subtle energies can be transferred between living systems.^83–85 These fields, described as variations in the orientation of space-time induced by electromagnetic currents and charges, can act as non-local mediators of cellular communication. Within the BTTM model, torsion fields can be integrated as agents that enhance the bidirectional vibrational coherence between phonons and solitons in the tissue tensegrity matrix, connecting donor/therapist and recipient/patient. This interaction suggests a mechanism in which electromagnetic and mechanical information, carried by stable solitons, modulate cellular processes from subatomic levels. Furthermore, due to the universal physical properties of torsion fields, such interactions could justify therapeutic effects over long distances. Thus, torsion fields may play an essential role in the homeodynamic regulation and self-repair of biological systems. During the emission of external Qi, an extraordinarily high biomagnetic field strength was captured, measured at 10⁻³ gauss (mGauss), a value significantly higher than that observed under normal human conditions.⁸⁶ Furthermore, low-frequency oscillations (0–40 Hz) were measured during Biofield Therapy sessions, with significant increases in field activity during and after sessions compared to previous periods. These characteristics were associated with improvements in patient-reported well-being.⁸⁷

In recent experiments, Biofield Therapy has demonstrated significant effects in in vitro models, altering the tumor microenvironment and reducing “stemness” (stem cell characteristics) in cancer cells, suggesting a potential impact on tumor aggressiveness.⁸⁸ They have also shown promising effects in RCTs (randomized controlled clinical trials) in alleviating symptoms associated with mental disorders in patients, such as those undergoing cancer treatment, as well as mitigating fatigue and chronic pain in various health conditions.^89–96

In patients with knee osteoarthritis, treated with external Qigong, non-significant reductions in pain and functional limitations were shown compared to the control group. However, the variability of results between therapists, even under personalized experimental protocols, was suggested by the authors as an avenue to be explored in future investigations.⁹⁷ This raises questions about the role of intention, therapist technical skill, and individual biological factors related to the BTTM. Several individual therapist/source factors can influence the success of biofield therapies. Intentionality, for example, appears to act as a “turbine” in the biofield, generating larger mechanical vibrations (phonons), directing nonlinear waves (solitons) in biological materials, and propagating torsion waves exogenously, amplifying therapeutic effects in promoting homeostasis and recovery.

Conclusion

The classification of bioelectromagnetic components into self-organized, dynamic, and non-equilibrium systems is fundamental to conceptualizing the biofield as a biological continuum with integrated electromagnetic properties. In this context, it is equally essential to propose a theoretical system capable of integrating such components and providing a robust conceptual basis for this circuitry. The BTTM model presents an innovative approach to systemic organization and communication in living organisms. By incorporating bioelectromagnetic and mechanical elements, the BTTM operates as an informational tensegrity network in which cells, molecules, and DNA interact coherently with internal and external electromagnetic fields, supported by a continuous feedback system. This matrix facilitates the organized transmission of vibrational signals, such as phonons and solitons, particularly in peptide structures, modulating cellular responses and promoting resonance between different levels of biological structures.

Evidence suggests that the BTTM not only ensures the structural and mechanical integrity of tissues, but also plays a central role in mediating biophysical information, which has significant implications for understanding the mechanisms of self-regulation and self-healing in living systems. Furthermore, the vectorial potential and biophysical resonances discussed in the scope of the biofield offer promising scientific foundations for the development of therapeutic interventions based on energetic approaches, such as bioenergetic medicine and field therapies. Future experimental studies using bioquantum technology will be crucial to validate the clinical and therapeutic applicability of the BTTM model, especially with regard to the interactions between subtle electromagnetic fields and biological tissues. These advances may open new horizons in biomedical science and integrative medicine.

Author contributions

R.S. researched and wrote the manuscript.

Acknowledgments

I would like to express my deepest gratitude to Dr. Stuart Newman, whose insightful feedback and guidance were instrumental in refining the theoretical framework of tensegrity in this work. Finally, I extend my appreciation to all researchers and clinicians who explore the intersection of biophysics and medicine, pushing the boundaries of scientific inquiry toward more integrative and holistic health paradigms.