As the consumption of goods, services, and granting of credit increase, it becomes necessary to control the risk of the process. This measure aims to avoid possible defaults greater than what financial institutions can support while allowing for profit generation. Various statistical techniques can be used to build models that present the risk panorama, one of which is survival analysis. The application of this technique in the financial market seeks to study, for example, the time it takes for an individual to recover credit after the end of a financial crisis in their country. The use of such data can support the prediction of the ideal amount of credit to be provisioned in possible crisis scenarios and infer when the resumption of credit operations may occur. In this context, this work aims to study two defective regression models for modeling zero-adjusted survival data in the credit risk scenario. This approach accommodates three types of units: customers with "zero" survival times, that is, early failures, customers susceptible, and not susceptible to the event of interest. The methodology studied will be applied to a database provided by a leading institution in credit services and information in Brazil.

Keywords: survival analysis, financial data, credit risk, cure fraction, defective distribution, zero-adjusted

Risk can be defined as the volatility of unexpected events, such as the representation of the value of assets, equity or profit.¹ In this context, in financial institutions, a credit granting operation is characterized as credit risk. This type of risk is inherent to any financial transaction, being defined as the possibility of non-compliance with contractual obligations by the debtor, who does not honor the agreement established with the creditor at the time of contracting. Therefore, it is extremely important that financial institutions adopt appropriate measures and procedures to manage credit risk, ensuring the financial health of the institution and the confidence of the market and clients.

Credit analysis plays a crucial role in companies, as it is essential to assess the individual’s financial capacity and relationship with the market to determine the viability of granting credit. The analysis takes into account income, credit history, among other factors, in order to avoid financial losses for the institution. In this sense, the use of credit score models proves to be beneficial for allowing consistency in decisions in credit analysis, creating automation in granting, increasing the value of the analysis, ability to monitor and manage the risk of portfolio credit, among others. Furthermore, according to Silva, when considering the dynamics to which economic scenarios are linked and the way in which this directly affects the risk of default, the decision to grant credit, based on risk models, must be monitored and revised when necessary.

The occurrence of a financial crisis in the country is characterized by a reduction in the level of production in the country, resulting in a series of impacts. Among these impacts, it is possible to highlight the population’s indebtedness, caused by several factors, such as increased inflation, high unemployment and restricted access to credit. In the current scenario, the recovery of the financial system could be a slow and uncertain process, lacking assertive predictions about the ideal moment for recovery. Therefore, it is essential to use statistical models, such as Survival Analysis, which is a tool that can provide important support in these circumstances.

Survival analysis is made up of a set of statistical techniques and methods used to study the time elapsed until the occurrence of an event of interest. The term survival analysis is commonly used in the medical field, where the time until failure can be characterized as: death, cure, onset of a disease, side effect of a medication, among others. However, in addition to the medical area, survival analysis can be applied in other areas, such as the financial market.

Cure fraction modeling, also known as long-term modeling, studies cases in which, presumably, there are observations that are not susceptible to the event of interest. Boag² was one of the pioneers of long-term modeling. Subsequently, other models were proposed, such as the standard mixture model by Berkson & Gage,³ the unified cure fraction model by Rodrigues,⁴ among others. In this type of modeling, there are individuals who are not susceptible to the occurrence of the event of interest, and can be considered as cured individuals/immune to the event of interest and the survival data set to which they belong has a cure fraction. In the financial market, the objective is to predict the recovery time of customers, with the recovered customer being the customer who returns to payment status. The use of long-term models in the financial market is considered a good tool for studying the time until the event of interest occurs, such as the return period until the payment status or the realization/delay of a portion of loan Toledo.⁵

Thus, applied in the financial market, long-term survival analysis is used to estimate the time of an event, such as the time elapsed from the acquisition of a loan until the delay in one of the installments, or even, as studied by Granzotto et al,⁶ the beginning of the customer’s relationship with the institution until the breakdown of that relationship.

However, in some studies there are individuals susceptible to early failures, which result in survival time equal to or close to zero. In this case, this scenario will be referred to as zero-adjusted. Therefore, in the context of cure fraction, defective models offer the strategy to model zero-adjusted survival data. Although some articles have already used the idea of defective models, Balka,⁷ Rocha et al.,⁸ Scudilio et al.⁹ and Calsavara et al.¹⁰ have recently popularized the term "defective". In the literature, there are several probability distributions that have a defective form.

In this context,the main objective of this paper is to consider an approach proposed by Calsavara et al.,¹⁰ called “Zero-Adjusted regression models” for analyzing credit risk data in the financial market. This approach makes it possible to accommodate three types of units, such as customers with “zero” survival times, i.e., early failures, customers susceptible and not susceptible to the event of interest. To estimate the survival function with the possibility of cure fraction and a lifetime proportion set to zero, we consider the defective Gompertz and Inverse Gaussian models. The dataset used in the application was analyzed by Toledo et al.⁵ The data were provided by a Brazilian financial institution, which provides services aimed at the credit market, containing information involving characteristics related to the habits and customs of individuals regarding commitments involving credit requests.

The rest of the article is organized as follows. In Section 2, we present the background on cure rate model and defective model. In Section 3, we present the formulation the zero-adjusted defective model and Inference methods based on the likelihood function. In Section 4, we apply the proposed model to the real data set used in the application was analyzed by Toledo et al.⁵ The data were provided by a Brazilian financial institutions. Finally, some concluding remarks are considered in Section 5.

In this section, we present a brief description of the cure rate model proposed by Tsodikov and Yakovlev et al.,¹ Ibrahim et al.,¹¹ later extended by Rodrigues et al.⁴ as well as description of defective model.⁷

Cure rate models

The survival theory has been widely explored by many researchers in various areas, with a major focus on analysis of clinical data. Generally the survival function$S\left(t\right)=P(T>t)$ is the function used to represent the random behavior of T. A property of $S\left(t\right)$ is that it goes to zero as the time pass, which characterizes an event of interest that eventually always occur.

However, there are situations in which a portion of the population is considered cured and cannot fail. For example, there are cases when it is considered the recurrence of a cancer. Some people can have the recurrence, however, there may be some others that is completely cured from that cancer and, therefore, it would never recur. To solve such problems, Berkson & Gage,³ based on the work of Boag,² proposed the standard mixture model for cured fraction. The survival function is set to

$S_{pop}\left(t\right)=p+\left(1-p\right)S_0\left(t\right),$   (1)

 in a way that $S_0\left(t\right)$ is a proper survival function. Thus, it follows that $S\left(t\right)$ converges top as the time increases. The above function has the following properties:

• If $p=0$ , then $S_{pop}\left(t\right)=S_0\left(t\right)$ ;
• $S_{pop}\left(t\right)=1$ ;
• $S_{pop}\left(t\right)$ is decreasing;
• ${\text{lim}}_{t\to \infty }{S}_{pop}\left(t\right)=p$

The last property demonstrates that the population survival function is improper, as the survival curve stabilizes at p, which exactly represents the cure probability of the population.

In addition to this approach, we have a unified long-term theory, proposed by Rodrigues et al.⁴ that generalizes, among others, the mixture model. Let N be a random variable that represents the number of causes of risk, for a particular event of interest, with probability distribution of $p_N=P\left(N=n\right)$  in which $n=0,1,2,\dots$ . In this case,N is a latent random variable. Given $N=n$ , let $Z_v,v=1,\dots ,n$ , be independent, non-negative random variables, with distribution $F\left(t\right)=1-S\left(t\right)$ . Consider also that N is independent of $Z_v$ , where $Z_v$  represents the time until the occurrence of an particular event of interest, because of the $v$ -th cause of risk.

The time of occurrence of the event of interest is defined as:

$T=min\left\{Z_1,Z_2,\dots ,Z_N\right\},$   (2)

in which $P\left[Z_0=\infty \right]=1$ , leads to a proportion $p_0$  of the non-susceptible subjects to the event of interest. The variables $Z_v$  are latent and T is an observable random variable or censoring. The survival function of the random variable T is given by:$S_{pop}\left(t\right)=P[T>t]$ .

Let $\left\{a_n\right\}$  be a sequence of real numbers and $s\in \left[0,1\right]$ . Consider then the following:

$A\left(s\right)=a_0+a_{1}s+a_2{s}^2+\dots .$

According to Feller,¹² if $A\left(s\right)$ converges, then $A\left(s\right)$ and defined as the generating function of the sequence fang. Given a proper survival function $S\left(t\right)$ , the survival function of the random variable, as in (2), is given

$S_{pop}\left(t\right)=A\left[S\left(t\right)\right]={\displaystyle \sum }_{n=0}^{\infty }{p}_n{[S\left(t\right)]}^n$   (3)

This implies that ${\text{lim}}_{t\to \infty }{S}_{pop}\left(t\right)=P\left[N=0\right]=p_0$ , with $p_0$  denoting the cured fraction.

The survival function $S_{pop}\left(t\right)$  obtained in (3) is not proper. The associated density and hazard function are given, respectively, by:

$f_{pop}\left(t\right)=f\left(t\right)\frac{d}{ds}\left[A\left(s\right)\right]s_{s=S\left(t\right)},$   (4)

$h_{pop}\left(t\right)=\frac{f_{pop}\left(t\right)}{S_{pop}\left(t\right)}=f\left(t\right)\frac{\left[A\left(s\right)\right]s_{s=S\left(t\right)}}{S_{pop}\left(t\right)}.$   (5)

Some examples of generating function can be obtained by using the distributions: Bernoulli, binomial, negative binomial, Poisson, geometric, power series, among others. If we assume the distribution foris Bernoulli, then $S_{pop}\left(t\right)$  is the same proposed in Berkson & Gage.³

Defective model

A distribution is considered defective if the integral of its density function does not result in 1, but in a value $p\in \left(0,1\right)$ when the domain of the parameters is changed. In defective models, it is possible to estimate a cure rate using a naturally improper distribution. Instead of directly estimating the proportionas a mixture model, we employ a distribution by altering the domain of its parameters.

In a defective distribution, the cumulative function no longer approaches to 1, but to p and, therefore, the survival function approaches to $1-p$ . Figure 1 illustrates the cumulative function of a defective distribution. Obviously, the defective distribution is not proper.

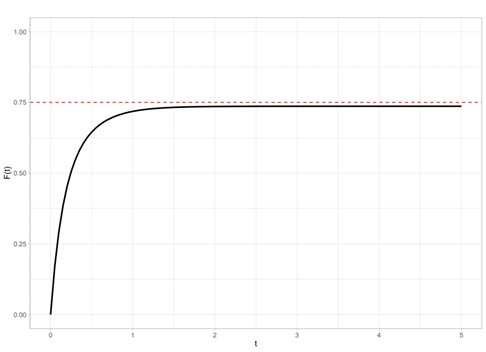
Figure 1 Defective accumulated distribution function.

In the literature, there are two known distributions that can be used for this purpose: the inverse Gaussian and Gompertz distributio.⁸

The defective gompertz distribution: The Gompertz distribution is often used to model survival data in various areas of knowledge Gieser et al.¹³ The probability density function for the Gompertz distribution is given by

$f\left(t\right)=b{e}^{at}{e}^{-\frac{b}{a}\left(e^{at-1}\right)}.$   (6)

where $a>0,b>0$ and $t>0$ . The corresponding survival function and hazard function are given respectively by

$S\left(t\right)=e^{-\frac{b}{a}\left(e^{at-1}\right)},$   (7)

$h\left(t\right)=b{e}^{at}.$   (8)

The defective Gompertz distribution is the Gompertz distribution that allows the scale parameter to have negative values ($a<0$ ). The cure fraction P in the population is calculated when the limit of the survival function (7) tends to infinity with ($a<0$ ), that is,

$p=\underset{x\to \infty }{\text{lim}}S\left(t\right)=\underset{x\to \infty }{\text{lim}}{e}^{-\frac{b}{a}\left(e^{at-1}\right)}=e^{b/a}\in \left(0,1\right)$   (9)

The defective inverse gaussian distribution: The inverse Gaussian distribution arises as the first passage time of a Wiener process.⁷ Lee and Whitmore¹⁴ noted its potential as models for cure rate. Its density function is

$f\left(t\right)=\frac{1}{\sqrt{2b\pi t^3}}\text{exp}\left\{-\frac{1}{2bt}{(1-at)}^2\right\},$   (10)

 where $a>0,b>0$ and $t>0$ . The corresponding survival function is given by,

$S\left(t\right)=1-\left[\text{Φ}\left(\frac{-1+at}{\sqrt{bt}}\right)+e^{2a/b}\text{Φ}\left(\frac{-1-at}{\sqrt{bt}}\right)\right],$   (11)

 where $\text{Φ}(\cdot )$ denotes the cumulative distribution of the standard normal. The hazard function is

$h\left(t\right)=\frac{\frac{1}{\sqrt{2b\pi t^3}}\text{exp}\left\{-\frac{1}{2bt}{(1-at)}^2\right\}}{1-\left\{\text{Φ}\left(\frac{-1+at}{\sqrt{bt}}\right)+e^{2a/b}\text{Φ}\left(\frac{-1-at}{\sqrt{bt}}\right)\right\}}.$   (12)

The defective inverse Gaussian distribution is the inverse Gaussian distribution that allows negative values of a. The cure fraction P in the population is calculated when the limit of the survival function (11) tends to infinity with $\left(a<0\right)$ that is,

$p=\underset{t\to \infty }{\text{lim}}S\left(t\right)=\underset{t\to \infty }{\text{lim}}1-\left[\text{Φ}\left(\frac{-1+at}{\sqrt{bt}}\right)+e^{2a/b}\text{Φ}\left(\frac{-1-at}{\sqrt{bt}}\right)\right]=1-\text{exp}\left\{\frac{2a}{b}\right\}\in \left(0,1\right).$   (13)

In the context of cure fraction, defectives models offer the strategy to model zero-adjusted survival data. In this sense, instead of estimating the cure fraction directly, as in the standard mixture model, the defective model is an alternative for modeling long-term service life data. To accommodate zero-adjusted lifetimes in defectivos models, Calsavara et al.,¹⁰ proposed a new survival function as follows:

$S_{pop}\left(t;{\theta }^{*}\right)=\left(1-p_0\right)S\left(t;\theta \right), t>0,$   (14)

where $S\left(\cdot ;\theta \right)$ is a proper or improper survival function,$0\le p_0\le 1$ denotes the zero-adjusted proportion and ${\theta }^{*}={\left(p_0,{\theta }^{\top }\right)}^{\top }$  is a vector of parameters.

It is important to highlight that if $S\left(\cdot ;\theta \right)$ is a proper survival function, that is, ${\text{lim}}_{t\to \infty }S\left(\cdot ;\theta \right)=0$ , the model (14) becomes a standard zero-adjusted survival model. Otherwise, if the survival function $S\left(\cdot ;\theta \right)$ is improper, then the proposed model satisfies,

$S_{pop}\left(t;{\theta }^{*}\right)=\left(1-p_0\right)\le 1,$

and the limit of the survival function is

$p_1=\underset{t\to \infty }{\text{lim}}{S}_p\left(t;{\theta }^{\text{*}}\right)=\left(1-p_0\right)\underset{t\to \infty }{\text{lim}}S\left(t;\theta \right)=\left(1-p_0\right)p\in \left(0,1\right),$

where P is the cure fraction of the improper/defective distribution. Models that consider such proportions simultaneously are called zero-inflated (or zero-adjusted) cure rate survival models, or zero-inflated cure rate models. Figure 2, we illustrate the behavior of the survival function for this model.

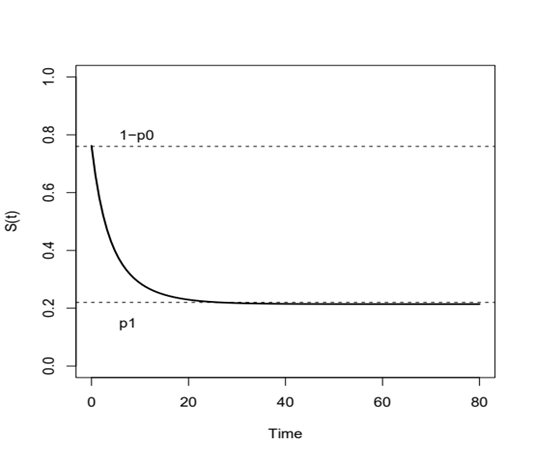
Figure 2 Survival function of the zero-inflated cure rate model.

 The associated cumulative distribution and probability density functions are, respectively,

$F_{pop}\left(t;{\theta }^{*}\right)=p_0+\left(1-p_0\right)F\left(t;\theta \right), t>0,$

 and

$f_{pop}\left(t;{\theta }^{*}\right)=\{\begin{array}{l}{p}_0, \text{if} t=0,\hfill \\ \left(1-p_0\right)f\left(t;\theta \right), \text{if} t>0.\hfill \end{array}$

Note that if $p_0=0$ , the faulty standard model is obtained as a special case.

Defective model gompertz zero-adjusted

Based on the equation (14) with the survival function in (7), the survival function of the zero-adjusted Gompertz defective model will be given by:  

$S_{pop}\left(t;{\theta }^{*}\right)=\left(1-p_0\right)\text{exp}\left\{-\frac{b}{a}\left(e^{at}-1\right)\right\},$

where ${\theta }^{*}={(p_0,a,b)}^{\top }$  is a vector of parameters, where $0\le p_0\le 1$ ,$a\in \mathcal{R}$ and $b>0$ .

The corresponding probability density function is defined by,

$f_{pop}\left(t;{\theta }^{*}\right)=\left(1-p_0\right)b\text{exp}\left\{at-\frac{b}{a}\left(e^{at}-1\right)\right\}.$

As seen in the defective Gompertz distribution (6), the defective zero-adjusted Gompertz distribution also allows negative values for the parameter. In this case, the corresponding cure fraction whenis given by

$p_1=\underset{t\to \infty }{\text{lim}}{S}_p\left(t;{\theta }^{*}\right)=\left(1-p_0\right)\underset{t\to \infty }{\text{lim}}{e}^{\left(-b/a\right)\left(e^{at}-1\right)}=\left(1-p_0\right)e^{b/a}=\left(1-p_0\right)p\in \left(0,1\right).$   (15)

From (15) the defective zero-adjusted Gompertz distribution shows that the cure fraction decreases asincreases.

Defective model gaussian-inverse zero-adjusted

Again, based on the equation (14) with the survival function in (11), the survival function of the zero-adjusted Gaussian-Inverse defective model is given by:

$S_{pop}\left(t;{\theta }^{*}\right)=\left(1-p_0\right)\left[1-\left\{\text{Φ}\left(\frac{-1+at}{\sqrt{bt}}\right)+e^{2a/b}\text{Φ}\left(\frac{-1-at}{\sqrt{bt}}\right)\right\}\right],$

 where ${\theta }^{*}={(p_0,a,b)}^{\top }$  is a vector of parameters, where $0\le p_0\le 1$ ,$a\in \mathcal{R}$ and $b>0$ .

The corresponding probability density function,is given by,

$f_{pop}\left(t;{\theta }^{*}\right)=\frac{1-p_0}{\sqrt{2b\pi t^3}}\text{exp}\left\{-\frac{1}{2bt}{(1-at)}^2\right\}.$

Following the same concept as the zero adjusted Gompertz defective model, the zero adjusted Gaussian-Inverse defective model allows $a<0$ , and its cure fraction is,$p_1=\underset{t\to \infty }{\text{lim}}{S}_p\left(t;{\theta }^{*}\right)=\left(1-p_0\right)\underset{t\to \infty }{\text{lim}}\left[1-\left\{\text{Φ}\left(\frac{-1+at}{\sqrt{bt}}\right)+e^{2a/b}\text{Φ}\left(\frac{-1-at}{\sqrt{bt}}\right)\right\}\right]$ $=\left(1-p_0\right)\left(1-e^{2a/b}\right)=\left(1-p_0\right)p\in \left(0,1\right).$   (16)

From the (16) the zero-adjusted Inverse Gaussian distribution shows that the cure fraction decreases as  increases.

In this sense, if the estimated parameter is negative ($a<0$ ), then the cure fraction for the defective Gompertz and Inverse Gaussian models defined as zero can be obtained, respectively, from (15) and (16). Otherwise, if the estimated model parameter is positive, there will be no cure fraction, according to the zero-adjusted defective models.

The advantage of the model proposed by Calsavara et al.¹⁵ is the ability to accommodate a zero-adjusted life expectancy proportion, as well as the possibility of a fraction of cure in the population.

Inference

In this section, we describe the inference for the model parameters based on a maximum likelihood approach and also on the asymptotic theory of large samples. Let $T\ge 0$ be a random variable that represents the time until the event of interest occurs. Consider the time of the indicator variable ${\delta }_i^{\text{*}}$ , that is,${\delta }_i^{\text{*}}=0$ if $T=0$ (survival time set to zero) and ${\delta }_i^{\text{*}}=1$  if $T>0,=1,\mathrm{...},n.$ Furthermore, let ${\delta }_i$  be the censorship indicator variable, where ${\delta }_i=0$  if the data is censored and ${\delta }_i=1$  otherwise. The explanatory variables will be incorporated into the model with a set of two-variable vectors,$x_1\in {ℝ}^{s+1}$ and $x_2 in{ℝ}^{q+1}$ , such that $x^{\top }=\left(x_1{}^{\top },x_2{}^{\top }\right)\in {ℝ}^w$  is a covariate vector with dimension w, where $w=s+q+2$ .

According to Calsavara et al.¹⁵ the logito and log link functions were considered, being:

$\text{ln}\left(\frac{p_{0x_{1i}}}{1-p_{0x_{1i}}}\right)=x_{1i}{}^{\top }{\beta }_0 \text{e} \text{ln}b\left(x_{2i}\right)=x_{2i}{}^{\top }{\beta }_1,$

 where $x_{1i}^{\top }=\left(1,x_{1_{i1}},\mathrm{...},x_{1_{is}}\right)$  and $x_{2i}^{\top }=\left(1,x_{2_{iq}},\mathrm{...},x_{1_{is}}\right)$  are the sets of covariates and ${\beta }_0^{\top }=\left({\beta }_{00},{\beta }_{01},\mathrm{...},{\beta }_{0s}\right)$  and ${\beta }_1^{\top }=\left({\beta }_{10},{\beta }_{11},\mathrm{...},{\beta }_{1q}\right)$  and their regression coefficients, respectively. In this way, the link function will depend on the covariates and can be expressed as follows

$p_{0x_{1i}}=\frac{\text{exp}\left\{x_{1i}{}^{\top }{\beta }_0\right\}}{1+\text{exp}\left\{x_{1i}{}^{\top }{\beta }_0\right\}} \text{and} b\left(x_{2i}\right)=\text{exp}\left\{x_{2i}{}^{\top }{\beta }_1\right\}.$

In practice, the covariate vectors can be the same, that is,$x=x_1=x_2$ . Furthermore, the logit and log link functions will be used to maintain the range of values of $p_0$ and b, respectively. Other linkage functions can be used for the proportion of failures, such as the probit and complementary log-log linkage functions.

In this sense, in the data set to be observed, we have $D=\left(t,\delta ,{\delta }^{*},\mathbb{X}\right)$ , on what $t={(t_1,\mathrm{...},t_n)}^{\top }$ will be the observed lifetimes, $\delta ={({\delta }_1,\mathrm{...},{\delta }_n)}^{\top }$ and,${\delta }^{*}={({\delta }_1^{\text{*}},\mathrm{...},{\delta }_n^{\text{*}})}^{\top }$ are, respectively, the censoring and censoring time indicators, and $\mathbb{X}$ is the matrix containing the covariate information.

Considering that’s $T_i$ are dependent and identically distributed random variables with the survival function specified by $S_p\left(\cdot ;\vartheta \right)$ ,on what $\vartheta ={(a,{\beta }_0,{\beta }_1)}^{\top }$  é um vetor de parâmetros desconhecidos. The likelihood function ofunder non-informative censoring is expressed as,  

$L\left(\vartheta ;D\right)\propto {\displaystyle \prod }_{i=1}^n{(p_{0x_{1i}})}^{1-{\delta }_i^{\text{*}}}{\left\{f_p{(t_i;\vartheta ,x_{1i},x_{2i})}^{{\delta }_i}{S}_p{(t_i;\vartheta ,x_{1i},x_{2i})}^{1-{\delta }_i}\right\}}^{{\delta }_i^{\text{*}}}.$  (17)

The corresponding log-likelihood is given by

$l\left(\vartheta \right)=\text{log}L\left(\vartheta ;D\right)$

$\propto {\displaystyle \sum }_{i=1}^n\left(1-{\delta }^{\text{*}}\right)\text{log}\left(p_{0x_{1i}}\right)+{\displaystyle \sum }_{i=1}^n{\delta }_i^{\text{*}}{\delta }_i\text{log}{f}_p\left(t_i;\vartheta ,x_{1i},x_{2i}\right)+{\displaystyle \sum }_{i=1}^n\left(1-{\delta }_i\right){\delta }_i^{\text{*}}\text{log}{S}_p\left(t_i;\vartheta ,x_{1i},x_{2i}\right).$

The previous log-likelihood function can be rewritten as follows,  

$l\left(\vartheta \right)\propto {\displaystyle \sum }_{i=1}^n\left(1-{\delta }^{\text{*}}\right)\text{log}\left(p_{0x_{1i}}\right)+{\displaystyle \sum }_{i=1}^n{\delta }_i^{\text{*}}{\delta }_i\text{log}\left(1-p_{0x_{1i}}\right)$

$+{\displaystyle \sum }_{i=1}^n{\delta }_i^{\text{*}}{\delta }_i\text{log}f\left(t_i;\vartheta ,x_{1i},x_{2i}\right)+{\displaystyle \sum }_{i=1}^n\left(1-{\delta }_i\right){\delta }_i^{\text{*}}\text{log}S\left(t_i;\vartheta ,x_{1i},x_{2i}\right),$

on what $f\left(\cdot ;\vartheta ,x_{1i},x_{2i}\right)$ e $S\left(\cdot ;\vartheta ,x_{1i},x_{2i}\right)$ are, respectively, the probability density function and the survival function associated with the defective distribution. The full proof of the likelihood function can be found in Calsavara et al.¹⁵

Maximum likelihood estimates of the parameters are obtained by numerically maximizing the log-likelihood function. There are several methods for this numerical maximization, however, the optim routine in the statistical software R was used for this maximization.

Therefore, the asymptotic properties of maximum likelihood estimates are necessary to construct confidence intervals and test hypotheses about model parameters. Under certain conditions,has an asymptotic multivariate normal distribution with meanand variance $\Sigma \left(\widehat{\vartheta }\right)$ , being estimated by,  

$\widehat{\Sigma }\left(\widehat{\vartheta }\right)={\left\{-l\left(\vartheta \right)\vartheta d{\vartheta }^{\top }{}_{\vartheta =\widehat{\vartheta }}=\widehat{\vartheta }\right\}}^{-1}$

Thus, an approximate confidence interval of $100\left(1-\alpha \right)\text{\%}$  for ${\vartheta }_i$  is $\left({\widehat{\vartheta }}_i\pm z_{\alpha /2}\sqrt{{\text{Σ}}^{ii}}\right)$ , where ${\text{Σ}}^{ii}$  denotes the ith element of the diagonal of the inverse of $\Sigma$ evaluated at $\widehat{\vartheta }$ and $z_{\alpha }$ denotes the $100\left(1-\alpha \right)$  percentile of the standard normal random variable.

The results of the asymptotic normality of maximum likelihood estimates are valid under certain conditions. In Calsavara et al.¹⁵ a simulation study was carried out to verify whether the usual asymptotes of maximum likelihood estimates are valid, since simulations have been used in many works to verify the asymptotic behavior of maximum likelihood estimates, especially when a Analytical investigation is not trivial.

Data description

In this study, the dataset for this application was provided by a financial institution providing credit-oriented services. These data were analysed by Toledo et al.⁵ considering the model proposed by Ribeiro et al.¹⁶ The period considered was after the Brazilian economic recession, starting in mid-2014, in which there was an increase in the financial crisis in the country. For this application, a random sample of 9,645 CPFs will be considered. The main characteristic of the individuals that make up this data set is the acquisition of debts, that is, there are customers with overdue and unpaid debts in the period from July/2015 to December/2015.

The process of collecting outstanding debts is done in a traditional way. This type of process can be carried out through telephone charges, collection letters or extrajudicial calls. Devido ao cenário da crise econômica, há a lentidão do processo de restituição do status do clientes de inadimplente para adimplente, sendo necessário a utilização de modelos estatísticos para estimar o prazo para a ocorrência destes eventos. The failure time in this study is the time from the date of debt acquisition to the completion of the study, a period of 24 months. In this context, to identify differences in customer behaviors for different scenarios, the situation will be studied using two covariates.

• Consultation information: Indicates whether the customer in question has been consulted by companies (from any segment) on credit reports in the past 180 days.
• Type of debt: Indicates whether the debt acquired in the period of the economic crisis is from the financial segment (Banks) or other segments.

In Table 1 shows the covariates according to their categories.

Furthermore, through the data set it is possible to verify the distribution of clients subgroups, since it is possible to perceive different behaviours in relation to the payment status recovery time for different clients subgroups, being,

1. Client having an event at time zero: Indicates clients who have settled their debt at time zero, immediately recovering their ability to pay;
2. Client susceptible to the event: Indicates clients who settled their debt within the observed period of 24 months, that is, they reversed their debts over the period and as of such settlement recovered their ability to pay;
3. Client not susceptible to the event: Clients not susceptible to the event of interest, which according to the theory are considered immune/cured, that is, they are clients who continued with their outstanding debts after the 24-month period, thus remaining with the status of default.

In Table 2 there is the number of each subgroup present in the data set.

Therefore, Table 2 shows that there is a concentration of events at time zero, accounting for about 23.76% of the observations, identifying an excess of zeros. In addition, aroundof clients do not present the event of interest, which is theoretically considered immune. Finally, aboutof the clients had an interest event, that is, they paid off the debt within 24 months.

The Figure 3 shows the distribution of debt settlement times for the observed data set. In this sense, it is possible to notice in the Figure 3, the inflation of the zeros for this data set. This is interesting given that the study is being conducted in a scenario of economic crisis and most indebted clients were paying off their debts at the start of the study. This may be due to the client’s interest in normalising their status in order to perform other actions that a default might prevent.

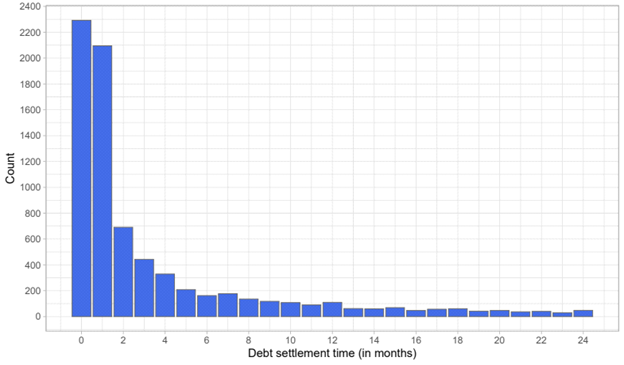
Figure 3 Debt settlement time (in months).

In Figure 4 we have the Kaplan-Meier curve estimated for the clients debt settlement times. It is possible to see a large number of censures on the right, that is, a large number of clients who did not pay off their debts within the 24-month period. Furthermore, it is important to highlight that the survival curve estimated in Figure 4 starts approximately at point 0.75, due to the presence of zero inflation in Figure 3.

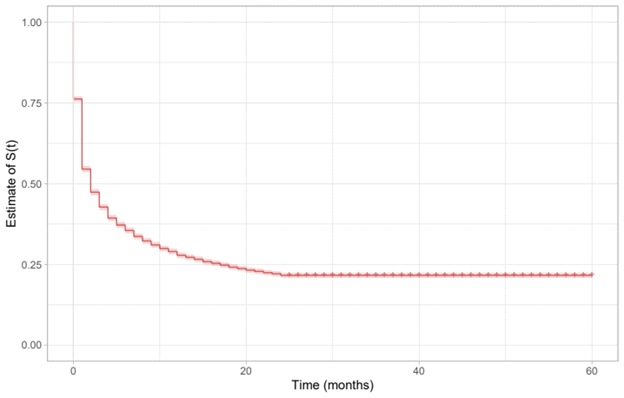
Figure 4 Survival curve for debt repayment times (in months).

The estimated Kaplan-Meier curves stratified by the categorical covariate are shown in Figure 5, where there are differences in the curves for different categories within the covariate, representing a difference in survival.

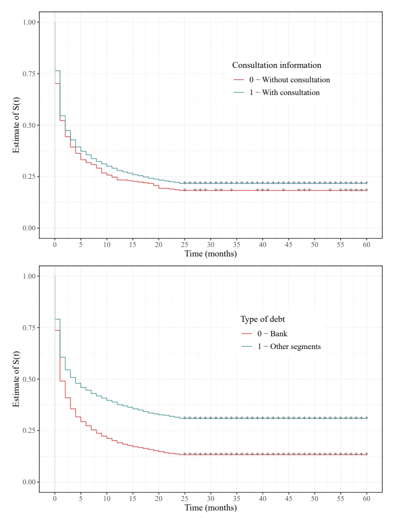
Figure 5 Estimated Kaplan-Meier curves considering covariates: Consult credit reports and segment of adquired debt.

Therefore, in Figure 5 it is possible to highlight the Debt Type covariate, in which clients who have debts in banks pay off their debts in a greater proportion when compared to debts that come from other segments. In relation to the covariate Consultation Information, it can be observed that customers who do not have consultations on their credit reports tend to prioritise paying off their debts more than those who do.

Application of the proposed model

 In this section we present the implementation of the Zero-adjusted defective model Gompertz and inverse Gaussian. The model will be adjusted in the presence of covariates separately and jointly. To select the best model, two metrics are used to measure its quality, the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC).

Thus, the goal is to evaluate whether the type of Debit and the Consulation information influence the Debt settlement time (in months). To simplify the interpretations, it should be noted that the coefficients ${\beta }_0$  , $i=1,2$ , are related to the influence of the covariates type of Debit and the Consulation information on zero inflation, while the coefficients ${\beta }_{1i}$ , $i=1,2$ , are related to the influence of the same covariates on the parameter  of the Gompertz and Inverse Gaussian distributions. So, we have the following relations, to proportion of the zeros, $p_0$  and b respectively,

$p_0\left(x\right)=\frac{\text{exp}\left\{{\beta }_{00}+x_1{\beta }_{01}+x_2{\beta }_{02}\right\}}{1+\text{exp}\left\{{\beta }_{00}+x_1{\beta }_{01}+x_2{\beta }_{02}\right\}},$

$b\left(x\right)=\text{exp}\left\{{\beta }_{10}+x_1{\beta }_{11}+x_2{\beta }_{12}\right\}.$

 where $x^{\top }=\left(x_1,x_2\right)$  is a covariate vector, where $x_1=0$  indicates Consultation information (without consultation) and $x_1=1$  (with consultation); $x_2=0$ type of debt (bank) and $x_2=1$ (other segments) and ${\beta }_0^{\top }=\left({\beta }_{00},{\beta }_{01},{\beta }_{02}\right)$  and ${\beta }_1^{\top }=\left({\beta }_{10},{\beta }_{11},{\beta }_{12}\right)$  and their regression coefficients, respectively.

Adjustment of the model without the effect of covariates: Table 3 shows the results of the parameter estimates (MLE), standard errors (SE) and  confidence intervals obtained by fitting the zero-adjusted Gompertz and inverse Gaussian models, respectively, without the presence of covariates. It is important to note that all parameters are significant at the  significance level, as the confidence intervals do not include the zero value. We can see that the estimates of the parameters associated with the proportion of zeros ($p_0$ ) are very close for both models. Also can be noted that the cure rate found for the Gompertz model is higher than for the Inverse Gaussian model with respect to the cure rate parameter ($p_1$ ).

Figure 6 shows the adjustment of the defective zero-adjusted Gompertz (a) and Inverse Gaussian (b) models, respectively, without the presence of covariates. In this sense, it is possible to verify that the Gompertz model (a) obtained a better fit than the inverse Gaussian model (b), since the survival curve estimated by the Gompertz model is very close to the Kaplan-Meier curve.

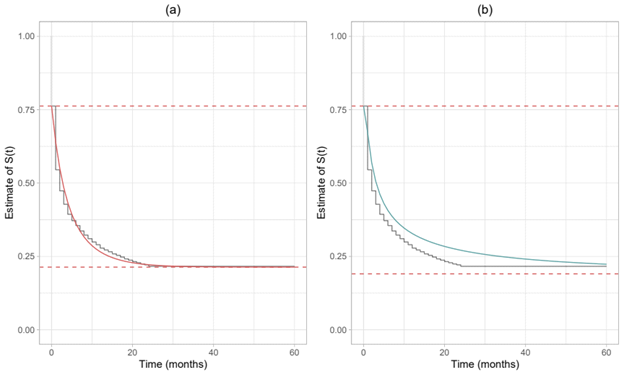
Figure 6 Kaplan-Meier estimate and the survival curve estimated by the Gompertz Adjusted Zero Defective Model (a) and Gaussian-Inverse Adjusted Zero Defective Model (b), without the presence of a covariate.

By analysing the survival functions represented by equations and, it is possible to establish a relationship with the population accumulated risk function, where ${\widehat{H}}_{pop}\left(t\right)=-\text{log}\left({\widehat{S}}_{pop}\left(t\right)\right)$ .

Figure 7 shows the estimated curves of the cumulative risk function for each of the models. In this sense, the when analysing the Gompertz model showed the best fit to the data, we can observe that there is a greater risk that the individual who acquired a debt has a greater chance of paying it off by month , as the estimated cumulative curve stabilises shortly after this point. However, it is worth noting that the risk is almost the same if the debt is repaid in up to 35 months or up to 60 months.

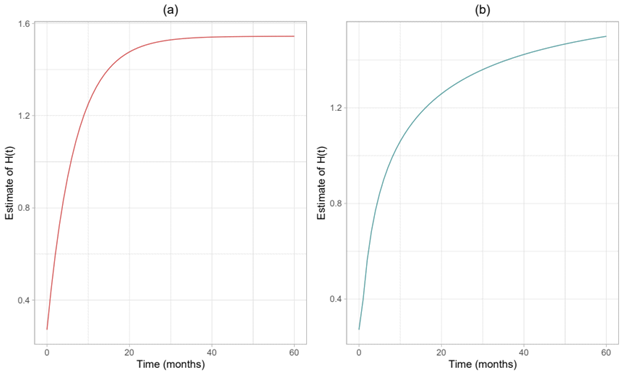
Figure 7 Estimation of the cumulative risk function (H(t)) by the Gompertz Adjusted Zero Defective Model (a) and Gaussian-inverse adjusted zero defective model (b), without the presence of a covariate.

Adjustment of the model by considering each covariate separately: Table 4 shows the parameter estimates, standard errors and theirconfidence intervals for the covariates "Consultation information" and "type of debt" for each of the proposed models. "It is also possible to observe that all the parameters of the models adjusted considering the Debt Type covariate are significant, since the confidence intervals established in both models do not include the value zero.

For the covariate "Consultation information", it can be seen that the estimates of the parameters associated with the proportion of zeros ($p_{00}$ ) are very close for both models, indicating that this covariate has a greater inflation of zeros $p_{00}=0.298$  for customers who have not received any consultation from companies on their credit report. In terms of the cure rate, the highest cure rate is given by modelling using the Gompertz distribution $p_{11}=0.214$  for clients who received consultations from companies on their credit report, while the lowest cure rate is given by modelling using the Inverse Gaussian distribution $p_{10}=0.177$  for clients who did not receive any consultation.

For the covariate "type of debt", in the table 4, can also be seen that the estimates of the parameters associated with the proportion of zeros ($p_{00}$ ) are very close for both models. In this case, the variable "type of debt" has a higher inflation of zeros $p_{00}=0.263$  for clients with bank debts, while the lower inflation of zeros $p_{01}=0.209$  for clients with debts from other segments. Furthermore, in both models, the highest proportion of cure is given to clients with debts to other segments, while the lowest proportion of cure is given to clients with debts to banks.

Figure 8 shows the survival curve estimated by the defective zero-adjusted Gompertz (a) and Inverse-Gaussian (b) models, respectively, with the presence of the covariate consultation Information on credit reports. It can be seen that the Gompertz model provides a better fit to the data than the inverse Gaussian model. The emphasis on the Gompertz model is due to the fact that its estimated survival curve is significantly close to the Kaplan-Meier estimated survival curve.

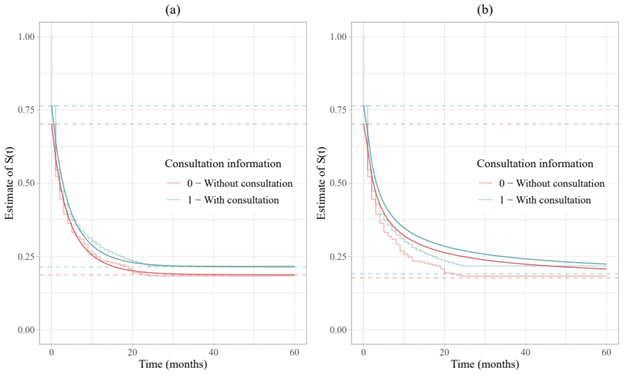
Figure 8 Kaplan-Meier estimate and the survival curve estimated by the defective Zero- Adjusted Gompertz model (a) and defective Zero-Adjusted Gaussian-Inverse model (b), with the presence of the covariate information from checking credit reports.

Figure 9 shows the estimated curves of the population cumulative risk function, ${\widehat{H}}_{pop}\left(t\right)$ , for each of the models. We can observed that the risk of an individual repaying their debt at a given point in time is greater for clients who have not had any consultation on their credit reports.

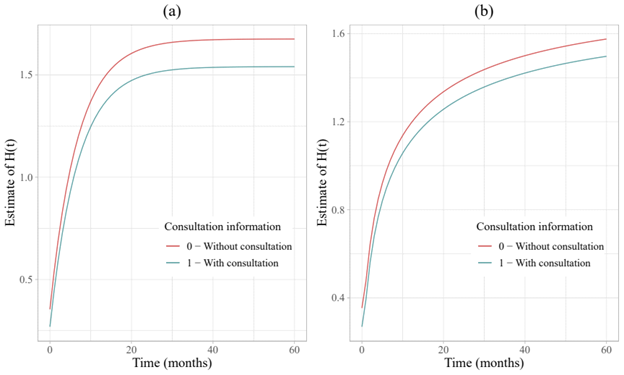
Figure 9 Estimation of the accumulated risk function (H(t)) by the defective Zero-Adjusted Gompertz model (a) and the defective Zero-Adjusted Gaussian-Inverse model (b), with the presence of the covariate Information from consultation credit reports.

Figure 10 shows the survival curve estimated by the defective zero-adjusted Gompertz (a) and Inverse-Gaussian (b) models, respectively, for the debt type covariate. It is possible to verify that the best fit occurs in the Gompertz model compared to the Inverse Gaussian model.

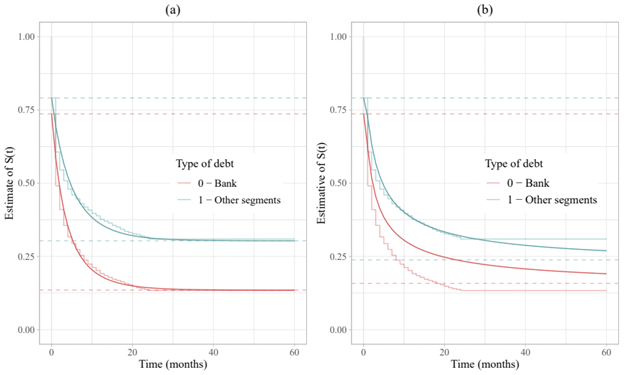
Figure 10 Kaplan-Meier estimate and the survival curve estimated by the defective Zero- Adjusted Gompertz model (a) and defective Zero-Adjusted Gaussian-Inverse model (b), with the presence of the covariate debt type.

Figure 11 shows the estimated curves of the population accumulated risk function,${\widehat{H}}_{pop}\left(t\right)=-\text{log}\left({\widehat{S}}_{pop}\left(t\right)\right)$ , for each of the models, considering the covariate Type of Debt. In this sense, can be seen that the risk of an individual repaying his debt at a given time is higher for clients who owe money to the financial sector, i.e. to banks. On the other hand, the risk that an individual will repay his debt in a given period is lower for clients with debts in other segments.

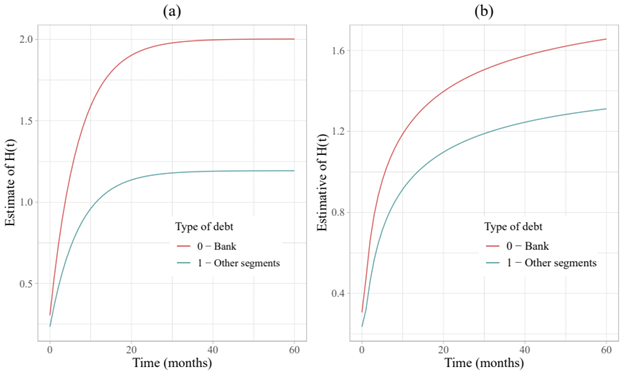
Figure 11 Estimation of the accumulated risk function (H(t)) by the defective Zero-Adjusted Gompertz model (a) and the defective Zero-Adjusted Gaussian-Inverse model (b), with the presence of the covariate debt type.

Adjustment of the model with the presence of covariates jointly: Table 5 shows the adjustment of the Gompertz and Inverse Gaussian zero-adjusted defective models, considering both covariates. It is observed that the parameters associated with the Gompertz and Inverse Gaussian distributions are significant, in addition it is verified that the majority of the estimates of the regression parametersassociated with the parameterand the proportion of zero are significant, considering the same criteria for trust regions observed in previous models.

The Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) for model selection show that the Gompertz zero-adjusted defective model is the most appropriate, as it presents the lowest AIC and BIC values. Thus, in Table 6, we present the estimates of the zero proportions and cure proportions for the zero-adjusted Gompertz defective model for the covariates consultation information and debt type. In this context, it is possible to observe from Table 6 that the highest proportion of individuals who regularise their debts at time zero is associated with customers who have not had their credit reports consulted by companies and who have debts in the financial segment i.e. banks, with a proportion of $p_{000}=0.3267$ . On the other hand, the lower proportion of individuals paying off their debts at time zero is associated with customers who have had their credit reports checked and who have debts from other segments.

It is also worth noting that clients whose credit reports have been consulted by a company and who have debts from other segments are those with the highest concentration of people who have not paid their debts within the 24-month period, as the cure rate is given by $p_{111}=0.3041$ . With regard to clients whose credit reports have not been consulted by any company and who have debts from banks, it is important to note that they have the smallest amount of outstanding debts, as the cure proportion is $p_{100}=0.1173$ . If we compare the results obtained by Toledo et al.,¹⁶ and the results in Table 6, we can see that the estimates of the proportions of zeros and cure are quite similar, which highlights the effectiveness of the model. It is important to highlight that the methodology used in this study has the advantage of only having to estimate the parameters of the defective model and the proportion of zeros ($p_0$ ), whereas in the other methodology it was necessary to estimate the proportion of zeros ($p_0$ ), the cure rate ($p_1$ ) and the parameters of the basic survival models. Finally, through Table 6, it was observed which patterns of clients tend to pay or not pay their debts within the 24-month period, using the Gompertz zero-adjusted defective model.

In this study, statistical survival models called Zero-adjusted defective regression models were studied. These models have two main characteristics that differentiate them from usual survival models: the incorporation of a portion of individuals who do not present the event of interest, even after a long period of follow-up, and also the possibility that a proportion of the times under study are equal to zero. To illustrate the modelling presented here, we analysed survival data from a real database of clients who acquired debt between the months of July and December 2015, provided by Serasa Experian, a leading institution in credit information and services in Brazil. The model made it possible to estimate the proportions of three groups of clients in a given dataset: a group in which time equals zero (clients who paid off their debts at time zero and immediately regained the ability to pay); another group of clients susceptible to the interest event (clients who paid off their debts over time and then regained the ability to pay); and a group of clients not susceptible to the event (clients who did not pay off their debts).

The results showed that the Gompertz zero-adjusted defective model performed better. The criteria used to select the best model were measured by AIC and BIC.However, it is important to emphasise that the real performance of the models presented here can be assessed in the light of their daily use by companies, using a greater variety of available data and covariates, since the model allows the use of as many covariates as necessary, whether continuous or categorical. Furthermore, it was found that the modelling presented here is similar to the modelling of the zero-adjusted cure rate models studied by Toledo et al.,⁵ However, zero-adjusted defective models have a significant advantage, as they require the estimation of one less parameter, the parameters of the defective model and the proportion of zeros, i.e. the proportion of clients who paid off their debts at the beginning of the study.

At the end of this study, it was found that it is possible to gain additional knowledge, leading to the conclusion that we can use the survival analysis technique to estimate and select an efficient model in customer portfolios with access to credit, such as those of large banks or retailers.

None.

The authors declare that they have no conflicts of interest.

1. Tsodikov AD, Yakovlev AY, Asselain B. Stochastic models of tumor latency and their biostatistical applications. World Scientific. 1996;1.
2. Boag JW. Maximum likelihood estimates of the proportion of patients cured by cancer therapy. Journal of the Royal Statistical Society. Series B (Methodological). 1949;11(1):15–53.
3. Berkson J, Gage RP. Survival curve for cancer patients following treatment. Journal of the American Statistical Association. 1952;47(259):501–515.
4. Rodrigues J, Cancho VG, de Castro M, et al. On the unification of long-term survival models. Statistics & Probability Letters. 2009;79(6):753–759.
5. Toled JS, Tomazella VLD, Lima CMM, et al. Gompertz zero-inflated cure rate regression models applied to credit risk data. Applied Stochastic Models in Business and Industry. 2023;39(2):177–197.
6. Granzotto DCT. Seleção de modelos de tempos com longa-duração para dados de finanças. 2008.
7. Balka J, Desmond AF, McNicholas PD. Bayesian and likelihood inference for cure rates based on defective inverse gaussian regression models. Journal of Applied Statistics. 2011;38:127–144.
8. Rocha R, Nadarajah S, Tomazella V, et al. A new class of defective models based on the marshall–olkin family of distributions for cure rate modeling. Computational Statistics & Data Analysis. 2017;107:48–63.
9. Scudilio J, Calsavara VF, Rocha R, et al. Defective models induced by gamma frailty term for survival data with cured fraction. Journal of Applied Statistics. 2019;46(3):484–507.
10. Calsavara VF, Rodrigues AS, Rocha R, et al. Defective regression models for cure rate modeling with interval-censored data. Biom J. 2019;61(4):841–859.
11. Ibrahim J, Chen M, Sinha D. Bayesian survival analysis. Statistics. 2014.
12. Feller W. An introduction to probability theory and its applications. John Wiley & Sons. 1991.
13. Gieser PW, Chang MN, Rao P, et al. Modelling cure rates using the gompertz model with covariate information. Stat Med. 1998;17(8):831–839.
14. Lee MLT, Whitmore GA. Threshold regression for survival analysis: modeling event times by a stochastic process reaching a boundary. Statist Sci. 2006;21(4):501–513.
15. Calsavara VF, Rodrigues AS, Rocha R, et al. Zero-adjusted defective regression models for modeling lifetime data. Journal of Applied Statistics. 2019;46(3):2434–2459.
16. Oliveira RM, Moreira F, Louzada F. The zero-inflated promotion cure rate model applied to financial data on time-to-default. Cogent Economics & Finance. 2017;5(1):1395950.