The stochastic natures of lifetime data are really a challenge for statistician to search a suitable distribution for modeling and analysis of lifetime data. Keeping in mind the stochastic natures of lifetime data, a new lifetime distribution named Uma distribution has been suggested. Its several statistical properties, estimation of parameter and applications have been discussed. Applications of the distribution have been presented with three datasets and the goodness of fit of Uma distribution has been compared with exponential, Lindley, Shanker, Akash and Sujatha distributions.

Keywords: lifetime distributions, statistical properties, estimation of parameter, applications

Due to stochastic nature of lifetime data, the search for lifetime distribution in the field of lifetime data analysis is expanding exponentially and getting popularity among policy makers to model data. In recent decades several lifetime distributions have been suggested in statistics literature. For example, Lindley distribution by Lindley,¹ Shanker distribution by Shanker,² Akash distribution by Shanker,³ and Sujatha distribution by Shanker,⁴ is some among others. Shanker et al.⁵ discussed the modeling of lifetime data using exponential and Lindley distributions and observed that there are some datasets in which these two distributions do not give good fit. Further, Shanker et al.⁶ put an effort to have comparative study on modeling of lifetime data using exponential, Lindley and Akash distribution and found that Akash distributions gives much better fit than both exponential and Lindley distribution but still there are some data sets in which these three distributions do not give good fit. Then, Shanker and Hagos,⁷ tried to model the real lifetime datasets using exponential, Lindley, Shanker and Akash and observed that still there are some datasets in which these distributions do not give good fit. Flexibility and tractability are the two important characteristics of a lifetime distributions and if the existing distributions are not flexible or tractable for the given dataset, then the search for a new distribution starts. Sometimes, data are being transformed to satisfy some assumptions of the distribution so that distribution fits well. But this is not useful practice because the original nature of the dataset is lost. Therefore, the most preferable is to search a distribution which fits the given data well than to modify the existing distributions.

While testing the goodness of fit of some well-known one parameter lifetime distributions available in literature, it has been observed that the existing distributions do not fit the data well. In this paper, in the search for a new distribution, we propose a new distribution named Uma distribution which fits the data well over the existing distributions. The statistical properties, estimation of

parameter and applications of the distribution has been presented systematically. It is hoped and expected that the distribution will draw attention of researchers to model lifetime data and preferred over the existing one parameter lifetime distributions.

Taking the convex combination of exponential $\left(\theta \right)$ , gamma $\left(2,\theta \right)$ and gamma $\left(4,\theta \right)$ with respective mixing proportions $\frac{{\theta }^3}{{\theta }^3+{\theta }^2+6},\frac{{\theta }^2}{{\theta }^3+{\theta }^2+6}$ and , $\frac{6}{{\theta }^3+{\theta }^2+6}$ a probability density function (pdf) can be expressed as

We would call this distribution as ‘Uma distribution’. Since it is a convex combination of exponential and gamma distributions, it is expected to give better fit over exponential and gamma distribution and other distributions developed using convex combinations of exponential and gamma distribution. The cumulative distribution function (cdf) of Uma distribution can be obtained as

The behaviour of the pdf and the cdf of Uma distribution for varying values of parameter $\theta$ have been presented in Figures 1,2 respectively.

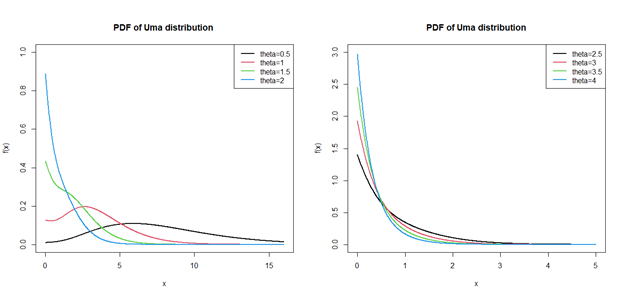
Figure 1 Graphs of the pdf of Uma distribution for selected values of the parameter.

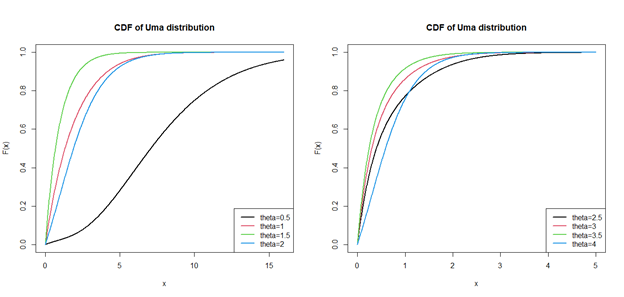
Figure 2 Graphs of the cdf of Uma distribution for selected values of the parameter.

• Hazard rate function

The hazard rate function of a random variable $X$ having pdf $f\left(x;\theta \right)$ and cdf $F\left(x;\theta \right)$ is defined as

Thus, the hazard rate function of Uma distribution can be obtained as

This gives. $h\left(0\right)=\frac{{\theta }^4}{{\theta }^3+{\theta }^2+6}=f\left(0\right)$ The behaviour of the hazard rate function of Uma distribution for various values of parameter is shown in the following Figure 3.

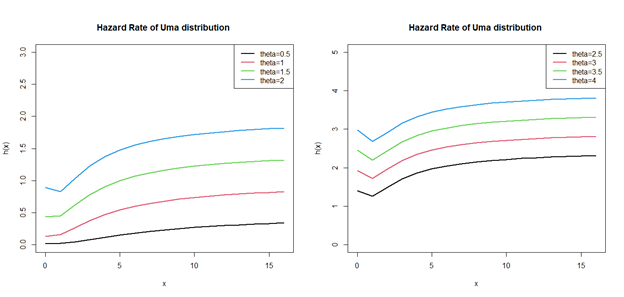
Figure 3 Graphs of the hazarad rate function of Uma distribution for selected values of the parameter.

• Mean residual life function

Let $X$ be a random variable over the support $\left(0,\infty \right)$ representing the lifetime of a system. Mean Residual life (MRL) function measures the expected value of the remaining lifetime of the system, provided it has survived up to time. Let us consider the conditional random variable $X_x=\left(X-x|X>x\right);x>0$ . Then, the MRL function, denoted by, $m\left(x\right)$ is defined as

The MRL function of Uma distribution can thus be obtained as

This gives$m\left(0\right)=\frac{{\theta }^3+2{\theta }^2+24}{\theta \left({\theta }^3+{\theta }^2+6\right)}={\mu }_1{}^{\prime }$ . The behaviour of the mean residual life function of Uma distribution for various values of parameter $\theta$ is shown in the following Figure 4.

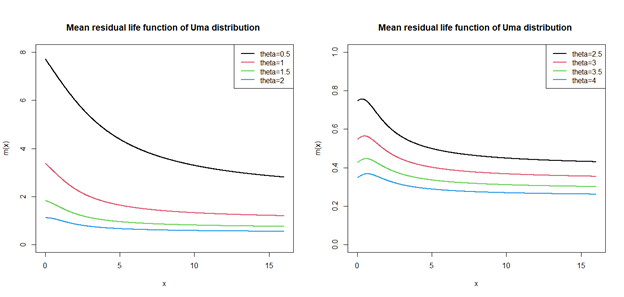
Figure 4 Graphs of the mean residual life function of Uma distribution for selected values of the parameter.

The reverse hazard rate of a random variable $X$ having pdf $f\left(x;\theta \right)$ and cdf $F\left(x;\theta \right)$ is defined as

Thus, the reverse hazard rate function of Uma distribution can be obtained as$h_r\left(x\right)=\frac{{\theta }^4\left(1+x+x^3\right)e^{-\theta x}}{\left({\theta }^3+{\theta }^2+6\right)-\left[\left({\theta }^3+{\theta }^2+6\right)+\theta x\left({\theta }^2{x}^2+3\theta x+{\theta }^2+6\right)\right]e^{-\theta x}}$

 Mill’s ratio of a random $X$ xmlns='http://www.w3.org/1998/Math/MathML'> X MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqkY=Mj0xXdbba91rFfpec8Eeeu0xXdbba9frFj0=OqFf ea0dXdd9vqaq=JfrVkFHe9pgea0dXdar=Jb9hs0dXdbPYxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIfaaaa@37EB@ variable having pdf $f\left(x;\theta \right)$ and cdf $F\left(x;\theta \right)$ is defined as

 Mill’s ratio$=\frac{1}{h\left(x\right)}=\frac{1-F\left(x;\theta \right)}{f\left(x;\theta \right)}$

Thus, the Mill’s ratio of Uma distribution can be obtained as$\frac{1}{h\left(x\right)}=\frac{{\theta }^3\left(x^3+x+1\right)+{\theta }^2\left(3x^2+1\right)+6\theta x+6}{{\theta }^4\left(1+x+x^3\right)}$

Stochastic ordering

In Probability theory and statistics, a stochastic order quantifies the concept of one random variable being bigger than another. A random variable  is said to be smaller than a random variable  in the

1. Stochastic order $\left(X{\le }_{st}Y\right)$ for all$x$
2. Hazard rate order $\left(X{\le }_{hr}Y\right)$ if $h_X\left(x\right)\ge h_Y\left(y\right)$ for all$x$
3. Mean residual life order $\left(X{\le }_{mrl}Y\right)$ if $m_X\left(x\right)\ge m_Y\left(y\right)$ for all$x$
4. Likelihood ratio order $\left(X{\le }_{lr}Y\right)$ if $\frac{f_X\left(x\right)}{f_Y\left(y\right)}$ decrease in$x$

The following results due to Shaked and Shantikumar,⁸ are well known for establishing stochastic ordering of distributions$\underset{\begin{array}{l}\Downarrow \\ X{<}_{st}Y\end{array}}{X{<}_{lr}Y\Rightarrow X{<}_{hr}Y\Rightarrow X{<}_{mrl}Y}$

Theorem: Let $X~$ Uma distribution $\left({\theta }_1\right)$ and $Y~$ Uma. $\left({\theta }_2\right)$ If ${\theta }_1>{\theta }_2$ , then $X{<}_{lr}Y$ hence $X{<}_{hr}Y$ ,$X{<}_{mrl}Y$ and $X{<}_{st}Y$ .

Proof: We have

We have ,$\log \left[\frac{f_X\left(x\right)}{f_Y\left(x\right)}\right]=\log \left[\frac{{\theta }_1{}^4\left({\theta }_2{}^3+{\theta }_2{}^2+6\right)}{{\theta }_2{}^4\left({\theta }_1{}^3+{\theta }_1{}^2+6\right)}\right]-({\theta }_1-{\theta }_2)x$

Therefore,$\frac{d}{dx}\log \left[\frac{f_X\left(x\right)}{f_Y\left(x\right)}\right]=-({\theta }_1-{\theta }_2)$

Thus, for ${\theta }_1>{\theta }_2$ ,$\frac{d}{dx}\log \left[\frac{f_X\left(x\right)}{f_Y\left(x\right)}\right]<0$ . this means that $X{<}_{lr}Y$ hence $X{<}_{hr}Y$ ,and $X{<}_{st}Y$ .

The $r$ th moment about origin ${\mu }_r{}^{\prime }$ of Uma distribution can be obtained as ${\mu }_r{}^{\prime }=E\left(X^r\right)=\frac{{\theta }^4}{{\theta }^3+{\theta }^2+6}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^r\left(1+x+x^2\right)}{e}^{-\theta x}dx$

Substituting $r=1,2,3,4$ in the above equation, the first four moments about origin of Uma distribution can be obtained as

${\mu }_1{}^{\prime }=\frac{{\theta }^3+2{\theta }^2+24}{\theta \left({\theta }^3+{\theta }^2+6\right)}$ ,${\mu }_2{}^{\prime }=\frac{2\left({\theta }^3+3{\theta }^2+60\right)}{{\theta }^2\left({\theta }^3+{\theta }^2+6\right)}$

${\mu }_3{}^{\prime }=\frac{6\left({\theta }^3+4{\theta }^2+120\right)}{{\theta }^3\left({\theta }^3+{\theta }^2+6\right)}$ ,${\mu }_4{}^{\prime }=\frac{24\left({\theta }^3+5{\theta }^2+210\right)}{{\theta }^4\left({\theta }^3+{\theta }^2+6\right)}$ .

The moments about the mean, using relationship between moments about the mean and the moments about the origin, can thus be obtained as

The descriptive constants including coefficient of variation (CV), coefficient of skewness (CS), coefficient of kurtosis (CK) and the index of dispersion (ID) of Uma distribution are thus obtained as

Behaviour of coefficient of variation, coefficient of skewness, coefficient of kurtosis and index of dispersion for changing values of parameter are shown in the Figure 5.

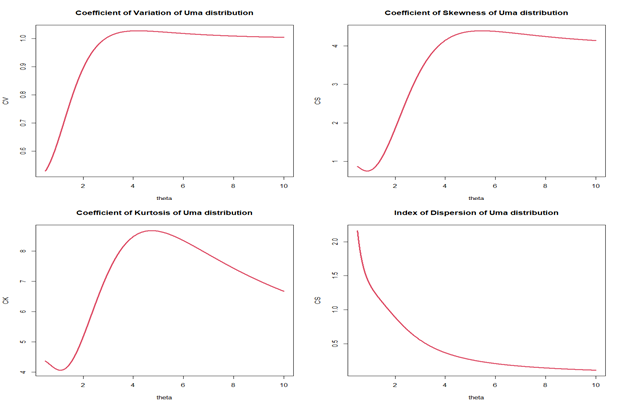
Figure 5 Graph of CV, CS, CK and ID of Uma distribution for different values of the parameter.

Mean deviation about the mean and the mean deviation about median of a random variable $X$ having pdf $f\left(x\right)$ and cdf $F\left(x\right)$ are defined by${\delta }_1(x)={\displaystyle \underset{0}{\overset{\infty }{\int }}|x-\mu |f(x)dx}=2\mu F(\mu )-2{\displaystyle \underset{0}{\overset{\mu }{\int }}xf(x)dx}$

 and ${\delta }_2(x)={\displaystyle \underset{0}{\overset{\infty }{\int }}|x-M|f(x)dx}=-\mu +2{\displaystyle \underset{M}{\overset{\infty }{\int }}xf(x)dx}$ respectively, where $\mu =E(X)$ and$M=Median(X)$ .

Using pdf and expressions for the mean of Uma distribution, we get

Using above expressions some algebraic simplifications, the mean${\delta }_1(x)$ deviation about the mean, and the mean deviation about the median ${\delta }_2(x)$ of Uma distribution are obtained as${\delta }_1(x)={\frac{2\left[{\theta }^3{\mu }^3+6{\theta }^2{\mu }^2+{\theta }^3\mu +18\theta \mu +\left({\theta }^3+2{\theta }^2+24\right)\right]e}{\theta \left({\theta }^3+{\theta }^2+6\right)}}^{-\theta \mu }$ ${\delta }_2\left(x\right)={\frac{2\left[{\theta }^4\left(M^4+M^2+M\right)+{\theta }^3\left(4M^3+2M+1\right)+2{\theta }^2\left(6M^2+1\right)+24\left(\theta M+1\right)\right]e}{\theta \left({\theta }^3+{\theta }^2+6\right)}}^{-\theta M}-\mu$

Suppose $\left(x_1,x_2,x_3,\mathrm{...},x_n\right)$ be a random sample of size $n$ from Uma distribution. The log likelihood function, $L$ of Uma distribution is given by

The maximum likelihood estimate (MLE) $\left(\widehat{\theta }\right)$ of the parameters $\left(\theta \right)$ of Uma distribution is the solution of the following log likelihood equation

This gives

This is a fourth degree polynomial equation in $\theta$ . It should be noted that the method of moment estimate is also the same as that of the MLE. The above equation can easily be solved using Newton-Raphson method, taking the initial value of the parameter$\theta =0.5$ .

The applications and the goodness of fit of Uma distribution has been discussed with three datasets. Keeping in mind the flexibility and tractability of the distribution with the dataset following three datasets have been considered.

Data set 1: This data set represents the lifetime data relating to relief times (in minutes) of 20 patients receiving an analgesic and reported by Gross and Clark.⁹

1.1, 1.4, 1.3, 1.7, 1.9, 1.8, 1.6, 2.2, 1.7, 2.7, 4.1, 1.8, 1.5, 1.2, 1.4, 3, 1.7, 2.3, 1.6, 2.0

Data Set 2: This data set is the strength data of glass of the aircraft window reported by Fuller et al.¹⁰:

18.83, 20.80, 21.657, 23.03, 23.23, 24.05, 24.321, 25.5, 25.52, 25.80, 26.69, 26.77, 26.78, 27.05, 27.67, 29.90, 31.11, 33.2, 33.73, 33.76, 33.89, 34.76, 35.75, 35.91, 36.98, 37.08, 37.09, 39.58, 44.045, 45.29, 45.381

Data Set 3: The following data represent the tensile strength, measured in GPa, of 69 carbon fibers tested under tension at gauge lengths of 20 mm(Bader and Priest, 1982)¹¹:  

1.312, 1.314, 1.479, 1.552, 1.700, 1.803, 1.861, 1.865, 1.944, 1.958, 1.966, 1.997, 2.006, 2.021, 2.027, 2.055, 2.063, 2.098, 2.140, 2.179, 2.224, 2.240, 2.253, 2.270, 2.272, 2.274, 2.301, 2.301, 2.359, 2.382, 2.382, 2.426, 2.434, 2.435, 2.478, 2.490, 2.511, 2.514, 2.535, 2.554, 2.566, 2.570, 2.586, 2.629, 2.633, 2.642, 2.648, 2.684, 2.697, 2.726, 2.770, 2.773, 2.800, 2.809, 2.818, 2.821, 2.848, 2.880, 2.954, 3.012, 3.067, 3.084, 3.090, 3.096, 3.128, 3.233, 3.433, 3.585, 3.585 .

The values ML estimates of parameter, , AIC (Akaike Information Criterion), AICC (Akaike Information Criterion corrected), BIC (Bayesian Information criterion), K-S (Kolmogorov-Smirnov) for the considered distributions for the given datasets have been computed and presented in Tables 1–3 respectively.

It is clear from the goodness of fit in the Tables 1 to 3 that Uma distribution gives much better fit over exponential, Lindley, Shanker, Akash and Sujatha distributions.

A new lifetime distribution named Uma distribution has been suggested. Statistical properties, estimation of parameter and applications of the distribution has been presented. As the distribution is new one, it is expected and hoped that it will be of great use to statisticians working in the field of modeling lifetime data from different fields of knowledge.

Being a new lifetime distribution with flexibility, tractability and practicability, a lot of future works can be done on Uma distribution.

Author is really grateful to the Editor-In-Chief of the Journal and the anonymous reviewer for quick and valuable comments on the paper.

There aren't any conflict of interests.

None.

1. Lindley DV. Fiducial distributions and Bayes’ theorem. Journal of the Royal Statistical Society, Series B. 1958;20:102–107.
2. Shanker R. Shanker distribution and its applications. International Journal of Statistics and Applications. 2015a;5(6):338–348.
3. Shanker R. Akash Distribution and its applications. International Journal of Probability and Statistics. 2015b;4(3):65–75.
4. Shanker R. Sujatha Distribution and its applications. Statistics in Transition-New series. 2016a;17(3):391–410.
5. Shanker R, Hagos F, Sujatha S. On Modeling of Lifetimes data using Exponential and Lindley distributions. Biom Biostat Int J. 2015;2(5):140–147.
6. Shanker R, Hagos F, Sujatha S. On modeling of lifetime data using one parameter Akash, Lindley and exponential distributions. Biom Biostat Int J. 2016;3(2):54–62.
7. Shanker R, Hagos F. On modeling of lifetime data using Akash, Shanker, Lindley and exponential distributions. Biom & Biostat Int J. 2016;3(6):214–224.
8. Shaked M, Shanthikumar JG. Stochastic Orders and Their Applications. Academic Press, New York: 1994.
9. Gross AJ, Clark VA. Survival Distributions: Reliability Applications in the Biometrical Sciences. New York: John Wiley. 1975.
10. Fuller EJ, Frieman S, Quinn J, et al. Fracture mechanics approach to the design of glass aircraft windows: A case study, SPIE Proc 1994;2286:419–430.
11. Bader MG, Priest AM. Statistical aspects of fiber and bundle strength in hybrid composites. In: Hayashi T, Kawata K, Umekawa S, editors. Progress in Science in Engineering Composites, ICCM-IV. Tokyo; 1982:1129–1136.