Machine learning has been a trending topic for which almost every research area would like to incorporate some of the technique in their studies. In this paper, we demonstrate several machine learning models using two different data sets. One data set is the thermograms time series data on a cancer study that was conducted at the University of Louisville Hospital, and the other set is from the world-renowned Framingham Heart Study.

Thermograms can be used to determine a patient’s health status, yet the difficulty of analyzing such a high-dimensional dataset makes it rarely applied, especially in cancer research. Previously, Rai et al.¹ proposed an approach for data reduction along with comparison between parametric method, non-parametric method (KNN), and semiparametric method (DTW-KNN) for group classification. They concluded that the performance of two-group classification is better than the three-group classification. In addition, the classifications between types of cancer are somewhat challenging.

The Framingham Heart Study is a famous longitudinal dataset which includes risk factors that could potentially lead to the heart disease. Previously, Weng et al.² and Alaa et al.³ concluded that machine learning could significantly improve the accuracy of cardiovascular risk prediction. Since the original Framingham data have been thoroughly analyzed, it would be interesting to see how machine learning models could improve prediction.

In this manuscript, we further analyze both the thermogram and the Framingham Heart Study datasets with several learning models such as gradient boosting, neural network, and random forest by using SAS Visual Data Mining and Machine Learning on SAS Viya. Each method is briefly discussed along with a model comparison. Based on the Youden’s index and misclassification rate, we select the best learning model. For big data inference, SAS Visual Data Mining and Machine Learning on SAS Viya, a cloud computing and structured statistical solution, may become a choice of computing.

Keywords: machine learning, misclassification, target classification, thermo gram, time series

Currently, artificial intelligence (AI) has been discussed in a host of subjects. Similar to data mining and deep learning, machine learning serves as a core branch within the AI, and can be used widely in business, medicine, and statistics, etc. The differences between machine learning and deep learning are often confusing, and some would even think they are the same thing. In fact, they have overlaps, but are actually two different branches. Here, we will discuss and utilize machine learning. Machine learning is a modeling approach that learns and identifies patterns from data, and then makes predictions from those data, with minimal human intervention.

The interpretability of the model is trivial in machine learning, as the main focus is on predictive accuracy.⁴ To achieve a high predictive accuracy, a model with high complexity would be expected, but that does not mean that more the better. The appropriate complexity must to be chosen in order to construct a good fitting model with the best generalizability. For example, in regression models, more variables do not mean a better model fitting, as the problem of overfitting will likely exist. In contrast, if a model lacks sufficient information to show the true association, then it is underfitted.

In machine learning, data usually would be split into training data and validation data (test data is optional). Training data are used for building models in which the algorithm learns from this set of data. On the other hand, validation data are used to adjust the model which built from the training data for better generalizability, but the model does not learn from this set of data. The model that has the best performance on the validation data will be selected. In our data application examples, both data sets were split into usually 70% training and 30% validation by using random sampling when partitioning. All three methods (gradient boosting, neural network, and random forest) were performed independently for each data set. Models within each method were built based on the training data, and the best model among each method was selected based on the evaluation of the validation data. Comparison between three methods was carried out at the end based on misclassification rates. In addition, auto-tuning was not used in either application, as we only wanted to see the initial assessment of models on classification.

Since the purpose of this manuscript is to show the accuracy of three machine learning models on two data sets, specific algorithms and concepts regarding each machine learning model are not discussed in detail. Algorithms are adopted from the book The Elements of Statistical Learning: Data Mining, Inference, and Prediction and are just for reference⁵ purposes in this manuscript. Readers can refer to this book for further detail.

Thermogram data

The University of Louisville Institutional Review Board have approved the study protocol and patient consent procedures (IRB# 08.0108, 08.0636, 608.03, 08.0388). All participating patients gave written informed consent for their tissues and blood to be entered a tissue repository (IRB# 608.03, 08.0388) and utilized for research purposes. The IRB specifically approved the use of plasma specimens from the biorepository for use in this study without the need for further consent (IRB# 08.0108, 08.0636).

Plasma samples from 100 healthy individuals with known demographic characteristics were purchased from Innovative Research (Southfield, MI). Cervical cancer specimens were obtained from women with invasive cervical carcinoma attending the clinics of the Division of Gynecologic Oncology. Lung cancer specimens were obtained from patients attending the clinics of the Division of Thoracic Oncology.

The thermogram time series data contained 186 samples, of which 35 were cervical cancer, 54 were lung cancer, and 97 were normal subjects. Details regarding the collection of differential scanning calorimetry (DSC) data can be found in Rai et al.¹ For each sample, measurement of heat capacity (HC) values (cal/ °C.g) was made at every temperature point, from 45 degrees to 90 degrees, with 0.1 degree intervals. Negative values, often caused by machine reading errors among low HC values, were not compatible with models, and have been imputed with the next closest positive value to create a continuous curve. For example, if the HC values at 50, 50.1 and 50.2 degrees are 0.02, -0.01, 0.03 respectively, then we impute the negative value at 50.1 degrees with 0.03. The goal of our analysis was to make a three-group classification based on the thermogram data. Other variables were also used in the model including age, gender, and ethnicity.

Framingham heart study data

The Framingham Heart Study data is a very large set, with 5209 samples in total. In this study, our goal was to discern between heart disease and non-heart disease. We only took data from subjects who were dead and had a known cause of death. We treated both cerebral vascular disease and coronary heart disease as “heart disease”, and combined “other” and “cancer” as a second category. After initial preparation, we had 1463 samples in total. Next, we calculated the main artery pressure (MAP) by using variables of diastolic and systolic pressure. With a high MAP (>100), the patient was deemed to have hypertension. Thus, we categorized all samples into two parts: 434 dead with heart problem, and 1029 dead without heart disease. To identify a heart problem, the subject should have both hypertension and have died with heart disease. Other variables used in the model included age, medical record weight (MRW), blood pressure status, cholesterol status, and smoking status.

Gradient boosting

To understand gradient boosting, one should also know about the AdaBoost (adaptive boosting) algorithm. It is an additive model that starts with a decision tree in which every observation is given the same weight, and after the initial evaluation, the weights change depending on the difficulty to classify, and that all leads to the second tree. The new model is the combination of both trees. The algorithm of AdaBoost can be briefly written as follows:

Let Y be output variable, X be a vector of predictor variables, and G(X) be a classifier that produces a prediction.

1. Initialize the observation weights $w_i=\frac{1}{N}, i=1,2, \dots , N.$

2. For iteration $m=1$ to M

1. Fit a classifier $G_m\left(x\right)$ to the training data using weights $w_i$ .
2. Compute weighted error rate: $er{r}_m=\frac{{{\displaystyle \sum }}_{i=1}^N{w}_{i}I\left(y_i\ne G_m\left(x_i\right)\right)}{{{\displaystyle \sum }}_{i=1}^N{w}_i}.$
3. Compute ${\alpha }_m$ given to $G_m\left(x\right)$ in producing the final classifier: ${\alpha }_m=\log \left(\frac{1-er{r}_m}{er{r}_m}\right).$
4. Update the individual weights of each observation for the next iteration.

     Set $w_i\leftarrow w_i*\exp \left[ {\alpha }_m*I\left(y_i\ne G_m\left(x_i\right)\right)\right], i=1,2,\dots , N.$

3. Output $G\left(x\right)=sign\left[{{\displaystyle \sum }}_{m=1}^M{\alpha }_m{G}_m\left(x\right)\right].$

The AdaBoost is equivalent to forward stagewise additive modeling, in which the algorithm can be written as:

1. Initialize $f_o\left(x\right)=0.$
2. For $m=1 to M:$

1. Compute $\left({\beta }_m, {\gamma }_m\right)=\arg min{{\displaystyle \sum }}_{i=1}^{N}L\left(y_i, f_{m-1}\left(x_i\right)+\beta b\left(x_i; \gamma \right)\right).$
2. Set $f_m\left(x\right)=f_{m-1}\left(x\right)+{\beta }_{m}b\left(x; {\gamma }_m\right)$

where ${\beta }_m, m=1,2,\dots , M$ are the expansion coefficients, and $b\left(x_i; \gamma \right)$ are basis functions of the multivariate argument x, characterized by a set of parameters $\gamma$ to the current expansion $f_{m-1}\left(x\right)$ . The squared-error loss function can be further expressed as ${\left(y_i-f_{m-1}\left(x_i\right)-\beta b\left(x_i; \gamma \right)\right)}^2$ where $y_i-f_{m-1}\left(x_i\right)$ can be written as $r_{im}$ to represent the residual of the current model on the ith observation.

Going forward, a weak learner is introduced to compensate for the shortcomings of the existing weak learners at each stage, and the process is repeated for certain iterations. The final model thus contains the weighted sum of the predictions of all tree models. In gradient boosting, the algorithm identifies the shortcoming of the weak learners by gradient, whereas AdaBoost identifies shortcomings by high-weight data points. The gradient comes from the loss function which is a function that measures how well the predictive model fits when classifying targets. Therefore, the goal of gradient boosting is to add the learner that can maximize the correlation with the negative gradient of the loss function. The algorithm of gradient boosting for K-class classification can be expressed as follow:

Let targets y_ik coded as 1 if observation i is in class k, and zero otherwise.

1. Initialize $f_{k0}\left(x\right)=0, k=1,2, \dots , K.$
2. For $m=1 to M:$

1. Set the class conditional probabilities $p_k\left(x\right)=\frac{e^{f_k\left(x\right)}}{{{\displaystyle \sum }}_{l=1}^K{e}^{f_l\left(x\right)}}, k=1,2,\dots ,K.$
2. For $k=1 to K:$

1. Compute residual $r_{ikm}=y_{ik}-p_k\left(x_i\right), i=1,2, \dots , N.$
2. Fit a regression tree to the targets $r_{ikm}, i=1,2, \dots , N,$ giving terminal regions $R_{jkm}, \text{j}=1,2,\dots ,J_m$ .
3. Compute ${\gamma }_{jkm}=\frac{K-1}{K}\frac{{\displaystyle \sum }_{x_i\in R_{jkm}}{r}_{ikm}}{{\displaystyle \sum }_{x_i\in R_{jkm}}\left|r_{ikm}\right|\left(1-\left|r_{ikm}\right|\right)}, j=1,2, \dots ,J_m$
4. Update $f_{km}\left(x\right)=f_{k,m-1}\left(x\right)+{\displaystyle \sum }_{j=1}^{J_m}{\gamma }_{jkm}I\left(x\in R_{jkm}\right).$

3. Output ${\stackrel{⌢}{f}}_k\left(x\right)=f_{kM}\left(x\right), k=1,2,\dots , K$ .

Neural networks

In neural networks, there are at least three layers: input layer, hidden layer, and target layer. The hidden layer can be adjusted to increase accuracy and improve model fitness, but in our case, we used only one hidden layer. Within each layer, there are neurons that are connected to other neurons in other layers. The size of the neuron indicates the absolute value of the estimated weights, which shows the importance of a certain variable to the target classification. In a model for K-class classification, there are total of K units at the top of the network diagram, with the kth unit modeling the probability of class k. There are K target measurements $Y_k, k=1,\dots , K$ , each being coded as a 0 or 1 variable for the kth class. $Z_m$ is defined as the hidden unit in the neural network, and $Y_k$ is called the target that could be modeled as a function of linear combinations of $Z_m$ . $Z_m$ can be calculated from linear combinations of the inputs. These can be expressed in the following way:

$Z_m=\sigma \left({\alpha }_{0m}+{\alpha }_m^{T}X\right), m=1,\dots ,M,$

$T_k={\beta }_{0k}+{\beta }_k^{T}Z, k=1,\dots ,K,$

$f_k\left(X\right)=g_k\left(T\right), k=1,\dots ,K,$

where $Z=\left(Z_1, Z_2,\dots , Z_m\right)$ , and $T=\left(T_1, T_2,\dots , T_K\right)$ . The neural network makes a prediction based on the input variables, as it is acting more like a regression model. The activation function $\sigma \left(v\right)$ is usually chosen to be the $sigmoid \sigma \left(v\right)=\frac{1}{1+e^{-v}}.$ The output function, $g_k\left(T\right),$ allows a final transformation of the vector of outputs, T. For K-class classification, the softmax function, $g_k\left(T\right)=\frac{e^{T_k}}{{{\displaystyle \sum }}_{l=1}^K{e}^{T_l}}$ , is used. The neural network algorithm works well on almost everything regardless of the relation between inputs and outputs. Once trained, it is a great way of handling large scale of computation.

Random forests

A forest model is built up with a huge number of individual decision trees that can be treated as an ensemble. The final prediction is a combination of the predictions of the ensemble. But unfortunately, decision trees are not stable by themselves. However, with the forest model, the overall performance of the tree is still stable.⁶ Those trees are uncorrelated, which is a huge advantage when eliminating errors. In other words, when running a large number of trees, the correct trees always outperform the wrong trees. A group of trees can always produce better prediction than a single tree. The workflow of random forests can be written as follow:

1. For tree b=1 to B:

1. Draw a bootstrap sample $Z^{*b}$ of size N from the training data.
2. Grow a random forest tree $T_b$ to the bootstrapped data, by recursively repeating the following steps for each terminal node of the tree, until the minimum node size is $n_{min}$ reached.

1. Select m variables at random from the p variables.
2. Pick the best variable/split-point among the m.
3. Split the node into two daughter nodes.

2. Output the ensemble of trees ${\left\{T_b\right\}}_1^B$ .

To make a prediction at a new point x, let ${\stackrel{⌢}{C}}_b\left(x\right)$ be the class prediction of the bth random forest (rf) tree. Then ${\stackrel{⌢}{C}}_{rf}^B\left(x\right)=majority vote{\left\{{\stackrel{⌢}{C}}_b\left(x\right)\right\}}_1^B$ .

First data application--thermogram

Among the three supervising models, the Neural Network is the best model for this dataset (Table 1). The misclassification rate is 0.0545 which is slightly better than the gradient boosting model (0.0909).

In Gradient Boosting, variables with relatively higher importance are age, temperature at 50.1 degrees, temperature at 49.8 degrees, and temperature at 50.3 degrees (Figure 1). Those temperature points are the key variables when differentiating groups. The cutoff value for the receiver operating characteristic (ROC) curve is at 0.07. Similarly, in the Neural Network, the most important variables are temperatures at 49.8 degrees, 49.2 degrees, and 50.1 degrees (Figure 2). Results indicate that temperatures around 50 degrees are more relevant to the types of cancers. The cutoff value is at 0.25. The random forest model shows relatively important temperature points at 50.1 degrees, 49.8 degrees, and 50.3 degrees (Figure 3). This mostly matches the results from the other two models.  The cutoff value is at 0.33 for the ROC curve.

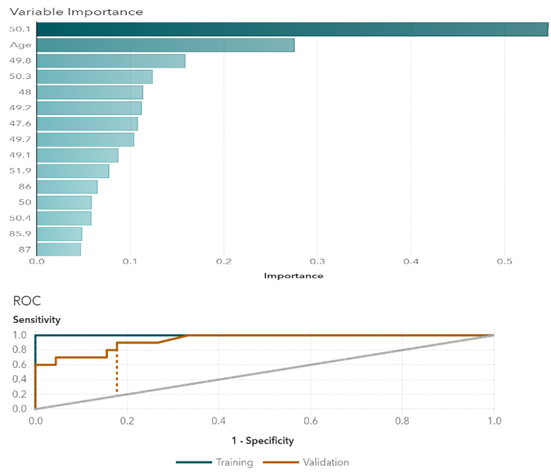
Figure 1 Gradient boosting variable importance and ROC plots.

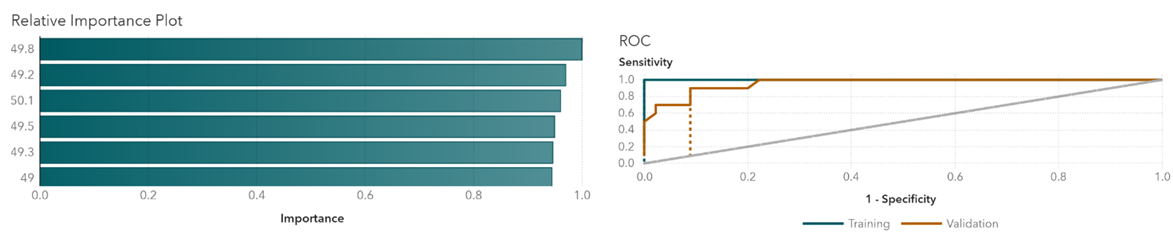
Figure 2 Neural network relative importance and ROC plots.

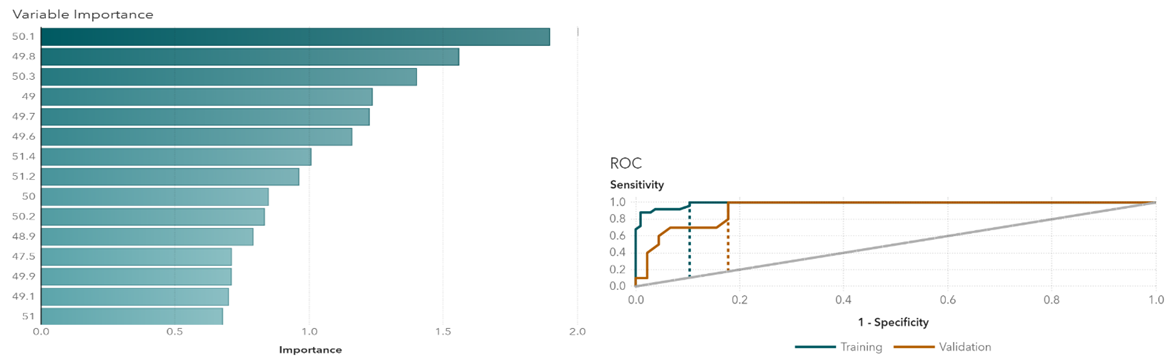
Figure 3 Random forests variable importance and ROC plots.

Second data application--framingham

Results were generated using SAS Visual Data Mining and Machine Learning on SAS Viya. To determine the best algorithm that fits the data, the misclassification rate and the Kolmogorov-Smirnov (Youden) statistic are used. The lower the misclassification rate, the better the model fits the data. One minus the misclassification rate yields the accuracy. It shows how many samples were correctly classified. On the other hand, the K-S Youden statistic is a goodness-of-fit measurement that represents the maximum distance between the ROC of the model and the ROC of the baseline. Based on the misclassification rate, Gradient Boosting is the best algorithm to fit the dataset (Table 2). The accuracy is 0.8486, which is very good. Neural Network and Random Forests also perform very well, but not as well as Gradient Boosting.

We take a closer look at each of the algorithms in detail. In Gradient Boosting, the highest impact variable is blood pressure status, which is not surprising since blood pressure is highly associated with heart disease (Figure 4). The area under the ROC curve represents the classification accuracy. The bigger the area, the better the accuracy. Dotted lines indicate K-S Youden statistics. In this model, the cutoff value is at 0.02. Neural network also confirms that blood pressure has the highest relative importance (Figure 5). The ROC curve shows that the cutoff value is at 0.34. In the random forest model, blood pressure is again the most important variable (Figure 6). The cutoff value for the ROC curve is at 0.08.

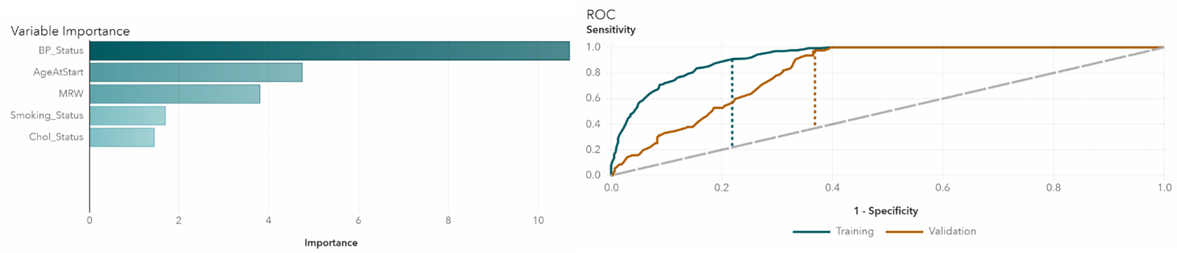
Figure 4 Gradient boosting variable importance and ROC plots.

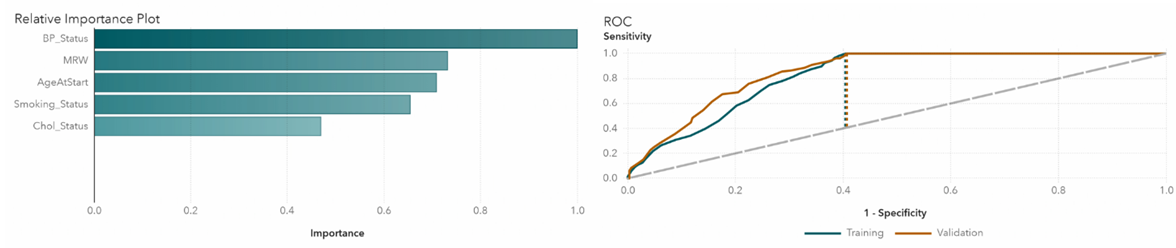
Figure 5 Neural network relative importance and ROC plots.

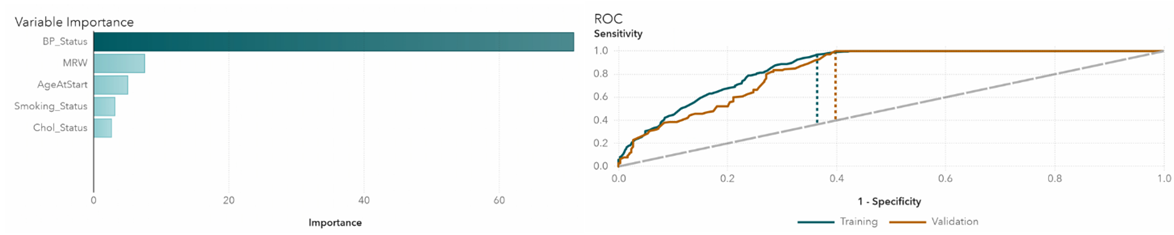
Figure 6 Random forests variable importance and ROC plots.

From both data demonstrations, all three models have proven their abilities to make high accuracy predictions. When comparing the accuracy of the first dataset to results reported in Rai et al.,¹ the difference is minimal. In fact, the Neural Network model performs better than DTW-KNN method (Table 3). However, it should be noted that the way the data were pre-processed was slightly different.

This paper only demonstrates three commonly used machine learning models on two-group and three-group classification. Future research could further extend these results to other supervising and non-supervising models on multi-group classification. In our examples, we did not use auto-tuning or use higher tree numbers to achieve a better accuracy. As always, the machine learning process is time consuming.

When making a classification, it is always used on a large-scale data set. In both of our samples, though we have lots of variables, the sample size in each group is still small.

C. Qian was supported by the National Institute of Health grant 5P50 AA024337 (CJM) and the University of Louisville Fellowship.

S. N. Rai was partly supported with Wendell Cherry Chair in Clinical Trial Research Fund and NIH grants P20GM113226 and P50AA024337 (CJM).

The authors report no conflicts of interest in this work.

1. Rai SN, Srivastava S, Pan J, et al. Multi-group diagnostic classification of high-dimensional data using differential scanning calorimetry plasma thermograms. PLoS ONE. 2019;14(8):e0220765.
2. Weng SF, Reps J, Kai J, et al. Can machine-learning improve cardiovascular risk prediction using routine clinical data? PLoS ONE. 2017;12(4):e0174944.
3. Alaa AM, Bolton T, Di Angelantonio E, et al. Cardiovascular disease risk prediction using automated machine learning: A prospective study of 423,604 UK Biobank participants. PLoS ONE. 2019;14(5):e0213653.
4. Breiman L. Random Forests. Machine Learning. 2001;45:5–32.
5. Hastie Trevor, Jerome Friedman, Robert Tisbshirani. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. New York: Springer, 2017.
6. Breiman L, Friedman J, Olshen R, et al. Classification and Regression Trees. Wadsworth, New York.1984.