An approach to the exact quantitative analysis of seed traits without using reference material is proposed basing on the quantum (discreet) nature of seed distribution is seed lots. The approach has been proven theoretically and supported experimentally with the analysis of the presence of seeds of soybean lines A2704-12, A5547-127 and GTS 40-3-2 in seed lots with the use of PCR in real-time mode tracing the transformation events. The approach may be applied not to PCR techniques only but to seed testing with whatever physical method provide the observed signal is obtained in exact values and the correlation between the signal and concentration of traced seeds is known. The approach can be of significant value in the issues of adventitious/technically unavoidable presence (AP), labeling, low level presence (LLP) and thus significantly simplify and decrease the cost of seeds breeding and trade.

GMO, genetically modified organism; CRM, certified reference material; DNA, desoxyribonucleic acid; PCR, polymerase chain reaction; low level presence; AP, adventitious presence; GM, genetically modified; FAM, 6-carboxyfluorescein; ROX, rhodamine X; MGB, minor groove binder; BHQ1, BHQ2, black hole quenchers 1 and 2; CI, confidence interval

The common and globally approved method of quantitative analysis of biotechnology traits/genetically modified organisms (GMO) is PCR in real time mode when the value of threshold cycle (C_t) of tested sample is compared with C_t values obtained through sequential dilution of the corresponding certified (standard) reference material (CRM) presented in the form of linear regression in semi-logarithmic co-ordinates C_t vs log[concentration, %].¹ There are recent developments on using digital PCR with direct DNA copy counting,² it also requires CRM though. However, certified reference materials may be quite expensive and not easily available, if available at all. Therefore, a method providing for exact quantitation of seed traits without using reference standards can be highly demanded.

ISTA (International Seed Testing Association) has developed a statistical tool (SeedCalc)³ using to assess seed purity/impurity, including level of GMO presence in conventional seed lots with qualitative testing plans using a Bayesian approach, so the results are statistical approximation. One of SeedCalc testing plans implies that a seed lot (sample) of 3000 seeds including unknown number of target seeds (seeds, that are subject to detection and differ in detected traits from the main bulk). The lot is then randomly distributed into 20 aliquots (subsamples) and the presence of target seeds is estimated basing on the number of positive aliquots (aliquots that gave positive result for the presence of target seeds).

However, real-time PCR provides exact figures for threshold cycle as the well-established function of the concentration of the tested object. Thus, we assume it is possible to make exact quantitative analysis once the exact number of target seeds in at least one aliquot or exact increment between a pair of aliquots is known. Seed lot is a discrete system, which means that the target seed content (in the seed count mode) cannot be fractional and the minimum possible content being exactly one seed. The minimum increment is also exactly one seed.

We therefore assume that within the range 1-150 target seed content per lot of 3000 seeds, randomly distributed in 20 aliquots, there will be an aliquot containing exactly one target seed or/and a pair of aliquots differing by exactly one target seed (with the probability not less than 0.95). The choice of 150 target seeds as the upper limit will be considered later in this paper, though it is more than satisfactory for the vast majority of issues related to seed purity, low level presence (LLP), adventitious presence (AP) and labeling.

Theory

For simplicity in mathematical considerations we will redefine terms seeds and aliquots so that seed=ball; target seed=red ball; non-target seed=white ball; aliquot=basket; positive aliquot (aliquot containing target seeds and showing detected trait/signal)=positive basket; negative aliquot (aliquot with zero content of target content not showing detected trait/signal)=negative basket.

Thus, the starting condition is such that there are 3000 balls composed of N red balls and (3000-N) white balls. The balls are randomly distributed into 20 baskets having 150 balls each.

Problem 1. Find probability P₁(N) for 1≤N≤150 that the basket with the lowest non-zero number of red balls contains exactly one red ball.

Problem 2. Find probability P₂(N) for 1≤N≤150, that two randomly selected baskets with a non-zero number of red balls contain n and n+1 red balls, respectively.

To enumerate ways of distributing the balls, it is convenient to consider that 3000 balls are already distributed into 20 baskets, and randomly selected N balls are the red ones. In combinatorics such a selection is called combination:⁴

$\left(\begin{array}{c}3000\\ \text{N}\end{array}\right)=\frac{3000!}{\text{N}!(3000-\text{N})!}$

Thus, total number of possible distributions $\text{Total}\left(\text{N}\right)=\left(\begin{array}{c}3000\\ \text{N}\end{array}\right)$ and this number grows quickly with N.

Similarly, the number of possible distributions of $n$ red balls to the first basket is $\left(\begin{array}{c}150\\ \text{n}\end{array}\right)$. However, the number of possible distributions of $N$ red balls when the first basket gets $n$ red balls is equal to the number of distributions of $n$ red balls to first basket multiplied by the number of distributions of $(\text{N}-\text{n})$red balls to remaining baskets: $\left(\begin{array}{c}150\\ \text{n}\end{array}\right)\left(\begin{array}{c}3000-150\\ \text{N }-\text{ n}\end{array}\right)$

Using these formulas, we can find probability $P{\text{'}}_N\left(n\right)$ that the first basket gets exactly n red balls:

${\text{P'}}_{\text{N}}\left(\text{n}\right)=\frac{\left(\begin{array}{c}150\\ \text{n}\end{array}\right)\left(\begin{array}{c}3000-150\\ \text{N }-\text{ n}\end{array}\right)}{\left(\begin{array}{c}3000\\ \text{N}\end{array}\right)}$

which is exactly hypergeometric distribution.⁵

Similarly, probability ${\text{P'}}_{\text{N}}({\text{n}}_1,{\text{n}}_2,\dots ,{\text{n}}_{\text{k}})$ that first k baskets get ${\text{n}}_1,{\text{n}}_2,\dots ,{\text{n}}_{\text{k}}$ red balls, respectively, can be calculated using the following formula:

${\text{P'}}_{\text{N}}({\text{n}}_1,{\text{n}}_2,\dots ,{\text{n}}_{\text{k}})=\frac{\left(\begin{array}{c}150\\ {\text{n}}_1\end{array}\right)\left(\begin{array}{c}150\\ {\text{n}}_2\end{array}\right)\dots \left(\begin{array}{c}150\\ {\text{n}}_{\text{k}}\end{array}\right)\left(\begin{array}{c}3000-\text{ k*}150\\ \text{N }-{\text{ n}}_1-{\text{n}}_2-\dots -{\text{n}}_{\text{k}}\end{array}\right)}{\left(\begin{array}{c}3000\\ \text{N}\end{array}\right)}$

${\text{P'}}_{\text{N}}({\text{n}}_1,\dots ,{\text{n}}_{20})=\frac{\left(\begin{array}{c}150\\ {\text{n}}_1\end{array}\right)\left(\begin{array}{c}150\\ {\text{n}}_2\end{array}\right)\dots \left(\begin{array}{c}150\\ {\text{n}}_{20}\end{array}\right)}{\left(\begin{array}{c}3000\\ \text{N}\end{array}\right)}$

(Note that this problem is different from problem of randomly distributing N red balls into 20 baskets, because the requirement of having exactly 150 balls in each basket affects resulting probability, so we cannot simply consider red balls alone and disregard white balls).

Using the previous formula, we get a simple brute-force method of calculating the probability of any event $\text{E}\left({\text{n}}_{\text{i}}\right)$, which is symmetrical (does not depend upon the order of baskets), that is:

$\text{E}(\dots ,{\text{n}}_{\text{i}},\dots ,{\text{n}}_{\text{j}},\dots )=\text{E}(\dots ,{\text{n}}_{\text{j}},\dots ,{\text{n}}_{\text{i}},\dots )$ for any :

$\text{P}\left(\text{N }|\text{ E}\right)={\sum }^{\text{}}\{{\text{P'}}_{\text{N}}({\text{n}}_1,\dots ,{\text{n}}_{20}):{\text{ n}}_1+\dots +{\text{n}}_{20}=\text{N};\text{ E}\left({\text{n}}_{\text{i}}\right)\text{ holds true}\}$

The number of terms in this formula grows exponentially so it is impractical to use it for N over 20, but we can notice that it is symmetrical with respect to permutations of ${\text{n}}_1,\dots ,{\text{n}}_{20}$. It means that we can only consider elements with ${\text{n}}_1\le {\text{n}}_2\le \dots \le {\text{n}}_{20}$ and multiply each term by the number of ways this array of can be permutated.

In case n_i numbers are all different the number of permutations will be However, if there is a group of ginumbers that are the same, we need to divide the result by (gi!) because permutations of numbers in the same group yield the same sequence $\left\{{\text{n}}_{\text{i}}\right\}$. For example, in the sequence {0,0,0,1,1,3} g1=3 (three zeroes), g₂=2 (two ones), g3=1 (one three).

Finally, if we split n1, …, n20 into groups of equal numbers, each consisting of g1, …, gk groups, then the final multiplier will be $\frac{{\displaystyle 20!}}{{\displaystyle {\text{g}}_1!\dots {\text{g}}_{\text{k}}!}}$

So, the final optimized brute force formula (master-formula) will be

$\begin{array}{l}\text{P}\left(\text{N }|\text{ E}\right)={\sum }^{\text{}}\frac{20!}{{\text{g}}_1!\dots {\text{g}}_{\text{k}}!}\text{P'}({\text{n}}_1,\dots ,{\text{n}}_{20}):\\ {\text{n}}_1+\dots +{\text{n}}_{20}=\text{N};\\ {\text{n}}_1\le {\text{n}}_2\le \dots \le {\text{n}}_{20};\\ \text{E}\left({\text{n}}_{\text{i}}\right)\text{ holds true};\\ {\text{n}}_{\text{i}}{\text{ form groups g}}_1,\dots ,{\text{g}}_{\text{k}}\text{ of same numbers}\end{array}$

Number of terms is much smaller in the optimized formula. Although exponential growth is still observed, it possible to calculate P(N|E) for N≤150 within reasonable time.

Computer calculations in exact rationales with arbitrary-precision arithmetic (https://en.wikipedia.org/wiki/Arbitrary-precision_arithmetic) were employed, thus each ${\text{P}}_{\text{I}}\left(\text{N}\right)$ was found as exact rationale $\frac{{\displaystyle \text{P}}}{{\displaystyle \text{Q}}}$, $\text{P}$ and $\text{Q}$ being arbitrary-long integers, e.g.,

$P_I\left(60\right)=\frac{{\displaystyle 849357140474701955570725932674291143871481798931223756396220646710402270220898162849890399983083873059513964034014269000}}{{\displaystyle 874008547796005305715880865842398785453190784485865613042898799660829699170076837903820651726749051888238144179924960953}}\cong 0.9718$

Calculations were done in Microsoft Visual Studio, using C# language, BigInteger (https://docs.microsoft.com/en-us/dotnet/api/system.numerics.biginteger?view=netframework-4.8) and algorithms from BigRational library https://www.nuget.org/packages/BigRationalLibrary/). The exact rationales were cast to normal floating-point numbers for the resulting data at the last stage only, thus, calculation precision was never lost.

All the exact results obtained in this work were checked with Monte Carlo method.⁶ Ten thousand random permutations of an array containing 3000 elements - (3000-N) zeroes and N ones–have been generated for each problem for each N using Fisher-Yates shuffle algorithm.⁷ Then first 150 elements of the array were assumed to be the first basket, next 150 elements being the second basket, etc. The simulated counts of the red balls n₁, …, n₂₀ were obtained by counting number of ones in each of these baskets. Then the condition was checked on n₁, …, n₂₀ , and the resulting probability was calculated as a number of positive outcomes divided by number of simulations (the latter being equal to 10000).

Results obtained with the use of the above master-formula are given in Figure 1.

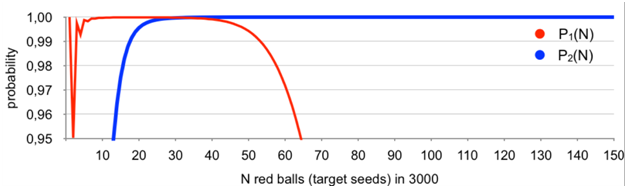
Figure 1 Probability of occurrence of a basket (aliquot) with exactly one red ball (target seed) P₁(N); probability of having an increment of exactly one red ball (target seed) between two randomly selected baskets (aliquots) P₂(N).

It is clearly seen from Figure 1 that the assumption of always having a basket (aliquot) with exactly one red ball (target seed), or/and two baskets with non-zero content differing by exactly one red ball (target seed) is correct for any 1≤N≤150. The probability never goes under 0.99 except for N=2 and never goes under 0.999 for 6≤N≤150. Indeed, two red balls can be distributed in two ways only, i.e., two balls in one basket (probability ~0.0497) and two baskets with one ball in each (probability~0,9503). Still it is above 0.95.

Figure 2 gives the range of N red balls (target seeds) occurrence as function of the nubmer of positive baskets (aliquots) observed.

Figure 2 Range of occurrence of red balls (target seeds) in positive baskets (aliquots).

N_min (0.99) and N_max (0.99) mean, that, if, for example we have 15 positive baskets, we can expect 17 to 46 red balls. Probability of finding N=16 (N_min (0.99)–1) or N=47 (N_max (0.99)+1) in 15 baskets is lower than 0.01. It can be clearly seen from Figure 2 that there is huge uncertainty in binding a particular number of positive baskets (aliquots) to the occurrence of a particular N, e.g., 30 red balls (target seeds) can be observed within the range 13–19 positive baskets (aliquots). It is obvious therefore that effective algorithm is needed to identify which basket (aliquot) or two baskets (aliquots) should be selected depending on the number of positive baskets (aliquots) observed, so the “exactly one” criterion is applied correctly.

Algorithm

Let K be the number of positive aliquots and two positive aliquots differ when the difference in their signals (Ct in the case of real-time PCR) goes beyond standard deviation values, i.e., $C_t\left(i\right)\ne C_t\left(j\right)when|C_{t\left(i\right)}-C_{t\left(j\right)}|>{\sigma }_i,{\sigma }_j$.
Sort (arrange) positive baskets (aliquots) so, that they are indexed b1, b2 …, bk, where b1 has the minimum number of the target seeds and bk–the maximum (in case of real-time PCR it means sorting from highest Ct value to lowest).

There are several special issues to be addressed at the starting point:

1. K=1, then N (total number of target seeds) is most likely 1 or 2 (with the probability below 0.05 for N=2). N>2 for one positive aliquot is most unlikely–the probability of having 3 and 4 target seeds in is less than 0.0025 and 0.000125, respectively.
2. 2≤ K≤12 and all aliquots show the same signal (Ct). Then target seeds are distributed equally by one target seed per aliquot (1,1; 1,1,1; 1,1,1,1, etc.). Probability of any other equal distribution is extremely low. Thus, for K=2 probability of 2,2 and 3,3 combinations is lower than 0.007 and 0.000125, respectively. With higher N and K, the probability of equal distribution becomes negligibly low quickly, e.g., the probability of 2,2,2,2,2 distribution for K=5 is less than 0.0002.

K = 20 and all aliquots show the same signal$\left(C_t\right)$. Then N>150.
We now shall consider the core case only, when we have a series of positive baskets (aliquots) with differing signal $(C_{t}forreal-timePCR)$values.

There are four problems to be solved:

1. Find probability $P_I\left(N\right)for1\le N\le 150$that basket b1 contains exactly one red ball.
2. Find probability $P_{II}\left(N\right)for1\le N\le 150$, that basket b1 and the next basket with the second lowest red balls content contain exactly one and two red balls, respectively.
3. Find probability $P_{III}\left(N\right)for1\le N\le 150$, that basket b1 and the next basket the second lowest red balls content contain n and (n+1) red balls, respectively
4. Define the median M as K/2. Then the pre-median basket will have index (K/2) if K is even or (K/2-0.5) when K is odd. Find probability $P_{IV}\left(N\right)for1\le N\le 150$, that the pre-median basket and the post-median basket (closest to M on the higher side and differing from the pre-median basket in red balls content) have n and (n+1) red balls, respectively (n≠0). 

This brings us to the main problem: $3000$ balls containing $N$ red balls and (3000-N) white balls are randomly distributed into 20 baskets having 150 balls each. The exact value of N (number of red balls in the 3000 balls lot) is unknown, but we consider it within the range $1\le N\le 150$.

Consider the following algorithm:

Find probability P (N) that the proposed algorithm is correct. Prove $P\left(N\right)\ge 0,95$ for any $1\le N\le 150$.

Results obtained with the use of the master-formula described earlier are given in Figures 3,4.

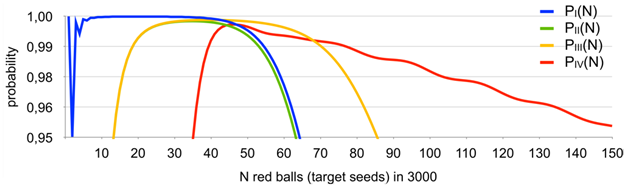
Figure 3 Probability of basket (aliquot) #1 containing exactly one red ball (target seed) - P_I(N); probability of basket (aliquot) #1 and the next basket (aliquot) with the second lowest red balls (target seeds) content containing exactly 1 and 2 red balls (target seeds), respectively - P_II(N); probability of basket (aliquot) #1 and the next basket (aliquot) with the second lowest red balls (target seeds) content containing n and (n + 1) red balls (target seeds), respectively - P_III(N); probability of the pre-median basket (aliquot) and the post-median basket (aliquot) have n and (n + 1) red balls, respectively - P_IV(N).

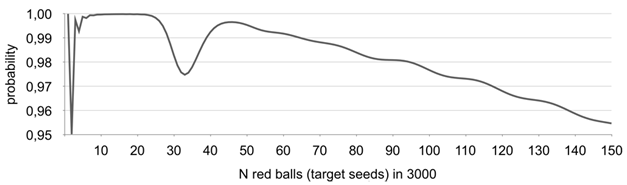
Figure 4 Probability of the proposed algorithm providing correct results - P(N).

Note the dip in the probability between N=30 to 40, relates to the fact that the probability of zero or one empty baskets is already non-negligible (2% for N=30), but P_IV(N) is still small, violating option c) of the definition of P(N) in almost 3% of all cases..

The areas of high probability intersect for the measurements:

$P_I\left(N\right)\ge 0,95for1\le N\le 65;$

$P_{II}\left(N\right)\ge 0,95for14\le N\le 64;$

$P_{III}\left(N\right)\ge 0,95for14\le N\le 85;$

$P_{IV}\left(N\right)\ge 0,95for35\le N\le 150$

are self-explanatory showing the range of possible presence of target seeds as function of the number of positive aliquots observed and give the possibility to cross-check experimental results obtained with different criteria of the algorithm above because it is obviously seen that more than one of “exactly one” criteria can be applied to the wide range of positive aliquots. Thus, both a) and b) criteria apply in case 2–16 positive aliquots, both b) and c) applies in case of 14–18 positive aliquots. And there is the special case that two aliquots with the lowest and second lowest target seed content have exactly one and two target seeds, respectively (applies to the range of 8–16 positive aliquots). This case will be discussed under “Experimental proof” below.

It clearly seen that $P\left(N\right)>0,95$ for $1\le N\le 150$. The graph is not even because different trends of $P_I\left(N\right),P_{II}\left(N\right)$ and $P_{III}\left(N\right)$ interact along with the decreasing probability of $P_I\left(N\right),P_{II}\left(N\right)$ occurrence of baskets (aliquots) with no red balls (target seeds) while N grows.

Results given in Figure 4 justify the choice of using N=150 as the upper limit in the approach since reliability of the algorithm has a trend to go below 0,95. Nevertheless, the range 1-150 target seeds in 3000 seeds (~0.03% - 5%) lot is more than enough for the vast majority of issues related to low limit presence, adventitious presence, labeling and seed purity.

Once it is proven that the presence of target seeds is exactly known for one known aliquot (or the difference in target seed content for a known pair of aliquots) we come to the equation of linear regression used in quantitative analysis. In the case of testing an aliquot with 150 seeds it is

$C_t=A•log[(n/150)•100,\%]+B$

${\text{n}}_{\text{i}}=\frac{{\displaystyle {\text{n}}_1}}{{\displaystyle {10}^{\left(\frac{{\displaystyle {\text{C}}_{\text{t}}\left(1\right)-{\text{C}}_{\text{t}}\left(\text{i}\right)}}{{\displaystyle \text{A}}}\right)}}}$

${\text{n}}_1=\frac{{\displaystyle 1}}{{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle {10}^{\left(\frac{{\displaystyle {\text{C}}_{\text{t}}\left(1\right)-{\text{C}}_{\text{t}}\left(1^{+}\right)}}{{\displaystyle \text{A}}}\right)}}}-1}}$

In case of algorithm criterion a) when there are 2–16 positive aliquots, $n_1=1and{C}_t\left(1\right)$ refer to positive aliquot #1 (sorted and $n_1=1$ ; in case of criteria b) and c) when two aliquots differing by one target seed are selected, n1 and $C_t\left(1^{+}\right)$ refer to the first aliquot of the two–it can be aliquot #1 and the pre-median aliquot. refers to the second aliquot of the chosen two, i.e., the one having one target seed more. Once calculated, n_i shall be rounded to the nearest integer value because the number of seeds cannot be fractional.

The sum of target seeds in all positive aliquots gives the content of target seeds (N) in the 3000 seeds lot

$\text{N}=\sum _{\text{i}=1}^{\text{K}}{\text{n}}_{\text{i}}$

Standard protocol of quantitative analysis with the use of real-time PCR requires that constants A (slope) and B are derived through a series of dilution of certified (standard) reference material. However, the slope value (A) depends solely on the amplified DNA sequence (amplicon), oligonucleotides (primers and probes) used for test-systems, and PCR protocol. In other words, the slope is the same for the CRM and the tested sample. In fact, quantitative analysis using CRM is based upon this principle.

The slope value is then derived through a series of sequential dilution of the most populated aliquot (self-reference calibration). Using self-calibration is justified because we deal with the systems where all target seeds are well unified discreet pieces. Direct calculations checked with Monte Carlo method show that the ratio between target seeds content in the most populated aliquot (n_max) and that in the least populated aliquot (n_min) varies within the range 3≤N≤150 however, in most cases it is hardly expected to exceed 10 up to N = 150 (~5% probability at the high end). Thus, the slope derived from dilution series in the range n_max–0.1n_max (ten-fold dilution) covers the full range of target seed presence in all positive aliquots, and 0.1n_max is always above real-time PCR detection limit (0.1%).

Seed material

Beans of genetically modified soybean (GM-soybean) lines A2704-12 (event code ACS-GMØØ5-3) and A5547-127 (event code ACS-GMØØ6-4) were provided by the FBUN “Federal Research Centre for nutrition and biotechnology” (Moscow, Russian Federation) within the framework for the development of the national technical guidelines “Detection and identification of GMO of plant origin with real-time PCR in matrix format” (MUK 4.2.3390-16) [https://www.rospotrebnadzor.ru/documents/details.php?ELEMENT_ID=8637].

Beans of GM-soybean line GTS 40-3-2 (event code MON-Ø4Ø32-6) (commodity soya beans imported from Paraguay), and non-GM soybean were provided by the “Group of Companies SODRUGESTVO” (Kaliningrad, Russian Federation).

All beans used in the experiment were calibrated to have the same weight (SD=1,5%).

DNA extraction

Blender 8010S (Waring Commercial, USA) was used to grind the beans into fine flour. 50 mg of soybean flour taken with OHAUS AP210 balance (Ohaus, Switzerland) was used for a single extraction of genomic DNA with DNA AmpliSens extraction kit DNA-sorb-C-M (FBUN “Central Research Institute of epidemiology of Rospotrebnadzor”, Moscow, Russian Federation) in accordance with the producer’s manual. DNA concentration was measured at λ=260 nm with SmartSpec Plus spectrophotometer (BioRad, USA). Purity of extracted DNA was checked by A260/A280 ratio. Extracted DNA specimens were stored at -20ºC.

Oligonucleotides

Primers and probes (with 5’-fluorescent FAM or ROX dyes) were produced by “Biotech-Industry” LLC (Moscow, Russian Federation). The probe with MGB modification was produced by Thermo Fisher Scientific (USA). All oligonucleotides used were in full compliance with JRC EC protocols, as follows:

A2704-12⁸

fwd: GCAAAAAAGCGGTTAGCTCCT;

rev: ATTCAGGCTGCGCAACTGTT;

probe: ROX-GGAAGGGCGATCGGAGGACCG-BHQ2

A5547-127⁹

fwd: CTATTTGGTGGCATTTTTCC;

rev: TGCGGCCAACTTACTTC

probe: FAM-ACAACGATGACGGTATGACATTGCGG-BHQ1

GTS 40-3-2¹⁰

fwd: TTCATTCAAAATAAGATCATACATACAGGTT;

rev: GGCATTTGTAGGAGCCACCTT;

probe: FAM–CCTTTTCCATTTGGG–MGBNFQ

PCR in real-time mode

PCR in real-time mode was carried out using the DTLite detecting thermocycler (“DNA-Technology” LLC, Moscow, Russian Federation). 25 µl of reaction mixture included 2.5µl of 10x PCR buffer, 1,2µl Mg²⁺ (50mM), 0,6 µl of dNTP (10 mM) mixture, 2µl of each of the primers (10µM), 2µl of the probe (5µM), 0,5 µl of Taq-DNA-polymerase (5 U/µl, “SibEnzym” LLC, Novosibirsk, Russian Federation), 9,2µl of deionized water, and 5µl of the specimen DNA. Pipetting was done with Sartorius Picus® electronic pipet, 0.2-10 µl (“Sartorius GMBH”, Germany).

PCR was carried out in the following mode: 50 ºC–2 min, 95 ºC–10 min, and 50 cycles of denaturation–15 sec at 95ºC and annealing+elongation–60 sec at 60ºC. Data analysis and calculation of threshold cycles was done automatically with the program software RealTime PCR v7.9 (“DNA-Technology” LLC, Moscow, Russian Federation).

Each test was carried out in five repeats and was accompanied with positive and negative control reactions, when corresponding plasmid and deionized water, respectively, was added instead of the specimen DNA.

Experiment setup

Two 3000 seed lots have been formed for the experiment

1. a) 14 beans of soybean line A27014-12+16 beans of soybean line A5547-127+2970 beans of non-GM soybean;
2. b) 150 beans of soybean line GTS 40-3-2+2850 of non-GM soybean.

Emulation of target seeds distribution

Emulation was performed using plastic balls 3 mm in diameter differing in color (black, blue and red). 3000 balls–(16 red+14 blue+2970 black) emulating the mixture of A2704-12 and A5547-127, and (150 red+2850 black) emulating GTS 40-3-2. Mixture of 3000 balls was put into an opaque bag, thoroughly mixed, then random ball was taken out “blindly” by hand (like when playing lotto) and put into one of 20 numbered (1–20) glasses. Then the balls left in the bag were mixed again. The process was repeated until all 3000 balls were distributed into 20 aliquots, containing 150 balls each.

Forming the aliquots

Since all the seed material was commodity soybean, seeds were selected to have the same weight (± 5%). Each seed was crushed into fine flour individually with pestle and mortar, genomic DNA was extracted from 50 mg of the flour and tested for the presence of the target transformation event.  The flour from selected seed was combined in one batch and thoroughly mixed. Then 100 mg of the flour was defined as 1 seed. The real soybean aliquots were composed by reproducing the emulation above. Each i^th aliquot composition exactly repeated that in the emulated i^thaliquot, where real seeds of A2704-12, A5547-127, GTS 40-3-2 soybean lines, and non-GM soybeans were used instead of red, blue and black balls. Thus, for example, in case of the aliquot with 3 seeds of line GTS 40-3-2 it contained 300 mg of the flour from GTS 40-3-2 batch+14700 mg of the flour from non-GM soybean. Weighing was done with 1% accuracy to emulate live situation.

Each aliquot containing 15 g of fine soya flour was thoroughly mixed. Since the aliquot weight was ~15 g and the sample for DNA extraction was 50 mg, there was a need to provide the best representation of recombinant DNA in the specimen, especially for the aliquots with low target seeds presence. We have therefore prepared the most possible diluted sample consisting of 100 mg of GTS 40-3-2 flour and 14900 non-GM flour, mixed thoroughly and performed 30 extractions, thus having total DNA of the aliquot divided into equal parts. C_t and standard deviation for the 30 specimens were obtained. Then we combined the single specimens into twos, threes, fours, fives, etc. (not less than 12 random combinations in each case) and found that C_t and standard deviation values stopped changing with the number of combined single specimens over four. Thus, we used seven single extraction procedures for all of aliquots, combining the resulting single extracts of genomic DNA to provide best confidence in its correct presence in the specimen used for real-time PCR.

Slope (A) estimation (self-reference calibration)

Calibration line C_t vs log [C, %] providing the slope (A) value was built using DNA extracted from the aliquot with the highest target seeds content, i.e., the one showing the lowest C_t value. Concentration of GM soybean in this aliquot was taken for 100%. DNA of the specimen in this aliquot was then diluted with DNA of non-GM soybean to obtain points with 56.2%, 31.6%, 17,8% and 10% relative concentration of the initial concentration (just to have even distribution of points along log [C] axis). Obtained DNA solutions were used as standards for building the calibration line C_t vs log [C,%]. C_t was derived in five repeats for each calibration point.

Raw data on Ct, standard deviation and self-reference calibration, calculated and actual values are given in Table 1S.

A2704-12

Results for real-time PCR performance on A2704-12 are given in Figure 5 (in blue) and Table 1S.

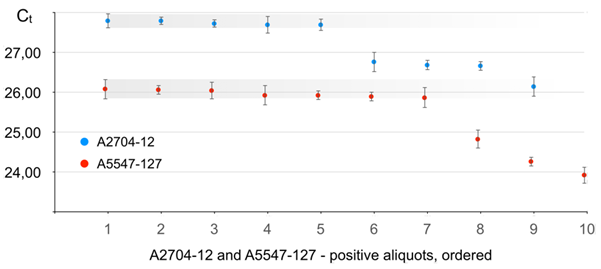
Figure 5 Real-time PCR performance on soybean lines A2704-12 and A5547-127 in the seed lot of 3000 seeds distributed in 20 aliquots. Positive aliquots arranged in the order from the lowest target seed content (latest C_t) to the highest (earliest C_t). Error bars give standard deviation values (σ) resulting from multiple repeats of testing of each aliquot (Table 1S).

Correspondence between the actual and sorted order of the aliquots can be found in Table 1S.

It is clearly seen from Figure 5 that nine aliquots showed positive for A2704-12. According to data from Figure 2 this means that total number (N) of A2704-12 beans in the 3000 lot is within 9–19 range and algorithm a) shall be applied–the aliquot with the least target seed content has exactly one target seed. It can be seen from Figure 5 that there are five aliquots (## 1 to 5), that show maximum C_t value, and the average C_t for an aliquot with 1 target seed is 27,75. The slope (A) value derived from the series of dilution of aliquot #9 (earliest C_t and highest A2704-12 content, respectively) is -3.31±0,19. The self-reference calibration line was true linear (𝝌² = 0,0651 and R² = 0.9906).

Applying these figures to the formula for n calculation, we have the following:

${\text{n}}_{\text{i}}=\frac{{\displaystyle 1}}{{\displaystyle {10}^{- \left(\frac{{\displaystyle 27.75-{\text{C}}_{\text{t}}\left(\text{i}\right)}}{{\displaystyle 3.31}}\right)}}}$

n_i is then rounded to the nearest integer value, so we get the distribution (in the order of sorted aliquots) 1,1,1,1,1,2,2,2,3, which gives N=14. And this is the exact match with the actual distribution in the seed lot, both for each aliquot and for the total presence of A2704-12.

Since A has standard deviation ${\sigma }_A=0,19$ we can calculate $n_{min}(-A=-3,31–{\sigma }_A)$ and $n_{max}(A=-3,31+{\sigma }_A)$ for each aliquot (in this particular case n values shall not be rounded). The normalized absolute deviation ∆_i for each n_i will be

${△}_{\text{i}}=\frac{{\displaystyle |{\text{n}}_{\text{max}}-{\text{n}}_{\text{min}}|}}{{\displaystyle 2{\text{n}}_{\text{i}}}}$ and ≤ ${\text{σ}}_{\text{i}}=\sqrt{\frac{{\displaystyle {\sum }^{\text{}}{△}_{\text{i}}^2}}{\text{K}-1}}$

where ${\sigma }_n$ is the normalized standard deviation and K is the number of positive aliquots.

Standard deviation for the total number of target seed in the aliquot is then${\sigma }_N={\sigma }_{n}K=0.33$ and $N=14\pm 0.33;N_{actual}=14$

SeedCalc gives $5\le N\le 23$, Confidence Interval (CI)=95% with the optimum at N=12.

A5547-127

Results for real-time PCR performance on A5547-127 are given in Figure 5 (in red) and Table 1S.

Correspondence between the actual and sorted order of the aliquots can be found in Table 1S.

As it follows from Figure 5, ten aliquots showed positive for A5547-127. According to data from Figure 2 this means that total number (N) of A5547-127 beans in the 3000 lot is within 10–22 range and algorithm a) shall be applied–the aliquot with the least target seed content has exactly one target seed. It can be seen from Figure 5 that there are seven aliquots (## 1 to 7), that show maximum C_t value, and the average C_t for an aliquot with 1 target seed is 26,09. The slope (A) value derived from the series of dilution of aliquot #10 (earliest C_t and highest A5547-127 content, respectively) is -3.50±0,16. The self-reference calibration revealed true linear regression ($\chi 2=0,0409$ and $R^2=0.9947$).

Applying the same formulas as used in A2704-12 case, we have the distribution of A5547-127 (beans through the ordered aliquots) 1,1,1,1,1,1,1,2,3,4 and the total A5547-127 content in the 3000 seed lot N=16. Again, this is the exact match with the actual distribution in the seed lot, both for each aliquot and for the total presence of the target seeds.

$n_{max}and{n}_{min}$ calculated for each aliquot with A = (-3,50–0.16) and A = (-3,50+0.16), respectively, provide ${\sigma }_N=0.59$ and the final result is:

$N=16\pm 0.59;N_{actual}=16$

SeedCalc gives 6≤N≤26, Confidence Interval (CI)=95% with the optimum at N=14.

Analysis without self-reference calibration

It can be seen from Figure 3 (P_II(N)) that for both A2407-12 and A5547-127 the criterion is applicable of having exactly one and exactly two target seeds in the aliquots with lowest and second lowest presence of target seeds. In this case all the calculations can be done without self-reference calibration because the slope (A) is derived directly from C_t values for the aliquots with one and two target seeds. Thus, $A=-(C_t\left(1\right)-C_t\left(2\right))/log2$, where C_t(1) and C_t(2) are threshold cycles for the aliquots with 1 and 2 target seeds.

It follows from Figure 5 that there are five aliquots with one target seed and three aliquots with two target seeds in case of A2704-12. For A5547-127 it is 7 and 1, respectively. Thus, we have A = -3.44 ± 0.22 (average of 15) for A2704-12 and A = -3.81 ± 0.30 for A5547-127 (average of 7). The average C_t(1) are 27.75 and 25.98, respectively. The calculations with the formulas used above give N = 14 ± 0.51 (A2704-12) and N =15 ± 0.72 (A5547-127).

This approach, not employing calibration, though convenient and applicable for the wide range of positive aliquots (9–16), is less accurate because the slope is defined by two points only in the most dilute area of target seeds content. This approach should be implied only in case when there are not less than three $C_t\left(1\right)and{C}_t\left(2\right)$ aliquots each.

GTS 40-3-2

Results for real-time PCR performance on GTS 40-3-2 are given in Figure 6 and Table 1S.

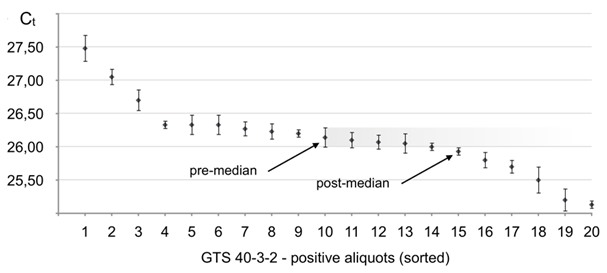
Figure 6 Real-time PCR performance on soybean line GTS 40-3-2 in the seed lot of 3000 seeds distributed in 20 aliquots. Positive aliquots arranged in the order from the lowest target seed content (latest C_t) to the highest (earliest C_t). Error bars give standard deviation values (σ) resulting from multiple repeats of testing of each aliquot (Table 1S).

Correspondence between the actual and sorted order of the aliquots can be found in Table 1S.

As it follows from Figure 6, all twenty aliquots showed positive for GTS 40-3-2, which means that the total number (N) of GTS 40-3-2 beans in the lot of 3000 seeds can be within 35–3000 range, thus, algorithm c) shall be applied, when the pre-median aliquot and the next differing aliquot above median differ by one target seed. #10  is the pre-median aliquot by definition.  It can be seen that aliquots ##7–14 show C_t within the error of the pre-median aliquot, thus, shall be considered having equal target seeds content. Then, the average C_t for the pre-median aliquot is 26.14. #15 is the first after the median, which has Ct value that differs from #10 outside the error. Self-reference calibration through dilutions of aliquot #20 showed true linearity $({\chi }^2=0.0333and{R}^2=0.9955)$ and the slope (A) was -3.44±0.13

Therefore

${\text{n}}_1=\frac{{\displaystyle 1}}{{\displaystyle \frac{{\displaystyle 1}}{{\displaystyle {10}^{\left(\frac{{\displaystyle 26.13-25,93}}{{\displaystyle -3.44}}\right)}}}-1}}$

and the number of target seeds (GTS 40-3-2 beans) in the pre-median aliquot is n1≈6.98=7.

Then n_i and N were calculated with the same formulas as for A2704-12 and A5547-127. The distribution of GTS 40-3-2 seeds is given in Figure 7.

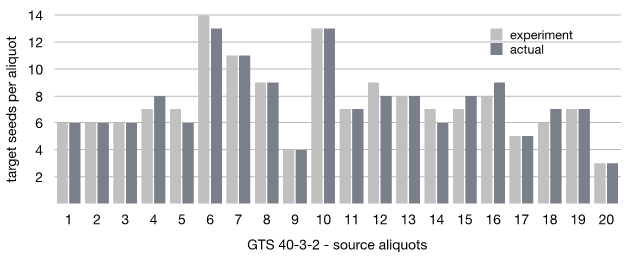
Figure 7 Experimentally estimated vs actual distribution of GTS 40-3-2 seeds in the 20 aliquots in the seed lot of 3000 seeds.

The total presence of GTS 40-3-2 in the lot of 3000 seeds was

$N=150\pm 0.54;N_{actual}=150$

SeedCalc gives 35 ≤ N ≤ «Error».

Application of the b) criteria of the common algorithm (two aliquots with the lowest target seeds content differ by exactly one target seed) gives close result.

There are some minor deviations between the actual and experimentally estimated distribution of GTS 40-3-2 across the aliquots as it can be seen from Figure 7. Thus, twelve aliquots show the exact match, four aliquots show +1 seed for the actual distribution and four show -1. The total number of the target seeds is the same in both cases though, which means that the deviations are not system error and can be explained by normal experimental and measuring errors. 

The experiment provided practical rationale for setting 150 target seeds as the upper limit of in terms of using real-time PCR. Indeed, log [n / n+1], which determines the difference between two Ct values tends to zero very quickly with increasing n. Thus, the applicability of the approach is determined by the condition

$\frac{{\displaystyle {\text{C}}_{\text{t}}\left(\text{n}\right)-{\text{C}}_{\text{t}}(\text{n}+1)}}{{\displaystyle \text{A}}}\ge \text{ log }\left(\frac{{\displaystyle \text{n}}}{{\displaystyle \text{n}+1}}\right)$

Our direct calculations checked with Monte Carlo method show that pre-median number varies within the range 2–8 when all 20 aliquots show positive (the number of target seeds in the seed lot of 3000 seeds). In case of 150 target seeds per lot of 3000 seeds probability of occurrence of the particular number of target seeds in the pre-median aliquot reveals a very sharp optimum. It is 0.0098 for 5 target seeds, 0.4461 for 6, 0.5115 for 7, and 0.0126 for 8. Probability of having less than 5 and more than 8 target seeds in the pre-median aliquot is vanishingly low. Thus, with the slope (A) value being between -3.0 and -3.5 (most often observed in the experiments) the practical detection limit condition is

$C_t\left(m^{-}\right)–C_t\left(m^{+}\right)\ge 0.17-0.20$

where m^- and m⁺ is the number of target seeds in the identified pre-median and post-median aliquots, respectively. This condition is very close to the experimental and measurement errors. These considerations give us another surprising, though quite expected result–accuracy and reliability of the method grows along with decreasing target seeds content. Indeed, the difference between threshold cycles for aliquots containing n and (n+1) target seeds is much more visible with lower n, and it is easier to precisely differentiate between them.

The proposed approach works correctly (with the confidence > 95%) on discreet systems within concentration range 0.033–5% and can be used without any reference (self-reference calibration) within the wide range of target seed content (0.3-2%). Since the approach employs seed count mode, it does not depend upon weight difference between bulk and target seeds and eliminates the ambiguity that can arise due to the possible difference in the efficiency of DNA extraction from the target seeds and the certified reference material, as well as the difference in PCR performance. The approach appears to have high potential if combined with digital PCR, when a specific number of copies of the target DNA is assigned to exactly one seed, thus the positive aliquots series becomes plain arithmetic progression, requiring no calibration at all. The lower limit of quantitation can be easily decreased by increasing the size of the initial seed lot and the number of aliquots. Thus, in case of 9000 seeds and 60 aliquots it will be 0.01% with ~99.97% confidence, though in many cases it turns impractical due to increasing labor and laboratory costs. Detailed analysis of the connection between detected level of adventitious presence and the costs is given elsewhere.¹¹

The proposed approach can be applied not on biotechnology seeds only, but on tracing whatever marker not appearing in the bulk seeds. Thus, we have successfully quantified the occasional presence of millet seeds in live sample of commodity rapeseeds by tracing caat (cytosolic aspartate aminotransferase) gene, with the cross-check of the results with manual seed counting.

We have also successfully experimented with weighing aliquots with the mixture of the balls, that were the same in size but differed in weight, finding the weight of each type of the balls.

And this means that the proposed approach may be applied to whatever physical method of testing, provide there is an established dependence between the observed signal and the concentration of the traced trait.

There are no conflicts to declare.

The authors express their most sincere gratitude to Mr. Konstantin Kozlovsky (“SunLineStroy” Company) for his fruitful contribution to the theoretical part of the work, and to Mr. Vitaly Smirnov (“Group of Companies SODRUGESTVO”) for providing the material.

1. Mazzara M, Paoletti C, Corbisier P, et al. Kernel Lot Distribution Assessment (KeLDA): A Comparative Study of Protein and DNA-Based Detection Methods for GMO Testing, Food Analytical Methods. 2013;6(1):210–220.
2. Bogožalec-Košir A, Demšar T, Štebih D, et al. Digital PCR as an effective tool for GMO quantification in complex matrices, Food Chemistry. 2019;294:73–78.
3. Laffont JL, Remund KM, Wright D, et al. Testing for adventitious presence of transgenic material in conventional seed or grain lots using quantitative laboratory methods: statistical procedures and their implementation, Seed Science Research. 2005;15(3):197–204.
4. Brualdi RA. Introductory Combinatorics. 5th ed, New Jersey: Pearson Prentice Hall; 2010.
5. Joarder AH. Hypergeometric Distribution and Its Application in Statistics. In: Lovric M, editor. International Encyclopedia of Statistical Science,Germany:Springer Berlin Heidelberg; 2011. p. 641–643.
6. Grinstead MC, Snell JL. Introduction to Probability. 2nd Revised ed, USA: American Mathematical Society; 1997.
7. Knuth DE. The Art of Computer Programming: Fundamental algorithms. 3rd ed, USA: Addison-Wesley Professional; 1997.
8. Mazzara M, Delobel C, Grazioli E, et al. Event-Specific Method for the Quantification of Soybean Line A2704-12 Using Real-Time PCR - Validation Report and Protocol - Soybean Seeds Sampling and DNA Extraction. Online Publication. 2007.
9. Delobel C, Bogni A, Mazzara M, et al. Event-specific Method for the Quantification of Soybean Line A5547-127 Using Real-time PCR - Validation Report and Protocol. Online Publication. 2009.
10. Mazzara M, Munaro B, Larcher S, et al. Event-specific Method for the Quantification of Soybean Line 40-3-2 Using Real-time PCR - Validation Report and Protocol - Report on the Validation of a DNA Extraction Method for Soybean Seeds, Online Publication. 2007.
11. European Network of GMO Laboratories Working Group “Seed Testing” (WG-ST) Working Group Report, Online Publication. 2015.