eISSN: 2378-315X


Research Article Volume 1 Issue 3
1Department of Statistics, Jahangirnagar University, Bangladesh
2Department of Mathematical Sciences, Ball State University, Indiana, USA
Correspondence: Munni Begum, Department of Mathematical Sciences, Ball State University, Indiana, USA, Tel 1-765-285-8673
Received: November 12, 2014 | Published: December 11, 2014
Citation: Alam M, Farazi MR, Stiglitz J, Begum M (2014) Statistical Modeling of the Number of Deaths of Children in Bangladesh. Biom Biostat Int J 1(3): 00014. DOI: 10.15406/bbij.2014.01.00014
Efforts to reduce the number of children’s death in developing countries through health care programs focus more to the prevention and control of diseases than to determining the underlying risk factors/predictors and addressing these through proper interventions. This study aims to identify socioeconomic and demographic predictors of the number of children’s death to women aged 12-49 from the Bangladesh Health and Demographic Survey (BDHS) administered in 2011. The number of children’s death in a family is a non-negative count response variable. The average number of children’s death is found to be 28 per 100 women with a variance of 44per 100 women. Thus Poisson regression model is not a proper choice to predict the mean response from the BDHS data due to the presence of over-dispersion. In order to address over-dispersion, we fit a Negative Binomial Regression (NBR), a Zero-Inflated Negative Binomial Regression (ZINBR) and a Hurdle Regression (HR) model. Among these models, ZINBR fits the data best. We identify respondent’s age, respondent’s age at 1st birth, gap between 1st birth and marriage, number of family members, region, religion, respondent’s education, husband’s education, incidence of twins, source of water, and wealth index as significant predictors for the number of children’s death in a family from the best fitted model. Identification of the risk factors of the number of children’s death is an important public health issue and should be carried out correctly for the much needed intervention.
Keywords: number of child deaths, predictors, NBR, ZINBR, HR
BDHS, bangladesh health and demographic survey; NBR, negative binomial regression; ZINBR, zero-inflated negative binomial regression; HR, hurdle regression
Reduction of child mortality is one of the prime objectives of the south eastern Asian nation Bangladesh. Bangladesh has made impressive progress in health and human development since its emergence as an independent nation in 1971.1,2 Although the country achieved significant improvement in public health and in controlling the morbidities and mortalities from preventable diseases, child mortality is still a major public health issue. Every year between 8 and 11 million children die worldwide before reaching their fifth birthday.3 The underlying cause for 60% of the deaths of children under the age five in Bangladesh is malnutrition.3,4 The primary objective of the current study is to identify socioeconomic and demographic risk factors/predictors of the number of children"s death for women aged 12-49 from the Bangladesh Health and Demographic Survey (BDHS) administered in 2011. It is useful for the policymakers to have a set of risk factors of the number of children"s death in order to develop guidelines and address these risk factors with proper intervention. Framing proper guidelines and policies to reduce child mortality will insure the sustainability of achieving the Millennium Development Goal (MDG)4 relating child mortality.
In terms of demographic and socioeconomic determinants, maternal age and education are found to be strongly correlated with child morality.1,5–11 Although the relationship between parental education and the number of children"s death is complex, a number of studies have illustrated that children of less educated parents tend to have a higher mortality rate than children of well-educated ones.6,9,10–13 Parental education, more importantly maternal education, is identified as a strong predictor of child morality.5,9–11 Other determinants of child mortality may include rural-urban residency,1,3,11,13,14 number of children in a household,1,3,14 water source1,12 and toilet facility.1,5,11,14 Most of these studies related to children"s mortality and children"s survival used proportional hazards models and multivariable logistic regression.8 For instance, Bhuiya et al.8 applied a proportional hazard models to study strong relationships with childhood mortality in Bangladesh. Majumder et al. 9 used multivariate analysis to identify socioeconomic and environmental determinants of children survival in Bangladesh. Chowdhury et al.11 used multivariate proportional hazards models to find covariates that associated with neonatal and post-neonatal mortality in Bangladesh. Some studies addressed the number of malnourished children.2–5 As no literature is available to the best of our knowledge regarding total number of children"s death among the women of age group 12-49 years in Bangladesh, we attempt to explore the nature of the number of children"s deaths and to identify associated risk factors/ covariates in this study.
A number of regression models for the count response, namely, standard Poisson Regression model, Negative Binomial Regression (NBR) model and Generalized Poisson Regression (GPR) model had been addressed in the literature.3 Applications of these models are based on the assumptions that the mean and variance of the response variable are equal under the standard Poisson model. The GPR model allows flexibility in dealing with over-dispersion or under-dispersion.3 More specifically, an NBR model is suggestive for dealing with over-dispersion.15
The main objective of the study is to develop a predictive model for the number of child deaths in families in Bangladesh. In this study we applied Negative Binomial Regression (NBR), Zero-Inflated Negative Binomial Regression (ZINBR) and Hurdle Regression (HR) to the count response, number of children"s death, to identify statistically significant predictors/risk factors.
Study participants
Women aged 12-49 from the Bangladesh Health and Demographic Survey (BDHS) administered in 2011by the National Institute of Population Research and Training (NIPORT), ICF International (USA), and Mitra and Associates. BDHS 2011 is the sixth national demographic and health survey in Bangladesh. The findings of this study can be used for evaluating the Health, Population and Nutrition Sector Development Program (HPNSDP). Sixteen trained interviewing teams administered 17,842 successful interviews of ever-married women aged 12-49. Information was collected from ever-married women of the selected households. The detailed methodology of the survey design, data collection, and data management has been described elsewhere.1 For this study, we ignore all the missing values and exclude the subjects with missing entries assuming that observations are missing completely at random. Due to some missing observations, finally, we carry out our analysis on data collected from 15,044 married women aged 12-49 years in Bangladesh. The box plot (Figure 1) for the response shows that there is an unusual observation. However, this response value has been kept in the analysis considering its plausibility.
Data management
The response variable, the number of children"s death of ever-married women surveyed, has been derived by adding up total number of son"s death and total number of daughter"s death of a mother. The predictors were assessed by questions regarding age of the respondent (categorized in age groups in years: 13-19, 20-24, 25-29, 30-34, 35-39, 40-44 and 45-49), husband age group in years (13-19, 20-24, 25-29, 30-34, 35-39, 40-44, 45-49, 50+), respondent age at 1st birth in years (13-19, 20-24, 25-29, 30-39 and 40-49), gap between marriage and 1st birth in months (0-24, 25-60, 60+), number of family members (<4, 5-7,8-10, 10+), region(seven divisions: Barisal, Chittagong, Dhaka, Khulna, Rajshahi, Rangpur, and Sylhet), place of residence (rural, urban), religion (Islam, others; where "others" includes Hinduism, Buddhism, Christian and unknown religions), respondent"s education (no education, primary school: 1-5 years education, secondary: 6-10 years education, higher: 11+ years education), husband"s education (no education, primary school: 1-5 years education, secondary: 6-10 years education, higher: 11+ years education), does respondent currently work (yes, no), currently residing (living with husband, living elsewhere), incidence of twins (yes, no), has electricity (yes, no), water source (piped, tube-well, and other), toilet facility (standard or not), wealth index was calculated in quintiles (1= poorest and 5 = wealthiest) based on household asset data and access to media (yes or no).
Model justification
Poisson regression model is a natural choice for count response variables. However, in the presence of over-dispersion, Poisson regression model does not perform well in best fitting the data and for prediction. In this study, we test over-dispersion,15,16 where the null hypothesis is that there is no over-dispersion in the data. Hence, the Poisson regression model is the null model against any other alternative model with over-dispersion. Following the notations of Deans and Lawless,15,16 we let Yi be the response from their subject with covariates Xi.. Then Yi is distributed as Poisson with mean µi = µi(Xi; β), where β is ap-dimensional vector of unknown coefficients. We denote the possible extra-Poisson variation byv
i+ τ µi2and the null hypothesis for testing over-dispersion becomes, H0: τ = 0. Failure to reject the null hypothesis leads to the Poisson regression model. In this study we perform, Dean"s PB15 test for over-dispersion using a R packaged DCluster18,19 that generates the test statistic PB = 13.5292 with p-value <0.000. Rejection of H0 leads to the application of Negative Binomial type models. Since the variance is greater than the mean and there is about 79% zero counts for the response variable, we apply Zero-Inflated Negative Binomial Regression (ZINBR) and Hurdle Regression (HR) models along with the Negative Binomial Regression (NBR) model to analyze the data.
Data analysis
Simple summary statistics (frequency and percentages) are calculated for the selected socioeconomic and demographic risk factors. Sample mean and sample variance of the response variable are calculated to have an idea of its distribution pattern. Bivariate analysis (based on Pearson Chi-square test) has been performed to examine the association between response variable and each of the selected predictors. To validate the Chi-square test, we categorize the response variable as 0 deaths, 1-2 deaths, and ≥3 deaths. Otherwise the sell frequencies become <5 or zero violating the asymptotic Chi-square assumption. All the significant predictors are then included in the NBR, ZINBR and HR models. For HR model we exclude the predictor age at 1st birth since inclusion of the variable in the model makes the Hat matrix (X(X/X)-1>X/) singular. NBR model is better suited to the count response; number of deaths of children to women aged 12-49, due to the presence of over-dispersion. In the case of excessive number of zeros ZINBR and HR perform well in terms modeling number of children"s death. We applied these three models for estimating regression parameters (β) including p-values based on Wald statistics. Finally, we calculated incidence rate ratio (IRR) for all groups of categorical variables. The statistical software package R (Studio) is used for extracting information from BDHS 2011, recoding and model fitting including parameter estimation of the models. We compared the results from NBR, ZINBR and HR models and goodness of fit statistic Akike Information Criteria (AIC).
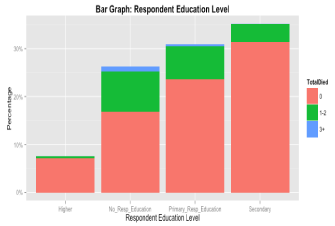
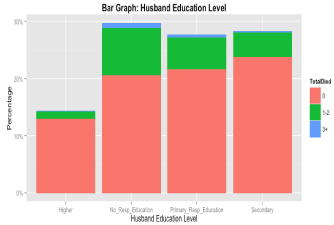
The average age of the surveyed women was 31.44 years while the average age of the husband was 40.97 years. The average age of the women at their first experience of childbirth was 17.89 years. On average a woman gave 2.85 births in their lifetime and the average family size is 5.6.Women gave birth to their first child approximately 3 years after their marriage. About 21% of the women experienced child death and 1.3% women experienced three or more child deaths. 17.47% of women are from the lowest wealth index category and 23.37% are from the highest wealth category. About twenty-six percent of the women had no education. Few of them (7.5%) had 11+ year of education. On the other hand, 29% of the husbands were illiterate but 14% had at least11+ year of education. The majority of the women were Muslims (88.71%). About 66% of the respondents were from urban area. In case of family water sources, 80.52% of families depend on tube-well. About 57% of the families use standard toilets. The percentage of women reported that they had no access to any kind of media is 35%.Box plot (Figure 1) for the number of deaths in a family depicts only one unusual observation. It reveals that one mother experienced 15 child deaths. Figure 2 shows that the distribution of number of children"s death in a family is highly positively skewed. Incidence of more than three child death is almost negligible. Scatter plot in (Figure 3) shows that number of child deaths increases as the respondent"s age increases. The distribution of the number of children"s death with respect to mother"s education (Figure 4) postulates the high incidence of child death for the mothers having no education. Figure 5 also indicates that families with no education of the household head experience more child death. Proportion of deaths for male children and female children are 0.53 and 0.47 respectively. However, the difference of the proportion is not statistically significant (p-value=0. 54).
Simple association: Response versus predictor
The associations between the response variable and each of risk factors considered have been examined with Pearson Chi-square at 5% significance level (Table 1) with the following hypothesis H0i: There is no association between the number of children"s death and their risk factor. Table 2 shows that all the risk factors except respondent"s current work status are significantly associated with the number of deaths of children.
Model fitting
We compare the fitted models with respect to AIC. Although NBR and ZINBR produce very close results, we see ZINBR model acquires the lowest AIC (17,690) among the three fitted models (Table 3). Accordingly, we assert that ZINBR is the best predictive model for the number of deaths of children of women aged 12-49 in Bangladesh and present results from this model. According to the results of ZINBR model (Table 4), one or more of the categories of the predictors (respondent"s age, respondent"s age at 1st birth, gap between 1st birth and marriage, number of family members, region, religion, respondent"s education, husband"s education, incidence of twins, source of water, wealth index)are statistically significantly associated with the number of children"s death in a family. The NBR model also suggests almost similar findings [results not shown].On the other hand, HR model[results not shown] shows gap between 1st birth and marriage, number of household members, region, religion, incidence of twins, and toilet type are significantly related with the response variable. The ZINBR model (Table 4) shows that as the age of mothers increase, they experience higher rate of incidence of child death during their childbearing ages. Mothers having first birth between 20 to 24year"s experiences 35.90% lower child death incidence than the mothers having first birth between 13 to19 years.
|
Frequency |
Cumulative Frequency |
Percentage |
Cumulative Percentage |
Total Children Died |
||||
<2 |
11880 |
11880 |
78.97 |
78.97 |
03-May |
2923 |
14803 |
19.43 |
98.4 |
6+ |
241 |
15044 |
1.6 |
100 |
Age of Respondent |
||||
13-19 |
1018 |
1018 |
6.77 |
6.77 |
20-24 |
2899 |
3917 |
19.27 |
26.04 |
25-29 |
3122 |
7039 |
20.75 |
46.79 |
30-34 |
2505 |
9544 |
16.65 |
63.44 |
35-39 |
2104 |
11648 |
13.99 |
77.43 |
40-44 |
1907 |
13555 |
12.68 |
90.1 |
45-49 |
1489 |
15044 |
9.9 |
100 |
Husband Age |
||||
15-19 |
16 |
16 |
0.11 |
0.11 |
20-24 |
477 |
493 |
3.17 |
3.28 |
25-29 |
1710 |
2203 |
11.37 |
14.64 |
30-34 |
2314 |
4517 |
15.38 |
30.03 |
35-39 |
2543 |
7060 |
16.9 |
46.93 |
40-44 |
2256 |
9316 |
15 |
61.93 |
45-49 |
2073 |
11389 |
13.78 |
75.7 |
50+ |
3655 |
15044 |
24.3 |
100 |
Age at 1st Birth |
||||
13-19 |
11343 |
11343 |
75.4 |
75.4 |
20-24 |
3024 |
14367 |
20.1 |
95.5 |
25-29 |
556 |
14923 |
3.7 |
99.2 |
30-39 |
119 |
15042 |
0.79 |
99.99 |
40-49 |
2 |
15044 |
0.01 |
100 |
Frequency |
Cumulative Frequency |
Percentage |
Cumulative Percentage |
|
Gap Between Marriage and 1st Birth |
||||
<24 Months |
8360 |
8360 |
55.57 |
55.57 |
25-60 Months |
5238 |
13598 |
34.82 |
90.39 |
60+ Months |
1446 |
15044 |
9.61 |
100 |
Household Members |
||||
< 4 |
5729 |
5729 |
38.08 |
38.08 |
05-Jul |
751 |
6480 |
4.99 |
43.07 |
08-Oct |
6732 |
13212 |
44.75 |
87.82 |
8+ |
1832 |
15044 |
12.18 |
100 |
Region |
||||
Barisal |
1768 |
1768 |
11.75 |
11.75 |
Chittagong |
2440 |
4208 |
16.22 |
27.97 |
Dhaka |
2533 |
6741 |
16.84 |
44.81 |
Khulna |
2225 |
8966 |
14.79 |
59.6 |
Rajshahi |
2236 |
11202 |
14.86 |
74.46 |
Rangpur |
2122 |
13324 |
14.11 |
88.57 |
Sylhet |
1720 |
15044 |
11.43 |
100 |
Residence |
||||
Rural |
5153 |
5153 |
34.25 |
34.25 |
Urban |
9891 |
15044 |
65.75 |
100 |
Religion |
||||
Islam |
13345 |
13345 |
88.71 |
88.71 |
Other |
1699 |
15044 |
11.29 |
100 |
Respondent's Education |
||||
No Education |
1138 |
1138 |
7.56 |
7.56 |
Primary |
3960 |
5098 |
26.32 |
33.89 |
Secondary |
4656 |
9754 |
30.95 |
64.84 |
Higher |
5290 |
15044 |
35.16 |
100 |
Frequency |
Cumulative Frequency |
Percentage |
Cumulative Percentage |
|
Husband Education |
||||
No Education |
2157 |
2157 |
14.34 |
14.34 |
Primary |
4474 |
6631 |
29.74 |
44.08 |
Secondary |
4159 |
10790 |
27.65 |
71.72 |
Higher |
4254 |
15044 |
28.28 |
100 |
Is Respondent Currently working? |
||||
No |
13264 |
13264 |
88.17 |
88.17 |
Yes |
1780 |
15044 |
11.83 |
100 |
Husband’s Working Status |
||||
Businessman |
3645 |
3645 |
24.23 |
24.23 |
Labor Intensive |
10292 |
13937 |
68.41 |
92.64 |
Service/Professional |
1107 |
15044 |
7.36 |
100 |
Respondent Currently Residing with |
||||
Living Elsewhere |
1646 |
1646 |
10.94 |
10.94 |
Living with Husband |
13398 |
15044 |
89.06 |
100 |
Have any Twin |
||||
No |
14686 |
14686 |
97.62 |
97.62 |
Yes |
358 |
15044 |
2.38 |
100 |
Electricity |
||||
No |
6097 |
6097 |
40.53 |
40.53 |
Yes |
8947 |
15044 |
59.47 |
100 |
Water Source |
||||
Others |
1323 |
1323 |
8.79 |
8.79 |
Piped Water |
1607 |
2930 |
10.68 |
19.48 |
Tube-well Water |
12114 |
15044 |
80.52 |
100 |
Type of Toilet |
||||
Not Standard |
6488 |
6488 |
43.13 |
43.13 |
Standard |
8556 |
15044 |
56.87 |
100 |
Frequency |
Cumulative Frequency |
Percentage |
Cumulative Percentage |
|
Wealth Index |
||||
Lowest |
2628 |
2628 |
17.47 |
17.47 |
Second |
2826 |
5454 |
18.78 |
36.25 |
Third |
2918 |
8372 |
19.4 |
55.65 |
Fourth |
3156 |
11528 |
20.98 |
76.63 |
Highest |
3516 |
15044 |
23.37 |
100 |
Media Access |
||||
Access |
9837 |
9837 |
65.39 |
65.39 |
No Access |
5207 |
15044 |
34.61 |
100 |
Table 1 Prevalence of the number of child deaths with predictors, BDHS, 2011
Chi Square |
df |
p-value |
|
Respondent Age |
1524.181 |
12 |
0.00000 |
Husband Age |
1282.327 |
14 |
0.00000 |
Respondent Age at 1st Birth |
111.307 |
8 |
0.00000 |
Gap between Marriage and 1st Birth |
14.24685 |
4 |
0.00655 |
Number of Members in the Family |
19.21245 |
6 |
0.00382 |
Region |
65.18007 |
12 |
0.00000 |
Residence |
67.39046 |
2 |
0.00000 |
Religion |
18.33311 |
2 |
0.00010 |
Respondent Education |
1117.853 |
6 |
0.00000 |
Husband Education |
526.0294 |
6 |
0.00000 |
Is Respondent Currently Working |
1.158246 |
2 |
0.56039 |
Husband Occupation |
66.90243 |
4 |
0.00000 |
With Whom Respondent Currently Living |
43.05137 |
2 |
0.00000 |
Any Incidence of Twins in the Family |
564.2712 |
2 |
0.00000 |
Having Electricity |
121.0506 |
2 |
0.00000 |
Source of Water |
78.77498 |
4 |
0.00000 |
Type of Toilet |
68.68566 |
2 |
0.00000 |
Wealth Index |
283.5333 |
8 |
0.00000 |
Access to Media |
314.0064 |
2 |
0.00000 |
Table 2 The association between number of child deaths and predictors, BDHS, 2011
AIC |
Log-Likelihood |
|
NBR |
17756.00 |
-8825.992 |
ZINBR |
17690.00 |
-8826 |
Hurdle |
20118.00 |
-10040.00 |
Table 3 Model Comparison
Coeff |
SE |
Wald |
P-Val |
RR |
||
(Intercept) |
-3.040 |
1.028 |
-2.957 |
0.003 |
0.048 |
|
Respondent Age (Year) |
||||||
20-24 |
0.375 |
0.145 |
2.584 |
0.010 |
1.455 |
|
25-29 |
0.743 |
0.154 |
4.835 |
0.000 |
2.103 |
|
30-34 |
1.264 |
0.161 |
7.844 |
0.000 |
3.539 |
|
35-39 |
1.470 |
0.166 |
8.857 |
0.000 |
4.349 |
|
40-44 |
1.845 |
0.169 |
10.951 |
0.000 |
6.330 |
|
45-49 |
2.152 |
0.171 |
12.598 |
0.000 |
8.599 |
|
Husband Age (Year) |
||||||
20-24 |
0.052 |
1.027 |
0.050 |
0.960 |
1.053 |
|
25-29 |
-0.052 |
1.021 |
-0.050 |
0.960 |
0.950 |
|
30-34 |
0.076 |
1.022 |
0.075 |
0.940 |
1.079 |
|
35-39 |
0.058 |
1.023 |
0.057 |
0.954 |
1.060 |
|
40-44 |
-0.041 |
1.024 |
-0.040 |
0.968 |
0.960 |
|
45-49 |
0.060 |
1.024 |
0.059 |
0.953 |
1.062 |
|
50+ |
0.174 |
1.025 |
0.170 |
0.865 |
1.190 |
|
Respondent Age at 1st Birth (Year) |
||||||
20-24 |
-0.444 |
0.053 |
-8.421 |
0.000 |
0.641 |
|
25-29 |
-0.633 |
0.116 |
-5.458 |
0.000 |
0.531 |
|
30-39 |
-1.155 |
0.283 |
-4.080 |
0.000 |
0.315 |
|
40-49 |
-10.946 |
201.965 |
-0.054 |
0.957 |
0.000 |
|
The time interval between marriage and 1st month(Birth) |
||||||
25-60 |
-0.149 |
0.037 |
-3.986 |
0.000 |
0.862 |
|
60+ |
-0.035 |
0.063 |
-0.547 |
0.584 |
0.966 |
|
Number of Members in the Family |
|
|||||
5-7 |
-0.095 |
0.038 |
-2.506 |
0.012 |
0.910 |
|
8-10 |
-0.266 |
0.059 |
-4.484 |
0.000 |
0.766 |
|
10+ |
-0.126 |
0.089 |
-1.411 |
0.158 |
0.881 |
|
|
Coeff |
SE |
Wald |
P-Val |
RR |
|
Region (Division) |
|
|||||
Chittagong |
0.066 |
0.064 |
1.035 |
0.301 |
1.069 |
|
Dhaka |
-0.061 |
0.065 |
-0.940 |
0.347 |
0.941 |
|
Khulna |
-0.397 |
0.068 |
-5.821 |
0.000 |
0.672 |
|
Rajshahi |
-0.232 |
0.066 |
-3.488 |
0.000 |
0.793 |
|
Rangpur |
-0.194 |
0.066 |
-2.920 |
0.003 |
0.824 |
|
Sylhet |
0.264 |
0.067 |
3.921 |
0.000 |
1.303 |
|
Residence |
||||||
Urban |
-0.016 |
0.044 |
-0.359 |
0.719 |
0.984 |
|
Religion |
||||||
Others |
-0.226 |
0.060 |
-3.798 |
0.000 |
0.798 |
|
Respondent educational status |
||||||
No Education |
0.723 |
0.146 |
4.952 |
0.000 |
2.060 |
|
Primary |
0.596 |
0.143 |
4.176 |
0.000 |
1.814 |
|
Secondary |
0.228 |
0.137 |
1.661 |
0.097 |
1.256 |
|
Husband Educational Status |
|
|||||
No Education |
0.452 |
0.098 |
4.607 |
0.000 |
1.572 |
|
Primary |
0.383 |
0.096 |
4.003 |
0.000 |
1.466 |
|
Secondary |
0.251 |
0.091 |
2.745 |
0.006 |
1.285 |
|
Is Respondent Currently Working |
||||||
Yes |
0.006 |
0.054 |
0.119 |
0.906 |
1.006 |
|
| Husband Occupational Status | ||||||
| Labor | -0.075 | 0.042 | -1.779 | 0.075 | 0.928 | |
| Professional | 0.046 | 0.097 | 0.475 | 0.634 | 1.047 | |
| Respondent Currently Living with | ||||||
| Husband | 0.116 | 0.065 | 1.788 | 0.074 | 1.123 | |
| Incidence of Twin | ||||||
| Yes | 1.263 | 0.064 | 19.604 | 0 | 3.536 | |
| Having Electricity | ||||||
| Yes | -0.083 | 0.049 | -1.703 | 0.089 | 0.921 | |
| Source of Water | ||||||
| Piped water | -0.192 | 0.101 | -1.907 | 0.056 | 0.825 | |
| Tube-well | -0.096 | 0.071 | -1.356 | 0.175 | 0.908 | |
| Toilet Type | ||||||
| Standard | -0.067 | 0.039 | -1.721 | 0.085 | 0.935 | |
| Wealth Index | ||||||
| Poorest | 0.008 | 0.051 | 0.156 | 0.876 | 1.008 | |
| 3rd Group | -0.074 | 0.055 | -1.342 | 0.18 | 0.929 | |
| 4th Group | -0.13 | 0.064 | -2.039 | 0.041 | 0.878 | |
| Wealthiest | -0.323 | 0.081 | -3.971 | 0 | 0.724 | |
| Access to Media | ||||||
| No | 0.057 | 0.041 | 1.406 | 0.16 | 1.059 | |
Table 4 Results of multivariate Zero-Inflated Negative Binomial (ZINBR) and Negative Binomial regression (NBR) and Hurdle Model (HR) to study the total number of deaths of children in Bangladesh
None.
Authors declare that there are no conflicts of interests.

©2014 Alam, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.
2 7