eISSN: 2378-315X


Research Article Volume 3 Issue 1
1Department of Statistics, Wachemo University, Ethiopia
2Department of Epidemiology and Biostatistics, Jimma University, Ethiopia
3Department of Statistics, Jimma University, Ethiopia
Correspondence: Getachew Tekle, Wachemo University, Faculty of Natural &computational Sciences, department of Statistics, Hossana, Ethiopia
Received: December 08, 2015 | Published: January 9, 2016
Citation: Tekle G. Statistical analysis of cd4+ cell counts progression of hiv-1-positive patients enrolled in antiretroviral therapy at hossana district queen elleni mohamad memorial hospital, south ethiopia. Biom Biostat Int J. 2016;3(1):17-25. DOI: 10.15406/bbij.2016.03.00057
Background: Human immunodeficiency virus/acquired immune deficiency syndrome (HIV/AIDS) have caused the world most shocking tragedy and risk. Mortality among patients on HAART is associated with high baseline levels of HIV RNA, WHO stage III or IV at the beginning of treatment, low body mass index, severe anemia, low CD4+ cell count, type of ART treatment, gender, resource-poor settings, and poor adherence to HAART.
Objective: The main objective of this study was to make use of appropriate modeling approach to CD4+ cell progression and identify the potential risk factors affecting the CD4+ cell progression of ART patients in Hossana District Queen Elleni Mohamad Memorial Hospital.
Methods: In this longitudinal retrospective based study secondary data was used from Hossana District Queen Elleni Mohamad Memorial Hospital. The study population consists of 222 HIV-1-positive patients, measured repeatedly at least one time on each patient who are 15 years old or older those treated with ART drugs from September 2011 to May 2014. The data was analyzed using SAS 9.2 version procedure NLMIXED. Poisson, Poisson-gamma, Poisson-normal, and Poisson-normal-gamma models were applied to study over-dispersion and correlation in the data.
Results: A total of 222 adult ART HIV-1-positive patients were included in this study. Out of these ART patients, 131(59%) were female patients and 91(41%) were male patients; 65(29.30%) were followed the drug combinations properly; the mean and standard deviation of baseline CD4+ cell counts were 355.9 and 321.4 cells per milliliter of blood, respectively; the mean and standard deviation of age of patients (p=0.0001) were 31.06 and 8.50 years, respectively; patients were followed for a mean of 24 months (p=0.0001). The analysis showed that the covariates significant for the progression of CD4+ cell counts were age of the patient, time since seroconversion, and sex at 5% level of significance.
Conclusion: On average CD4+ cell count increases after patients initiated to the HAART program (the disease rate declines). The progression of end outcome depends on patient’s baseline socio-demographic characteristics. For the presence of over-dispersion, and clustering, the Poisson-normal-gamma model results in improvement in model fit.
Keywords: CD4+ cell count; Poisson-normal-gamma model; Over dispersion; Correlation
Background
Human immunodeficiency virus/acquired immune deficiency syndrome (HIV/AIDS) have caused the world most distressing tragedy and danger. More than 25 million people worldwide have died of AIDS since 1981, as reported by Avert Org.1 In 2005 Ethiopia launched free ART, over 71, 000 were initiated by the end of November 2006. 241 hospitals and health centers are now providing HIV care and treatment services in regions of the country.
According to Bayeh et al.,2 enumeration of CD4+ T cell count has been useful to initiate and monitor therapy in HIV infected individuals taking potent ART.
Count data are collected repeatedly over time in many applications, such as biology, epidemiology, and public health. Such data are often characterized by the following features: correlation due to the repeated measures is usually accounted for using subject-specific random effects, which are assumed to be normally distributed. The sample variance may exceed the mean, over-dispersion. Hence, appropriate modeling approaches which can overcome these issues and which lighten data analysis are needed.
Statement of the problem
The CD4+ cell count still remains the major determinant or measure of the cell mediated immunity. Currently, there is no enough evidence showing that all the ART centers in Ethiopia have implemented research tools to monitor patient’s immune (CD4) response to HAART within a specified time frame and identification of factors that might be associated with the poor CD4-Lymphocyte response to HAART.
Hence, this study seeks to answer the following questions:
Objectives of the study
General objective: To make use of appropriate modeling approach to CD4+ cell counts progression and identify the potential risk factors affecting the CD4+ cell progression of ART patients in Hossana District Queen Elleni Mohamad Memorial Hospital.
Specific objectives
Significance of the study
This study will have the following benefits:
Source of data and sample size
The data was obtained from Hossana Queen Elleni Mohamad Memorial Hospital, SNNPR, Ethiopia from September, 2011 to May, 2014. The hospital is found in Hosanna town which is 235 km away from Addis Ababa. Persons living with HIV/AIDS, age greater than or equal to 15 years and started ART treatment in Hossana Queen Elleni Mohamad Memorial Hospital were included in the study. Individuals of 222 HIV patients in the HAART with a minimum of one and maximum of nineteen measures were selected. A retrospective longitudinal study design was conducted. Data was analyzed by SAS version 9.2 using NLMIXED procedure.
Study variables
Dependent/response variable
Enumeration of CD4+ cell counts (CD4+ T cells) per mm3 of blood of ART patients, which is count.
Independent/explanatory variables
Eleven covariates were used to meet the goal of the study. These are:
Baseline age, Time since a month of seroconversion, Sex of the patient, Level of Education, (WHO) Clinical Stage, Area/residence of the patient, Adherence to any of the drugs, Employment status, Religion, and Marital Status.
Method of data analysis
Explanatory data analysis:
Statistical models
Generalized linear model/poisson model
Generalized linear models are usually in use for modeling univariate non-Gaussian data.
The Poisson distribution belongs to the exponential family and is commonly used for the analysis of count data.
The distribution of outcome is Y ~ Poisson , thus:
(1)
The Poisson regression model, with a vector of p fixed, but unknown regression coefficients is given by
Over-dispersion model
For count data, we consider the assumption that the variance proportional to the mean (in Poisson distribution). Specifically,
Where, is over dispersion parameter if , then the variance equals the mean and we obtain the Poisson mean-variance relationship. When the mean and variance are not equal (over-dispersion), often the Poisson distribution replaced with Negative Binomial Distribution.
Start from a Poisson regression model and add a multiplicative random effect to represent unobserved heterogeneity.
(2)
has a gamma distribution with parameters and unconditional distribution of the outcome, which happens to be the negative binomial distribution.
Generalized linear mixed model
According to Engel & Keen,3 Molenberghs & Verbeke,4 and Pinheiro & Bates,5 when non-Gaussian data are repeatedly measured like CD4+ cell counts, the GLM is usually extended to GLMMs, with a subject-specific random effect, usually a Gaussian type, added in the linear predictor to capture the correlation.
GLMMs combine the properties of linear mixed models and generalized linear models.
(3)
<
Where, : The mean of which is related to the covariates of X by link function
: Covariates of the ith patient for the jth time
: Regression coefficients of
: The covariates of the random effects of the ith patient at jth time
Poisson-normal-gamma model
Correlation and over-dispersion can crop up simultaneously, in practice. Combining ideas from the over dispersion and the GLMM the Poisson model with normal and gamma random effects can be specified as:
(4)
with [6], where be the jth outcome measured for subject and p-dimensional and q dimensional vectors of known covariate values, and a p-dimensional vector of unknown fixed regression coefficients.
Model comparison/selection and variable selection
NLMIXED procedure fits nonlinear mixed models by maximizing an approximation to the likelihood integrated over the random effects.
It uses adaptive Gaussian quadrature method (MLH) by default.
Although the AIC can be used in association with mixed models, it is not common to be used with the models discussed above to select either the optimal set of explanatory variables or other structures.
Hence, finally the four models are compared to select the best one using -2log-likelihood comparison technique.
In all models, to select significant variables, first the main effect and main effect by time interaction were incorporated to the initial candidate model and, then avoid non-significant and so on (Back ward selection technique).
Results
Baseline information and descriptive statistics of CD4+ cell counts: A total of 222 adult ART HIV-1+ patients (1047observations) were used with a minimum of one and maximum of nineteen measures of CD4+ cell counts per individual patients were included in this study. Out of these ART patients, 131(59%) were female patients and 91(41%) were male patients, 175(78.8%) were living around rural out of Hossana town and 47(21.2%) were living around urban centers including Hossana town, the mean and standard deviation of baseline CD4+ cell counts are 355.891 and 321.455 cells per milliliter of blood, respectively.
Exploratory analysis for CD4+ cell counts data: The first step in any model-building process is exploratory data analysis as done below.
Figure 1 shows that there is high variation in CD4+ cell counts at the baseline than at the end in both sex, but the variation of CD4+ cell counts in female is more pronounced than in male and the same feature can seen as for Figure 2 above. Thus, between and within-subject specific difference in variation can’t be ignored.
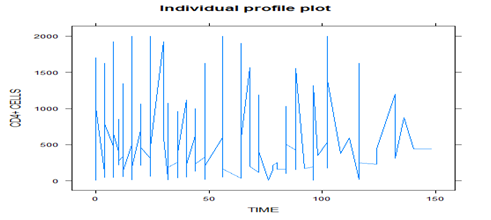
The loess smooth curve, as shown in Figure 3, suggests that the average profile of CD4+ cell counts has a linear relationship over time and almost fairly constant around below 500 cells per milliliter of blood. It indicates that CD4+ cell counts show a slight increasing pattern over time, but the rate of increasing is very low. And also it indicates the linear time effects to be included as fixed-effects in the model.
Statistical models for data analysis: Since the response variable in this study is counts and the data is over dispersed as the variance of CD4+ cell counts (94710.06) is greater than the mean(438.511), the Poisson model is fitted including different random effects(gamma and normal) to handle both over dispersion and correlation, respectively. The (Table 1) displays the comparison among four models, GLM (Poisson model without random effect to handle over dispersion), GLMM (Poisson model with normal random effects to oversee the correlation), Poisson model with the gamma random effects (negative-binomial model) to grip extra variation in the data, and Poisson-normal-gamma model, model with both normal and gamma random effects to discuss about both correlation and over dispersion simultaneously.
CD4+ Cell Counts [Mean (St.d) & %] |
||||
Variables |
Levels |
Mean(St.d) |
% |
Total |
Baseline CD4+ cell counts |
- |
355.891(321.455) |
- |
222 |
Age of Patients |
- |
31.067(8.521) |
- |
222 |
Educational level of Patients |
No education |
288.000(66.30) |
25.67 |
57 |
Primary |
489.491(323.71) |
44.1 |
98 |
|
Secondary |
409.077(279.44) |
23.4 |
52 |
|
Tertiary |
444.469(328.37) |
6.76 |
15 |
|
Sex of Patients |
Female |
338.061 (330.467) |
59 |
131 |
Male |
381.560(308.00) |
41 |
91 |
|
Marital Status of Patients |
Never married |
432.714(416.537) |
15.8 |
35 |
Married |
331.335(276.971) |
57.7 |
128 |
|
Widowed |
369.500(352.421) |
10.8 |
24 |
|
Divorced |
323.526(347.029) |
8.6 |
19 |
|
Separated |
402.312(349.103) |
7.2 |
16 |
|
Religion of Patients |
Muslim |
567.730(355.185) |
11.7 |
26 |
Orthodox |
376.333(371.689) |
28.4 |
63 |
|
Protestant |
337.969 (286.336) |
53.6 |
119 |
|
Catholic |
317.400(174.321) |
2.3 |
5 |
|
Other |
437.222(385.016) |
4.1 |
9 |
|
Employment Status of Patients |
Unemployed |
289.666(245.476 |
25.7 |
57 |
Employed |
1072.000(453.234) |
27 |
60 |
|
Working full time |
331.641(261.385) |
17.6 |
39 |
|
Other |
383.687(335.383) |
29.73 |
66 |
|
Adherence to any of the Drugs |
No |
349.758 (306.857) |
70.7 |
157 |
Yes |
370.707(356.357) |
29.3 |
65 |
|
WHO Stage of the Disease |
I |
359.416(332.894) |
27 |
60 |
II |
413.873(323.824) |
32 |
71 |
|
III |
333.647(317.347) |
30.6 |
68 |
|
IV |
233.478(269.075) |
10.4 |
23 |
|
Area of the Patients |
Rural |
364.595(358.506) |
21.2 |
47 |
Urban |
353.554(311.835) |
78.8 |
175 |
|
Total |
100 |
222 |
||
Table 1 Summary of the baseline characteristics
* Estimates which are not significant at 5% level of significance.
Clearly, both the negative-binomial model and the P-N-G model are important improvements, in terms of the likelihood, relative to the P-N model and ordinary P– model. But in P-N-G model, there is a very strong improvement in fit when gamma and normal random effects are simultaneously allowed for as also the over dispersion parameter, Variance RIS (d) is significant (P=0.0208). Implying the presence of considerable extra variability due to the grouped nature of the data, which is beyond what can be accommodated by the combined model. All covariates in the model except, time sex interaction in P-N-G model and sex in P-G and P-N-G model are significant in all models for the progression of CD4+ cell counts of ART patients.
Therefore, the P-N-G model is a more viable candidate, substantiated further by the abovementioned likelihood comparison.
The random slope model strongly improves the fit of the model based on the likelihood comparison. The estimates and standard errors of the covariates are similarly significant in both models for the response variable. All the normal random effects in the slope model are significant implying that the correlation among subjects is evident.
*Estimates which are not significant at 5% level of significance. Combined model=Poisson-normal-gamma model.
Allowing for the extension of the P-N-G model to include both random intercept and random slope does not improve the fit based on the likelihood comparison. The estimates of the covariates in both models are more or less similar, except an improvement in the slope model for the time sex interaction and sex. Time has a linear relationship with CD4+ cell count, which is what we observed in the graph showing the average trend. The random intercept P-N-G model is chosen based on likelihood comparison.
A retrospective longitudinal study was conducted at Hossana Queen Elleni Mohamad Memorial Hospital, SNNPR, Ethiopia to determine the appropriate model for CD4+ cell counts and to characterize the time course of CD4+ cell progress with the software package, SAS procedure.
The data was unbalanced because some subjects were not keeping the regular time schedule and they were measured at different time points and the number of measurements was different across a subject which is similar to Vernon et al.7 The time scale was used in a monthly format though a six months interval schedule was not worked for some patients which might be reluctance of subjects to follow up. The data was analyzed by version SAS 9.2 using PROC NLMIXED procedure that fits nonlinear mixed models—that is, models in which both fixed and random effects enter nonlinearly. PROC NLMIXED fits nonlinear mixed models by maximizing an approximation to the likelihood integrated over the random effects. This makes the approach to analyze data of this study unlike to other studies done on CD4+ cell counts.
As the result of this study reveals that the mean and standard deviation of CD4+ cell counts per milliliter of blood are not consistent with the result of the study conducted by Gezahegn8 at Durame and Hosanna hospital found. This disagreement in result may be due to the sample size the study included, due to it was made at two different hospitals and due to differences in educational and socio-economic levels. Exploratory data analysis reveals that there is a time trend in the data and the average profile of CD4+ cell counts has a little linear relationship over time which is unlike the SAS sasuser aids data analyzed using linear mixed model by Michael.9 This difference may be due to smoothing technique, time scale, number of observations, and progressive pattern of baseline CD4+ cell counts. However, in this current study, this could not affect the random effect structure to be included in the model. Thus, no improvement in the analysis when non-linearity was assumed and hence, as shown from the relationship a linear time effect was studied on CD4+ cell counts.
Most of the patients were females and they had lower mean CD4+ cell counts than males before ART was initiated which is similar to Moges et al.10 This is because females are biologically and socially more vulnerable to HIV infection in the developing countries. However, this is inconsistent with Kumarasamy et al.11 reported from India. This difference could be due to several reasons as described in that study; HIV associated TB could be the contributing factor for the low CD4+ count in males as the proportion of patients having TB was significantly higher in male HIV positive patients than females. In addition, it may be due to a sex-related difference in the overall CD4+ counts among males and females. HIV sero-negative Ethiopian females had relatively higher CD4+ cell counts than HIV sero-negative males like reported by Yanis et al.17 and Tsegay et al.13
Most of the HIV infected patients enrolled in this study were living around rural out of Hossana town as found out by Nuredin14 in another study at Adama hospital and most of the patients were young mean age of 31 years old who were sexually more active and thus have a higher risk of infection which is comparable to the study conducted by Moges et al.10 at Zewuditu Hospital Addis Ababa, Ethiopia. These findings as found by these authors could conform as previous reports from elsewhere in Ethiopia which reported that HIV prevalence decreases significantly to increasing level of education as well as their socio economic status.
The data in this study indicates that the majority of HIV patients started antiretroviral treatment with more advanced immunodeficiency status. Since the majority of HIV patients had AIDS as defined by their CD4 cell counts < 200 cells/μl, indicating advanced immune suppression at initiation of ART. This was significantly higher when compared to the studies conducted in Nigeria, south eastern United States and Thailand which reported a lower rate of AIDS at the initiation of ART.15,16 Therefore, in the hospital of this current study, delayed enrollment in ART program could be attributed by several factors such as due to fear of stigma. In Ethiopia, as described by the above authors, only one third of HIV infected persons disclosed their HIV status to their partner further compromising the utilization of the counseling and testing and ART services. A similar observation was made among South Africans where patients stared ART program with advanced immunodeficiency status. These findings indicate urgent need to promote early and enhanced HIV testing to enable HIV/AIDS patients to benefit from the expanding ART services.17
Using stepwise selection technique, enter and remove, and backward technique, the most non-significant covariates are removed and the rest in the model are refitted and so on. At the last step the procedure ends with (the most likely selected covariates): time since month of seroconversion, age of the patients, and sex of the patient. Except sex time interaction term in the model, the other covariates, time since month of seroconversion and age of patient are significant for the change in the CD4+ cell counts of ART patients at HAART which was supported by.10,14
Thus, as in many other diseases, age is an important prognostic factor in HIV infection. Age at sero-conversion and age at a given CD4 cell count were shown to be important determinants of progression and survival before the widespread introduction of HAART, starting in 1996.18 This supports the current study. One study is reviewed which supports the significance of gender like this study, but it showed no difference among male and female. Thus, no differences in HIV progression and response to HAART attributable to gender among patients accessing the Spanish hospital network.19 This difference may attribute to method of data analysis used in that study, Kaplan-Meier and Cox regression were used to assess the effect of sex on time to AIDS, survival from AIDS and attribute to other factors.
The comparison among four models were made, GLM (Poisson model without random effect to handle over dispersion), GLMM (Poisson model with normal random effects to administer the correlation), Poisson model with the gamma random effects to grip extra variation in the data, and Poisson-normal-gamma model, model with both normal and gamma random effects to capture both correlation and over-dispersion simultaneously. Estimation was done by maximum likelihood using numerical integration over the normal random effects, if present as was done by Molenberghs et al.16
As Kassahun et al.20 summarized, based on Molenberghs et al.,21 it is argued that the normal and non-normal, a gamma random effect, can usefully be integrated together into a single model to induce association between repeated Poisson data and to correct for the over-dispersion.
One possible route to deal with over-dispersion is to introduce an over-dispersion parameter and only specify a relationship between the mean and the variance, and then apply quasi-likelihood, whereby the extra variability in the data could captured by the dispersion parameter which is as Wedderburn22 did. For the count data, it is common to combine Poisson distribution with a gamma distributed random effect, so that the unconditional distribution of the outcome turns out to be a negative binomial distribution, SAS procedure NLMIXED displayed this as shown on Table 2 (fifth column).23–25 On the other hand, focusing on hierarchical data, the GLM is usually extended to generalized linear mixed models (GLMMs), with a subject-specific random effect, typically a Gaussian form, added in the linear predictor to take into custody a hierarchy-induced association or to account for over-dispersion,3–5 displayed on Table 3 fourth column. As used by Kassahun et al.20 and Molenberghs et al.21 proposed a flexible and unified modeling structure, termed the Poisson-normal-gamma model, to simultaneously capture over-dispersion and correlation for a wide range of clustered data, including count, binary and time-to-event. Thus, two sets of random effects were brought together. The normally distributed subject specific-random effects take into custody the correlation, while a conjugate measurement-specific random effect on the natural parameter, is used to accommodate over-dispersion, as shown on Table 2 last column.
Models |
|||||
Effects and parameters |
Poisson |
Poisson-normal |
Poisson-gamma |
Poisson- normal-gamma |
|
Effects |
Parameters |
Estimate (Se.) |
Estimate (Se.) |
Estimate (Se.) |
Estimate (Se.) |
Intercept |
β1 |
6.055(0.038) |
6.050(0.067) |
6.131(0.081) |
6.136(0.087) |
Time |
β1 |
0.002(0.001) |
0.002(0.001) |
-0.005 (0.002) |
-0.006(0.003) |
Age |
β2 |
-0.006(0.001) |
-0.006(0.001) |
0.004(0.002) |
0.004(0.002) |
Sex |
β3 |
0.052(0.004) |
0.052(0.004) |
0.073(0.058)* |
0.071(0.061)* |
Sex*Time |
β1 |
-0.004(0.001) |
0.093(0.031) |
-0.004 (0.002) |
-0.003(0.002)* |
Sigma |
σ |
0.550(0.030) |
1.568E-8(0.082) |
- |
0.164(0.036) |
Negative-binomial parameter |
α |
- |
- |
2.170(0.089) |
2.287(0.101) |
1/ alpha |
β |
- |
- |
0.460(0.019) |
0.437(0.019) |
Variance RIS |
d |
- |
2.46E-16(-) |
- |
0.027(0.012) |
−2log-likelihood |
- |
151870 |
151975 |
14536 |
14527 |
Table 2 Comparison of Poisson, Poisson-gamma, Poisson-normal and Poisson- normal-gamma Models
Molenberghs & Verbeke,4 considered a Poisson-normal model with random intercepts as well as random slopes in time. It is interesting to note that, when allowing for such an extension in our models, the random slopes improve the fit of the Poisson-normal model, but not of the Poisson-normal-gamma model (details are shown in Table 3 & Table 4). Recall that the same procedure was applied, too, by Booth et al.26,27 While in this study it is considered four different models; but those authors focused on the Poisson-normal and Poisson-normal-gamma implementations. There are further differences in actual fixed-effects and random effects models considered.
Models |
|||
Effects and parameters |
Poisson-normal(random intercept only) |
Poisson-normal (with random intercept& slope) |
|
Effects |
Parameters |
Estimate (Se.) |
Estimate (Se.) |
Intercept |
β1 |
6.026(0.038) |
6.072(0.007) |
Time |
β1 |
0.003(0.001) |
0.004(0.000) |
Age |
β2 |
-0.006(0.001) |
-0.004(0.001) |
Sex |
β3 |
0.102(0.005) |
0.042(0.004) |
Sex*Time |
β1 |
-0.002(0.002) |
-0.003(0.001) |
Normal Random Effect |
b |
-1.188(0.099) |
- |
var(b1) |
d11 |
- |
0.145(0.002 ) |
Var(b2) |
d22 |
- |
0.001(1.552E-6) |
Cov(b1,b2) |
d12 |
- |
-0.004(0.001) |
−2log-likelihood |
- |
151689 |
137475 |
Table 3 Comparison of P-N-model among random effects
Models |
|||
Effects and parameters |
Combined model(with no random effect) |
Combined model(random effect) |
|
Effects |
Parameters |
Estimate (Se.) |
Estimate (Se.) |
Intercept |
β1 |
6.136(0.087) |
5.876(0.006) |
Time |
β1 |
-0.006(0.003) |
0.003(0.001) |
Age |
β2 |
0.004(0.002) |
-0.006(0.001) |
Sex |
β3 |
0.071(0.061)* |
0.106(0.005) |
Sex*Time |
β1 |
-0.003(0.002)* |
-0.002(0.001) |
Negative-Binomial Parameter |
α |
2.287(0.102) |
2.170(0.089) |
1/ alpha |
β |
0.438(0.019) |
0.461(0.019) |
Variance RIS |
d |
- |
0.027(0.012) |
Theta_1 |
θ |
- |
0.089(0.001) |
−2log-likelihood |
- |
14527 |
152476 |
Table 4 Comparison of P-N-G model without and with random effects
Therefore, as tried out to lay the ground to talk, the four models were compared based on their likelihoods since they are not nested to use AIC though some authors used. Accordingly, as was discussed by Kassahun et al.,20 the Poisson-normal-gamma model which combines both normal and gamma random effects to capture together both over-dispersion and correlation was selected to improve the fit to the model based on −2log-likelihood which is 14527.
NB:- CD4+ cell counts is to mean the CD4 cell counts after a patient is tested and notified that he/she is HIV positive, i e., CD4 cell counts after the first visit.
Recommendation
The following were the limitations of the study;
Above all, I would like to thank my almighty God for he allowed me to live and availed his mercy to move and breath, as the result of this, to achieve every of my activities on this land.
My special gratitude goes to Wondewosen Kassahun (Assistant Professor, PhD), my major advisor and instructor, for his kind support, advice, guidance and constructive comments beginning from the proposal development up to the final work of this thesis.
Likewise, I am sincerely grateful to my co-advisor Mr. Abdisa Gurmessa, head department of statistics, for his valuable suggestions, supports and comments beginning from the proposal development up to the final work of this thesis.
Author declares that there are no conflicts of interest.

©2016 Tekle, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.
2 7