
Research Article Volume 12 Issue 1
Revisiting the partition of a set of numerical variables through a mixture of Watson distribution on the n-sphere and underlying factor analysis model
Paulo Gomes 
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

IMS, Nova University of Lisboa, Portugal
Correspondence: Paulo Gomes, IMS, Nova University of Lisboa, Portugal
Received: December 30, 2022 | Published: February 8, 2023
Citation: Gomes P. Revisiting the partition of a set of numerical variables through a mixture of Watson distribution on the n-sphere and underlying factor analysis model . Biom Biostat Int J. 2023;12(1):15-21. DOI: 10.15406/bbij.2023.12.00377
Download PDF
Abstract
A key step of any statistical multivariate analysis concerns the choice of variables in line with the main objectives of the study. Usually, the available procedures to face this problem are restricted to a-posteriori statistical analysis, using Bayesian approaches or stepwise selection procedures.
The main objective of the present paper is to revisit a framework where the a-priori choice of variables makes sense under specific conditions and to propose a factor analysis model particularly adapted to structured quantitative big data.
We have associated our complete sample of variables to a mixture of two bipolar Watson distributions defined on the n-sphere,
,
, where
is a direction parameter and
is a concentration parameter. The likelihood estimates of the direction parameter
is just the first principal component associated of a PCA of cluster i. The identification of the mixture of Watson distribution was obtained by cluster analysis, namely a previous hierarchical cluster analysis followed by a k-means partition of the global sample of variables.
These multivariate data were explained by an alternative factor analysis model potentially delivering directly interpretable solutions without the need of rotations procedures.
The loadings of this factorial model were obtained by regression. The final results concerning communalities of the 16 variables showed that for a great part of them unit variance was quite well explained by the factorial model.
Keywords: big data, cluster analysis, common factor and residual model, principal component analysis, radioactivity effect, sampling variables, Watson distribution
Abbreviations
CA, cluster analysis; CFRM, common factor and residual model; ML, maximum likelihood; PCA, principal components analysis, IVPCA, instrumental variables principal component analysis
Introduction
Over the last decades, advanced technologies in computer and data science have achieved considerable progress in developing statistical or data mining techniques adapted to analyse structured or non-structured big data. Independently of the different domains covered by the concept of “big data”, nowadays it is quite common to have datasets where the number of variables is much larger than the number of observations. Several applications of high dimensional datasets were analysed in astronomy, chemometrics, climate, finance and genomic.1–3
In the present paper the focus will cover situations where the number of observations is pre‐defined, attending the concrete nature of the study, and the randomness concern the choice of variables from a universe of variables following a certain probabilistic model. Such challenge was firstly presented by Hotelling in the context of principal component analysis4 and later by Escoufier Y5 about the sampling of vectorial variables5 and by Gomes in the context of directional probabilistic models associated to an universe of standardized variables defined on the n‐dimensional sphere.6 Later Vigneau et al.7 have proposed to cluster numerical variables about estimated latent variables, using a k-means type algorithm, obtained a classical factor model estimator in each cluster, being the first principal component of the cluster as a centroid. Such approach was extended to latent variables belonging to a space spanned by external variables, in the context of instrumental variables, in the context of instrumental variables principal component analysis (IVPCA) and multivariate partial least square (PLS) regression.
Recently Xavier B. gave a new contribution for clustering numerical and categorical variables under the hypothesis of a mixture of Von Mises Fisher distributions defined on the n-sphere.8
Our paper concerns a cluster analysis of a sample of standardized variables based on a similarity measure of variables j and k defined by
Where
represents the Pearson linear correlation coefficient between variables j and k.
An exponential family of axial distribution defined on the n-spere is an obvious distribution to generate a “bundle of variables” with a given level of interrelation.
The selection of variables from identified sub-groups is, per se, an auspicious way to simplify the learning process of a large set of variables and implicitly leads to a natural dimension reduction, where the first principal component may reflect the “privileged direction” that summarizes sub-groups of variables. These procedures have several applications by reducing the redundancy of variables previously considered for a specific statistical multivariate study, for instance to eliminate certain explanatory variables in a multiple regression model where the multicollinearity problem is present.
In our approach, each sub-group of variables identified by cluster analysis, hierarchical cluster analysis followed by-k-means partition methods9 or EM algorithm10 is considered coming from an axial distribution on the sphere
, the Watson distribution which f.d.p. is defined by
,
Where
is the confluent hypergeometric function defined by
Where
is the Tau function,6
is a directional parameter, and
is the concentration parameter. So, each sample of variables bounded by a “double cone” is supposed a sample of a Watson distribution on the n-spere
, i=1,…K.
Consequently, the global sample is a realization of a random vectorial variable having as distribution a mixture of Watson distributions. Additionally, a focused statistical analysis must be made concerning other isolated variables detecting if they are potential discordant variables under the hypothesis of such distributional mixture previously identified, evaluating the effective role of such variables in view of their nature and the study’s objectives.11
Our proposal is no longer related to the well-known problem of “choice of variables à posteriori” but with the choice of variables a priori supposing the goodness of fit to the proposed probabilistic model under the particular context of quantitative variables where the statistical standardization of data makes sense.12
From likelihood estimators of parameters
, i=1,…,k we have proposed the formulation of an alternative factorial model.
Where the columns of matrix F are the directional parameters
,
is the loading matrix and
the residual matrix which include noise and variables generally weakly correlated with factors and so demanding further statistical analysis facing the previous objectives of a specific study.
The proposed model was applied in multiple contexts13,14 being an alternative factorial model called factorial model in common factors and residuals (FCFR). The performance of this model is illustrated in the present paper using the so-called Amiard Fish data under radioactivity.
Methods
Study sample
The weapons testing program of several nations regardless of the type of blast, has increased the radioactivity of the seas.
The present study concerns the metabolism of radio strontium of fishes. Strontium, if radioactive, may influence the blood cell formation of many fishes. Over the last decades it has been clearly demonstrated that several fission products are potential hazards from a public health point of analysis. The classical data described here was delivered by Amiard laboratory, related to the Aquatic Ecotoxicology research developed during the last decades.15
The sample was divided into three aquariums under the same conditions of radioactivity. However, the three aquariums were subject to increase durations of contact with the radioactive pollutant:
is the aquarium with fishes numbered 1 to 8.
contains fishes numbered 9 to 17.
And contains fishes numbered 18 to 24. Fish 17 died during the experiment.
Each fish was referenced by 16 characteristics divided into two groups, the first nine measured at the end of the experiment
Group 1 – Radioactivity characteristics:
Variable 1 – eye radioactivity
Variable 2 – gill radioactivity
Variable 3 – radioactivity of capping
Variable 4 – fin radioactivity
Variable 5 – liver radioactivity
Variable 6 – radioactivity of digestive tract
Variable 7 – kidneys radioactivity
Variable 8 – scale radioactivity
Variable 9 – muscle radioactivity and
Group 2 – Size features:
Variable 10 – weight
Variable 11 – length
Variable 12 – standard length
Variable 13 – head width
Variable 14 – width
Variable 15 – muzzle width
Variable 16 – eye diameter
Statistical analysis
The strong heterogeneity of empirical standard deviations of variables under study, from a minimum of 0.96 (variable 16) to a maximum of 259.09 (variable 6), would justify a previous identification of potential multivariate outliers using the minimum covariance determinant criteria. However, considering the main objectives of our study we have just standardized our data, giving the same weight to each variable.
Hence the variables will be represented on a sphere (23 active observations). A hierarchical cluster analysis of the sixteen variables followed by a k-means partition, identified two clusters of variables 6: nine radioactivity variables (Group 1) and seven size variables (Group 2).
This means that we have associated our complete sample of variables to a mixture of two Watson distributions.
In the context of sampling variables, the goodness of fit methods for the bipolar Watson distribution was applied to check if the clusters of variables obtained by the previous algorithms come from a Watson distribution.
If x comes from a bipolar Watson distribution,
, then for large
it was shown16 that
. Simulation statistical research have shown that approximation to
distribution it works for moderate values of
.6
The parameters
, i=1,2 were estimated by ML method: the estimate
is just the first principal component of group i, (i=1,2) and
is obtained from the equation
17 were:
is the highest eigenvalue of principal components of group i, i=1,2,
is the number of variables of group i and
is defined by
17
So the factor matrix
.can be written by
where
and
are not, in general, orthogonal vectors.
Our main objective is to construct an alternative factor analysis model
where
is the matrix of loading
and
is the residual matrix
which contains variables supposed not correlated with the factors.
The estimation of loadings was obtained by regression giving the coordinates of variables along the privileged direction generated by vectors
.
Let be
the standardized data set and considering the theoretical correlation matrix
defined by
So
And the term
will be estimated by
The diagonal elements of this estimated term will give the communalities of our factor analysis model, and so the part of the unit variances of the original variables that were explained by the model.
The elements out of the diagonal of this matrix will give the linear correlation between variables reproduced by our model.
Finally, representing by
the empirical correlation matrix,
Results
Identification of a mixture of Watson distribution
Previous hierarchical cluster analysis showed that it was quite realistic to consider just two groups of variables, so that from an arbitrary initial partition into two clusters of equal size, we have achieved a local optima solution using a variant k-means method “la méthode des nuées dynamiques” where the distance function is defined by
A stable solution was obtained at the fourth interaction
Group1: radioactivity variables
Group2: size variables
The first principal component of standardized variables of group 1 is the ML estimate of directional parameter
and the respective concentration parameter
was estimated by
where
is highest eigenvalue of group 1’s PCA,
, giving
Hence the inertia explained by first principal component is 55.86%.
Similarly,
is the first principal component of PCA of group 2 and
is the solution of equation
were
is highest eigenvalue of such PCA giving
. The inertia explained by the first principal component is now equal to 84.16%
Representation of observations on the first principal plan
The factor matrix
allowed the representation of fishes on the first factorial plan (Table 1 & Figure1). The linear correlation coefficient between
and
,
, explain the non-orthogonality of factors.
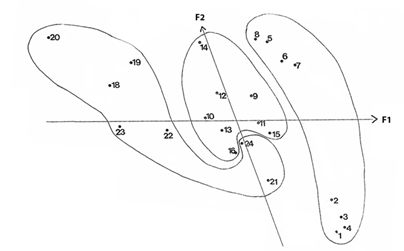
Figure 1 Representation of fishes on first factorial plan.
Observation |
Factor 1 |
Factor 2 |
1 |
0.186 |
-0.398 |
2 |
0.211 |
-0.286 |
3 |
0.22 |
-0.345 |
4 |
0.227 |
-0.383 |
5 |
0.185 |
0.26 |
6 |
0.208 |
0.199 |
7 |
0.243 |
0.189 |
8 |
0.15 |
0.273 |
9 |
0.064 |
0.078 |
10 |
-0.096 |
0.003 |
11 |
0.068 |
-0.004 |
12 |
-0.028 |
0.093 |
13 |
-0.057 |
-0.034 |
14 |
-0.022 |
0.266 |
15 |
0.094 |
-0.044 |
16 |
-0.044 |
-0.118 |
18 |
-0.364 |
0.114 |
19 |
-0.267 |
0.188 |
20 |
-0.494 |
0.268 |
21 |
0.022 |
-0.218 |
22 |
-0.238 |
-0.027 |
23 |
-0.352 |
-0.005 |
24 |
-0.003 |
-0.074 |
Estimation of loadings and representation of variables on the first factorial plan
The loadings of our model (Table 2) were estimated by regression obtaining the coordinates of variables along the two privileged directions (Figure2) and the communalities, so the part of unit variance of each variable explained by the model.
Variables |
Factor 1 |
Factor 2 |
Communalities |
1 |
-0.93 |
0.048 |
0.898 |
2 |
-0.958 |
-0.066 |
0.878 |
3 |
-0.947 |
-0.128 |
0.828 |
4 |
-0.942 |
-0.026 |
0.871 |
5 |
-0.609 |
0.197 |
0.495 |
6 |
-0.342 |
0.034 |
0.126 |
7 |
-0.345 |
-0.561 |
0.297 |
8 |
-0.828 |
0.093 |
0.748 |
9 |
-0.464 |
0.027 |
0.225 |
10 |
0.028 |
-0.977 |
0.975 |
11 |
-0.022 |
-0.947 |
0.912 |
12 |
0.017 |
-0.935 |
0.885 |
13 |
0.007 |
-0.955 |
0.918 |
14 |
0.012 |
-0.929 |
0.871 |
15 |
-0.215 |
-0.888 |
0.700 |
16 |
0.114 |
-0.779 |
0.682 |
Table 2 Loading matrix and communalities
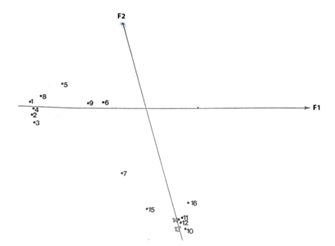
Figure 2 Representation of variables on first principal plan.
From Table 3 we may conclude that, for group 1, all the variables except radioactivity of digestive tract, kidneys and muscle radioactivity, contribute to the first factor. The exam of the communalities show that these variables are not quite well explained by the model.
|
Variables |
Relative contribution to factor 1 |
Relative contribution to factor 1 |
|
1 |
0.178 |
|
|
2 |
0.174 |
|
|
3 |
0.162 |
|
|
4 |
0.173 |
|
CLUSTER 1 |
5 |
0.092 |
|
|
6 |
0.025 |
|
|
7 |
0.004 |
|
|
8 |
0.147 |
|
|
9 |
0.045 |
|
|
10 |
|
0.165 |
|
11 |
|
0.155 |
|
12 |
|
0.150 |
CLUSTER 2 |
13 |
|
0.156 |
|
14 |
|
0.148 |
|
15 |
|
0.112 |
|
16 |
|
0.114 |
Table 3 Relative contributions of variables to factors
We emphasize the fact that the loading matrix reveals the “simple structure” underlying the Amiard data set, where two correlated factors really explain the behaviours of this data set. It means that this model is potentially competitive in such situations, providing directly interpretable solutions, avoiding rotation procedures.
It is quite interesting to check the performance of this model to explain the correlation between variables for each cluster
From
Table 4 & Table 5 compare the original intra linear correlations and the correlations reproduced by the model.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
|
|
|
|
|
|
|
|
2 |
0.882
(0.882) |
|
|
|
|
|
|
|
3 |
0.857
(0.849) |
0.829
(0.851) |
|
|
|
|
|
|
4 |
0.877
(0.882) |
0.825
(0.874) |
0.959
(0.845) |
|
|
|
|
|
5 |
0.700
(0.651) |
0.588
(0.623) |
0.370
(0.590) |
0.497
(0.629) |
|
|
|
|
6 |
0.219
(0.336) |
0.282
(0.329) |
0.288
(0.315) |
0.310
(0.329) |
0.240
(0.246) |
|
|
|
7 |
0.164
(0.116) |
0.173
(0.170) |
0.210
(0.195) |
0.094
(0.150) |
0.006
(0.003) |
0.167
(0.035) |
|
|
8 |
0.743
(0.819) |
0.745
(0.799) |
0.810
(0.766) |
0.832
(0.801) |
0.416
(0.600) |
0.264
(0.307) |
-0.001
(0.081) |
|
9 |
0.378
(0.449) |
0.522
(0.441) |
0.149
(0.424) |
0.239
(0.441) |
0.590
(0.326) |
-0.024
(0.168) |
-0.136
(0.056) |
0.386
(0.410) |
Table 4 Initial linear correlation coefficients between variables of cluster 1 and correlations reproduced by the model in bold
|
10 |
11 |
12 |
13 |
14 |
15 |
11 |
0.938
(0.943) |
|
|
|
|
|
12 |
0.943
(0.929) |
0.953
(0.899) |
|
|
|
|
13 |
0.947
(0.946) |
0.946
(0.915) |
0.931
(0.901) |
|
|
|
14 |
0.933
(0.921) |
0.829
(0.891) |
0.829
(0.878) |
0.862
(0.894) |
|
|
15 |
0.748
(0.797) |
0.762
(0.772) |
0.712
(0.761) |
0.723
(0.777) |
0.680
(0.756) |
|
16 |
0.803
(0.811) |
0.677
(0.784) |
0.629
(0.772) |
0.714
(0.785) |
0.843
(0.765) |
0.621
(0.644) |
Table 5 Original correlation coefficients between variables of cluster 2 and correlations reproduced by the model in bold
Interpretation of factor analysis outputs
The Variables {1,2,3,4,5,8} contribute 92.6% to the inertia associated to first factor. All these five variables are strongly negatively correlated with factor 1. In general terms, the factor explains the “radioactivity effect” on the fishes in direct relationship with the duration of such contamination. So, the fishes with smaller factor score, are the most contaminated and the fishes with larger score are the less radio contaminated (Figure1). Complementary, the “size variables” gave a similar contribution to factor 2 (Table 3) and all of them are strongly negatively correlated with such factor. So, the second factor discriminate the smallest fishes of aquarium 1 {1,2,3,4} from the larger fishes {5,6,7,8}. The factorial representation (Figure 1) doesn’t suggest different levels of contamination in these two groups of fishes, except the effect on Variable 4 (fin radioactivity) where the smallest fishes compared to the largest ones, registered, on average, 20% more contamination. And except Variable 8 (scale radioactivity) where the registered variation, among these two sub-groups was about 55%.
The fishes belonging to aquarium 2 (intermediate duration of radio contamination) presented a relatively homogenous behaviour in relation to first factor (Figure1). However, in this aquarium, fish 14 present a clear isolated position, being the smallest fish of the global sample and become particularity affected at the live and digestive tract level (Table 6).
As it was expected, most of the fishes of aquarium 3 {18,19,20,22, 23} presented the highest degree of contamination (Figure 1). In contrast fish 21 and fish 24 suffered a quit smaller contamination considering that these fishes belong to group of the bigger fishes (Table 6, data set). In fact, our previous statistical analysis pointed out the fact that the two factors are negatively correlated.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
1 |
10 |
65 |
65 |
107 |
7 |
76 |
16 |
142 |
1 |
132 |
214 |
197 |
54 |
47 |
18 |
11 |
2 |
9 |
43 |
39 |
67 |
29 |
113 |
10 |
99 |
2 |
122 |
220 |
198 |
49 |
44 |
16 |
10 |
3 |
6 |
47 |
71 |
95 |
11 |
192 |
9 |
121 |
2 |
129 |
220 |
198 |
49 |
45 |
17 |
11 |
4 |
7 |
70 |
40 |
66 |
8 |
310 |
10 |
90 |
2 |
133 |
225 |
199 |
52 |
48 |
15 |
11 |
5 |
8 |
59 |
67 |
100 |
14 |
289 |
4 |
244 |
1 |
57 |
168 |
149 |
37 |
37 |
9 |
9 |
6 |
8 |
46 |
55 |
112 |
17 |
115 |
8 |
153 |
1 |
59 |
178 |
160 |
38 |
35 |
11 |
9 |
7 |
7 |
47 |
36 |
87 |
16 |
100 |
4 |
162 |
1 |
59 |
176 |
156 |
40 |
36 |
11 |
9 |
8 |
11 |
79 |
46 |
95 |
20 |
106 |
10 |
141 |
4 |
47 |
176 |
165 |
39 |
31 |
10 |
8 |
9 |
13 |
80 |
64 |
155 |
42 |
192 |
9 |
169 |
3 |
72 |
182 |
164 |
40 |
39 |
12 |
10 |
10 |
21 |
150 |
115 |
146 |
49 |
229 |
9 |
233 |
5 |
79 |
200 |
179 |
45 |
38 |
12 |
9 |
11 |
12 |
91 |
84 |
138 |
22 |
590 |
9 |
220 |
2 |
80 |
185 |
163 |
43 |
41 |
12 |
11 |
12 |
14 |
120 |
76 |
125 |
21 |
309 |
9 |
617 |
5 |
72 |
175 |
158 |
40 |
39 |
13 |
10 |
13 |
14 |
142 |
86 |
135 |
34 |
523 |
9 |
211 |
10 |
75 |
189 |
169 |
42 |
39 |
18 |
10 |
14 |
23 |
92 |
80 |
132 |
49 |
459 |
9 |
197 |
2 |
52 |
164 |
147 |
36 |
35 |
12 |
9 |
15 |
13 |
85 |
64 |
124 |
20 |
318 |
9 |
191 |
4 |
86 |
195 |
175 |
41 |
39 |
16 |
10 |
16 |
14 |
106 |
67 |
110 |
31 |
115 |
9 |
248 |
6 |
87 |
210 |
170 |
46 |
40 |
17 |
10 |
18 |
32 |
224 |
260 |
314 |
36 |
107 |
13 |
461 |
3 |
72 |
181 |
164 |
41 |
36 |
13 |
9 |
19 |
22 |
162 |
218 |
318 |
25 |
884 |
5 |
590 |
2 |
63 |
175 |
160 |
38 |
35 |
12 |
9 |
20 |
31 |
195 |
208 |
350 |
73 |
109 |
5 |
809 |
11 |
49 |
170 |
154 |
39 |
33 |
12 |
8 |
21 |
15 |
127 |
119 |
197 |
23 |
99 |
7 |
157 |
2 |
107 |
204 |
185 |
47 |
45 |
15 |
11 |
22 |
22 |
160 |
256 |
282 |
12 |
102 |
11 |
690 |
3 |
83 |
190 |
176 |
42 |
44 |
14 |
9 |
23 |
24 |
162 |
231 |
308 |
51 |
1031 |
17 |
558 |
2 |
82 |
194 |
168 |
42 |
39 |
14 |
10 |
24 |
19 |
64 |
163 |
229 |
16 |
109 |
8 |
345 |
1 |
91 |
190 |
172 |
44 |
42 |
13 |
11 |
Discussion and conclusion
The starting focus of a classical factor analysis is the correlation matrix which describes the interrelation between the variables under study. The classical factor analysis is defined by:
Where F is the matrix of the latent variables supposed non-correlated and potentially enable to explain a great part of the correlation between the observed variables. In this model, the residual matrix V contains unknown non-correlated variables and also not correlated with the latent variables, representing the specific component of each one of the original variables. The loading matrix informs about the importance of latent factors in their relationship with the variables of the model.
Such hypothesis lead to the results
where
being
the variance and covariance matrix.
In practical terms if R is the empirical correlation matrix, the main objective of classical factor analysis model is to find the loadings A and the estimate of variance and covariance of residual terms in order to minimize the difference between R and
.
Joreskog18 studied the relative performance of alternative approaches to such optimization problems, namely by the comparison of least square method where we have:
Min
with
and generalized least squares where we have:
Min
with
Or by the maximum likelihood method where we have:
Min
with
In the context of large sample sizes, the classical properties of ML estimators have shown the relative preference of this last choice, under the hypothesis of an approximately underlying multinormal distribution of observations. Implicitly, such factor analysis model uses a rational to justify a specific choice of the variables, in general quite connected with the objectives and the priorities of the statistical study.
In the present paper we have supposed that the statistical study doesn’t justify any sampling from individuals because they are previously quite well defined. So, the real problem concerns how to sample variables, namely where we have a very big number of variables. First of all, the treatment of quantitative structured multivariate data suggests a variable cluster analysis procedure just to try to downgrade the problem’s complexity. It means to identify sub-clusters of variables especially intercorrelated. The described framework leads us to the formulation of a probabilistic distribution model associated to each sub-cluster previously identified. In the context of a large number of variables from quantitative structured data, the usual heterogeneity of statistical descriptive indicators or units of measure, justified the previous standardization of data. So it was quite obvious to think about a probabilistic model defined on the sphere n-dimensional,
: The bipolar Watson distribution
with a direction parameter
and a concentration parameter
seemed to be a natural model to explain the stochastic behaviour of each sub-cluster of variables. The fact that the ML estimate
of was the first principal component of PCA of sub-cluster i, gave the basis to propose a factorial model derived from the identification of a mixture of Watson distribution on the n-sphere.
The potential presence of some variables considered as statistical discordant in relation to any Watson component of the mixture, justifies a specific statistical analysis to investigate their incorporation in the model facing the main objective of the study. Or eventually asking for an adequate transformation if we are detecting a non-linear correlation with some of the remaining variables. Sometimes it could be more adequate to consider such transformed variable as supplementary variables, so not included on the construction of factors, but afterword’s projected on the factorial plan if the linear correlation coefficients with each factor have some statistically significant meaning. The proposed model
where
is such that the factors are not necessarily orthogonal vectors, meaning that our approach is enables to deliver outputs directly interpretable without a specific rotation procedure.
We have no analytic results to calculate the convenient size of each sub-sample in order to stabilize the associate factor, depending on the value of the concentration parameter and on the dimension of n-spere. However, the simulation work already developed constitutes an interesting platform to face such problem in practical terms.6
Recent developments extending our research to qualitative variables7 clearly shows the renewed interest of this topic in the age of big data.
There is yet an interesting open problem regarding the joint sampling of individuals and variables in Hilbert spaces.
Acknowledgments
Conflicts of interest
The author declares that there are no conflicts of interest.
Funding
References
- Clarke R, Resson H, Wang A, et al. The properties of high-dimensional data spaces: implications for exploring gene and protein expression data. Nature Rev cancer. 2008;8(1):37–49.
- Johson RA, Wichern D W. Applied multivariate data analysis. 6th ed. New Jersey, USA: Prentice Hall; 2007.
- Johsonstone I M, Titterington DM. Statistical challenge of high dimensional data. Phil Trans R Soc A. 2009;367:4237–4253.
- Hotelling H. Analysis of a complex of statistical variables into principal components. J Educ Psychol. 1933;24:417–441.
- Escoufier Y. These de Doctorat d’État Sciences. France; 1970.
- Gomes P. Distribution de Bingham sur la n-spere: une nouvelle approache de l’analyse fcatorielle. France; 1987.
- Vigneau E, Qannari EM. Clustering of variables around latent components. Communication in Statistics–simulation and computations. 2003;32:1131–1150.
- Bry X, Cucala L. A von Mises-fisher mixture model for clustering numerical and categorical variables. Advances in Data Analysis. 2022;16(2):429–455.
- Diday E. A new method in automatic classification and pattern recognition the method of dynamic clouds. Journal of Applied Statistics. 1971;19(2):19–33.
- Figueiredo A, Gomes P. Performance of the EM algorithm on the identification of a mixture of distributions defined on the hypersphere. 2006.
- Figueiredo A, Gomes P. Discordancy test for the bipolar Watson distribution defined on the hypersphere. Communication in Statistics – simulation and computations. 2006;145–153.
- Bert DJ. Goodness-of-fit and discordancy tests for samples from the Watson distribution on the sphere. Austral Statistics. 1986;28(1):13–31.
- Figueiredo A, Gomes P. Clustering of variables based on Watson distribution on hypersphere: a comparation of algorithms. Communication in Statistics – simulation and computation. 2015;2622–2635.
- Figueiredo A, Gomes P. Classificação de variáveis definidas na hiperesfera através de um modelo de mistura. Proceeding SPE congress. Porto. 2012.
- Triquet C, Amiard J Mouneyrac C. Aquatic ecotoxicology – Advancing tools for dealing with emerging risks. 1st ed. Elsevir Science. 2015.
- Mardiak V. Statistics of directional data. London: Academic Press; 1972.
- Gomes P. Contribution to the problem of the choice of variables in PCA. Montpellier, France: Technical Report nº 8505; 1985.
- Joreskog KG. Factor analysis by least squares and maximum likelihood methods in statistical methods for digital computers. Wiley. 1977.

©2023 Gomes. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


