Research Article Volume 6 Issue 1
Rani distribution and its application
Rama Shanker
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
Correspondence: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea
Received: May 19, 2017 | Published: May 30, 2017
Citation: Shanker R. Rani Distribution and Its Application. Biom Biostat Int J. 2017;6(1):256‒265 DOI: 10.15406/bbij.2017.06.00155
Download PDF
Abstract
In the present paper, a new one parameter lifetime distribution named, “Rani Distribution’ has been proposed for modeling lifetime data from engineering and biomedical sciences. Its various statistical and mathematical properties including its shapes for varying values of parameter, moments and moments based measures, hazard rate function, mean residual life function, stochastic ordering, deviations from the mean and the median, Bonferroni and Lorenz curves, order statistics , Renyi entropy measure and stress-strength reliability have been studied. Both the maximum likelihood estimation and the method of moments have been discussed for estimating the parameter of the proposed distribution. A simulation study has been carried out and results are presented. A numerical example has been presented to test the goodness of fit of the proposed distribution and it has been found that it gives much closer fit than almost all one parameter lifetime distributions introduced in statistical literature.
Keywords: lifetime distributions, statistical and mathematical properties, parameter estimation, goodness of fit
Introducton
In the present world the modeling and analyzing lifetime data are essential in almost all applied sciences including medicine, engineering, insurance and finance, amongst others. The two classical one parameter lifetime distributions which are popular and are in use for modeling lifetime data from biomedical science and engineering are exponential and Lindley introduced by Lindley.1 Shanker, et al.,2 have detailed comparative study on modeling of lifetime data from various fields of knowledge and observed that there are many lifetime data where these two distributions are not suitable due to their shapes, nature of hazard rate functions, and mean residual life functions, amongst others. In search for new one parameter lifetime distributions which gives better fit than exponential and Lindley distributions, recently Shanker has introduced several one parameter lifetime distributions in statistical literature namely Akash,3 Shanker,4 Aradhana,5 Sujatha,6 Amarendra,7 Devya,8 Rama9 and Akshaya10 and showed that these distributions gives better fit than the classical exponential and Lindley distributions. The probability density function (pdf) and the corresponding cumulative distribution function (cdf) of Akash[3], Shanker,4 Aradhana,5 Sujatha,6 Amarendra,7 Devya,>8 Rama9 and Lindley1 distributions are presented in Table (1). It has also been discussed by Shanker that although each of these lifetime distributions has advantages and disadvantages over one another due to its shapes, hazard rate functions and mean residual life functions, there are still many lifetime data where these distributions are not suitable for modeling lifetime data from theoretical or applied point of view. Therefore, an attempt has been made in this paper to obtain a new lifetime distribution which is flexible than these one parameter lifetime distributions for modeling lifetime data in reliability and in terms of its hazard rate shapes.
The new one parameter lifetime distribution is based on a two-component mixture of an exponential distribution having scale parameter
and a gamma distribution having shape parameter 5 and scale parameter
with their mixing proportion
.
The probability density function (p.d.f.) of a new one parameter lifetime distribution can be introduced as
(1.1)
We would call this distribution, “Rani distribution”. This distribution can be easily expressed as a mixture of exponential
and gamma
with mixing proportion
. We have
where
.
The corresponding cumulative distribution function (c.d.f.) of (1.1) can easily be obtained as
(1.2)
The graphs of the p.d.f. and the c.d.f. of Rani distribution for varying values of the parameter
are shown in Figures 1 & 2. The p.d.f. of Rani distribution is monotonically decreasing.
Distributions |
Probability density functions and cumulative distribution functions |
Akash |
pdf |
|
cdf |
|
Shanker |
pdf |
|
cdf |
|
Aradhana |
pdf |
|
cdf |
|
Sujatha |
pdf |
|
cdf |
|
Amarendra |
pdf |
|
cdf |
|
Devya |
pdf |
|
cdf |
|
Rama |
pdf |
|
cdf |
|
Akshaya |
pdf |
|
cdf |
|
Lindley |
pdf |
|
cdf |
|
Table 1 pdf and cdf of Akash, Shanker, Aradhana, Sujatha, Amarendra, Devya, Rama, Akshaya and lindley distributions for
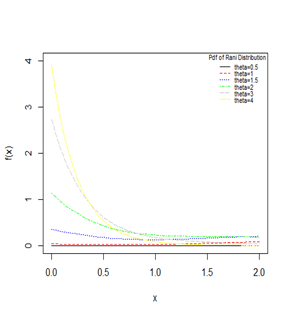
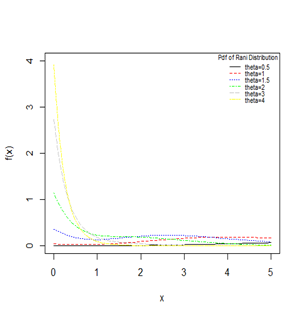
Figure 1 Graphs of the pdf of Rani distribution for varying values of the parameter
.
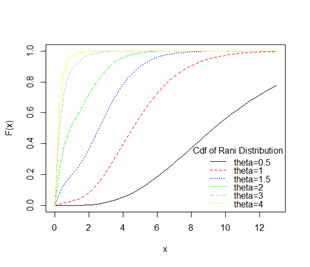
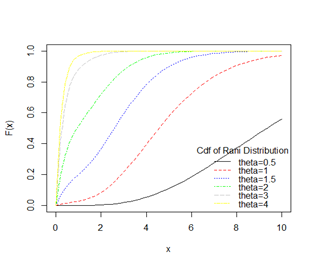
Figure 2 Graphs of the cdf of Rani distribution for varying values of the parameter
.
Moments and moments based measures
The moment generating function of Rani distribution (1.1) can be obtained as
Thus the
th moment about origin
, obtained as the coefficient of
in
, of Rani distribution can be given by
(2.1)
Substituting
, the first four moments about origin of Rani distribution are obtained as
,
,
,
Now using relationship between central moments and moments about origin, the central moments of Rani distribution are obtained as
The coefficient of variation
, coefficient of skewness
, coefficient of kurtosis
and index of dispersion
of Rani distribution are thus obtained as
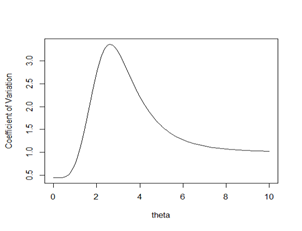
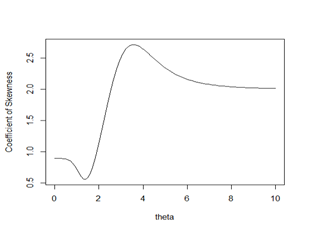
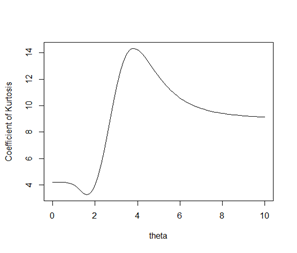
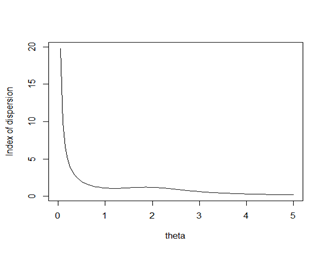
The nature of coefficient of variation, coefficient of skewness, coefficient of kurtosis and index of dispersion of Rani distribution have been shown graphically for varying values of parameter in
Figure (3). The condition under which Rani distribution is over-dispersed, equi-dispersed, and under-dispersed along with condition under which Akash,
3 Rama
9 Akshaya,
10 Shanker,
4 Amarendra,
7 Aradhana,
5 Sujatha
6 Devya,
8 Lindley
1 and exponential distributions are over-dispersed, equi-dispersed, and under-dispersed are presented in
Table (2).
Distribution |
Over-dispersion
|
Equi-dispersion
|
Under-dispersion
|
Rani |
|
|
|
Akash |
|
|
|
Rama |
|
|
|
Akshaya |
|
|
|
Shanker |
|
|
|
Amarendra |
|
|
|
Aradhana |
|
> |
|
Sujatha |
> |
|
|
Devya |
|
|
|
Lindley |
|
|
|
Exponential |
|
|
|
Table 2 Over-dispersion, equi-dispersion and under-dispersion of Rani, Akash, Rama, Akshaya, Shanker, Amarendra, Aradhana, Sujatha, Devya, Lindley and exponential distributions for parameter
Hazard rate function and mean residual life function
Let
and
be the p.d.f. and c.d.f of a continuous random variable
. The hazard rate function (also known as the failure rate function) and the mean residual life function of a continuous random variable
are, respectively, defined as
(3.1)
and
(3.2)
The corresponding hazard rate function,
and the mean residual life function,
of the Rani distribution are obtained as
(3.3)
and
(3.4)
It can be easily verified that
and
. It is also obvious from the graphs of
and
that the shapes of
is increasing, decreasing and upside bathtub, whereas the shapes of
is decreasing, increasing
and downside bathtub. The graphs of the hazard rate function and mean residual life function of Rani distribution are shown in Figure (4).
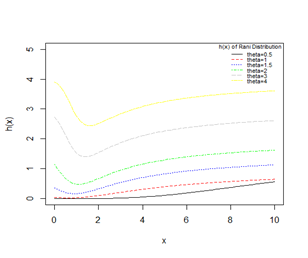
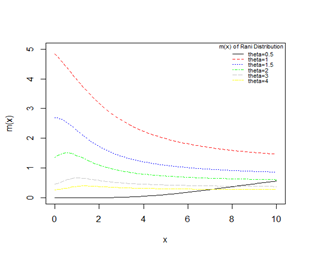
Figure 4 Graphs of
and
of Rani distribution for varying values of the parameter
.
Stochastic orderings
Stochastic ordering of positive continuous random variables is an important tool for judging their comparative behavior. A random variable
is said to be smaller than a random variable
in the
- stochastic order
if
for all
- hazard rate order
if
for all
- mean residual life order
if
for all
- likelihood ratio order
if
decreases in
.
The following results due to Shaked and Shanthikumar [11] are well known for establishing stochastic ordering of distributions
(4.1)
Rani distribution is ordered with respect to the strongest ‘likelihood ratio’ ordering as shown in the following theorem.
Theorem: Suppose
Rani distributon
and
Rani distribution
. If
, then
and hence
,
and
.
Proof: We have
Now
.
This gives
Thus for
,
. This means that
and hence
,
and
.
Mean deviations
The amount of scatter in a population is measured to some extent by the totality of deviations usually from mean and median. These are known as the mean deviation about the mean and the mean deviation about the median defined as
and
, respectively, where
and
. The measures
and
can be calculated using the simplified relationships
(5.1)
and
(5.2)
Using p.d.f. (1.1) and expression for the mean of Rani distribution (1.1), we get
(5.3)
(5.4)
Using expressions from (5.1), (5.2), (5.3), and (5.4), the mean deviation about mean,
and the mean deviation about median,
of Rani distribution (1.1) are obtained as
(5.5)
(5.6)
Bonferroni and lorenz curves
The Bonferroni and Lorenz curves12 and Bonferroni and Gini indices have applications not only in economics to study income and poverty, but also in other fields like reliability, demography, insurance and medicine. The Bonferroni and Lorenz curves are defined as
(6.1)
and
(6.2)
respectively or equivalently
(6.3)
and
(6.4)
respectively, where
and
.
The Bonferroni and Gini indices are thus defined as
(6.5)
and
(6.6)
respectively.
Using p.d.f. of Rani distribution (1.1), we have
(6.7)
Now using equation (6.7) in (6.1) and (6.2), we have
(6.8)
and
(6.9)
Now using equations (6.8) and (6.9) in (6.5) and (6.6), the Bonferroni and Gini indices are obtained as
(6.10)
(6.11)
Order statistics and renyi entropy measure
Distribution of order statistics
Let
be a random sample of size
from Rani distribution (1.1). Let
denote the corresponding order statistics. The p.d.f. and the c.d.f. of the
th order statistic, say
are given by
and
,
respectively, for
.
Thus, the p.d.f. and the c.d.f of
th order statistics of Rani distribution are given by
and
Renyi entropy measure
Entropy of a random variable
is a measure of variation of uncertainty. A popular entropy measure is Renyi entropy [13]. If
is a continuous random variable having probability density function
, then Renyi entropy is defined as
where
.
Thus, the Renyi entropy for the Rani distribution (1.1) is obtained as
Stress-strength reliability
The stress-strength reliability gives the idea about the life of a component which has random strength
that is subjected to a random stress
. When the stress applied to it exceeds the strength, the component fails instantly and the component will function satisfactorily till
. Therefore,
is a measure of the component reliability and in statistical literature it is known as stress-strength parameter. It has wide applications in almost all areas of knowledge especially in engineering such as structures, deterioration of rocket motors, static fatigue of ceramic components, aging of concrete pressure vessels etc.
Let
and
be independent strength and stress random variables having Rani distribution (1.1) with parameter
and
respectively. Then the stress-strength reliability
of Rani distribution can be obtained as
.
Estimation of parameter
Maximum likelihood estimate (MLE)
Let
be a random sample from Rani distribution (1.1). The likelihood function,
of (1.1) is given by
The natural log likelihood function is thus obtained as
.
Now
, where
is the sample mean.
The MLE
of
is the solution of the equation
and thus it is the solution of the following nonlinear equation
Method of moment estimate (MOME)
Equating the population mean of Rani distribution (1.1) to the corresponding sample mean, MOME
, of
is the solution of the following six degree polynomial equation
.
A Simulation study
In this section, a simulation study has been carried out to know the efficiency of the maximum likelihood estimate(MLE) of Rani distribution. The simulation study is based on Acceptance/Rejection method.
Acceptance/Rejection algorithm:
To simulate from the density
, it is assumed that we have envelope density
from which it can simulate and that we have some
such that
.
Step 1. Simulate
from
Step 2. Generate
, where
Step 3. If
, then return
, otherwise go to step 1
The simulation study is based on generating
samples of size
for
using above algorithm. Then we calculate the following measures
(i) Average bias of the simulated estimate
, where
is the ML estimate
(ii) Average mean square error (MSE)
.
The average bias and average mean square error (MSE) for each of the ML estimate has been calculated and shown in Table (3), where MSE has been shown in bracket.
|
|
|
|
|
50 |
0.05034 |
0.026212 |
0.010078 |
-0.00079 |
-0.12673 |
-0.03435 |
-0.01008 |
|
100 |
0.025405 |
0.132465 |
0.005188 |
-0.00033 |
-0.06454 |
-0.01755 |
-0.00269 |
|
150 |
0.017098 |
0.008916 |
0.003523 |
-0.0002 |
-0.04385 |
-0.01193 |
-0.00186 |
|
200 |
0.012992 |
0.006755 |
0.002713 |
-0.00012 |
-0.03376 |
-0.00913 |
-0.00147 |
|
Table 3 Average bias and average mean square error of the simulated estimate
The graphical presentation of MSE for different values of parameter is shown in Figure 5.
Goodness of fit
In this section, the goodness of fit of Rani distribution has been discussed with a real lifetime data set from engineering and the fit has been compared with one parameter lifetime distributions namely Akash,3 Shanker,4 Amarendra,7 Aradhana,5 Sujatha,6 Devya,8 Lindley1 and exponential. The data set is the strength data of glass of the aircraft window reported by Fuller, et al.,14 and are given as 18.83, 20.80, 21.657, 23.03, 23.23, 24.05, 24.321, 25.50, 25.52, 25.80, 26.69, 26.77, 26.78, 27.05, 27.67, 29.90, 31.11, 33.20, 33.73, 33.76, 33.89, 34.76, 35.75, 35.91, 36.98, 37.08, 37.09, 39.58, 44.045, 45.29, 45.381. In order to compare lifetime distributions, values of
, AIC (Akaike Information Criterion) and K-S Statistic ( Kolmogorov-Smirnov Statistic) for the above data set have been computed and presented in Table (4).
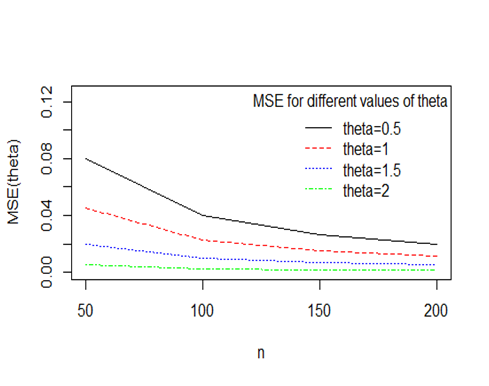
Figure 5 Graphs of MSE for different values of
and
.
The formulae for computing AIC and K-S Statistic are as follows:
,
, where
= the number of parameters,
= the sample size and
is the empirical distribution function. The best distribution is the distribution which corresponds to lower values of
, AIC, and K-S statistic and higher p-value. The MLE
with the standard error, S.E
of
,
, AIC, K-S Statistic and p-value of the fitted distributions are presented in the Table (4). It can be easily observed from above Table (3) that Rani distribution gives better fit than the fit given by Akash,3 Rama,9 Akshaya,10 Shanker,4 Amarendra ,7 Aradhana,5 Sujatha,6 Devya8 Lindley1 and exponential distributions and hence it can be considered as an important lifetime distribution for modeling lifetime data over these distributions.
Concluding remarks
A one parameter lifetime distribution named, “Rani distribution” has been proposed. Its statistical properties including shapes, moments, skewness, kurtosis, index of dispersion, hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves and stress-strength reliability have been discussed. The condition under which Rani distribution is over-dispersed, equi-dispersed, and under-dispersed are presented along other one parameter lifetime distributions. Maximum likelihood estimation and method of moments have been discussed for estimating its parameter. A simulation study has been presented. Finally, the goodness of fit test using K-S Statistic (Kolmogorov-Smirnov Statistic) and p-value for a real lifetime data has been presented and the fit has been compared with some one parameter lifetime distributions.
NOTE: The paper is named “Rani distribution” in the name of my lovely niece Rani Kumari, second daughter of my respected eldest brother Professor Shambhu Sharma, Department of Mathematics, Dayalbagh Educational Institute, Dayalbagh, Agra, India.
Distributions
|
|
S.E
|
|
AIC |
K-S |
p-value |
Rani |
0.162278 |
0.013034 |
227.25 |
229.25 |
0.223 |
0.0775 |
Akash |
0.097065 |
0.010048 |
240.68 |
242.68 |
0.298 |
0.0059 |
Rama |
0.129782 |
0.011651 |
232.79 |
234.79 |
0.253 |
0.0301 |
Akshaya |
0.125745 |
0.011292 |
234.44 |
236.44 |
0.263 |
0.0223 |
Shanker |
0.647164 |
0.0082 |
252.35 |
254.35 |
0.358 |
0.0004 |
Amarendra |
0.128294 |
0.012413 |
233.41 |
235.41 |
0.257 |
0.0269 |
Aradhana |
0.094319 |
0.00978 |
242.22 |
244.22 |
0.306 |
0.0044 |
Sujatha |
0.095613 |
0.009904 |
241.5 |
243.5 |
0.303 |
0.0051 |
Devya |
0.160873 |
0.012916 |
227.68 |
229.68 |
0.422 |
0 |
Lindley |
0.062992 |
0.008001 |
253.98 |
255.98 |
0.365 |
0.0003 |
Exponential |
0.032449 |
0.005822 |
274.52 |
276.53 |
0.458 |
0 |
Table 4 MLE’s, S.E - 2ln L, AIC and K-S statistics of the fitted distributions of the given data set
Acknowledgements
Conflicts of interest
References

©2017 Shanker. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.