A life table is an essential tool for valuing life insurance policies and it presents the probability distribution of the future life–time of a group of lives at the various ages. They are developed by the experts with actuarial knowledge. The life table will vary with the group of lives considered in the mortality investigation. Further the variation may also prevail when the same group of lives is investigated at different time periods, due to the effect of generational change in mortality. In this paper we apply statistical inference on published life tables for the Kenyan mortality experience for the mortality investigations performed during two separate disjoint time periods, to investigate significance of the variation in the mortality as the periods of the investigation vary. It is shown that the variation in the probability distribution of the future life–time for the Kenyan mortality experience is significant. Thus we confirm, as known in practice by the actuaries, that there is a need for continuous mortality investigations and the construction of the corresponding life tables, every after some time interval, to account for the variation in mortality as generations vary.

Keywords: life table, curtate future life–time, probability mass function, cumulative distribution function, goodness–of–fit tests, kenyan mortality experience

Consider a life aged x and let K(x) denote the curtate future life–time of the life, that is the time left before he or she dies, in completed years, see Gerber.¹ Then K(x) is a discrete random variable with K(x)= 0, 1, .. $[\omega -1]$ where $\omega$ is the assumed limiting age, such that $[\omega -1]$is the maximum age a life can live and the operation [.] refers to 'integer part' of the object. The probability mass function for K(x), P(K(x)=k), k=0, 1,2,… ,.. $[\omega -1]$can be derived from a life table as noted in Section 2. Let $Fk(x)$(r) denotes the corresponding distribution function. To compare two separate mortality experiences, let$Fk\text{'}(x)$denote the distribution function corresponding to the other experience. Then to compare the distributions, the hypotheses are given by$Fk(x)$.

$H_0:F_{K(x)}\left(r\right)=F_{k’(x)}$

Versus

$$H_a:NOT{H}_0$$

The non–parametric goodness–of–fit tests can be used to carry out the test given appropriate data, Gibbon.² However, as in Benjamin et al.³ given the relevant life tables, we have the equivalent hypothesis test, namely to test

$H^I{}_0:$The Life table corresponding to $Fk(x)$(r) is the same as the Life table corresponding to $Fk\text{'}(x)$(for all real values, r)

Versus

$H^I{}_a:NOT{H}^I{}_0$

Tests for $H^{I}0$versus $H^I{}_a$can be performed using available published life tables for a mortality experience of a given population, Benjamin et al.³ and Scott.⁴ These are goodness–of–fit tests, which include the chi–square test, and the other specific goodness–of–fit tests that address the limitations encountered when the former test is applied.^3,4 The specific tests include the standardized deviation test, the ordinary signs test and the cumulative deviations test. In the methodology section these tests are discussed. Results on the goodness–of–fit tests then follow. Conclusion and recommendation from the study are discussed in the paper.

Consider a life table, Gerber.¹ The table has two main columns: ‘Age, x’ (column 1) and ‘Number of lives aged x,$l_x$'(column 2). A third column for ‘Number of deaths aged x ’, $d_x$ may also be included in the table. However the third column can be derived from the second column. Thus the life table functions, $l_x$and $d_x$ form the basis of a life table. Note that the $l_x$and the $d_x$ functions of the age x, are standard life table discrete functions applied in actuarial science to denote the number of lives and deaths at age x, respectively, in a life table.

Let K(x) denote the curtate (completed years) future life – time for a life aged x , last birthday. Then clearly K(x) = 0, 1, 2, …. $[\omega -1]$Which is a random variable, at any age x, with the probability mass function given by Gerber.¹

$P(K(x)=k)=\frac{d_{x+k}}{l_x},\forall k\mathrm{.................................}(2.1)$

Thus the cumulative distribution function for K(x), say$Fk(x)$(y) is given by

$F_{K(x)}(y)={\displaystyle \sum _{k=0}^{y}P(K(x)=k)={\displaystyle \sum _{k=0}^y\frac{d_{x+k}}{l_x}}}\mathrm{..............}(2.2)$

The null hypothesis

For two cohorts of lives their corresponding mortality experiences can be represented by the random variables K(x) and K’(x) with cumulative distributions,$Fk(x)$(y) and $Fk\text{'}(x)$(y) respectively. To test for equality of the distributions, the null hypothesis is given by

$H_0:F_{K(x)}\left(y\right)=F_K{’}_{(x)}\left(y\right)$, for all values of y.

We note, from Equation (2.2), that this hypothesis is equivalent to the hypothesis

$H{’}_0:$The life table for K(x) is the same as the life table for K’(x)

To test$H{’}_0:$against an alternative we use the approach for comparing a standard life table with another life table as in Benjamin et al.³ and Scott.4

Note that we can have the null hypothesis stated as follows;

$H{’}_0:$Underlying mortality rates of each age x for the experience is the same as the corresponding rates in the standard table.

The alternative hypothesis is given by

$H{’}_1:$NOT $H{’}_0$

The following assumptions are made in the study:

1. The tests are carried out on data for the age range 24 to 65 years in order to make the analysis consistent with the nature of the data. This is based on the general assumption that a majority of the population only purchase life assurance products after 24 years, the average age at entry into employment, and before 65 years, which is the average retirement age.⁵
2. We test the hypothesis at 5% level of significance.

Statistical tests for goodness–of–fit

The differences in mortality experiences can be investigated by carrying out the following statistical for a given level of significance.

1. The Chi–Square Test
2. The Individual Standardized Deviations (ISD) Test
3. The Ordinary Signs Test
4. Cumulative Deviation Test

The chi–square test: The chi–square statistic also known as the overall test may be defined as:  

${\chi }^2={\displaystyle {\sum }_{all intervals}\frac{{\left(Actual-Expected\right)}^2}{Expected}}$

This is the sum of the squares of the standardized deviations of the probability of death at each age x.

1. Lives (lx) are independent with respect to mortality experience
2. The expected number of deaths at each age is large (>5)

Where Actual, denoted by A = the number of deaths, dx, in the table 2007–2010. Expected, denoted by E =the number of deaths, dx, in the table 2000–2003. The chi–square statistic has n degrees of freedom, where n is the total number of ages which in this case n=42. Let the confidence interval be 95%, therefore, the null hypothesis is rejected if the calculated value of the test statistic is greater than the tabulated chi–square value at level of significance$\alpha =\mathrm{0.05.}$If the computed chi–square statistic is large, we conclude that there is significant difference between the observed and the expected number of deaths. The chi square test has various limitations.^3,4 It fails to detect the following.

1. A number of excessively large of deviations neutralized by an excessively large number of small deviations. This can be remedied by the individual standardized deviations test.
2. The signs of the deviations which can be remedied by doing a signs test
3. Any patterns of deviation signs. This can be remedied by the runs test.
4. A large cumulative deviation over the age range. This can be remedied by the cumulative deviations test.

The following discussion on these specific goodness–of–fit tests follow, as in Benjamin et al.³ and Scott.⁴

Individual standardized deviations (ISD) test: The ISD test is used to correct the defect of the Chi–Square Test whereby it fails to detect a number of excessively large deviations. Moreover, the ISD test seeks to determine whether the observed pattern of the individual standardized deviations is consistent with a standard normal distribution. The assumption made when using the ISD test is that the normal approximation is a suitable approximation at all ages. We test the null hypothesis that the pattern of the ISDs follows the standard normal distribution. First, the standardized deviations Zx for each age x were obtained, where each Zx = (A – E) /E, where A and E are as defined in Section 4.2.1, at age x. The real line is divided into eight intervals:

(–$\infty$, –3), (–3, –2), (–2, –1), (–1, 0), (0, 1), (1, 2), (2, 3), (3,$\infty$)

The count of the number of standardized deviations, $Z_x’s$, which fall into each interval is noted. To obtain the number of deviations which should fall into the “expected” category, we use a general rule for the ISD test, that the expected number of deviations should not be less than 5 in each interval. One is therefore required to sometimes pool data of adjacent cells in the table to achieve this requirement (Table 1).

The ${\chi }^2$ statistic can be obtained as follows.

$${\chi }^2={\displaystyle {\sum }_{all intervals}\frac{{\left(Actual-Expected\right)}^2}{Expected}}$$

This statistic will have (r – 1) degrees of freedom where r = number of groups. There ought to be a nearly equal number of positive and negative values. An excess of either positive or negative values shows that the data is skewed and has a positive bias or a negative bias, respectively. Further, if the standardized deviations do not adhere to a normal distribution, then the mortality experiences are different.

Ordinary signs test: The ordinary signs test is an overall test for bias to test whether the mortality rates are too high or too low. It deals with the defect of chi–square test where it fails to detect an imbalance between the number of positive and negative deviations. We expect that if the mortality rates of the two tables are consistent then roughly, the signs of the deviations have a binomial distribution with parameters n (the total number of ages being considered) and 0.5. This is a two–sided test since we consider both the negative and positive signs. If the number of deviations of either sign is very large compared to the other, then we conclude that the rates are biased. Let K be the number of positive deviations. Under the null hypothesis K~ binomial (n, 0.5).

If n (the total number of ages being considered) is large (>20), we use the approximation

K~ normal (n/2, n/4)

The limitation of signs test is that it is qualitative and not quantitative.

Cumulative deviations test: This method deals with the failure of the chi–square test to detect a large cumulative deviation over the age range. It detects overall bias or log runs of deviations that have the same sign. The assumption of this test is that the normal approximation is reasonable at all ages. The null hypothesis is that the mortality rates are not biased or that the variance is not greater than expected.

Test Statistic:

$$Z=\frac{{{\displaystyle \sum }}_{all age ranges}\left(Actual-Expected\right)}{\sqrt{{{\displaystyle \sum }}_{all age ranges}Expected}}$$

This is a two–tailed test. We test at 5% level of significance. If the absolute value of the calculated statistic is greater than 1.96, we reject the null hypothesis and conclude that the mortality rates are such the two sets of data are significantly different.

Data

The data are the secondary data which appear in the published Kenya Mortality Tables, namely the 2000–2003 Kenyan Mortality Life Table and the 2007–2010 Kenyan Mortality Life Table appear in Appendix A1, as given in AKI (2018). Published life tables for a given group of lives are readily available in the public domain in most economies where they exist. They are useful in actuarial and demographic applications, among others.

Exploratory data analysis

The graphs in Figure 1 and Figure 2 reveal existence of some differences in the mortality rate for the two separate mortality investigations. The significance of the difference is studied in Section 5.2 (Figure 1).

Figure 1 shows that there is a general shift of the curve to the right as we move from the 2000–2003 life table mortality to the 2007–2010 life table mortality and as we move from men mortality to female mortality rates. This implies an improvement in mortality, that on average, lives have a higher chance of surviving at each age, for the age groups affected. The mortality for men in the 2000–2003 life table remained the higher across all the ages and increases sharply at age 60, compared to the 2007–2010 life table mortality experience. The mortality for women in years 2007–2010 was higher than that of 2007–2010 life table male mortality and 2000–2003 life table female mortality between ages 56 and 80 but lower from age 80. The graphs in Figure 2 further confirm the observations from Figure 1, emphasizing the age group 20 to 60 years (Figure 2). We test the significance of these differences using the statistical tests in the following section.

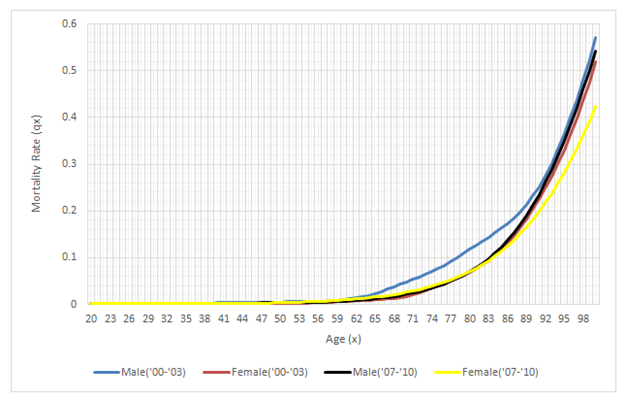
Figure 1 A plot of mortality rate against age for male and female population, age range 20-100.

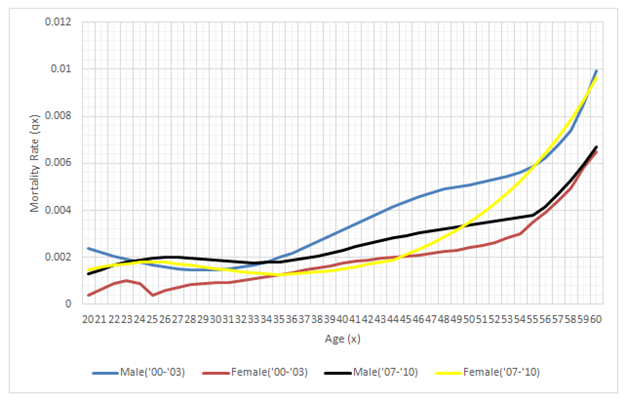
Figure 2 A plot of mortality rate against age for male and female population, age range 20 to 60.

Results on the goodness–of–fit tests

Results are based on the application of the approaches in Section 2 on the Kenyan mortality experience secondary data available in form of the published mortality life tables, AKI (2018). Four test statistics, namely the chi–square test, the individual standardized deviation (ISD) test, the ordinary sign test and the cumulative deviations test are applied. These tests are considered in Section 5.2.1, Section 5.2.2, Section 5.3.3 and Section 5.3.4 respectively. We consider, in each case, the male lives and the female lives mortality experience separately.

Chi–square test: The tabulated value of the Chi–Square Test (CST) statistic at 0.05 level of significance when the degrees of freedom (n=42) is ${\chi }^2{}_n=\mathrm{55.74.}$The computed values are as determined in from Table A1–1 and Table A1–2 in the Appendix.

Mortality experience for male lives (CST): From Table A1–1, we can easily compute

${\chi }^2={\displaystyle {\sum }_{all intervals}\frac{{\left(Actual-Expected\right)}^2}{Expected}}$= 2272.17

Hence computed ${\chi }^2$ value = 2272.17

Mortality experience for female lives (CST): From Table A1–2, we can easily compute

${\chi }^2={\displaystyle {\sum }_{all intervals}\frac{{\left(Actual-Expected\right)}^2}{Expected}}$= 3223.32

Hence computed ${\chi }^2$ value = 3223.32. The computed ${\chi }^2$ value for both males and females mortality data are greater than the tabulated value. Hence there is sufficient evidence to reject the null hypothesis and thus there could be a significant difference between the two mortality experiences for either male and female lives.

Individual standardized deviations (ISD) Test

Mortality experience for male lives (ISD) (Table 2)

Mortality experience for female lives (ISD): The computed value of the Chi–square statistic for the Males is 76.2619. The computed value of the Chi–square statistic for the Females is 87.40625. The computed values in both cases exceed the upper 95% of the tabulated value of a Chi–Square distribution with 3 degrees of freedom, which are 7.815. Thus, we can conclude that the data does not conform to the standard normal distribution. Hence there is sufficient evidence to reject the null hypothesis and thus there is evidence of significant difference between the two mortality experiences for either male and female lives (Table 3).

Ordinary signs test

The ordinary signs test (OST) addressed the defect of the Chi–Square test where it failed to detect an imbalance between the number of positive and negative deviations observed in the mortality data for assured lives in Kenya. Since the total number of ages under observation (n=42) is large, a normal distribution approximation is assumed for the number of positive deviation, to be denoted by K. Thus, K ~ Normal (21, 10.5)3,4. That is the statistic K has a normal distribution with mean = 21, and variance = 10.5.

Mortality experience for male lives (OST): The number of positive deviations, from Table A1–1, we note that K =32.

To standardize this value:

$$Z=\frac{32-21}{\surd \left(10.5\right)}= 3.395$$

Mortality experience for female lives (OST): The number of positive deviations from Table A1–2, can easily be computed to obtain K =33.

To standardize this value:

$$Z=\frac{32-21}{\surd \left(10.5\right)}= 3.703$$

The ordinary signs test is a two–tailed test. This means that the tabulated value required is the table value for the standardized normal distribution, at a level of significance of 0.025 since the level of significance $\alpha =\mathrm{0.05.}$from the standard normal tables, the table value, denoted by $Z_{0.025}$, is given by $Z_{0.025}=1.96$. Thus by comparison, the Z values computed for both Males and Females mortality data are larger than the tabulated value at 0.05 level of significance. There is therefore sufficient evidence to reject the null hypothesis. This means that there is an imbalance between positive and negative deviations. It can be concluded, from these results, that the mortality rates being compared are significantly different in each case for males and females.

Cumulative deviations test

The cumulative deviations test (CDT) corrects the failure of the chi–square test to detect a large cumulative deviation over the age range. Moreover, the test is a good measure of overall bias.

Mortality experience for male lives(CDT): From Table A1–1, we compute the standardized cumulative deviation value for males data,

$$Z= \frac{{{\displaystyle \sum }}_{all age ranges}\left(Actual-Expected\right)}{\sqrt{{{\displaystyle \sum }}_{all age ranges}Expected}} = \frac{-3115.17}{\surd 13082} = –27.23$$

Mortality experience for female lives (CDT): From Table A1–2, we compute the standardized cumulative deviation value for females data,

$$Z= \frac{{{\displaystyle \sum }}_{all age ranges}\left(Actual-Expected\right)}{\sqrt{{{\displaystyle \sum }}_{all age ranges}Expected}} = \frac{4743}{\surd 11405} = 44.41$$

The cumulative deviations test is a two–tailed test. This means that the tabulated value required is the table value for the standardized normal distribution , at a level of significance of 0.025 since the level of significance α = 0.05. From the standard normal tables, the table value, denoted by $Z_{0.025}$, is given by $Z_{0.025}=1.96$. Thus by comparison, the computed value for both mortality for male and mortality for female lives are larger than the tabulated value at 0.05 level of significance. There is therefore sufficient evidence to reject the null hypothesis. This means that there is an imbalance between positive and negative deviations. Thus the mortality rates being compared are significantly different.

All the tests applied in Section 3 lead to rejection of the null hypothesis that the 2000–2003 Kenya mortality life table and the 2007–2010 Kenya mortality life table are similar, and this imply that there is significant variation in the mortality experience underlying the two life tables. Hence the distribution of the future life–time varies with the period of the mortality investigation for the Kenyan mortality experience. Thus we confirm and recommend that for the life tables to remain relevant they should be developed continuously by having mortality investigations carried out every after some appropriate interval of time.⁶

None.

Author declares that there is no conflict of interest.

1. Gerber HU. Life Insurance Mathematics. 3rd ed. Springer: Swiss Association of Actuaries; 1997:18‒20.
2. Gibbons JD. Non-Parametric Statistical Inference. New York: Graw-Hill Book Company; 1971:(4):68‒73.
3. Benjamin B, Pollard JH. The Analysis of Mortality and Other Actuarial Statistics. 2nd ed. London: William Heinemann Ltd; 1980:222‒236.
4. WF Scott. Mortality Studies. Aberdeen: University of Aberdeen; 2000:81‒83.
5. Brown RL. Issues in the Modelling of Mortality at Advanced Ages. Institute of Insurance and Pension Research, University of Waterloo, Canada; 1997.
6. Report on Kenyan Mortality Life Tables. Association of Kenya Insurers (AKI); 2018.