In this paper, firstly the nature of exponential and Lindley distributions have been studied using different graphs of their probability density functions and cumulative distribution functions. The expressions for the index of dispersion for both exponential and Lindley distributions have been obtained and the conditions under which the exponential and Lindley distributions are over-dispersed, equi-dispersed, and under-dispersed has been given. Several real lifetimes data-sets has been fitted using exponential and Lindley distributions for comparative study and it has been shown that in some cases exponential distribution provides better fit than the Lindley distribution whereas in other cases Lindley distribution provides better fit than the exponential distribution.

Keywords: exponential distribution, Lindley distribution; index of dispersion, estimation of parameter, goodness of fit

The time to the occurrence of some event is of interest for some populations of individuals in every field of knowledge. The event may be death of a person, failure of a piece of equipment, development of (or remission) of symptoms, health code violation (or compliance). The times to the occurrences of events are known as “lifetimes” or “survival times” or “failure times” according to the event of interest in the fields of study. The statistical analysis of lifetime data has been a topic of considerable interest to statisticians and research workers in areas such as engineering, medical and biological sciences. Applications of lifetime distributions range from investigations into the endurance of manufactured items in engineering to research involving human diseases in biomedical sciences.

There are a number of continuous distributions for modeling lifetime data such as exponential, Lindley, gamma, lognormal and Weibull. The exponential, Lindley and the Weibull distributions are more popular in practice than the gamma and the lognormal distributions because the survival functions of the gamma and the lognormal distributions cannot be expressed in closed forms and both require numerical integration. Both exponential and Lindley distributions are of one parameter and the Lindley distribution has advantage over the exponential distribution that the exponential distribution has constant hazard rate and mean residual life function whereas the Lindley distribution has increasing hazard rate and decreasing mean residual life function.

In this paper, firstly the nature of exponential and Lindley distribution has been studied by drawing different graphs for probability densities and cumulative distribution functions for the same values of parameter. Several examples of lifetimes data-sets from different fields of knowledge has been considered and an attempt has been made to study the goodness-of- fit for both exponential and Lindley distributions to see the superiority of one over the other.

Exponential Distribution
The exponential distribution was the first widely used lifetime distribution model in areas ranging from studies on the lifetimes of manufactured items^1-3 to research involving survival or remission times in chronic diseases.⁴ The main reason for its wide applicability as lifetime model is partly because of the availability of simple statistical methods for it² and partly because it appeared suitable for representing the lifetimes of many things such as various types of manufactured items.¹

Let $T$ be a continuous random variable representing the lifetimes of individuals in some population and following exponential distribution. The probability density function (p.d.f.), cumulative distribution function (c.d.f.), survival function, hazard function, and mean residual life function of $T$ , respectively, are given by
$f\left(t\right)=\theta e^{-\theta x};\theta >0,t>0$
$F\left(t\right)=1-e^{-\theta t};\theta >0,t>0$
$S\left(t\right)=1-F\left(t\right)=e^{-\theta t}$
$h\left(t\right)=\frac{f\left(t\right)}{1-F\left(t\right)}=\frac{f\left(t\right)}{S\left(t\right)}=\theta$
<$m\left(t\right)=\frac{1}{\theta }$

Lindley distribution
Lindley distribution is a mixture of exponential $\left(\theta \right)$ and gamma $\left(2,\theta \right)$ distributions with mixing proportion $\frac{\theta }{\theta +1}$  and is given by Lindley (1958) in the context of Bayesian Statistics as a counter example of fiducial Statistics. Let $T$ be a continuous random variable representing the lifetimes of individuals in some population and following Lindley distribution. The probability density function (p.d.f.), cumulative distribution function (c.d.f.), survival function, hazard function, and mean residual life function of $T$ , respectively, are given by
$f\left(t\right)=\frac{{\theta }^2}{\theta +1}\left(1+t\right)e^{-\theta t};\theta >0,t>0$
$F\left(t\right)=1-\frac{\theta +1+\theta t}{\theta +1}{e}^{-\theta t};\theta >0,t>0$
$S\left(t\right)=1-F\left(t\right)=\frac{\theta +1+\theta t}{\theta +1}{e}^{-\theta t}$
$h\left(t\right)=\frac{f\left(t\right)}{1-F\left(t\right)}=\frac{f\left(t\right)}{S\left(t\right)}=\frac{{\theta }^2\left(1+t\right)}{\theta +1+\theta t}$
$m\left(t\right)=\frac{\theta +2+\theta t}{\theta \left(\theta +1+\theta t\right)}$
The Lindley distribution has been extensively studied and generalized by many researchers such as^5-12 are among others. A discrete version of the Lindley distribution has been obtained by^13,14 obtained the Lindley mixture of Poisson distribution.

The graphs of the probability densities functions of exponential and Lindley distributions are presented for different values of parameter and shown in Figure 1. The graphs of the cumulative distribution functions of exponential and Lindley distributions are presented for different values of parameter and are shown in Figure 2.

The expressions for coefficient of variation (C.V.), coefficient of Skewness $\left(\sqrt{{\beta }_1}\right)$ , coefficient of Kurtosis, and index of dispersion of exponential and Lindley distributions are summarized in the following Table 1. It can be easily verified that the Lindley distribution is over- dispersed$\left(\mu <{\sigma }^2\right)$ , equi-dispersed$\left(\mu ={\sigma }^2\right)$  and under-dispersed$\left(\mu >{\sigma }^2\right)$  for $\theta <(=)>{\theta }^{\ast }=1.170086487$  respectively, whereas as exponential distribution is over- dispersed$\left(\mu <{\sigma }^2\right)$ , equi-dispersed$\left(\mu ={\sigma }^2\right)$  and under- dispersed$\left(\mu >{\sigma }^2\right)$  for $\theta <(=)>{\theta }^{\ast }=1$  respectively

The exponential and Lindley distribution has been fitted to a number of real lifetime data - sets to tests their goodness of fit. Goodness of fit tests for fifteen real lifetime data- sets has been presented here.

In order to compare exponential and Lindley distributions,$-2\ln L$ , AIC (Akaike Information Criterion), AICC (Akaike Information Criterion Corrected), BIC (Bayesian Information Criterion), K-S Statistics ( Kolmogorov-Smirnov Statistics) for all fifteen real lifetime data- sets have been computed. The formulae for computing AIC, AICC, BIC, and K-S Statistics are as follows:
$AIC=-2\ln L+2k$ ,$AICC=AIC+\frac{2k\left(k+1\right)}{\left(n-k-1\right)}$ , $BIC=-2\ln L+k\ln L$  and
$D=\underset{x}{\text{Sup}}\left|F_n\left(x\right)-F_0\left(x\right)\right|$ , where $k$ the number of parameters, $n$ is the sample size and $F_n\left(x\right)$ is the empirical distribution function. The best distribution corresponds to lower$-2\ln L$ , AIC, AICC, BIC, and K-S statistics.

The fittings of exponential and Lindley distributions are based on maximum likelihood estimates (MLE). Let $t_1,t_2,\mathrm{....},t_n$  be a random sample of size n from exponential distribution. The likelihood function, $L$  and the log likelihood function, $\ln L$ of exponential distribution are given by $L={\theta }^n{e}^{-n\theta \overline{t}}$  and $\ln L=n\ln \theta -n\theta \overline{t}$ . The MLE $\widehat{\theta }$  of the parameter $\theta$  of exponential distribution is the solution of the equation $\frac{d\ln L}{d\theta }=0$  and is given by $\widehat{\theta }=\frac{1}{\overline{t}}$ , where $\overline{t}$ is the sample mean. Let $t_1,t_2,\mathrm{....},t_n$  be a random sample of size n from Lindley distribution. The likelihood function, $L$  and the log likelihood function,$\ln L$ of Lindley distribution are given by $L={\left(\frac{{\theta }^2}{\theta +1}\right)}^n{\displaystyle \prod _{i=1}^n\left(1+t_i\right)}{e}^{-n\theta \overline{t}}$  and $\ln L=n\ln \left(\frac{{\theta }^2}{\theta +1}\right)+{\displaystyle \sum _{i=1}^n\ln \left(1+t_i\right)}-n\theta \overline{t}$ . The MLE $\widehat{\theta }$  of the parameter $\widehat{\theta }$  of Lindley distribution is the solution of the equation $\frac{d\ln L}{d\theta }=0$  and is given by$\widehat{\theta }=\frac{-\left(\overline{t}-1\right)+\sqrt{{\left(\overline{t}-1\right)}^2+8\overline{t}}}{2\overline{t}};\overline{t}>0$ , where $\overline{t}$ is the sample mean. It was shown by [5] showed that the estimator $\widehat{\theta }$  of Lindley distribution is positively biased, consistent and asymptotically normal.

From above table it is obvious that the fittings of Lindley distribution is better than the exponential distribution in Datasets 1-6,12,14,15. Whereas the fittings of exponential distribution is better than the Lindley distribution in Datasets 7-11,13 (Table 2).

In this paper we have tried to find the suitability of exponential and Lindley distributions for modeling real lifetimes data. It has been observed that neither exponential distribution nor Lindley distribution is appropriate for modeling real lifetime data in all cases. As per the nature of the data related with over-dispersion, equi-dispersion, and under-dispersion, in some cases exponential is better than Lindley while in other cases Lindley is better than exponential. Further, the decision about the suitability of exponential and Lindley for modeling real lifetime data depends on the nature of the data. Of course, Lindley is more flexible than exponential but exponential has some advantage over Lindley due to its simplicity.

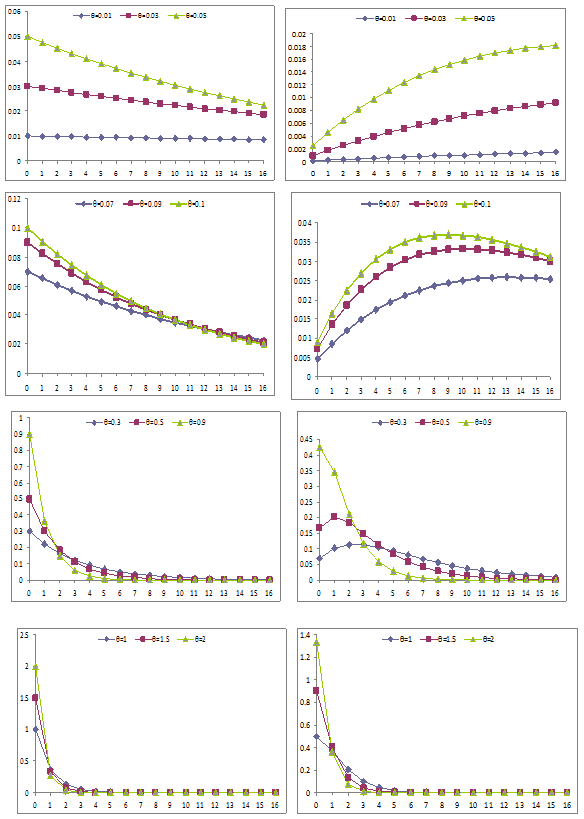
Figure 1 Graphs of the p.d.f. of exponential and Lindley distributions (left hand side graphs are for exponential and right hand side graphs are for Lindley).

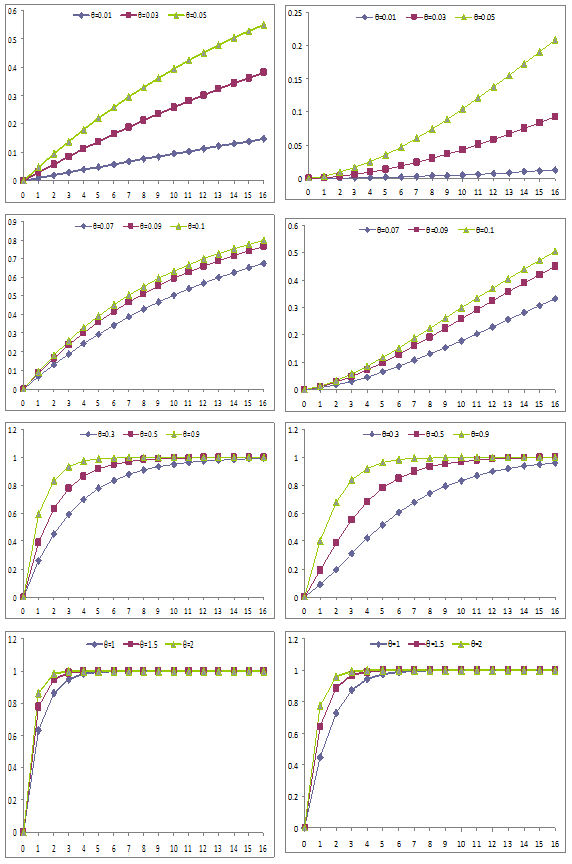
Figure 2 Graphs of the c.d.f. of exponential and Lindley distributions (left hand side graphs are for exponential and right hand side graphs are for Lindley).

Data Set 1 The data set represents the strength of 1.5cm glass fibers measured at the National Physical Laboratory, England. Unfortunately, the units of measurements are not given in the paper, and they are taken from Smith and Naylor.¹⁵

Data Set 2 The data is given by Birnbaum and SaundersM¹⁶ on the fatigue life of 6061 – T6 aluminum coupons cut parallel to the direction of rolling and oscillated at 18 cycles per second. The data set consists of 101 observations with maximum stress per cycle 31,000 psi. The data ( $\times$ ${10}^{-3}$ ) are presented below (after subtracting 65).

Data Set 3 The data set is from Lawless.¹⁷ The data given arose in tests on endurance of deep groove ball bearings. The data are the number of million revolutions before failure for each of the 23 ball bearings in the life tests and they are:

Data Set 4 The data is from Picciotto¹⁸ and arose in test on the cycle at which the Yarn failed. The data are the number of cycles until failure of the yarn and they are:

Data Set 5 This data represents the survival times (in days) of 72 guinea pigs infected with virulent tubercle bacilli, observed and reported by Bjerkedal.¹⁹

Data Set 6 This data is related with behavioral sciences, collected by N Balakrishnan et al.²⁰ The scale “General Rating of Affective Symptoms for Preschoolers (GRASP)” measures behavioral and emotional problems of children, which can be classified with depressive condition or not according to this scale. A study conducted by the authors in a city located at the south part of Chile has allowed collecting real data corresponding to the scores of the GRASP scale of children with frequency in parenthesis, which are:

Data Set 7 The data set reported by Efron²¹ represent the survival times of a group of patients suffering from Head and Neck cancer disease and treated using radiotherapy (RT).  

Data Set 8 The data set reported by Efron²¹ represent the survival times of a group of patients suffering from Head and Neck cancer disease and treated using a combination of radiotherapy and chemotherapy (RT+CT).

Data Set 9 This data set represents remission times (in months) of a random sample of 128 bladder cancer patients reported in Lee and Wang.²²

Data Set 10 This data set is given by Linhart and Zucchini,²³ which represents the failure times of the air conditioning system of an airplane:

Data Set 11 This data set used by Bhaumik et al.,²⁴ is vinyl chloride data obtained from clean upgradient monitoring wells in mg/l:

Data Set 12 This data set represents the waiting times (in minutes) before service        of 100 Bank customers and examined and analyzed by Ghitany et al.⁵ for fitting the Lindley²⁵ distribution.

Data Set 13 This data is for the times between successive failures of air conditioning equipment in a Boeing 720 airplane, Proschan:²⁶

Data set 14 This data set represents the lifetime’s data relating to relief times (in minutes) of 20 patients receiving an analgesic and reported by Gross and Clark.²⁷

Data Set 15 This data set is the strength data of glass of the aircraft window reported by Fuller et al.:²⁸

Acknowledgments

Conflicts of interest