Malnutrition among children under age five is the major public health delinquent issue in the developing world, particularly in Ethiopia. This study aimed to figure out determinants of Ethiopian children malnutrition by applying Bayesian approach with Markov chain Monte Carlo (MCMC) techniques on the 2011 EDHS data. The preliminary analysis indicated that the overall prevalence of underweight among children in Ethiopia is found 36.4%. Bayesian generalized additive regression model applied to flexibly estimate effects of socio-economic, demographic, health and environmental covariates. The estimation result showed that covariates succeeding birth interval, gender of child, child by choice not by chance, vaccination and cough are significantly affect the children nutritional status in Ethiopia. The effect of child age, mother’s age at child birth, succeeding birth intervals, number of household member and birth order were also explored non-parametrically as determinants of children nutritional status. Based up on this biometric analysis, concerned governmental and non-governmental bodies should give emphasis on the significant covariates to improve the children nutritional status of the country.

Keywords: children nutrition, malnutrition, arthrometric measurement, MCMC, generalized bayesian additive model and ethiopia

Malnutrition stays one of the most commonplace reasons of morbidity and mortality amongst children less than five years antique kids all through the World.¹ Worldwide over 10 million children beneath the age of 5 years die every year from preventable and treatable ailments regardless of effective health interventions. At least half of these deaths are because of malnutrition. Malnourished children have reduced resistance to infection; consequently, they’re much more likely to die from common youth illnesses inclusive of diarrheal illnesses and respiratory infections. In addition, malnourished children that live on are likely to suffer from frequent infection, which adversely affects their nutritional repute and locks them into a vicious cycle of recurring illness, In growing international locations, malnutrition is a primary health hassle.²

The burden of malnutrition is much higher in South Asia compared to that in Africa and other parts of the world. The prevalence of underweight and stunting in South Asia has been recorded as 46 and 44%, respectively.³ Chronic malnutrition has been a persistent problem for young kids in Sub-Saharan Africa. An excessive percentage of those children fail to reach the everyday worldwide popular height for their age, this is, they may be stunted. In contrast, the percentage of children stunted in Southeast Asia decreased from 52 percent to 42% between 1990 and 2006. The variety of undernourished (low weight for age)people of every age in sub Saharan Africa accelerated from about 90 million in 1970 to 225 million in 2008, and became projected to add some other 100 million by 2015, even earlier than the present day international food rate hikes.

A study conducted on influence of socio-economic factors on nutritional status of children in a rural community of Osun state, Nigeria revealed that 9 the prevalence rates of underweight, wasting and stunting were 23.1%, 9% and 26.7% respectively and also prevalence and determinants of malnutrition among Under-five Children of Farming Households in Kwara State, Nigeria results indicate that 23.6%, 22% and 14.2% of the sample children have been stunted, underweight and wasted, respectively.⁵

Nowadays, nearly one in three persons globally suffers from at least one form of malnutrition: wasting, stunting, vitamin and mineral deficiency, overweight or obesity and diet-related NCDs(Non communicable diseases). In 2014, about 462 million adults worldwide have been underweight, at the equal time 1.9 billion had been either overweight or obese.⁶ In 2016, an estimated 41 million children under the age of 5 years were overweight or obese, while 155 million were chronically undernourished.⁷ Nutrition-related factors contribute to approximately 45% of deaths in children aged under 5 years (mainly due to undernutrition), while low- and middle-income countries are now witnessing a simultaneous rise in childhood overweight and obesity.⁸ A study done on malnutrition among under-five children in Bangladesh revealed that the high prevalence of stunting and underweight, for instance, 42% and 40% of under-five children were stunted and underweighted, respectively.⁹ Also study conducted nutritional status of under- five children in Mongolia also showed that the prevalence of stunting, wasting and underweight were 15.6%, 1.7% and 4.7%, respectively.

In Ethiopia, malnutrition is a major contributor to under-five mortality. According to the 2016 Ethiopia Demographic and Health Survey report, 12% of under-five children had a diarrheal episode inside the 2 weeks before the survey.¹⁰ More than half of under-five child deaths are resulting from illnesses that are without difficulty preventable and treatable via simple, value-effective, and less costly interventions. Strengthening fitness systems to offer such interventions to all kids will probably save many children’s lives

The problem

 Malnutrition continues to be a main public health problem in developing countries. In Ethiopia, morbidity reports and community based studies have shown that malnutrition is a major public health problem that causes excess morbidity and mortality in children.¹⁰ In Ethiopia, infant malnutrition is one of the most critical public problems and the highest in the world.¹¹ The overall prevalence of underweight among children in Ethiopia was 25%.¹² In addition to this nutritional status of children in Ethiopia were not such much studied using Bayesian generalized additive models since it is the new field.

The foremost objective of this article is to identify predictors of children’s nutritional status in Ethiopia using the Bayesian generalized additive model. Specifically, we try to analyze the effect of continuous and categorical variables on nutritional status using the Bayesian generalized additive model. The reason why we want to use a generalized additive model: interpretability, flexibility/automation, and regularization. Hence, when our model contains nonlinear effects, GAM provides a regularized and interpretable solution while other methods generally lack at least one of these three features. In other words, GAMs strikes a nice balance between the interpretable, yet biased, linear model, and the extremely flexible, "black box" learning algorithms. In this case, some variables like Child Age (Childage), Age of Mothers at first Birth (AMB), Birth Order (BOD), Succeeding Birth Interval (SBI) and number of household member (Nhme) have a nonlinear effect on the response variables (i.e., weight for age and body mass index). For example, as we have seen from Figure 1, a number of household members (Nhme) has a nonlinear effect on the weight for age and which is difficult to interpret. So, smoothing is required to overcome this problem, which in turn included in the theory of generalized additive model as discussed above.

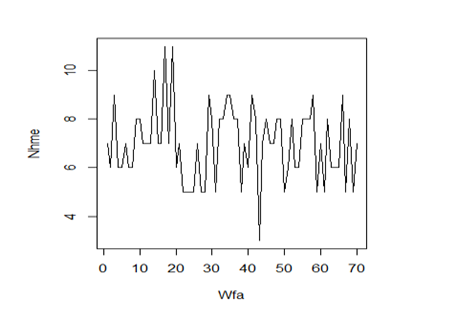
Figure 1 Relationship between number of household member (Nhme) as a nonlinear effect on the weight for age.

The output of this analysis will provide useful information on determinants of predictors of children’s nutritional status in Ethiopia, as well as concerned bodies, can take measurements on it.

Overview of burden child nutritional status

 Child as well as infant mortality remains higher in developing despite a considerable decline in mortality levels in the last decades. According to the latest State of the World Children Report, approximately 26,000 children are dying each day around the world mostly from preventable causes and one third of these deaths occur in the first month of life. Nearly all of these deaths occur in 60 developing countries. Moreover, nearly half of the under-five deaths are due to under-nutrition. Sub-Saharan Africa is the region worst hit by higher under-five mortality followed by South Asia. Similarly, under-nutrition remains to be a grave public health problem in the developing world with South Asia having the most affected region followed by Sub-Saharan Africa.¹³ Chronic malnutrition has been a chronic problem for children in sub-Saharan Africa. A high percentage of these children fail to reach the normal international standard height for their age that is they are the "stunted". In assessment, the percentage of children stunted in Southeast Asia dropped from 53 percent to 42 percent between 1990 and 2006. The range of undernourished (low weight for age) people of every age in sub-Saharan Africa elevated from about 90 million in 1970 to 225 million in 2008 and was projected to add every other one hundred million by 2015, even earlier than the present-day world food price hikes.¹²

Childhood under-nutrition is amongst the most serious health issues facing developing countries It is an intrinsic indicator of well-being, however, it’s also related to morbidity, mortality, impaired youth development, and reduced exertions productiveness. Much of the burden of deaths resulting from malnutrition, estimated to be over half of childhood deaths in developing countries, can be attributed to just mild and moderate under-nutrition. Underweight children are particularly vulnerable to increased risk of death from infectious illnesses such as diarrhea and pneumonia.¹⁴ For those children that do not survive, the impact of chronic malnutrition in the first few years of life are long lasting and can lead to cognitive and physical developmental deficits, higher levels of chronic illness and disability in adult life (resulting in reduced work capacity), as well as adverse pregnancy outcomes (low birth).

Factors associated with Children’s Malnutrition

 Important determinants of undernutrition include the education, income, and nutritional situation of the parents, access to clean water and sanitation, and access to primary health care and sex and age of child.^15,16 Factors that are contributing to malnutrition may differ among regions, communities and over time. Identifying the underlying causes of malnutrition in a particular locality is important to solve the nutritional problems. Approximately 10 percent of children born in Ethiopia die before their first birthday and 17 percent will die before their fifth birthday.¹⁰ According to formulas developed by 57 percent Of under-five mortality in Ethiopia is related to intense and severe to moderate malnutrition.¹⁷ The consequences of malnutrition in children additionally consist of bad physical development and confined intellectual talents that diminish their running capability during maturity. Some of the socioeconomic and demographic elements explaining child nutrition in line with studies done in different places are reviewed follows.

Education of mother: Education of women is believed to exert an impact on health and nutritional status of children since it provides the mother with the necessary skills for child care, increase awareness of nutritional needs and preference of modern health facilities as well as change of traditional beliefs about diseases causation, and use of contraceptives for birth spacing. Studies in Ethiopia,^15,16 indicate that the relationship between chronic nutritional status of children and maternal education.

Source of water and availability of toilet facility: Unfavorable health environment because of inadequate water and sanitation can boom the chance of infectious illnesses and circuitously motive sure forms of malnutrition. A com- parative study in some developing countries and in Jimma, Ethiopia¹⁸ showed that unprotected water source and non-availability of latrine were associated with low child stature.

Age of child: A cumulative indicator of growth retardation (height-for-age) in children is positively associated with age. Local studies in Ethiopia have also shown an increase in malnutrition with increase in age of the child.¹⁵ Children in the age group 0-5 months were found to be at significantly lower risk of stunting as compared with children in the age group 6-11 months.¹⁷ The prevalence of diseases and stunting rises with age.¹⁹

Gender of Child: In sub-Saharan Africa, male children under five years of age are more likely to become stunted than females.²⁰ A number of studies in Africa suggest that rates of malnutrition among.²¹

Birth Order: It is expected that parents give less attention to older children when a new child is born because the new born needs much attention and care. One study showed that stunting is rare in birth orders 2-3 and higher birth order (5+) is positively associated with child malnutrition. The risk of stunting was also 1.3 times higher for children of first birth order as compared with children of birth order six or more.²²

Birth interval of the child: Closely spaced pregnancies are often associated with the mother having little time to regain lost fat and nutrient stores.²³  Studies in developing countries showed that children born after a short birth interval (less than 24 months) have better tiers of stunting in maximum countries in which DHS surveys were conducted. It was also observed that as the preceding birth interval of the child decreases, the likelihood of being stunted increases.²²

Environmental factor: The impact of access to basic environmental services, such as water and sanitation on the probability children are stunted and underweight is examined in detail in Ethiopia and found as very significant.²⁴

The dData

This analysis is based on the 2011 Demographic and Health Survey (EDHS) data, which obtained from the Central Statistics Agency of Ethiopia. The 2011 EDHS sample was selected using a stratified; two-stage cluster design and census enumeration areas (EAs) were the sample units for the first stage. The sample included 62 EAs, 187 in urban areas and 37 in rural areas. Households comprised the second stage of sampling. An entire list of households was performed in each of the 624 selected EAs. A total of approximately 11,654 children under the age of 60 months were identified in over 17 thousand households of the selected clusters and then anthropometric measurements such as height, weight, and ages were made. In this analysis, we consider social-demographic and socioeconomic variables as independent variables, while body mass index and weight-for-age were taken as the dependent variables.

The model

 In this study, the authors used the Bayesian approach to predict the nutritional status of children. There have been tons of latest hobby in Bayesian inference for generalized additive and associated models. It is a method of statistical inference that allows one to combine prior information about a population parameter with the information contained in a sample.

Bayesian generalized additive regression model

Generalized Additive Model (GAM) is a method developed and popularized by Hastie, 2000.²⁵ It provides a powerful class of models for modelling nonlinear effects of continuous covariates in regression models. Generalized additive models extend traditional linear models in another way, namely by allowing for a link between $f\left(X_1,X_2,X_3,\mathrm{...},X_n\right)$ and the expected value of  as (Gelman, et. al.,²⁶ Bolstad;²⁷).

$E\left(Y\right)=f_0+f_1\left(X_1\right)+f_2\left(X_2\right)+\mathrm{...}+f_p{X}_p$       (1)

Where $f_i\left(X_i\right), i=1,2,\mathrm{....},p$ are smooth functions. These functions are not given a parametric form but instead are estimated by nonparametric methods. Generalized additive models consist of a random component, an additive component, and a link function relating these two components. It assume that, the response Y, the random component, has density in the exponential family.²²

$f(y_i|X_i)=exp\left(\frac{y_i{\theta }_i-b\left({\theta }_i\right)}{\varphi }\right)+c\left(y_i,{\theta }_i\right), i=1,\mathrm{...},n$       (2)

 Where:- 

• ${\theta }_i$ is the natural parameter of the exponential family,
• $\varphi$ is a scale or dispersion parameter common to all observations,
• $b(.)$ and $c(.)$ are functions depending on the specific exponential family.

 Moreover, the conditional expectation $E(y_i|X_i)={\mu }_i$ and with link function $g(.)$ we have ${\eta }_i=g\left({\mu }_i\right)$ . Where $X_i$  is the design matrix, g is the link function. The quantity $\eta$ in the generalized additive models can be expressed as.²⁸ i.e $\eta =f_0+{\displaystyle \sum }_{i=1}^p{f}_i\left(X_i\right)$ . Where, $f_1(.),\mathrm{...},f_p(.)$ are smooth functions that define the additive component. Finally, the relationship between the mean $\mu$ of the response variable and $\eta$ is defined by a link function.

Generalized additive models focus on exploring data none parametrically. It is more suitable for exploring the data set and visualizing the relationship between the dependent variable and the independent variables.²⁹

The smooth functions are typically represented in terms of linear combinations of smooth basis functions, for example, splines, and thus, can be added as columns to the model matrix. With a greater number of basis terms, more complex variations of the dependent variable can be described up to the limit of having the predicted curve pass through every point. Such a curve that describes the trend as well as the noise in the data will, in general, be poor at describing new samples from the same population. To control for this, a penalty for under smoothing is introduced during the optimization. The penalty is usually implemented as a proportion, λ of the integrated square of the second derivative of f (related to its curvature). Larger contributions of the term result in less smooth models ^30,31. The choice of degree of penalization (or smoothness) is controlled by minimizing a criterion related to prediction error (i.e. fitting some of the data and calculating the error on the remaining portion) called generalized cross validation (GCV).

The cubic spline smoother imposes smoothness on $f\left(x\right)$ . We seek the function $f\left(x\right)$ that minimizes[21]:

$\sum {(y_i-f\left(x_i\right))}^2+\lambda {{\displaystyle \int }}^{\text{}}{f}^{\text{'}\text{'}}{(x)}^{2}dx$

Notice that $f^{″}{(x)}^2$  measures the wiggliness of the function $f$ : linear $f\text{'}s$ have $f^{″}{(x)}^2=0$ while nonlinear produce values bigger than zero. $\lambda$ is a non negative smoothing parameter that must be chosen by the data analyst. It governs the trade-off between the goodness of fit to the data and (as measured by ${{\displaystyle \sum }}^{\text{}}{(y_i-f\left(x_i\right))}^2$ and wiggliness of the function. Larger values of $\lambda$ force $f$ to be smoother.

For any value of $\lambda$ the solution to $\sum {(y_i-f\left(x_i\right))}^2+\lambda {{\displaystyle \int }}^{\text{}}{f}^{\text{'}\text{'}}{(x)}^{2}dx$ ²⁸ is a cubicspline, i.e, a piecewise cubic polynomial with pieces joined at the unique observed values of  in the data set. Fast and stable numerical procedures are available for computation of the fitted curve.

Bayesian approaches are currently either based on regression splines second order random walk with adaptive knot selection³² or on smoothness priors²⁵ and own work. Inference is based on Markov chain Monte Carlo inference techniques.^33–35

Prior distribution

In Bayesian inference, the unknown function $f_j$ , j =1,...,p , the fixed effects parameters $\gamma ={({\gamma }_1,\mathrm{...},{\gamma }_r)}^{\text{'}}$ as well as the variance parameter ${\tau }^2$  are considered as random variables and have to be supplemented by appropriate prior assumptions. In the absence of any prior knowledge we assume independent diffuse priors ${\gamma }_j\propto const$ , j=1,...,r for the parameters of fixed effects^27-30.

1. The general form of the priors

Suppose that $f={(f\left(1\right),\mathrm{...},f\left(n\right))}^{\text{'}}$ is the vector of corresponding function evaluations at observed values of x. Then, the general form of the prior for is $f$

$f|{\tau }^2\propto exp\left(-\frac{1}{2{\tau }^2}{f}^{\text{'}}{\rm K}f\right)$      (3)

 where, k  is a penalty matrix that penalizes too abrupt jumps between neighboring parameters. In most cases K will be rank deficient; therefore the prior for f would be improper. We choose an inverse gamma distribution with hyper-parameters We choose an inverse gamma distribution with hyperparamters a and b, i.e.

${\tau }^2\sim IG\left(a,b\right)$

with probability density function given by:    

$p\left({\tau }^2/a,b\right)={({\tau }^2)}^{-a-1}exp\left(\frac{b}{{\tau }^2}\right)$

Common choices for a  and b  are a =1  and b =0.005  (or b =0.0005 ). Alternatively, one may take a=b=0.001

2. Priors for fixed effects

As indicated above for the parameter vector of fixed effects we choose a diffuse prior ${\gamma }_j\propto const$ , j=1,...,r Another choice would be to work with a multivariate Gaussian distribution $\gamma \sim N\left({\gamma }_0,{\sigma }_{{\gamma }_0}\right)$ . In this study, diffuse priors will be used for the fixed effects.

3. Priors for continuous effects under linear setup

Priors for the unknown functions $f_1,\mathrm{...},f_p$  depend on the type of the covariates and on prior beliefs about the smoothness of $f_j$  . In the following we express the vector of function evaluations $f_j={(f_j\left(x_{1j}\right),\mathrm{...},f_j\left(x_{nj}\right))}^{\text{'}}$  of a function $f_j$  as the matrix product of a design matrix X_j and a vector of unknown parameters ${\beta }_j$  s’, i.e

$f_j=X_j^{\text{'}}{\beta }_j$

4. First and second order random walk priors

Let us consider the case of a continuous covariate X with equally spaced observations $x_i$  , i = 1,..., m, $m\le n$ , then, $x_{\left(1\right)}<\mathrm{...}<x_{\left(m\right)}$  defines the ordered sequence of distinct covariate values. Here m denotes the number of different observations for X in the data set. A common approach in dynamic or state space models is to estimate one parameter $f\left(t\right)$ $x\left(t\right)$  for each distinct $x\left(t\right)$  ; i.e., define, $f\left(t\right)=f\left(x_{\left(t\right)}\right)$  and let $f={(f\left(1\right),\mathrm{......},f\left(m\right))}^{\text{'}}$  denote the vector of function evaluation. Then a first order random walk prior for  is defined by:

$f\left(t\right)=f\left(t-1\right)+u\left(t\right)$       (4)

 A second order random walk is given by

$f\left(t\right)=2f\left(t-1\right)-f\left(t-2\right)+u\left(t\right)$       (5)

with Gaussian errors $u\left(t\right)\sim N\left(0,{\tau }^2\right)$ and diffuse priors $f\left(1\right)\propto const$ and $f\left(2\right)\propto const$ , for initial values, respectively.

5. Bayesian P-splines

Any smoother depends heavily on the choice of smoothing parameter, and for P spline in a mixed (fixed and continuous) framework. A closely related approach for continuous covariates is based on the P-splines approach introduced by Eilers and Marx (1996). The basic assumption of this approach is that the unknown function $f_j$  can be approximated by a spline of degree l with equally spaced knots $x_{min}={\xi }_0<{\xi }_1<\mathrm{...}<{\xi }_{r-1}<{\xi }_r=x_{max}$  within the domain of $x_j$ .

Posterior Inference

When performing Bayesian inference, all inferential conclusions are based on the posterior of the model. In an empirical Bayes approach to structured additive regression, no hyper-prior are assigned to the hyper-parameters, i.e. the variances ${\tau }_j^2$  are treated as fixed. In this case, the specific form of the posterior depends only on the parameterization of the regression terms in the model. Then, we use Markov Chain Monte Carlo (MCMC) simulations to draw samples from the posterior and statistical inference is done by means of Markov Chain Monte Carlo techniques in a full Bayesian setting. Now we restrict the presentation to models with predictor. Full Bayesian inference is based on the entire posterior distribution. Let be the vector of all unknown parameters, then the posterior is given by.

$\begin{array}{l}p\left(\alpha /y\right)\propto L\left(y,{\beta }_1,{\tau }_1,{\beta }_2,{\tau }_2,\mathrm{...},{\beta }_{\pi },{\tau }_{\pi },\gamma \right){\displaystyle \prod }_{\phi =1}^{p}p\left({\beta }_{j/{\tau }_j^2}p\left({\tau }_j^2\right)\right)\\ \propto L\left(y,{\beta }_1,{\tau }_1,{\beta }_2,{\tau }_2,\mathrm{...},{\beta }_p,{\tau }_p,\gamma \right)\end{array}$

${\displaystyle \prod }_{j=1}^p{(\frac{1}{{({\tau }_j^2)}^{k\left(\frac{k_j}{2}\right)}}exp\left(-\frac{1}{2{\tau }_j^2}\right){\beta }_j^{\text{'}}{K}_j{\beta }_j{\displaystyle \prod }_{j=1}^p{\tau }_j^2)}^{-a_j-1}exp\left(-\frac{b_j}{{\tau }_j^2}\right)$

In a fully Bayesian approach, parameter estimates are generated by drawing random samples from the posterior via MCMC simulation techniques. The variance parameters ${\tau }_j^2$ can be estimated simultaneously with the regression coefficients ${\gamma }_j$ by assigning additional hyper-prior to them. The most common assumption is, that the ${\tau }_j^2$ are independently inverse gamma distributed, i.e. ${\tau }_j^2\propto IG\left(a_j,b_j\right)$ , with hyper-parameters $a_j$  and $b_j$  specified a prior. A standard choice is to use $a_j=b_j=0.001$ .^36,32

Model Diagnostic

Once a model has been developed, we now would like to know how effective the model is in describing the outcome. This is referred to as goodness of fit. The most common ways of checking goodness of fit are: diagnosis for convergence and mixing and posterior-predictive check. In this study, Time series plots were used.³⁷

Comparison of the model

 There are several methods of model selection. In this analysis, AIC (Akaike information criterion), DIC (Deviance information criterion) and GCV (Generalized cross validation) are used to compare the linear frequent and the linear Bayesian approach. The model with the smallest AIC, DIC and GCV value considered a better fit.³¹

Overall procedures

The authors estimated a model parameters that mainly focuses on factors that are underlying determinants of nutritional status of children. And apply Generalized linear additive model to investigate linear and non-linear effects of covariates more flexibly than most previous works.

Descriptive analysis of the data

The result displayed on Table 1 shows the percentages and counts of underweight status of children with respect to the categorical explanatory variables. As one can see from Table 1, among the  cases examined in this study  of male children were underweight and  of female children were underweight. The highest prevalence of child malnutrition was observed among children whose preceding birth interval was less than 24 months () unlike to the lowest prevalence of child malnutrition which was recorded from children whose preceding birth interval is 48 and above (31.9%).

The proportion of underweight children as we can seen from Table 1, it is also differs by type of place of residence: urban and rural. Accordingly, higher numbers of underweight children (33.6%)) reside in rural areas, and relatively less numbers of underweight children (31.2%) reside in urban centers.

The evidence given in Table 1 shows that the percentage nutritional statuses of children who had diarrhea recently seem to be high probability of underweight than those children which had no diarrhea recently.

Likewise, one can observe that the percentages nutritional status of children who had fever recently seemed high probability of underweight than those children who have no fever recent (33.9%, 33.1%, respectively).

The evidence given in Table 1 shows that the percentages nutritional status of children in households who had used other water sources seemed to be more underweight than those children in households which used water from public source.

The family education level has also it’s effect on the nutritional status of children that a mother with higher educational level(father education level) had a child with better nutritional status. Since the percentages of underweight is decreasing from no education to secondary and above education level. Children who had disease are affected by malnutrition e.g child who had cough is more affected than child who had not cough as we observe from Table 1.

From Table 2 the highest malnourished region are SNNP, Oromia, Gambela, Affar and Tigray. From all of these region the smallest malnourished region is Harari. The place of residence has also its impact as result the highest malnourished lives in rural comparing with urban.

Inferential part

 Under this, we use Gaussian linear regression model to analyze the determinants that have linear effects and Gaussian additive model on its part which can be used to analyze variables that have a non linear effects. The semi parametric regression model that includes the linear effects categorical coariates as well as the non linear of continuous variables.

Bayesian generalized additive regression model: Under this we use Gaussian additive model which can be used to analyse variables that have a non-linear effect. In this case, the main interest is to model the dependence of weight for age of under five years old children and body mass index on continuous covariates including child’s age in month (Childage), Age of mother at first birth(AMB), birth order(BOD), succeeding birth interval(SBI) and Number of household member(Nhme).

Based on above concept, for these continuous covariates in the data set, the assumption of a strictly linear effect on the response y may not be appropriate. Generally, it will be difficult to model the possibly nonlinear effect of such covariates through a parametric functional form, which has to be linear in the parameters, prior to any data analysis. To overcome these difficulties, we replace the strictly linear predictor through an additive predictor, leading to the additive regression model.

The first thing to note is, from Table 3 and Table 4 the output is separated into parametric and smooth, or nonparametric parts. In this additive Gaussian regression model, from Table 3 of the parametric component, succeeding birth interval, sex of child, children by choice not by chance, ever had vaccination and had cough recently are significant affect on underweight status of children under age five years. The variables like duration of beast feeding, source of drinking water and number of household member(Nhme) are significant at  level and can effect weight for age of child.

The GCV, or generalized cross validation score can be taken as an estimate of the mean square prediction error based on a leave-one-out cross validation estimation process. However, the GCV score is an efficient measure of this concept that doesn’t actually require fitting all those models and overcomes other issues. The GCV, doesn’t give as what we require since its value is largest.

From Table 4 results child’s age in month, number of household member and succeeding birth interval significant at 10% and significant respectively, and affect weight for age of child. From Table 4 if the effective degrees of freedom for the smooth term is high and we observe that p-value is small or become significant and vice versa. So the corresponding variables become important affect on the response variables.

From Table 5 and 6 had cough, sex of child and children by choice not chance are significant and ever had vaccination and duration of breast feeding are significant at 10% level. And affect body mass index. Child’s age in month, succeeding birth interval and number of household member and are significant at 10% level. And affect body mass index of child.

From Figure 2 Diagnostic Plots for the Generalized Additive Model 

1. A theoritical quantile-comparison plot of the residuals allows us to look for outliers and heavy tails.
2. Residuals versus linear predictors (simply observed y for continuous variables) helps detect non constant error variance.
3. Histogram of the residuals are good for detecting non normality.

Figure 2 Diagnostic plots for the generalized additive model.

Here we can see the negative, positive and constant slight effect of the continuous variables on child nutritional status. From Figure 3 of Childage (months) versus s(Childage) shows the relationship between Childage and Wfa (weight for age) holding constant the BOD (Birth order), SBI (Succeeding birth interval), Nhme (Number of household member)and AMB (Age of mother’s at first birth) variables in the model. And, this interpretation is the same as true for the variables BOD (Birth order), SBI (Succeeding birth interval), Nhme (Number of household member)and AMB (Age of mother’s at first birth).

Figure 3 Non-linear effects of continuous variables.

Since Wfa (weight for age) is expressed in mean deviation form, the smooth term s(Childage), s(AMB), s(BOD), s(SBI) and s(Nhme)are also centered and thus each plot represents how Wfa (weight for age) changes relative to its mean with changes in Childage, AMB, BOD, SBI, and Nhme respectively.

One can observe that from Figure 3 the influence of a child’s age on its nutritional status is considerably high in the age range between the ages of 0-26 months with decreasing trend; and then stabilizes.   

As suggested by the nutritional literature, one can able to distinguish the continuous worsening of the nutritional status up until about 26 months of age. This deterioration set in right after birth and continues, more or less linearly, until 26 months. After 42 months the effect of age on underweight stabilizes at a low level. Through reduced growth and the waning impact of infections, children were apparently able to reach a low-level equilibrium that allows their nutritional status to stabilize.

It is also evident from Figure 3 we analyze that underweight status of children is some what stable until 21 years for age of mother at first birth and after 21 it becomes slightly increase. That is younger mothers tend to have stable underweighted children than older mothers.

As we can see in Table 8, $\lambda$ is a non negative smoothing parameter that must be chosen by the data analyst. It governs the trade off between the goodness of fit to the data and the wiggleness of the function. When goes to infinity, the penalty term becomes more important, forcing $f^{″}\left(x\right)=0,$  thus the result is the least square line. While when $\lambda$ goes to zero, the penality becomes unimportant, thus a solution is the second derivative function. The larger value of $\lambda$ (Table 13, sx(Childage)=7500.000) produce smoother curves while the smallest values (Table, sx(Nhme)=10.924) produces more wiggly curve than the others.

In fact degree of freedom of smoother is inconvenient to express the desired smoothness of functions in terms of $\lambda$ . Degree of freedom of a smoother, sometimes called effective number of parameters, is an indication of the amount of smoothing. The smoothing parameter is the major determinant of the degree of freedom. More smoothing means fewer degree of freedom (Table 8, sx(Childage)=1.9720) or higher span. The degree of freedom is not necessary an integer. The higher value of $\lambda$ means lower value of degree of freedom and vise versa (Table 8).

From Table 9 sex of child, children by choice not by chance and ever had vaccination are significant. This can be seen as body mass index of female children is lowered by  compared to male children. In similar way, body mass index of child who had ever vaccinated is lowered by  comparing to not vaccinated, which indicate only vaccination is not enough for child.

The model in Bayesian approach for Bayesian generalized additive model for MCMC post estimation diagnosis, it is also possible to extract sampling paths of parameters with function samples or to plot the samples directly. For instance, coefficient sampling paths for term sx(SBI) are displayed which is important to check the model convergence so as we observe from Figure 4.

Figure 4 Checking for the convergence posterior distribution by time series plot.

Model comparison

We analysed the DHS data set using four different approaches. It is reasonable to ask which type of model is better. The four models are listed in the following: Model 1 = Generalized additive model in frequentist Model 2 = Generalized additive model in Bayesian Model selection is an important part of statistical analysis, and indeed is a central to the pursuit of science in general. Many authors have examined this question, from both frequentist and Bayesian perspective, and many tools of selecting the "better model".

The models proposed in this study are quite general and the model building process can be quite challenging. Currently, an automated procedure for Bayesian model selection is not available. However, a few recommendations are possible. 1. Users should try to incorporate everything that is theoretically possible. 2. Different Bayesian models could be compared via the DIC.³⁸ 

1. Users should try to incorporate everything that is theoretically possible.
2. Different Bayesian models could be compared via the DIC.³⁹

From Table 11, When we compare models 1 model 2, from Table 11 by GCV we easily see that models 2 have less GCV values, which means Bayesian Generalized additive models are clearly much better than models 1 (Generalized additive model in frequentist). Since, models 2(Generalized Additive model in Bayesian) has less GCV values (2188290) and (2142190) than models 1 (2.2178e+6) and (2.1717e+06) respectively.

Discussion

 This study was intended to identify the determinants of the weight for age and body mass index of nutritional status of children under five years old in Ethiopia based on EDHS 2016 data. The nutritional status was measured by the weight-for-age and body mass index is measured by weight/height.

In the study, the effect of the age of the child is obviously nonlinear and decreasing between birth and an age of about 30 months and then stabilizes. That means the underweight of children increases until 30 months. This continuous worsening of the nutritional status may be caused by the fact that most of the children obtain liquids other than breast milk already shortly after birth. After 30 months a relatively stable, low level is reached. However, it reaches its minimum level between ages 40-50 months, then rises again and stabilizes thereafter at a middle level with a bump till 5 years. Previous studies also conform this (RE Black, 2013,³⁹ Mohammad, 2018,⁴⁰)

In the study, the effect of the age of the child is obviously nonlinear and decreasing between birth and an age of about 26 months and then stabilizes. That means the underweight of children increases until 26 months. This continuous worsening of the nutritional status may be caused by the fact that most of the children obtain liquids other than breast milk already shortly after birth. Between 30-40 months a relatively decreases and 41-50 months become stable, low level is reached. However, it reaches its minimum level between ages 30-50 months, then rises again thereafter at a middle level with a bump till 5 years. Previous studies also conform this (Mohammad, 2018,⁴⁰Loader, 1999.⁴¹)

Conclusions

The results found that children living in the Afar and Oromia region of Ethiopia are associated with weight for age (underweight). While the children which are living in Harari and Somali are less associated with underweight comparing with other regions.

Determinants that affect levels of nutritional status of children have been explored using different models like generalized additive model in frequentest and Bayesian approach. By using model comparison methods, surprisingly generalized additive model in Bayesian approaches is the preferable one.

The analyses shows that child sex, children by choice not by chance, vaccination, source of drinking water, duration of breast feeding and cough important fixed factors which affect the weight for age of children in Ethiopia. Variables like succeeding birth interval, child gender, children by choice not by chance, vaccination, and cough are also affect body mass index.

Concerning the non-linear effects, a major finding is that the malnutrition status worsens until 26 months of age of their life and between 30-40 and 41-50 months become decrease and stable respectively and again increase. The effect of AMB (Age mothers at first birth) is slight on childhood malnutrition until 22 months but effect of underweight seems increase above 22 months. In contrast the effects of succeeding birth interval on underweight are also increase above 45 months and slightly change/fluctuate below 45 months.

Mother education level, which is related to wealth index, is a determinant of good child care knowledge and practices. In this study, the education attainment of mothers does not have a significant effect on the underweight of a child in Ethiopia in separate analysis. This result is against the suggestion that an educated mother assumes the responsibility of taking a sick child to receive care health. Mother education level, which is related to succeeding birth interval have also determine the body mass index since they are significant effect.

Recommendations

 In addition to the efforts being made to reduce malnutrition in general, specific attention should be given to reduce the prevalence of malnutrition by taking the following in to consideration. The concerned body: 

• Should give due attention to the high-risk factors identified as contributing high risk of malnutrition in children under five years of age due emphasis.
• Should be given better source of water for community in more facilitated manner.
• Since children less than 26 months and above 50 months of their life were highly and slightly prevalent to malnutrition respectively, as analysis of this study showed, they should be given special care like giving vaccination and support as much as possible.
• And also male and female children should be equally treated and have similar care and support since female children were more likely to be underweight than male children in Ethiopia.
• Finally, further findings should be incorporating for additional risk factors which are associated with childhood malnutrition in Ethiopia regional wise.
• In generalized additive model, to handle the effect of continues covariate on response variables we apply the concept of P-spline as well as smoothing and we obtained the approaches of the required results. Concerned body can modify to obtain more required (more approached) results.

Limitations of the study

 Spatial information can be analyzed in Bayesian approach and result in very important information to identify the prevalence of stunting region-wise and/or district-wise. Because of lack of having complete spatial information, in this study we have not analyzed the prevalence of child malnutrition in-depth spatially.

The data, we used in this study is EDHS 2011. The researcher find any option to get recent data. Since latest data is not released till now and we haven’t any option to do more. The only option we have is only doing on the EDHS 2011 data. Thus, the results may not necessarily reflect the current situation of Child’s nutritional status of children.

Under this study the regional differences are not considered either we observe which regional has highest prevalence of underweight or low prevalence of underweight.

1. The state of the World’s children; a unicef report, Childhood Under Threat. 2015.
2. Caulfield LE, de Onis M, Blssner M, et al. Undernutrition as an underlying cause of child deaths associated with diarrhea, pneumonia, malaria, and measles. Am J Clin Nutr. 2014;80(1):193–198.
3. De Onis M, Frongillo EA, Blssner M. Is Malnutrition declining? an analysis of changes in levels of child malnutrition since 1980. Bull World Health Organ. 2000;78(10):1222–1233.
4. AArmstrong J, Dorosty AR, Reilly JJ, et al, Child health information team. coexistence of social inequalities in undernutrition and obesity in preschool children, population based cross sectional study. Arch Dis Child. 2003;88:671-675.
5. Senbanjo IO, Adeodu OO, Adejuyigbe EA. Influence of socioeconomic factors on nutritional status of children in a rural community of osun state, Nigeria. 2009.
6. NCD risk factor collaboration. Trends in adult body-mass index in 200 countries from 1975 to 2014: a pooled analysis of 1698 population-based measurement studies with 19·2 million participants. Lancet. 2016;387(10026):1377–1396.
7. USAID. Nutritional status and its determinants in southern Sudan. 2017.
8. World health organization. Global health observatory (GHO) data. Under-five mortality. 2015.
9. Siddiqi NA, Haque N, Goni MA (2011); Malnutrition of Under-Five Children: Evidence from Bangladesh; Asian Journal of Medical Sciences 2, 113-118.
10. Central Statistical Agency: Ethiopia Demographic and Health Survey. 2016.
11. Alemu M, Nicola J, Belele T. Tackling child malnutrition in Ethiopia, young lives. Project Working Paper No 19. Save the Children UK. 2015:26.
12. Central intelligence agency. The World Fact Book: Ethiopia. 2014.
13. United nations childrens fund. Tracking progress on child and maternal nutrition, a survival and development priority, UNICEF, New York. 2009.
14. Kwena AM, Terlouw DJ, de Vlas SJ, et al. Prevalence and severity of malnutrition in pre-school children in a rural area of Western Kenya. Am J Trop Med Hyg. 2003;68:94–99.
15. Yimer G. Malnutrition among children in southern Ethiopia, levels and risk factors. Ethiopian Journal of Health Development. 2000;14:283-292.
16. Dejen A. The determinants of nutritional status of children in Ethiopia using Multivariate analysis. MSc thesis in applied statistics. AAU; 2008.
17. Girma W, Timotiows G. Determinants of the nutritional status of mothers and children in Ethiopia. USA: ORC Macro; 2002.
18. Getachew A, Guadu T, Tadie A, et al. Diarrhea prevalence and sociodemographic factors among under-five children in rural areas of North Gondar Zone, Northwest Ethiopia. Int J Pediatr. 2018.
19. World Health Organization. Global strategy for infant and young child feeding. Geneva: United Nations Children Fund; 2006.
20. Hanieh S, Ha T, Simpson J, et al. Exclusive breast feeding in early infancy reduces the risk of inpatient admission for diarrhea and suspected pneumonia in rural Vietnam: a prospective cohort study. BMC Public Health. 2015;15(1):1166.
21. Christiansen L, Alderman H. Child malnutrition in Ethiopia: can maternal knowledge augment the role of income? World Bank; 2001.
22. Otgonjargal D, Bradley A, Woodruff F, et al. Nutritional status of under five children in Mongolia. Journal of Medicine and Medical Sciences. 2012;3(5):341–349.
23. Janet C King. The risk of maternal nutritional depletion and poor outcomes increases in early or closely spaced pregnancies, The Journal of Nutrition. 2003;133(5):1732S–1736S.
24. Liz Comrie-Thomson, Jess Davis, Andre Renzaho, et al. Published by the office of development electiveness, Australian government department of foreign affairs and trade, Canberra. 2014
25. Hastie T, Tibshirani R. Generalized Additive Models. London: Chapman and Hall; 1990,2000.
26. Gelman A, Carlin JB, Stern HS, Dunson D, et al. Bayesian Data Analysis, third ed. London: Chapman & Hall; 2013.
27. Bolstad William M. Understanding Computational Bayesian Statistics. John Wiley; 2010.
28. Green PJ. Reversible-jump markov chain monte carlo compu-tation and bayesian model determination. Biometrika. 1995;82(4):711732.
29. Stramer, O.; Tweedie, R. (1999). "Langevin-Type Models II: Self-Targeting Candidates for MCMC Algorithms". Methodology and Computing in Applied Probability. 1 (3): 307–328. doi:10.1023/A:1010090512027.
30. Rubinstein RY, Kroese DP. Simulation and the Monte Carlo Method. 2nd ed. Wiley; 2007.
31. Robert CP, Casella G. Monte Carlo Statistical Methods. 2nd ed. Springer-Verlag; 2004.
32. Edris M. Assessment of Nutritional Status of Preschool Children of Gumbrit. Ethiopia J Health Dev. 2006;21;125−129.
33. Asmussen Sren, Glynn Peter W. Stochastic simulation: algorithms and analysis. Stochastic Modelling and Applied Probability. 2007.
34. Liu JS, Liang F, Wong WH. The multiple-try method and local optimization in metropolis sampling. Journal of the American Statisti-cal Association. 2000;95(449):121134.
35. Casella, G.; George, E. I. (1992). "Explaining the Gibbs Sampler". The American Statistician. 46 (3): 167. doi:10.2307/2685208. JSTOR 2685208.
36. Levin David A, Peres Yuval, Wilmer Elizabeth L. Markov Chains and Mixing Times. American Mathematical Society. 2008.
37. Green PJ. Reversible-jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika. 1995;82(4):711−732.
38. Spiegelhalter D., Best N., Carlin B., and Van der Line A. (2002); Bayesian Measures of Models Complexity, Journal of the Royal Stat. Soc,B(64), 1-34.
39. RE Black, CG Victora, SP Walker, et al. Maternal and child undernutrition and overweight in low-income and middle income Countries. Lancet. 2013;382(9890):427451.
40. Mohammed S, Asfaw ZG. Bayesian Gaussian regression analysis of malnutrition for children under five years of age in Ethiopia. EMDHS 2014. Archives of Public Health. 2018:1–11.
41. Loader C. Local regression and likelihood. New York: Springer; 1999.