
Research Article Volume 5 Issue 4
Hidden markov model approaches for biological studies
Xiang Yang Lou1,2
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

1Department of Pediatrics, University of Arkansas for Medical Sciences, USA
2Arkansas Children's Hospital Research Institute, USA
Correspondence: Xiang-Yang Lou, Ph.D., 1 Children?s Way, Slot 512-43, Little Rock, AR 72202, USA, Tel 1-501-364-6516, Fax 1-501-364-1413
Received: February 14, 2017 | Published: March 31, 2017
Citation: Lou XY. Hidden markov model approaches for biological studies. Biom Biostat Int J. 2017;5(4):132-144. DOI: 10.15406/bbij.2017.05.00139
Download PDF
Abstract
Organism is a multi-level and modularized complex system that is composed of numerous interwoven metabolic and regulatory networks. Functional associations and random evolutionary events in evolution result in elusive molecular, physiological, metabolic, and evolutionary relationships. It is a daunting challenge for biological studies to decipher the complex biological mechanisms and crack the codes of life. Hidden Markov models and more generally hidden Markov random fields can capture both random signals and inherent correlation structure typically in time and space, and have emerged as a powerful approach to solve many analytical problems in biology. This article will introduce the theory of hidden Markov model and the computational algorithms for the three fundamental statistical problems and summarize striking applications of hidden Markov models to biological and medical studies.
Keywords: hidden markov model, hidden markov random field, applications to biological studies, pattern recognition for biological sequence, genetic mapping, gene prediction, biological image analysis
Introduction
A Markov process, named after the Russian mathematician Andrey Andreyevich Markov who developed much of relevant statistical theory,M1 is a stochastic process that satisfies the Markov property characterized as "memorylessness" (also known as “non-aftereffect”).2 The term “stochastic process”, also called random function that is interpreted as a random element in a function space, refers to the statistical phenomenon that the outcomes of a collection of events or variables, typically in temporal and/or spatial order, are not deterministic, but, instead, probabilistic, and "memorylessness" means that given the state of a variable (or the states of a few adjacent variables) in a process, the succeeding variables and preceding variables are conditionally independent in the sense of probability. Markov processes can be categorized into various types according to the nature such as whether the parameter of random function is continuous or discrete and whether the state space is countable or infinite: discrete-time vs. continuous-time, countable vs. infinite states, first-order (the conditional probability of a variable depending only on its one preceding variable) vs. high-order (the conditional probability of a variable depending on its few preceding variables), time-homogeneous (stationary transitional probabilities) vs. time-nonhomogeneuous, and uni-dimensional vs. multi-dimensional. Markov processes are quite common in both the natural world and human societies; random walk, drunkard's walk, Lévy flight, Brownian motion, and the thermal electron transfer between different sites, are all examples of time-homogeneous continuous-time Markov processes;3 spread of epidemics, growth of populations, and vegetation dynamics can be approximated by a Markov process.4,5 Markov chain is a special type of Markov process countable in state space and discrete in time.6 In most cases of interest, the states in an underlying Markov process are not observable but there exists a probabilistic function of the states that can be associated with another set of stochastic sources that produce observed symbols, characterized as signals, correspondingly, called a hidden Markov process.7 The probabilistic model to characterize a hidden Markov process is referred to as a hidden Markov model (abbreviated as HMM). The most common HMM is uni-dimensional (one-dimensional), and extension to high-dimensional cases includes multi-dimensional hidden Markov model or Markov mesh random field, and more generally, Markov random field (MRF), also known as Markov network. There are a wide range of applications of HMMs to signal processing, speech recognition, character decoding, imaging analysis, economics, sociology, and life sciences.3,8-10 This review will briefly describe the statistical principle of HMMs and then focus on recent advances in applications of HMMs to biology and biomedicine.
Hidden markov model
The hidden Markov process is a class of doubly stochastic processes, characterized by Markov property and the output independence, in which an underlying Markov process is hidden, meaning the variable states cannot be directly observed, but can be inferred through another set of stochastic processes evident as a sequence of observed outputs.11 The Markov process generates the sequence of states of variables, specified by the initial state probabilities and state transition probabilities between variables, while the observation process outputs the measurable signals, specified by a state-dependent probability distribution, thus being viewed as a noisy realization of a Markov process. In what follows the first-order HMM is used to illustrate the theory. Since any probabilistic question about higher order Markov chains is reducible by a data augmentation device to a corresponding question about first Markov chains,6 extension of those methods to the higher order cases will be straightforward. As shown in Figure 1A, a uni-dimensional (1-D) hidden Markov process involves a sequence of hidden random variables
(
), where each variable
has
potential states, and of which the conditional probability satisfies the Markov dependence,
,
, namely, the underlying states follow a first-order Markov chain. If
(
), that is, the transitional probability is independent of the position of a variable in the sequence, it is called a time-homogeneous Markov chain. Without loss of generality, the time-nonhomogeneous Markov chain is used here to illustrate the statistical principle. There are a series of output signals either discrete or continuous, denoted by
, associated with the variable states underlying a hidden Markov process (
) that are not observed through a set of probability distributions. A hidden Markov process can be characterized by the corresponding HMM, which is formally defined by the following components: the elemental structure including the hidden variables and their state spaces, and the output symbols and their value ranges, and a set of three-tuple parameters denoted by
, where
is the initial state probability distribution,
is the state transition probability distribution, and
is the emission probability distribution. The initial probability vector is,
,
,
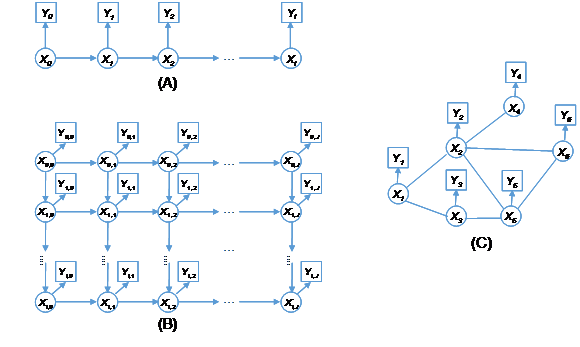
Figure 1 Hidden Markov processes: (A) One-dimensional hidden Markov process, (B) Two-dimensional hidden Markov process, and (C) Hidden Markov random field.
where
; the transition probability matrix of variable
(
) is,
,
,
,
where
; the output probability distribution of observation
(
) is, either a matrix or a family of distributions depending on the type of observations,
,
,
where
.
As shown in Figure 1B, the underlying process of a two-dimensional (2-D) hidden Markov process is a Markov mesh consisting of an array of random variables,12,13 where each variable
can potentially take
states (
,
), and of which the conditional probability of a node in the 2-D lattice satisfies the property of memorylessness, only depending on the nearest neighbors,
,
,
,
where
,
is the state transition probability, denoted by
; when
,
,
,
where
is the transition probability, denoted by
; when
,
,
,
where
is the transition probability, denoted by
; when
and
, there are a set of the initial state probability
, denoted by,
,
,
where
. The output signal
conforms to the following distribution, given the state of
, being conditionally independent of the states of the other variables and the other observations,
,
,
,
where
is the output probability, denoted by
.
HMM can be further extended to the higher dimensional cases,14-17 and even more generally as hidden MRFs or Markov networks.18-23 A hidden MRF is a Markov random field degraded by conditionally independent noise, of which the set of underlying variables are latent,24 often described by a graphical model for its representation of dependencies. As shown in Figure 1C, each vertex (node) corresponds to a variable and the edge connecting two vertices represents a dependency. When there is an edge to connect every two distinct variables in a subset of vertices, such a subset is called a clique. Each clique is associated with a set of nonnegative functions, called potential functions, to specify its probability distribution. A maximal clique is a clique that cannot be extended by including one more adjacent vertex, that is, a clique which does not exist exclusively within the vertex set of a larger clique. The joint distribution of a set of variables in a MRF can be expressed by a product of several potential functions based on clique factorization,
,
where
are a set of cliques, usually a set of maximal cliques,
is the potential functions of clique c,
is the states of clique c,
is the normalizing constant so that the sum of probabilities over the whole range equals to 1. The underlying variables are hidden but each variable will output a signal confounded with noise. The output observation of a variable is conditionally independent of the states of other variables and the other outputs.
Statistical inference in hidden markov models
Three fundamental problems are addressed for HMMs:11 (1) evaluation or scoring, to compute the probability of the observation sequence for a model, (2) decoding or optimization, to find the optimal corresponding state sequence given the observation sequence and the model, (3) learning or training, to estimate the model parameters (initial probabilities, transition probabilities, and emission probabilities) that best explains the observation sequences given the model structure describing the relationships between variables. Although all these computations can be implemented by the naive brute-force algorithms, which exhaustively enumerate all possible state sequences and do calculations over them for the observed series of events, they are not effective enough. The computational complexity of such algorithms increases exponentially with problem size, so that the implementation quickly becomes computationally infeasible as the number of states and the number of sequences increase, even for a small number. The 1-D Markov model can be used to illustrate this point. When moving from a variable to the next along the Markov chain, each current state may shift to one of the possible next states, and then a state transition diagram can be formed by connecting all plausible moves, as shown in Figure 2A. Each path from the first variable to the final variable represents a possible state combination, and there are a total of
paths, which can be, in many cases of interest, an astronomical number. Powerful algorithms can be developed through recursive factorization or dynamic programming by making use of the conditional independence given the Markov blanket of a variable or a group of variables, so that substantial redundant calculations and storage are avoided, and much fewer arithmetic operations and less computing resources such as computer memory are required.
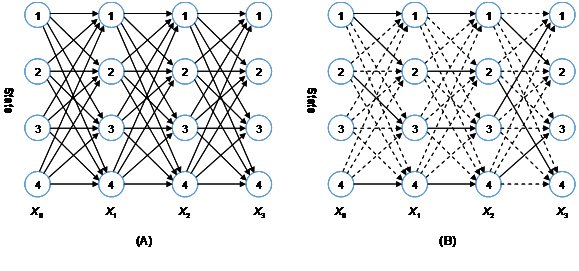
Figure 2 Trellis algorithm: (A) The forward trellis and (B) The Viterbi trellis.
The principle of trellis algorithm is extensively used in statistical analysis for 1-D hidden Markov models. As visualized in Figure 2, the states in various variables are arranged into a trellis according to the order of variables, whose dimensions are, respectively, the number of states and the length of the variable sequence. The nodes at a vertical slice represent the states of the corresponding variable. In a trellis graph, each node at each variable position connects to at least one node at the previous variable and/or at least one node at the next variable (each node for the first variable and at the last variable can be viewed to always connect with one dummy node before the start position and after the final position, respectively), then forming an interconnected network. By use of the conditional independency, the intermediate calculations on all the paths in which a node is involved can be individually cached to avoid redundant calculation. The forward-backward algorithm,25,26 the Viterbi algorithm,27-29 and the Baum-Welch algorithm (a special type of Expectation-Maximization, abbreviated by EM, algorithm),30,31 were developed based on the trellis diagram and can used for purposes of evaluation, decoding, and learning, respectively. The relevant theory and methods is concisely recapitulated as follows.
Forward-backward algorithm
The recursive forward or backward algorithm can be used to compute the probability of a sequence of observations (
,
,…,
) generated by a particular model, denoted by,
.
Corresponding to each node in a trellis diagram (Figure 2A), two storage variables are used to cache the forward probability (the sum of probabilities of all paths leaving from the start of the sequence and ending in the state considered) and the backward probability (the sum of probabilities of all paths starting with the considered state and going to the end of the sequence), respectively, denoted by
and
(
,
). Both the forward algorithm and the backward algorithm involve three steps: initialization, recursion (or induction), and termination.
(1) Initialization
Calculate the forward probability at the first position,
,
.
Specify the backward probability at the last position,
,
.
(2) Recursion
Compute the forward probability,
,
,
.
Compute the backward probability
,
,
.
(3) Termination
When
, the forward recursion stops. Then, the probability of the whole sequence of observations can be found by summing the forward probabilities over all the states at the final variable,
.
When
, the backward recursion stops. Then, the probability of the whole sequence of observations can also be found by summing the products of the forward and backward probabilities over all the states at the first variable,
.
Viterbi algorithm
The Viterbi algorithm can be used to identify the most likely sequence of hidden states to produce an observed sequence, termed the Viterbi path, denoted by
, so that,
.
Corresponding to each node (Figure 2B), two storage variables are used to cache the probability of the most likely path for the partial sequence of observations and the state at the previous variable to lead this path, denoted by
and
(
,
), respectively. The Viterbi algorithm consists of four steps: initialization, recursion, termination, and backtracking.
(1) Initialization
Calculate
and set
,
.
(2) Recursion
Calculate
, and record the state
,
,
.
(3) Termination
The recursion ends when
. The probability of the most likely path is found by
. The state of this path at variable
is found by
.
(4) Backtracing
The state of the optimal path at variable
is found by
,
.
EM Algorithm
Given a set of examples from a sequence and the HMM structure, the EM algorithm can be implemented for model fitting. The EM algorithm is an iterative method to find the maximum likelihood estimate(s) (MLE) based on the following principle:32 From the Kullback-Leibler divergence theory,32 the expected log-likelihood function of the complete data (consisting of the observed data, known as incomplete data, and the unobserved latent data) is a lower bound on the log-likelihood of the observed data, that is, the log-likelihood function of the complete data under any set of probability distribution of hidden data is less than or equal to the log-likelihood of the observed data. Therefore, we can use the expected log-likelihood function of the complete data as a working function, iteratively approaching to the log-likelihood of the observed data, the true objective function, and thereby finding the MLE. The EM algorithm alternate between performing an expectation step (E-step) and a maximization step (M-step). In an E-step, the expectation of the log-likelihood of complete data is evaluated using the current estimate for the parameters to create a function for maximization, and in an M-step, the parameters maximizing the expected log-likelihood found in the E-step are computed. It can be proved that such an iteration will never decrease the objective function, assuring the EM converges to an optimum of the likelihood. The EM algorithm will be very efficient in particular for the cases when there is the closed-form solution to MLE for the complete data. The EM algorithm includes three steps of initialization, a series of iterations, and termination.
(1) Initialization
Given a set of initial parameter values
, start the EM iterations.
Iteration
Each cycle of EM iteration involves two steps, an E-step followed by an M-step, alternately optimizing the log-likelihood with respect to the posterior probabilities and parameters, respectively.
E-step: Calculate the posterior probability of latent data using the current estimate for the parameters,
. Specifically, as mentioned in the forward-backward algorithm, compute the forward probabilities and the backward probabilities for each sequence of observations (
,
,…,
) using the current estimate. Further, calculate the posterior state probabilities of a variable and of the state combinations of two adjacent variables as follows,
,
,
,
,
,
,
.
To perform the E-step will assure that the expected log-likelihood function will be maximized under the current estimated parameters
. Then, the function for the expectation of the log-likelihood of complete data is computed by using the estimated posterior probabilities of hidden data.
M-step: Estimate the new parameters that maximize the expected log-likelihood found in the E-step. When the complete data are available, the estimation of parameters in a HMM is straightforward; for example, the initial state probability
(
) can be calculated from
by the counting method, the transition probability
(
,
,
) can be calculated from
by the counting method, the emission parameter
(
,
) can be found from
and observation
, depending on the form of emission probability function. To perform the M-step will assure that the likelihood of complete data computed from the E-step will be maximized with respect to the parameters.
Termination
Repeat the E-step and the M-step until convergence is reached such as the objective function does not increase or the parameter estimation does no longer change.
In theory, extension of the above 1-D methods to higher dimensional HMMs and hidden MRFs is straightforward. In practice, such an extension is not easy to implement. One solution is to convert a multi-dimensional model into a 1-D multi-dimensional vector Markov model by considering the set of nodes with a fixed coordinate along a given direction (e.g., horizontal, vertical, or diagonal in a regular plane) as a new vector node. For example, the rows, the columns, and the anti-diagonal and its parallelisms of a 2-D lattice respectively form super nodes, generating a vector Markov chain.34–38 Generalization to the 3-D case is also straightforward.39–41 Then, the forward-backward algorithm, the Viterbi algorithm, and the EM algorithm can be applicable to the new HMM. The main limitation of these approaches is that, although avoiding exhaustive computations along the chosen dimension, it is still necessary to consider all the possible combinations of states in the resulting vector and thus the complexity is lessened only from one direction; in other words, the computational complexity of the algorithms grows exponentially with the data size in the other dimension(s), e.g., the number of rows, the number of columns, or the minimum of them in the 2-D lattice,34,42,43 making the computations intractable in most cases of interest. Alternatively, restricted models with reduced connectivity such as pseudo multi-dimensional HMMs,44,45 embedded HMMs,46,47 dependence-tree HMMs48 are suggested for use. One of the major shortcomings is that the dependence of a node on its neighbors in a fully connected multi-dimensional HMM does not guarantee to be explored. Several attempts have also been done to heuristically reduce the complexity of the HMM algorithms by making simplifying assumptions.34,36,42,43,49–52 The main disadvantage of these approaches is that they only provide approximate computations, such that the probabilistic model is no longer theoretically sound.
On hidden MRFs, there are also a few methods applicable to exact computation such as variable elimination methods (an analogue to the forward-backward algorithm) and belief propagation methods (sum-product message passing and max-product message passing methods corresponding to the forward-backward and the Viterbi algorithms, respectively).53 However, the exact inference for hidden MRFs and higher dimensional HMMs is a nondeterministic polynomial time-hard (NP-hard) problem. It is believed that there exists no general method efficiently for exact computation of hidden MRFs and higher dimensional HMMs. In most cases, exact inference is not allowed because of tremendous computational burden. Several approximate inference approaches and numerical computing techniques such as Markov chain Monte Carlo sampling,54 variational inference,55 and loopy belief propagation56,57 methods are more feasible.
My research team, funded by an NSF grant, is developing a telescopic algorithm which can make full use of the property of conditional independence in the models and is expected to increase the computational complexity linearly (rather than exponentially) with the sizes of both dimensions in a 2-D HMM, thus greatly lowering the cost in computing resources including computer memory and computing time and being applicable to exact computation in an iterative way for statistical inference of high dimensional HMMs.
Applications to biological studies
HMMs offer an effective means for prediction and pattern recognition in biological studies. Since it was introduced to computational biology by Churchill for the first time,58 HMM has emerged as a promising tool for diverse biological problems and there have been an expanding list of applications in biology.59,60 Here highlight the major applications across the various biological research areas.
Genetic mapping
Genetic mapping includes linkage map construction and gene mapping, is to place a collection of genetic loci such as genes, genetic markers, and other forms of DNA segments, onto their respective positions on the genome, based on the information of meiotic crossover (recombination between the homologous chromosomes). Genetic mapping is the basis of map-based (positional) cloning, marker-assisted selection, and forward genetics.
Gene transmission from parent to offspring at multiple genetic loci is by nature a 2-D Markov process where, along the generation (vertical) dimension, given the genotypes of parents, the genotype of an offspring is independent of his/her other ancestors, and along the chromosome (horizontal) dimension, given the inheritance state of a locus (to denote whether the paternal allele and the maternal allele are grand-paternally or grand-maternally inherited), the inheritance state at its one side locus is independent of that at its other side locus assuming no crossover interference (otherwise, it will be a higher order Markov process). The ordered alleles or inheritance state of an individual at a locus can be viewed as a node in a 2-D Markov mesh. However, the genotype at a gene, the ordered genotype and the inheritance states at an either genetic marker or gene are usually not directly observed. Thus, gene transmission is a 2-D hidden Markov process. Two seminal algorithms, the Elston-Stewart algorithm61,62 and the Lander-Green algorithm,63 are the major tools for genetic reconstruction and extracting inheritance information, laying the cornerstones in genetic mapping. The most popular analytical methods and software packages are derived from them, for example, the former including FASTLINK64–66 and VITESSE,67 and the latter including GENEHUNTER,68 MERLIN,69 and ALLEGRO.70,71 But both the algorithms use the strategy that converts 2-D model to 1-D vector model—the Elston-Stewart algorithm and the Lander-Green algorithm correspond to the 1-D row-vector and column-vector HMMs, respectively. Therefore, both categories of approaches have their intrinsic weaknesses: the Elston-Stewart algorithm is only applicable to a handful of genetic loci, because of growing computational complexity exponentially with the number of loci, while the Lander-Green algorithm is only applicable to relatively small pedigrees, because of growing computational complexity exponentially with the number of nonfounders in a pedigree. It is expected that the telescopic algorithm being developed will offer a solution to circumventing the limitations of the Elston-Stewart and the Lander-Green algorithms.
A simple pedigree consisting of four generations and seven individuals shown in Figure 3B is used to illustrate its correspondence to the 2-D HMM in Figure 3A. In the dimension of time (along the generation), the marriage nodes 1 × 2, 3 × 4, and 5 × 6, respectively, correspond to the first three rows in Figure 3A, while the individual 7 corresponds to the last row. In the dimension of space (along a chromosome), the genetic loci either marker or gene in Figure 3B correspond to the columns in Figure 3A. In the absence of both crossover interference and higher order linkage disequilibrium, it is a 2-D HMM of order one. The two-tuple state variable consisting of the ordered genotype and inheritance state is hidden, of which the state number varies from node to node depending on the allele number at a locus and the parental genotypes. The transition probability along the first row is determined by the linkage disequilibrium parameters between two contiguous loci or haplotype frequencies as both the individuals of this marriage node are founders; those along the second and the third rows are determined by the linkage disequilibrium coefficients and the recombination rate as one individual of that node is a founder and the other is a nonfounder; and that along the fourth row is determined by the recombination rate as the only individual of that node is a nonfounder. The transition probability along the column is either 0.25 (equi-probable transmission) if the states between the parents and the offspring are compatible or 0 otherwise. The emission parameters depend on the type of locus. For a genetic marker, they take the value of 1 if the hidden state is compatible with the marker observation or 0 otherwise. For a gene locus, they are the penetrance or other proper probabilistic function linking a genotype to the phenotype. A general pedigree also corresponds to a similar 2-D HMM. Given the straightforward correspondence between 2-D HMMs and pedigrees, the telescopic algorithm can be adapted into the genetics context to invent an innovative genetic reconstruction engine, and the inheritance processes can be restored in the statistical sense. Based on the reconstructed inheritance processes, genotypic similarity between relatives can be evaluated in terms of the distribution of the hidden state variable at a certain locus (or loci) and it is in principle feasible to develop powerful parametric and nonparametric methods to test linkage, association or both.
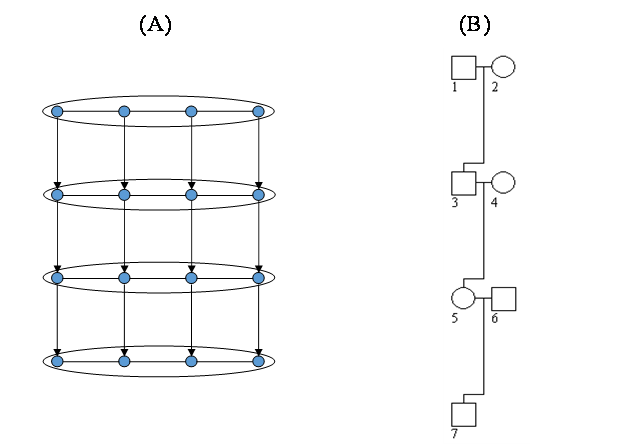
Figure 3 An illustrative diagram for the correspondence between an 2-D HMM and its corresponding pedigree: (A) the 2-D HMM of size and (B) a simple pedigree with four generations.
Biological sequence analysis
Protein and nucleic acid including DNA and RNA are linearly ordering sequences of monomers such as amino acids and nucleotides. The primary structure of a biological macromolecule (i.e., the linear sequence of monomer units) is the 3-D structural and functional basis, determining the higher order structure and 3-D shape/conformation in living systems and hence defining its function. Biological sequence is not only important in the description of biological polymer but also the basic information-bearing entity on its biological role. Biological sequence analysis can shed light on its features, structure, function, and evolution.
New sequences are adapted from pre-existing sequences rather than invented de novo. During a long-term evolutionary course, induced by the biotic and abiotic agents, the ancestral sequence may undergo mutation, recombination, and insertion/deletion which is further subjected to certain evolutionary forces such as selection and genetic drift, to develop into the extant sequences. Because of certain biological mechanisms such as triplet codon, dinucleotide tract (e.g., CpG islands), and the sequence consensus due to the conserved functional domain, there also exist immanent associations between sequence units. It has also been demonstrated that a biological sequence is not a completely random arrangement.72 Haussler et al. reported that HMM biological sequence such as protein and DNA could be characterized by a HMM, where match (including identity and substitution) and gap (i.e., insertion/deletion) occurred in each site can be considered as a hidden state that satisfies the Markov structure, while the sequence of monomers are the observation data emitted from a set of state-dependent probability distributions.73 HMMs are recognized as a powerful analytical tool and are extensively used for pattern recognition in a single sequence such as direct repeats and characteristic subsequence, sequence alignment, sequence classification, similarity query, or homology detection.74–77
Sequence alignment is to arrange a pair/group of biological sequences next to one another so that their most similar elements are juxtaposed, and thereby to identify regions of similarity that may be a consequence of structural, functional, or evolutionary relationships among the sequences. Alignments are conventionally shown as a traces or a position-specific scoring table (also known as a profile), where the aligned sequences are typically represented as rows within a matrix and gaps may be inserted between the units so that each element in a sequence is either a match or a gap and identical or similar elements are aligned in successive columns. If the aligned sequences share a common ancestry, mismatches can be interpreted as point mutations and gaps correspond to insertion or deletion mutations introduced in one or more lineages. Successful alignments are a prerequisite for many bioinformatics tasks such as pattern recognition, characteristic subsequence extraction, and motif search. Computational approaches to sequence alignment generally fall into global (full-length) and local alignments, and pairwise and multiple sequence alignments. Global alignment is to align every element in all analyzed sequences so that it needs to consider all mismatches and gaps across the entire length. A global alignment is best for describing relationship and inferring homology between query biological molecules. Local alignment attempts to align only parts of the query sequences (subsequences) and to identify regions of similarity or similar sequence motifs within long sequences. Local alignments are often preferable because it is common that only parts of compared sequences are homologous (e.g., they share one conserved domain, whereas other domains are unique), and, on many occasions, only a portion of the sequence is conserved enough to carry a detectable signal, whereas the rest has diverged beyond recognition. Multiple sequence alignment is an extension of pairwise alignment to incorporate more than two sequences at a time. Although multiple sequence alignment shares the same principle as pairwise alignment, the algorithmic complexity for exact computation increases exponentially with the number of query sequences, and thus it is usually implemented by heuristic and progressive algorithms. Several common methods include Needleman-Wunsch algorithm78 for pairwise global alignment, Smith-Waterman algorithm79 for pairwise local alignment, Feng-Doolittle algorithm80 for progressive multiple sequence alignment, and the profile analysis81 for aligning a family of similar sequences, finding distantly related sequences, and identifying known sequence domains in new sequences by sequence comparison. However, these standard methods highly depend upon the choice on substitution/scoring matrix (e.g., Dayhoff mutational distance matrix in protein sequence) and gap penalties that seems to be somewhat subjective and arbitrary. Application of HMMs to sequence alignment may circumvent the limitations in the traditional methods. In the HMM context, an alignment can be viewed as a series of nodes, each of which corresponds to a position (column) in the alignment and may take one of three hidden states: match, insertion, and deletion. A set of transition probabilities specifies the potential transition from one state to another in a move along the sequence of positions. A match state and an insertion state will emit an output token from a set of possible symbols (e.g., nucleotides and amino acids) according to their respective emission probabilities, while a deletion state will be silent. The HMM can be trained on unaligned sequences or pre-constructed multiple alignments, and the model parameters including transition probabilities between match, insertion, and deletion, and the state-specific emission probabilities can be learned from the training data. Once training is done, the optimal state path for each sequence can be decoded based on the fitted model and the similarity between sequences can also be evaluated based on the (log) p-value. Compared with the customary methods, the HHM-based methods not only are well grounded in probability theory and have a consistent probabilistic basis behind gap penalties and substitution scores, in general, producing a better result, but also run in an automatic regime and thus require less skill.82,83
After a profile or traces is constructed for a group of related sequences derived from a common ancestral sequence, likewise, the HMM can be applied to extract consensus segments, to create a retrieval database, to capture information about the degree of conservation, to find the family of sequences, to test the similarity of new sequences to a group of aligned sequences (probe), and further to classify sequences, to infer the evolutionary relationship, and to construct a phylogenetic tree.
Gene finding and feature discovering
In computational biology, gene finding or gene prediction is to identify the coding regions or genes from genomic DNA, also known as genomic annotation.84–87 There are two categories of methods for gene prediction. One is called the ab initio methods, which find gene(s) by systematically searching the genomic DNA alone for certain signals and statistical properties of protein-coding genes. A gene is composed of specific structures including promoter sequence, start codon, exon, intron, stop codon, and untranslated region. There are certain sequences of features in these regions such as the donor (GT dinucleotide) and acceptor (AG dinucleotide) in an intron. Furthermore, protein-coding DNA has certain periodicities and other statistical properties. Thus, HMM can be used for gene discovery. The principle is that by considering the gene structures and characteristic subsequneces as hidden states and the genomic DNA as the observed symbols, gene prediction is, similar to the natural language recognition, a decoding problem for a hidden Markov process. Specifically, the HMM is fitted by using a set of annotated sequences (i.e., sequences with known coding and noncoding regions); then find the most likely hidden states for a new sequence based on the trained HMM. Such a principle of prediction is also applicable to other bioinformatics analyses including functional domain finding, sequence pattern extraction, motif search, and identification of CpG island, open reading frame, transcription factor binding site, cis-regulatory module, and noncoding RNA.88
A hypothetical example is used here to illustrate the application of the Viterbi decoding algorithm to identifying the CpG island, a region of DNA with a high frequency of CpG sites where a cytosine nucleotide is followed by a guanine nucleotide in the linear sequence of bases along its 5' → 3' direction. As cytosines in CpG dinucleotides are vulnerable to methylation that can change with a high chance into a thymine by accidental deamination, the CG dinucleotide frequency in genomic DNA is often much smaller than expected. However, methylation is often suppressed in the promoter regions of active genes, and therefore those regions often have much higher CpG frequency than elsewhere in the genome. CpG islands, at least 200 (typically 300-3,000) base pairs in length with a GC content of greater than 50% and a ratio of observed-to-expected CpG number above 60%, are often associated with the start of the gene (promoter regions) in the most mammalian genome and thus the presence of a CpG island is an important signal for gene finding. HMM is a powerful approach to determine whether a short DNA segment comes from a CpG island or not, and to find all contained CpG islands in a long genomic segment. There are several choices on HMM for CpG islands. Assume a HMM, as shown in Figure 4, is available (or has been already trained from a set of empirical observations), in which there are two hidden states (CpG, denoted by “+”, and non-CpG, denoted by “−“) with the initial state, transition, and emission probabilities, respectively. The Viterbi algorithm is used to find the most probable path of states for the following short sequence (generated from the website: http://statgen.ncsu.edu/sblse/animations/cgIsland.html):
TCTCGCTGCCGCCAACCCTCGGCGCCGTCGGGTTCGCCGCGGCTCTGATAAGTCCCGT
TTATGGTACCCGGGCCGATCTCTGGTGGGAATCGGAGACCTGTGTACCCTGACGCATC
CGTTTGTGTTCCCTACACGGCCGACGCAGACCGGGCGCGCGGCGCCACCCAACGAAGC
CCGGGTATGGCACGTGCCCCAGGCGGTGCCCTACCCGTATTTCGGGACAAGTTCCCGG
ATCGGGTGAAAGTTAACGGAAGGATGCCAAGCAATAGCGGCCACAGGACCCGCCTGGC
GACGCATGGACTGGATCCGGAGGTCTGGCCAACAGTTGATTTCATGGGTTACAGCCCC
GGTGTAGATCCCCTCATGGTCTCCCGAACCGATTAGTTTGAAAACTGTATCTCCTGGC
CGCCTAACAGGTATAAAGAGCCGGCTCACACTGGGGTGAGGGGGCGCGTGGCCCCCTT.
The Viterbi algorithm is implemented as follows. (For ease of notation, the logarithm of the probability is used here.)
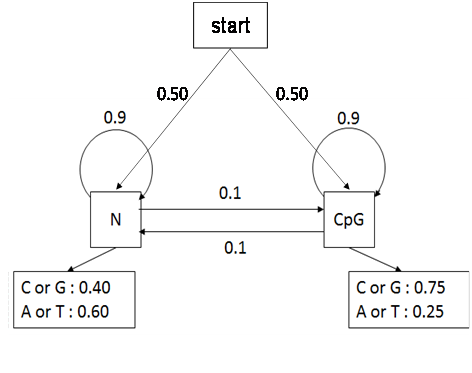
Figure 4 A hypothetical hidden Markov model for CpG island.
(1) Initialization
and
,
and
,
(2) Recursion
and
,
and
;
and
,
and
;
and
,
and
;
…
(3) Termination
When the last symbol is reached,
and
,
and
.
Therefore, the probability of the most likely path is
and the state of this path at position 463 is “+”. A tabular illustration of the Viterbi algorithm is shown in Table 1.

Table 1 The implementation of the Viterbi algorithm for the hypothetical example
(4) Backtracing
Finally, the best path of states can be identified as follows:
++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++--+++
-++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++++++++++++++++++++++++++++-++++++++++++++++++---++++++++-+++
+++++---+++++++++++++++++++++++++++++++++++++++++++++++++++++++++
+++++--+--+++++-+-++++++++++++++++++++++++++++++++++++++++++--+--
--+-+---+-++++++++++++++++++++---+-++++++++++++++++++++++++++++++
+++++++++,
where “+” denotes a CpG state and “−“ denotes a non-CpG state in the path. There is a large proportion of CpG states in the best path, suggesting that this sequence may be a CpG island.
The other category is called the homology-based methods for gene discovery, also known as the comparative genome approaches or the empirical methods. They predict potential gene structure and infer the gene function based on the similarity and homology between a new sequence and the known sequences assessed from a sequence alignment analysis, for which, as mentioned in the previous subsection on sequence alignment, HMMs are an effective means. The homology-based methods are also applicable to identification of regulatory genes, detection of open reading frames, exploration of junk genes, and others.
Molecular structure prediction
The high level structure of a biological macromolecule, such as the DNA double helix and supercoiling (superhelicity), the RNA stem-loop, and the protein α-helix, β-sheet, β-turn, spatial arrangement, and spatial structure of the complex of subunits, is highly related to its 3-D conformation and molecular interaction, and thus plays a very important role in its biological activities and stability. The higher order structure of macromolecules is governed by foundational principles of chemistry and physics, and can be predicted by the primary structure. HMMs offer an effective solution to predict the potential higher order structure and dynamics of a biological molecule from its linear sequence.89–91 In essence, such a prediction is a pattern recognition issue by modeling the structural elements such as the α-helix, β-sheet, and β-turn, as hidden data and the linear sequence of units as the observation data. A set of sequences with known high level structure are used for an HMM learning and finding the best fit parameters. Then the trained model is used to predict the hidden states of a target sequence.
Biological image analysis
Images generated from modern imaging platforms such as computer tomography, magnetic resonance imaging, and ultrasound imaging are been accumulating at an explosive pace, representing an important category of biological data. Computerized image analysis is a research hotspot being actively explored in biology.92,93 There usually exist temporal and/or spatial dependencies among the pixels in an image or images,94 for example, there will be spatial correlations between the pixels in an image and temporal correlation between the pixels in the images taken at different time points. HMM or hidden MRF can well model the correlation structure with random noise. As improved methods, HMMs have been intensively applied to diverse image analyses including image segmentation, image noise filtering, image retrieval, image classification, and image recognition.24,56,95,96 Within the HMM, the feature of a pixel, usually denoted by a vector quantization for color, greyscale, texture, and shape, is viewed as a random variable with noise, while a Markov mesh is used to model the spatial structure and conditional independencies. Hence, the HMM can well describe the statistical properties of an image and then used to fit the digital image data. The general steps include: to collect a volume of images as training data, to extract the feature information for each pixel such as grey value and texture, to define a HMM structure such as hidden states, to implement model learning using training data, and further to perform image segmentation, classification, and pattern recognition for query images, or feature extraction for database retrieval and search.
Epidemiological prediction
Many epidemic and etiological processes such as infectious disease transmission and chronic disease progression are a multi-state and multi-stage Markov process, that is, the future epidemic outbreak or disease status depends on the current state, not on the past, because communicable pathogen dispersion in population and pathogen multiplication and spread in body satisfy a temporal/spatial Markov dependence. On the other hand, however, not all data are perfectly recorded in many cases and thus the variables of interest may be latent; for example, the exact time at onset of a patient cannot be determined because examination or follow-up is conducted at limited time points, and epidemic dynamics are not available for all geographical regions and years in a survey. HMM can well model the epidemic dynamics, the progression of a chronic disease, and the geographical distribution of a disease, and are very useful for epidemiological analysis, prediction, and surveillance.97–102 The main steps include: to collect data on epidemic survey or chronic disease status, to define hidden states such as epidemic and non-epidemic states, and healthy and disease phases (more flexibly, the number of hidden states is not necessarily predefined in a HMM), to train the HMM and estimate parameters, and to use the fitted model for prediction or disease map. Further, some putative risk factors can be introduced to a HMM via building a set of transition probabilities that are subject to these risk factors, in order to identify risk factor(s) and/or improve the prediction accuracy.
Phylogenetic tree construction
Similar to gene transmission from generation to generation, molecular evolutionary course is a combination of double Markov processes—one that operates in the dimension of space (along a genome) and one that operates in the dimension of time (along the branches of a phylogenetic tree).103 Compared with the traditional evolutionary models that ignore the dependencies between genetic loci, a phylogenetic HMM can express the true relationship more accurate and thereby usually give better results.104,105 This category of models are also used for epitope discovery.106 Moreover, HMMs are applicable to handling the ambiguity in evolution and comparative genomics analysis due to missing data107 and heterogeneity in evolutionary rate.108
Text mining
While the rapidly increasing text data such as biological literature, medical documents, and electronic health records provide a large amount of material for evidence-based practice and data-driven research, it is a key step to harness the massive text data and extract useful information effectively. Automatic text mining is an effective means of gaining potentially useful knowledge from a large text database.109 HMM is a powerful approach for text mining, information retrieval, and document classification.110-112 The basic idea is that a paper and a clinical record contain several semantic tags such as symptom, therapy, and performance, or index fields such as title field, author field, the content of which is the phrase of interest. Extraction of information is first to determine the index field, and then to grab the phrases. Such a process corresponds to an HMM: the index fields represent the combination of hidden states, and the corpus consisting of words/phrases are the observed symbols, and thus the HMM may be used for text mining. Specifically, the steps can be summarized as follows: to define a HMM and choose the HMM structure, to label a set of known papers or documents as the training corpora, to train the model using the tagged examples, and then to use the learned model to find the best label sequence for a query document and output the phrases in the desired fields, achieving the text mining.
Future prospect
Organism is a multi-level and modularized intricate system that is composed of numerous interwoven metabolic and regulatory networks. During the long period of evolution, functional associations and random evolutionary events result in elusive molecular, physiological, metabolic, and evolutionary relationships. It is a daunting challenge for biological studies to decipher the complex biological mechanisms and crack the codes of life. Recent technological advances, including innovations in high-throughput experimental methods such as genomics, transcriptomics, epigenomics, proteomics, and metabolomics, provide powerful discovery tools for biological studies, enabling dissecting the multi-level modular networks and tracing the historical events. However, the analyses of systems biology, computational biology, and bioinformatics, play an indispensable role in extracting knowledge from massive data and assembling a comprehensive map underlying a biological system. A HMM not only is allowed to model random noises but also can capture the intrinsic dependencies between units, so that many biological mechanisms or phenomena can be characterized by a HMM. Recently HMMs have demonstrated a tremendous potential in genetic network analysis and integration of multi-omics data.113–115 Thus, HMMs, as a powerful tool to tackle complicated analytical problems, are expected to have more compelling applications in biology.
Acknowledgments
The author likes to thank Tingting Hou and Shouye Liu for their contributions to this study. This project was supported in part by NSF grant DMS1462990 and UAMS Research Scholar Pilot Grant Awards in Child Health G1-51898 to X.-Y.L. The author declares no conflict of interest on this work.
Conflicts of interest
References
- Basharin GP, Langville AN Naumov VA. The life and work of AA Markov Linear Algebra and its Applications. 2004;386:3–26.
- Shannon CE. A Mathematical Theory of Communication. Bell System Technical Journal. 1948;27(3):379–423.
- Bharucha-Reid AT. Elements of the theory of Markov processes and their applications. Mc Graw-Hill; 1960.
- Grassly NC, Fraser C. Mathematical models of infectious disease transmission. Nat Rev Microbiol. 2008;6(6):477–487.
- Balzter H . Markov chain models for vegetation dynamics. Ecological Modelling. 2000;126(2–3):139–154.
- Billingsley P. Statistical methods in markov chains. The Annals of Mathematical Statistics. 1961;32(1):12–40.
- Ephraim Y, Merhav N. Hidden Markov processes. IEEE Transactions on Information Theory. 2002;48(6):1518–1569.
- Vidyasagar M. Hidden markov processes: theory and applications to biology. Princeton University Press; 2014.
- Dymarski P. Hidden markov models, theory and applications. hidden markov models, theory and applications, In: Dymarski. editor. InTech.
- Ching WK. Markov chains: models, algorithms and applications. 2nd ed, New York: Springer. 2013.
- Rabiner L Juang B. An introduction to hidden Markov models. IEEE ASSP Magazine. 1986;3(1):4–16.
- Woods JW. Two-dimensional discrete Markovian fields. Information Theory, IEEE Transactions on. 1972;18(2):232–240.
- Fornasini E. 2D Markov-Chains. Linear Algebra and Its Applications. 1990;140:101–127.
- Politis DN. Markov-chains in many dimensions. Advances in Applied Probability. 1994;26(3):756–774.
- Derin H, Kelly PA. Discrete-index Markov-type random processes. Proceedings of the IEEE. 1989;77(10):1485–1510.
- Abend K, Harley T, Kanal L. Classification of binary random patterns. IEEE Transactions on Information Theory. 11(4):538–544.
- Gray AJ, Kay JW, Titterington DM. An empirical study of the simulation of various models used for images. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1994;16(5):507–513.
- LEVY PA. Special problem of Brownian motion, and a general theory of Gaussian random functions. in Proceedings of the Berkeley Symposium on Mathematical Statistics and Probability. University of Caifornia Press; 1956.
- Kindermann R, Snell JL. Markov random fields and their applications. American Mathematical Society Providence, RI 1; 1980.
- Shakya S, Santana R. Markov Networks in Evolutionary Computation. Springer Berlin Heidelberg; 2012.
- Smyth P. Belief networks hidden Markov models, and Markov random fields: A unifying view. Pattern Recognition Letters. 1997; 18(11-13):1261–1268.
- Michael I Jordan MI. Graphical models. Statistical Science. 2004;19(1):140–155.
- Kunsch H, Geman S, Kehagias A. Hidden markov random fields. 1995;5(3):577–602.
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20(1):45–57.
- Stratonovich R. Conditional markov processes. Theory of Probability & Its Applications. 1960;5(2):156–178.
- Rabiner LR. A Tutorial on hidden markov-models and selected applications in speech recognition. Proceedings of the Ieee. 1989; 77(2):257–286.
- Viterbi A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory. 1967;13(2):260–269.
- Viterbi AJ. A personal history of the Viterbi algorithm. IEEE Signal Processing Magazine. 2006;23(4):120–142.
- Forney GD. The viterbi algorithm. Proceedings of the IEEE. 1973;61(3):268–278.
- Baum LE, Petrie T. Statistical inference for probabilistic functions of finite state markov chains. The annals of mathematical statistics. 1966;37(6):1554-1563.
- Baum LE. A maximization technique occurring in the statistical analysis of probabilistic functions of markov chains. The Annals of Mathematical Statistics. 1970;41(1):164–171.
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the em algorithm. Journal of the Royal Statistical Society. Series B (Methodological). 1977;39(1):1–38.
- Kullback S, Leibler RA. On Information and Sufficiency. 1951;22(1):79–86.
- Li J, Najmi A, Gray RM. Image classification by a two-dimensional hidden Markov model. IEEE Transactions on Signal Processing. 2000; 48(2):517–533.
- Li YJ. An analytic solution for estimating two-dimensional hidden Markov models. Applied Mathematics and Computation. 2007; 185(2):810–822.
- Devijver. Probabilistic labeling in a hidden second order markov mesh. in pattern recognition in practice ii amsterdam: North Holland. 1985.
- Du S, Wang J, Wei Y. New learning algorithms for third-order 2-D hidden Markov models. International Journal of Advancements in Computing Technology. 2011;3(2):104–111.
- Ma X, Schonfeld D, Khokhar A. A General two-dimensional hidden markov model and its application in image classification. in IEEE International Conference on Image Processing (ICIP2007); 2007.
- Qian W, Titterington DM. Pixel labelling for three-dimensional scenes based on Markov mesh models. Signal Processing. 1991; 22(3):313–328.
- Joshi D, Li J, Wang JZ. A computationally efficient approach to the estimation of two- and three-dimensional hidden Markov models. IEEE Transactions on Image Processing. 2006;15(7):1871–1886.
- Li J, Joshi D, Wang JZ. Stochastic modeling of volume images with a 3-D hidden Markov model. in Image Processing, ICIP '04. 2004 International Conference on; 2004.
- Sargin ME, Altinok A, Rose K, et al. Conditional Iterative decoding of two dimensional hidden markov models, in 15th IEEE International Conference on Image Processing (ICIP 2008); 2008..
- Baumgartner J, Ana Georgina Flesia, Javier Gimenez, et al. A new approach to image segmentation with two-dimensional hidden Markov models. 2013 BRICS Congress on Computational Intelligence & 11th Brazilian Congress on Computational Intelligence. 2013;21–-222.
- Werner S Rigoll G. Pseudo 2-dimensional hidden Markov models in speech recognition. in IEEE Workshop on Automatic Speech Recognition and Understanding (ASRU'01) IEEE. 2001.
- Lin HC, Wang LL, Yang SN. Color image retrieval based on hidden Markov models. IEEE Transactions on Image Processing. 1997; 6(2):332–339.
- Kuo SS, Agazzi OE. Keyword spotting in poorly printed documents using pseudo 2-D hidden Markov models. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1994;16(8):842–848.
- Nefian AV, Hayes MH III. Face recognition using embedded hidden markov model. IEEE Conference on Audio and Video-based Biometric Person Authentication; 1999.
- Merialdo B, Jiten J, Huet B. Multi-dimensional dependency-tree hidden markov models. in International Conference on Acoustics, Speech, and Signal Processing; 2006.
- Dementhon D, Doermann D, Stuckelberg MV. Hidden Markov Models for Images, in Int. Conf. on Pattern Recognition; 2000.
- Merialdo B, Marchand-Maillet S, Huet B. Approximate Viterbi decoding for 2D-hidden Markov models. in IEEE International Conference on Acoustics, Speech, and Signal Processing ( ICASSP '00); 2000.
- Perronnin F, JL Dugelay Rose K. Deformable face mapping for person identification. in Image Processing, 2003. ICIP 2003. Proceedings International Conference on; 2003.
- Baggenstoss PM. Two-Dimensional Hidden Markov Model for Classification of Continuous-Valued Noisy Vector Fields. IEEE Transactions on Aerospace and Electronic Systems. 2011;47(2):1073–1080.
- Koller D, Friedman N. Probabilistic Graphical Models: Principles and Techniques. MIT Press; 2009.
- Brooks SP. Markov chain monte carlo method and its application. journal of the royal statistical society series d-the statistician. 1998; 47(1):69–100.
- Jordan MI. An introduction to variational methods for graphical models. Machine Learning, 1999;37(2):183–233.
- Blake A, Kohli, Rother C. Markov Random Fields for Vision and Image Processing. MIT Press; 2011.
- Wang C, Paragios N. Markov random fields in vision perception: A survey, in Rapport de recherche. 2012.
- Churchill GA. Stochastic models for heterogeneous DNA sequences. Bull Math Biol. 1989;51(1):79–94.
- Choo KH, Tong JC, Zhang L. Recent applications of Hidden Markov Models in computational biology. Genomics Proteomics Bioinformatics. 2004;2(2):84–96.
- Koski T. Hidden markov models for bioinformatics. Springer Netherlands; 2001.
- Elston RC, Stewart J. A general model for the genetic analysis of pedigree data. Hum Hered. 1971;21(6): 523–542.
- Cannings C, Thompson EA, Skolnick MH. Probability functions on complex pedigrees. Advances in Applied Probability. 1978; 10(1):26–61.
- Lander ES, Green. Construction of multilocus genetic linkage maps in humans. Proc Natl Acad Sci USA. 1987;84(8):2363–2367.
- Cottingham RW, Idury RM, Schaffer AA. Faster Sequential Genetic-Linkage Computations. American Journal of Human Genetics. 1993;53(1):252–263.
- Schaffer AA. Faster linkage analysis computations for pedigrees with loops or unused alleles. Hum Hered. 1996;46(4):226–325.
- Schaffer AA. Avoiding recomputation in linkage analysis. Hum Hered. 1994;44(4):225–237.
- O'Connell JR, Weeks DE. The VITESSE algorithm for rapid exact multilocus linkage analysis via genotype set-recoding and fuzzy inheritance. Nat Genet. 1995;11(4):402–408.
- Kruglyak L.Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet. 1996;58(6):1347–6133.
- Abecasis GR. Merlin-rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet. 2002;30(1):97–101.
- Gudbjartsson DF. Allegro version 2. Nat Genet. 2005;37(10):1015–1016.
- Gudbjartsson DF. Allegro a new computer program for multipoint linkage analysis. Nat Genet. 2000; 25(1):12–13.
- Gentleman JF, Mullin RC. The Distribution of the frequency of occurrence of nucleotide subsequences, based on their overlap capability. Biometrics. 1989;45(1):35–52.
- Modeling. Journal of Molecular Biology. 1994;235(5):1501–1531.
- Karlin S. New approaches for computer analysis of nucleic acid sequences. Proc Natl Acad Sci USA. 1983;80(18):5660–5664.
- Hughey R, Krogh A. Hidden markov models for sequence analysis: extension and analysis of the basic method. Comput Appl Biosci. 1996;12(2):95–107.
- Yoon BJ. Hidden markov models and their applications in biological sequence analysis. Curr Genomics. 2009;10(6): 402–415.
- Eddy SR. Hidden markov models. Curr Opin Struct Biol. 1996;6(3):361–365.
- Needleman SB, Wunsch CD. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology . 1970;48(3):443–453.
- Smith TF, Waterman MS. Identification of common molecular subsequences. Journal of Molecular Biology. 1981;147(1):195–197.
- Feng DF, Doolittle RF. Progressive sequence alignment as a prerequisite to correct phylogenetic trees. J Mol Evol. 1987;25(4):351–360.
- Gribskov M, McLachlan AD, Eisenberg D. Profile analysis: detection of distantly related proteins. Proc Natl Acad Sci USA. 1987; 84(13):4355–4358.
- He M Petoukhov S. Mathematics of bioinformatics: theory, methods and applications. Wiley; 2011.
- Mount DW. Using hidden markov models to align multiple sequences. Cold Spring Harb Protoc. 2009(7):41.
- Krogh A, Mian IS, Haussler D. A hidden Markov model that finds genes in E. coli DNA. Nucleic Acids Res. 1994;22(22):4768-4778.
- Lukashin AV, Borodovsky M. GeneMark.hmm: new solutions for gene finding. Nucleic Acids Res. 1998;26(4):1107–1115.
- Burge C, Karlin S. Prediction of complete gene structures in human genomic DNA. J Mol Biol. 1997;268(1):78–94.
- Pedersen JS, Hein J. Gene finding with a hidden Markov model of genome structure and evolution. Bioinformatics . 2003;19(2):219–227.
- Bang H. Statistical methods in molecular biology. 1st ed. Methods in Molecular Biology, In: JM Walker, editor. Humana Press. XIII, 2010;636.
- Churchill GA. Hidden Markov chains and the analysis of genome structure. Computers & Chemistry. 1992;16(2):107–115.
- Goldman N, Thorne JL, Jones DT. Using evolutionary trees in protein secondary structure prediction and other comparative sequence analyses. J Mol Biol. 1996;263(2):196–208.
- Won KJ. An evolutionary method for learning HMM structure: prediction of protein secondary structure. BMC Bioinformatics. 2007; 8: 357.
- Roeder AH. A computational image analysis glossary for biologists. Development. 2012;139(17):3071–3080.
- Rittscher J. Characterization of biological processes through automated image analysis. Annu Rev Biomed Eng. 2010;12:315–344.
- Wang Y. Analysis of spatio-temporal brain imaging patterns by Hidden Markov Models and serial MRI images. Hum Brain Mapp. 2014; 35(9):4777–4794.
- Li SZ. Markov random field modeling in computer vision. Springer Japan; 2012.
- Li J, Gray RM. Image segmentation and compression using hidden markov models. Springer US. 2000.
- Le Strat Y Carrat F. Monitoring epidemiologic surveillance data using hidden Markov models. Stat Med. 1999;18(24):3463–3478.
- Cooper B, Lipsitch M. The analysis of hospital infection data using hidden Markov models. Biostatistics. 2004;5(2):223–237.
- Watkins RE. Disease surveillance using a hidden Markov model. BMC Med Inform Decis Mak. 2009;9:39.
- Green PJ, Richardson S. Hidden Markov Models and Disease Mapping. Journal of the American Statistical Association. 2002; 97(460):1055–1070.
- Jackson CH. Multistate Markov models for disease progression with classification error. Journal of the Royal Statistical Society: Series D (The Statistician . 2003;52(2):193–209.
- Cook RJ Lawless JF. Statistical issues in modeling chronic disease in cohort studies. Statistics in Biosciences. 2014;6(1):127–161.
- Nielsen R. Statistical Methods in Molecular Evolution. 2010.
- Siepel A, Haussler D. Combining phylogenetic and hidden Markov models in biosequence analysis. Journal of Computational Biology. 2004;11(2-3):413–428.
- Husmeier D. Discriminating between rate heterogeneity and interspecific recombination in DNA sequence alignments with phylogenetic factorial hidden Markov models. Bioinformatics 21 (Suppl 2). 2005;ii166–172.
- Lacerda M, Scheffler K, Seoighe C. Epitope discovery with phylogenetic hidden Markov models. Mol Biol Evol. 2010;27(5):1212–1220.
- Bykova NA, Favorov AV, Mironov AA. Hidden markov models for evolution and comparative genomics analysis. PLoS One. 2013;8(6): e65012.
- Felsenstein J, Churchill GA. A Hidden Markov Model approach to variation among sites in rate of evolution. Mol Biol Evol. 1996; 13(1):93–104.
- Aggarwal CC, Zhai CX. Mining text data. Springer. New York; 2012..
- Jang H, Song SK, Myaeng SH. Text mining for medical documents using a hidden markov model, in information retrieval technology: third Asia information retrieval symposium, AIRS 2006, Singapore, October 16-18.Proceedings, In: HT Ng. et al, editors. Springer Berlin Heidelberg: Berlin, Heidelberg. 2006;553–559.
- Yi K, Beheshti J. A hidden Markov model-based text classification of medical documents. J Inf Sci. 2009;35(1):67–81.
- Mooney RJ, Bunescu R. Mining knowledge from text using information extraction. SIGKDD Explor Newsl. 2005;7(1):3–10.
- Wei, Pan W. Network-based genomic discovery: application and comparison of Markov random-field models. Journal of the Royal Statistical Society: Series C (Applied Statistics). 2010;59(1):105–125.
- Rider AK, Chawla NV, Emrich SJ. A Survey of current integrative network algorithms for systems biology, in systems biology: integrative biology and simulation tools, In: A Prokop, B Csukás, editors. Springer Netherlands: Dordrecht. 2103;479–495.
- Wei Z, Li H. A hidden spatial-temporal markov random field model for network-based analysis of time course gene expression data. 2008;2(1):408–429.

©2017 Lou. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.




