A new distribution namely Gumbel- Pareto from Gumbel -X family¹ is introduced. Some properties including moments and order statistics are studied. A reliability measure for stress - strength analysis is derived. The method of maximum likelihood is proposed for estimating the distribution parameters.The flexibility of the new model is illustrated using two examples including Covid data.

Keywords: Gumbel distribution, gumbel - X family, gumbel – Pareto, order statistics, pareto distribution, stress - strength reliabilty, T - X family

Statistical distributions play an important role in parametric inference and are commonly applied to model real life data. In practical situations, existing standard distributions do not provide good fit to all types of real data sets. Hence statisticians are developing many new distributions which are flexible than standard distributions for the analysis of real data. New distributions are developed either by combining two or more existing distributions or by adding extra parameters to the existing distributions.

The beta generated family of distributions and Kumaraswamy generated family of distributions are generated by using distributions with support between 0 and 1 as the generator. As an extension, Alzaatreh et al.² proposed a general method by replacing the beta pdf with any non - negative continuous random variable $T$ as the generator and another function $U\left(F\left(x\right)\right)$ which satisfies the following conditions:

1. $U\left(F\left(x\right)\right)\in \left[a,b\right]$
2. $U\left(F\left(x\right)\right)$ is differentiable and monotonically non - decreasing.
3. $U\left(F\left(x\right)\right)\to a$ as $x\to -\infty \text{and} U\left(F\left(x\right)\right)\to b$ as$x\to \infty$

 The new class of distributions is defined by

$G\left(x\right)={\displaystyle {\int }_a^{U\left(F\left(x\right)\right)}r\left(t\right)dt=R\left[U\left(F\left(x\right)\right)\right]}$ (1.1)

 where $R\left(t\right)$ is the cdf and $r\left(t\right)$ is the pdf of the random variable $T$ . Here, the cdf in (1.1) is a composite function of $\left(R,U,F\right)\left(x\right)$ . The corresponding pdf is

$g\left(x\right)=\left\{\frac{d}{dx}U\left(F\left(x\right)\right)\right\}r\left\{U\left(F\left(x\right)\right)\right\}$ (1.2)

The p.d.f.$r\left(t\right)$ in (1.2) is “transformed" into a new pdf $g\left(x\right)$ through the function $U\left(F\left(x\right)\right)$ , which acts as a “transformer". That is, a random variable $X$ , “the transformer", is used to transform another random variable $T$ , “the transformed". The resulting family is known as “Transformed - Transformer" or $\text{"}T-X"$ family of distributions. A large number of distributions, continuous and discrete, can be generated by applying any two existing univariate distributions based on this method. Alzaatreh et al.² gave several choices of $U\left(F\left(x\right)\right)$ depending upon the support of the random variable $T$ .

When the support of $T$ is bounded or support of $T$ is [0,1]: In this case $U\left(F\left(x\right)\right)$ can be taken as $F\left(x\right)$ or $F^{\alpha }\left(x\right)$ . This leads to the beta - generated family of distributions.

When the support of $\left[0,\infty \right)$ is $\left[0,\infty \right)$ ,$a\ge 0$ : Without loss of generality, we assume $a=0$ . Then $U\left(F\left(x\right)\right)$ can be defined as $-log\left(1-F\left(x\right)\right)$ ,$-log\left(1-F^{\alpha }\left(x\right)\right)$ ,  and $F^{\alpha }\left(x\right)/\left(1-F^{\alpha }\left(x\right)\right)$ , where $\alpha >0$ .

When the support of $T$ is $\left(-\infty ,\infty \right)$ : Then $U\left(F\left(x\right)\right)$ can be taken as $log\left[-log\left(1-F\left(x\right)\right)\right]$ ,$log\left[F\left(x\right)/\left(1-F\left(x\right)\right)\right]$ , $log\left[-log\left(1-F^{\alpha }\left(x\right)\right)\right]$ and$log\left[F^{\alpha }\left(x\right)/\left(1-F^{\alpha }\left(x\right)\right)\right].$

In this paper, we are considering the third case, that is, the support of $T$ is $\left(-\infty ,\infty \right)$ . For that, we consider T as the most important extreme value Type I distribution known as Gumbel distribution. This distribution has many applications including, to describe extreme wind spreads, sea wave heights, floods,rainfall during droughts, electrical strength of materials, air pollution problems, geological problems, naval engineering etc. Recently, the Gumbel distribution is used for modelling covid 19 data^4,5 also.

 Al-Aqtash¹ proposed the Gumbel - X family by taking T as the Gumbel random variable

$G\left(x\right)=e^{-e^{\frac{\mu }{\sigma }}{\left(\frac{F\left(x\right)}{\overline{F}\left(x\right)}\right)}^{-1/\sigma }}$ (1.3)

 By setting $\lambda =e^{\mu /\sigma }$ the cdf reduces to

$G\left(x\right)=e^{-\lambda {\left(\frac{F\left(x\right)}{\overline{F}\left(x\right)}\right)}^{-1/\sigma }}$ (1.4)

 and the pdf is

$g\left(x\right)=\frac{\lambda }{\sigma }f\left(x\right)\frac{{\left(F\left(x\right)\right)}^{-\frac{1}{\sigma }-1}}{{\left(\overline{F}\left(x\right)\right)}^{-\frac{1}{\sigma }+1}}{e}^{-\lambda {\left(\frac{F\left(x\right)}{\overline{F}\left(x\right)}\right)}^{-1/\sigma }}$ (1.5)

 The support of the random variable associated with (1.5) and f(.) are the same.

The paper is designed as follows. In section 2, we define the Gumbel-Pareto distribution. Some structural properties including moments, quantile function and order statistics are discussed in section 3.The maximum likelihood estimation of the model parameters is discussed in section 4.The application of this distribution to two real data sets are presented in section 5. In section 6, stress - strength analysis is discussed. Finally section 7 offers some concluding remarks.

Pareto distribution is a well known distribution for its capability in modeling heavy tailed data sets especially income and wealth data. Kochanczyk and Lipniack⁶ has conducted a Pareto based evaluation of national responses to Covid - 19.

If the parent distribution is Pareto with parameters k and $\theta$ , with pdf

$f\left(x\right)=\frac{k}{\theta }{(\frac{x}{\theta })}^{-k-1},x>\theta$ (2.1)

then the cdf of the four parameter Gumbel - Pareto distribution, denoted by $GuP\left(x;\lambda ,\sigma ,k,\theta \right)$ is given by

$G_{GuP}\left(x;\lambda ,\sigma ,k,\theta \right)=e^{-\lambda {[{(\frac{x}{\theta })}^k-1]}^{-1/\sigma }},x>\theta .$ (2.2)

The corresponding pdf is given by

$g_{GuP}\left(x;\lambda ,\sigma ,k,\theta \right)=\frac{\lambda k}{\sigma \theta }{e}^{-\lambda {[{(\frac{x}{\theta })}^k-1]}^{-1/\sigma }}{[{(\frac{x}{\theta })}^k-1]}^{-1/\sigma -1}{(\frac{x}{\theta })}^{{}^{{}^{k-1}}}.$ (2.3)

The hazard function (hf) is obtained as

$h\left(x;\lambda ,\sigma ,k,\theta \right)=\frac{\frac{\lambda k}{\sigma \theta }{e}^{-\lambda {[{(\frac{x}{\theta })}^k-1]}^{-1/\sigma }}{[{(\frac{x}{\theta })}^k-1]}^{-1/\sigma -1}{(\frac{x}{\theta })}^{{}^{{}^{k-1}}}}{1-e^{-\lambda {[{(\frac{x}{\theta })}^k-1]}^{-1/\sigma }}},$ (2.4)

6cm 6cm

Transformation

Lemma 3.1: If $Y\sim Gu\left(\mu ,\sigma \right)thenX=\theta {(e^Y+1)}^{1/k}\sim GuPdistribution$

The proof is done by using transformation technique.

Quantile function and simulation

The quantile function of Gumbel-Pareto is obtained by inverting (2.2) as$x=Q\left(u\right)=\theta {[1+{(-\frac{1}{\lambda }log u)}^{-\sigma }]}^{1/k}$

 If $u\sim U\left(0,1\right)$ , then X=Q(u) has pdf g(x).

By using Q(u), one can obtain the Galton skewness and Moor’s Kurtosis which is defined as$S=\frac{Q\left(6/8\right)-2Q\left(4/8\right)+Q\left(2/8\right)}{Q\left(6/8\right)-Q\left(2/8\right)}$ $K=\frac{Q\left(7/8\right)-Q\left(5/8\right)+Q\left(3/8\right)-Q\left(1/8\right)}{Q\left(6/8\right)-Q\left(2/8\right)}$

Moments

Theorem 3.1 The $K=\frac{Q\left(7/8\right)-Q\left(5/8\right)+Q\left(3/8\right)-Q\left(1/8\right)}{Q\left(6/8\right)-Q\left(2/8\right)}$ raw moment of Gumbel Pareto distribution is${\mu }_r^{\text{'}}={\theta }^r{\displaystyle {\sum }_{i=0}^{\infty }{\lambda }^{i\sigma }}\left(\begin{array}{l}r/k\hfill \\ i\hfill \end{array}\right)\Gamma \left(1-i\sigma \right)$

 where $\text{Γ}\left(a\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}{t}^{a-1}{e}^{-t}dt}$ is the gamma function.

The skewness and kurtosis can also be calculated from ordinary moments using well-known relationships.

Order Statistics

Order statistics deals with the properties and applications of ordered random samples and their functions. Suppose $X_1,X_2,\mathrm{....}{X}_n$ be a random sample from Gumbel Pareto distribution. Let$X_{r:n}$ denote the $r^{th}$ order statistic. Then the pdf of $X_{r:n}$ can be expressed as

$g_{r:n}\left(x\right)=\frac{n!}{\left(r-1\right)!\left(n-r\right)!}{{\displaystyle \sum _{j=0}^{n-r}\left(-1\right)}}^j\left(\begin{array}{l}n-r\hfill \\ j\hfill \end{array}\right)g\left(x\right)G{(x)}^{j+r-1}$ (3.1)

 Inserting $g\left(x\right)$ and $G\left(x\right)$ in (3.1)and after some algebra we get,$g_{r:n}\left(x\right)={\displaystyle \sum }_{j=0}^{n-r}{\left[\frac{{(-1)}^{j}n!}{\left(r-1\right)!\left(n-r\right)!}\left(\begin{array}{l}n-r\hfill \\ j\hfill \end{array}\right)\frac{\lambda k}{\sigma \theta }[{\left(\frac{x}{\theta }\right)}^k-1\right]}^{-1/\sigma -1}{\left(\frac{x}{\theta }\right)}^{k-1}exp\left\{-\left(r+j\right)(\lambda [\left({\left(\frac{x}{\theta }\right)}^k-1{]}^{-1/\sigma }\right)\right\}$

$={\displaystyle \sum }_{j=0}^{n-r}{\xi }_{j}g\left(x;\lambda ,\sigma ,k,\theta \right)$ (3.2)

 where ${\xi }_j=\frac{{(-1)}^{j}n!}{\left(r-1\right)!\left(n-r\right)!}\left(\begin{array}{l}n-r\hfill \\ j\hfill \end{array}\right)$ and $g\left(x;\lambda ,\sigma ,k,\theta \right)$ is the Gumbel Pareto density function with parameters $\lambda$ ,$\sigma$ , $k$ and $\theta$ .

It reveals that the pdf of Gumbel Pareto order statistics is the mixture of Gumbel Pareto densities.

The maximum likelihood method is applied for estimating the parameters of Gumbel-Pareto distribution. Let $X_1,X_2,\mathrm{....}{X}_n$ be a random sample from Gumbel Pareto(GuP) distribution. Also let $\text{Θ}=\left(\lambda ,\sigma ,k,\theta \right)$ The likelihood function for the GuP distribution is given by$L\left(\Theta \right)={\left(\frac{\lambda k}{\sigma \theta }\right)}^{n}exp\left\{{\left\{-\lambda {\displaystyle {\sum }_{i=1}^n\left[{{\left(\frac{x}{\theta }\right)}^k-1]}^{-1/\sigma }\}{\displaystyle {\prod }_{i=1}^n[{\left(\frac{x}{\theta }\right)}^k-1}\right]}\right\}}^{-1/\sigma -1}{}_{i=1}{}^n\left(\frac{x}{\theta }\right){}^{k-1}\right\}$

 The components of the score vector $U\left(\text{Θ}\right)$ are given by

$U_{\lambda }=\frac{n}{\lambda }-{\displaystyle {\sum }_{i=1}^n{[{(\frac{x_i}{\theta })}^k-1]}^{-1/\sigma }}$

$U_{\sigma }=-\frac{n}{\sigma }-\lambda {\displaystyle {\sum }_{i=1}^n\left\{{\left[{\left(\frac{x_i}{\theta }\right)}^k-1\right]}^{-1/\sigma }\log \left[{\left(\frac{x_i}{\theta }\right)}^k-1\right]\right\}}+\frac{1}{{\sigma }^2}{\displaystyle {\sum }_{i=1}^n\log }\left[{\left(\frac{x_i}{\theta }\right)}^k-1\right]$

$U_k=\frac{n}{k}+\frac{\lambda }{\sigma }{\displaystyle {\sum }_{i=1}^n\left\{{\left[{\left(\frac{x_i}{\theta }\right)}^k-1\right]}^{-1/\sigma -1}{(\frac{x_i}{\theta })}^{k}log\left(\frac{x_i}{\theta }\right)\right\}}+\left(-\frac{1}{\sigma }-1\right){\displaystyle {\sum }_{i=1}^n\frac{\left[{\left(\frac{x_i}{\theta }\right)}^{k}log\left(\frac{x_i}{\theta }\right)\right]}{\left[{\left(\frac{x_i}{\theta }\right)}^k-1\right]}}+nlog\left(\frac{x_i}{\theta }\right)$

$U_{\theta }=-\frac{nk}{\theta }-\frac{\lambda k}{\sigma \theta }{\displaystyle {\sum }_{i=1}^n\left\{{[{\left(\frac{x_i}{\theta }\right)}^k-1]}^{-1/\sigma -1}{\left(\frac{x_i}{\theta }\right)}^k\right\}}+\frac{k}{\theta }\left(\frac{1}{\sigma }+1\right){\displaystyle {\sum }_{i=1}^n\frac{{\left(\frac{x_i}{\theta }\right)}^k}{\left[{\left(\frac{x_i}{\theta }\right)}^k-1\right]}}$

The parameters can be estimated by equating these nonlinear equations to zero and solving them using the nlm function in R program.

In this section, we illustrate the effectiveness of Gumbel - Pareto distribution and compare the results with other existing models. To compare the distributions, we consider standardized goodness of fit measures like $-logL\left(\Theta \right)$ , AIC (Akaike information criterion), CAIC (Consistent Akaike information criterion), BIC (Bayesian information criterion) and HQIC (Hannan - Quinn information criterion). Smaller these values, better is the fit.

Data set I: Number of deaths due to COVID-19 in China. This data is reported in

(https://www.worldometers. info/coronavirus/country/china/) which represents daily deaths due to COVID-19 in China from 23 January to 28 March.

The data are: 8, 16, 15, 24, 26, 26, 38, 43, 46, 45, 57, 64, 65, 73, 73, 86, 89, 97, 108, 97, 146, 121, 143, 142, 105, 98, 136, 114, 118, 109, 97, 150, 71, 52, 29, 44, 47, 35, 42, 31, 38, 31, 30, 28, 27, 22, 17, 22, 11, 7, 13, 10, 14, 13, 11, 8, 3, 7, 6, 9, 7, 4, 6, 5, 3, 5.

Here we compare the new model with Exponentiated tranform of Gumbel type -II model (ETGT -II), Additive Gumbel type II (AGT -II) model and Gumbel type II model. The values of the statistics are given in Table 1.

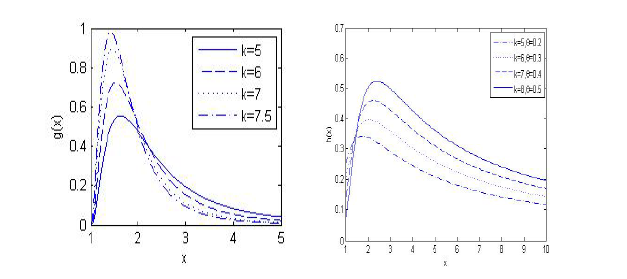
Figure 1 The graph of the pdf and hazard rate of Gumbel - Pareto distribution for various parameter values.

From the table, we can see that the suggested model is suitable for real life applications.

Data set II: The data set is a real data that consists of the number of successive failure for the air conditioning system reported of each member in a fleet of 13 Boeing 720 jet airplanes. The pooled data with 214 observations was considered by Proschan⁷, Kus⁸ and many others. Here we compare the model with existing Weibull Pareto model.

From Table 2, we can see that newly developed Gumbel Pareto distribution is suitable for the given data than the existing Weibull Pareto distribution.²

The reliability is defined as the probability of not failing, denoted by $R$ and is defined as $R=P(X<Y)$ where $X$ represents the stress and represents the strength of a component. For the evaluation of , here we assume that both the random variables follow the distributions belonging to the same family and are independent. There are a number of applications in the literature including stress - strength model and breakdown of a system having two components. If $X$ and $Y$ are two independent random variables with cdf $F_1\left(x\right)$ and $F_2\left(y\right)$ and pdf $f_1\left(x\right)$ and $f_2\left(y\right)$ respectively. Then

$R=P\left(X<Y\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \int }}}{F}_2\left(t\right)f_1\left(t\right)dt.$ (6.1)

Lemma 6.1 If X and Y are two independent random variables following Gumbel - X family of distributions with parameters $\left({\lambda }_1,{\sigma }_1\right)$ and $\left({\lambda }_2,{\sigma }_2\right)$ respectively. Then

$R={\displaystyle {\sum }_{j=0}^{\infty }\frac{{(-1)}^j{\lambda }_2{}^j}{j!{\lambda }_1{}^{\frac{j{\sigma }_1}{{\sigma }_2}}}}\Gamma \left(j\frac{{\sigma }_1}{{\sigma }_2}+1\right)$ (6.2)

 A reliability test plan is developed when the life time of the items follow Gumbel - Pareto distribution. See Jeena and Jose⁹ for more details.^10-14

In this paper, we proposed the new Gumbel-Pareto distribution. We study some of its structural properties including moments, quantile functions and order statistics.The estimation of the model parameters is addressed by maximum likelihood method. We fit the new model to two real data sets to demonstrate the usefulness in practice. We conclude that GuP distribution provides consistently better fit than other competing models for the data set. We hope that the proposed model will attract wider applications in various areas such as engineering, survival and lifetime data, hydrology,economics, Biostatistical data on Cancer, Covid etc

1. Al - Aqtash R. On generating a new family of distributions using the logit function. Ph.D. thesis, central michigan university, mount pleasant, michigan. 2013.
2. Alzaatreh A, Lee C, Famoye F. A new method for generating families of continuous distributions. Metron. 2013a;71(1):63‒79.
3. Alzaatreh A, Lee C, Famoye F. Weibull pareto distribution and its applications. Communications in statistics - theory and methods. 2013b; 42(9): 1673‒1691.
4. Yoo K, Arashi M, Bekker A. Pitting the Gumbel and logistic growth models against one another to model COVID-19 spread. medRxiv. 2020.
5. Sindhu TN, Shafiq A, Al-Mdallal QM. Exponentiated transformation of Gumbel Type-II distribution for modeling COVID-19 data. Alexandria Engineering Journal. 2021;60(1):671‒689.
6. Kocha Åczyk M, Lipniacki T. Pareto-based evaluation of national responses to COVID-19 pandemic shows that saving lives and protecting economy are non-trade-off objectives. Scientific reports. 2021;11(1):1‒9.
7. Proschan F. Theoretical explanation of observed decreasing failure rate. Technometrics. 1963;5(3):375‒383.
8. Kus C. A New lifetime distribution. Computational statistics and data analysis. 2007;51(9):4497‒4509.
9. Joseph J, Jose KK. Reliability test plan for gumbel–pareto life time model. International Journal of Statistics and Reliability Engineering. 2021;8(1):121‒131.
10. Beare BK, Toda. On the emergence of a power law in the distribution of COVID-19 cases. Physica D: Nonlinear Phenomena. 2020;412:132649.
11. EJ Gumbel. Statistical theory of extreme values and some practical applications. Applied Mathematics, 1st edn. vol. 33, U.S. Department of Commerce, National Bureau of Standards, ASIN B0007DSHG4, Gaithersburg, Md, USA. 1954.
12. Kotz S, Nadarajah S. Extreme value distributions: theory and applications. Imperial College Press, London. 2000.
13. S Nadarajah. The exponentiated Gumbel distribution with climate application, Environmetrics. 2006;17(1):13‒23.
14. Wong F, Collins JJ. Evidence that coronavirus superspreading is fat-tailed. Proceedings of the national academy of sciences. 2020;117(47):29416‒29418.