Growth in reading comprehension and mathematics achievement in primary school: a bivariate transition multilevel growth curve model approach

doi:10.15406/bbij.2017.05.00137

eISSN: 2378-315X

Biometrics & Biostatistics International Journal

Research Article Volume 5 Issue 4

Growth in reading comprehension and mathematics achievement in primary school: a bivariate transition multilevel growth curve model approach

Dickson Nkafu Anumendem,¹

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Bieke De Fraine,¹ Patrick Onghena,² Jan Van Damme³

¹Centre for Educational Effectiveness and Evaluation of the Katholieke Universiteit Leuven, Belgium
²Centre for Methodology in Educational Sciences of the Katholieke Universiteit Leuven, Belgium
³Centre for Educational Effectiveness and Evaluation, both at the Katholieke Universiteit, Belgium

Correspondence: Nkafu Dickson Anumendem, Centre for Educational Effectiveness and Evaluation of the Katholieke Universiteit Leuven, Dekenstraat 2 / 3773, 3000 Leuven, Belgium, Tel 32-163-257-75

Received: August 08, 2016 | Published: March 28, 2017

Citation: Anumendem DN. Growth in reading comprehension and mathematics achievement in primary school: a bivariate transition multilevel growth curve model approach. Biom Biostat Int J. 2017;5(4):112-123. DOI: 10.15406/bbij.2017.05.00137

Download PDF

Introducton

The measurement and explanation of school effects on both students’ reading comprehension and mathematics achievement in primary school children has seldom been studied. Some studies have focused on mathematics achievement as a predictor of reading comprehension¹ or reading as a predictor of mathematics performance.² These studies make the key assumption of deciding in advance which of the outcomes is dependent on the other. A few multivariate studies have nonetheless been done to investigate the possibility of a relationship between overall reading ability and mathematics, by looking at the common characteristics responsible for high performance in mathematics and reading (e.g. De Maeyer et al.³ The current study goes further, because it investigates growth in reading comprehension and mathematics without any assumption on their functional dependence. The call for the use of multivariate methods to investigate the strength of a relationship between outcomes has been an invaluable problem in educational research as a whole.^4,5

Reading achievement in primary school contains two distinguishable components: word reading and reading comprehension. Reading comprehension is a complex process and requires not only the fluent decoding of words but also understanding vocabulary, making inferences and relating the ideas to prior knowledge. Reading comprehension in primary schools stretches from the understanding of the meaning of words to the meaning of a short text and this is highly dependent on age. Many researchers have argued that true measurement of reading comprehension skills can only be obtained at later stages of primary school say from the third grade on (7 or 8 years old).^6-8 This paper focuses on reading comprehension which requires more advanced cognitive and linguistic skills. For this reason pupils were only tested from the end of grade 3 on. While studies have shown that individual differences in reading comprehension in particular during primary school are stable,⁹ differences between schools¹⁰ however have not been addressed in depth. It might also be interesting to find out if this stability mentioned by (De Jong and Van Der Leij⁹) remains when considered in conjunction with mathematics.

Mathematics achievement in primary schools usually embodies different components like: arithmetic, basic number knowledge, memorisation of arithmetic operations like addition, subtraction, and conceptual understanding and procedural knowledge.^11,12 Studies have shown that pupils’ skill in mathematics develops rapidly during formal instruction.^13,14

Most studies in the field of educational effectiveness are limited to only one outcome variable as the effectiveness criterion. Or these studies report on several effectiveness criteria, but they model each criterion separately. Many researchers have called for the development of better statistical methods capable of handling more than one effectiveness criterion in the same model.^10,15,16 When effectiveness criteria are modelled separately, the underlying assumption is that these different effectiveness criteria are independent of each other. As far as the school effects estimation is concerned, we hypothesize that this assumption is most often not tenable with reading comprehension and mathematics in primary school. The implication of such an assumption is for example, that a pupil’s or school’s score in mathematics is not related to the pupil’s or school’s performance in reading comprehension. On the contrary, some studies have suggested that mathematics achievement and reading as a whole may depend on similar predictors,^17,18 strengthening the need for combining these effectiveness criteria. Other studies have even found that similar linguistic abilities are needed for both mathematics problem solving and reading comprehension tasks.¹⁹ Further studies have identified four components of mathematical problem solving as; translation, integration, solution planning and execution, with the first two of these components highly correlated with reading comprehension skills.²⁰

In addition to the plea for multiple criteria, educational effectiveness researchers advocate studying student outcomes over time.^21–23 It is argued that growth in student outcomes over time is a very essential criterion since learning means changing.¹⁰ In order to investigate changes in student outcomes over time, longitudinal data are invaluable. This paper will address both the plea for multiple effectiveness criteria and the plea for studying growth. The use of growth curves as a statistical method introduces another level of choice of criterion beyond the choice of pupil outcome variable. This paper tries in the next section to delineate these two stages of school effectiveness criteria. Firstly, the choice of the dependent or outcome variables with a correlation strong enough to lend credence to a multivariate model instead of separate univariate models. Secondly, one has to make a choice of which growth curve parameters to use to model the student outcomes and to estimate the school effect. These parameters could be obtained at a certain point in time (intercept) or as a growth parameter (linear or quadratic). A bivariate transition multilevel growth curve model (BTMGCM) is introduced in this paper as a way of circumventing the problem of missing reading comprehension scores at the early grades.

Two-stage effectiveness criteria

Generalisation of results of different studies with different criteria has most often been problematic given that school effects are only moderately consistent over different criteria. Moreover, the consistency issue has seldom been studied through growth curve models. This paper introduces what is called “two-stage effectiveness criteria” to study school effect consistency in multivariate multilevel growth curve models (MMGCM). In stage 1, the researcher chooses one or more student outcomes (reading comprehension, mathematics achievement, well-being, etc.) and in stage 2, the growth parameters are chosen (initial status, linear change, quadratic slope, etc.). This process can result in two or more effectiveness criteria depending on the number of outcome variables and the nature of the growth. For example, two outcome variables and a random intercept and linear growth model will have four possible effectiveness criteria: an intercept (student status) and a linear slope (student growth) each for both outcomes. It is important to note that this two-stage effectiveness criteria is not limited to educational effectiveness research but can adequately be applied to other educational research domains as long as the researcher has a good longitudinal data on more than one outcome of interest.

The current study has two first stage criteria which are mathematics and reading comprehension and two second stage criteria (intercept and linear slope). The four effectiveness criteria in this study are therefore: mathematics intercept, mathematics slope, reading comprehension intercept and reading comprehension slope. These four effectiveness criteria (Figure 1- illustrate pupils' growth in both mathematics and reading comprehension (and their relation) in primary schools through a bivariate multilevel growth curve model (BMGCM).

Figure 1 A proposed schema of the two-stage school effectiveness criteria for a bivariate linear growth curve model.

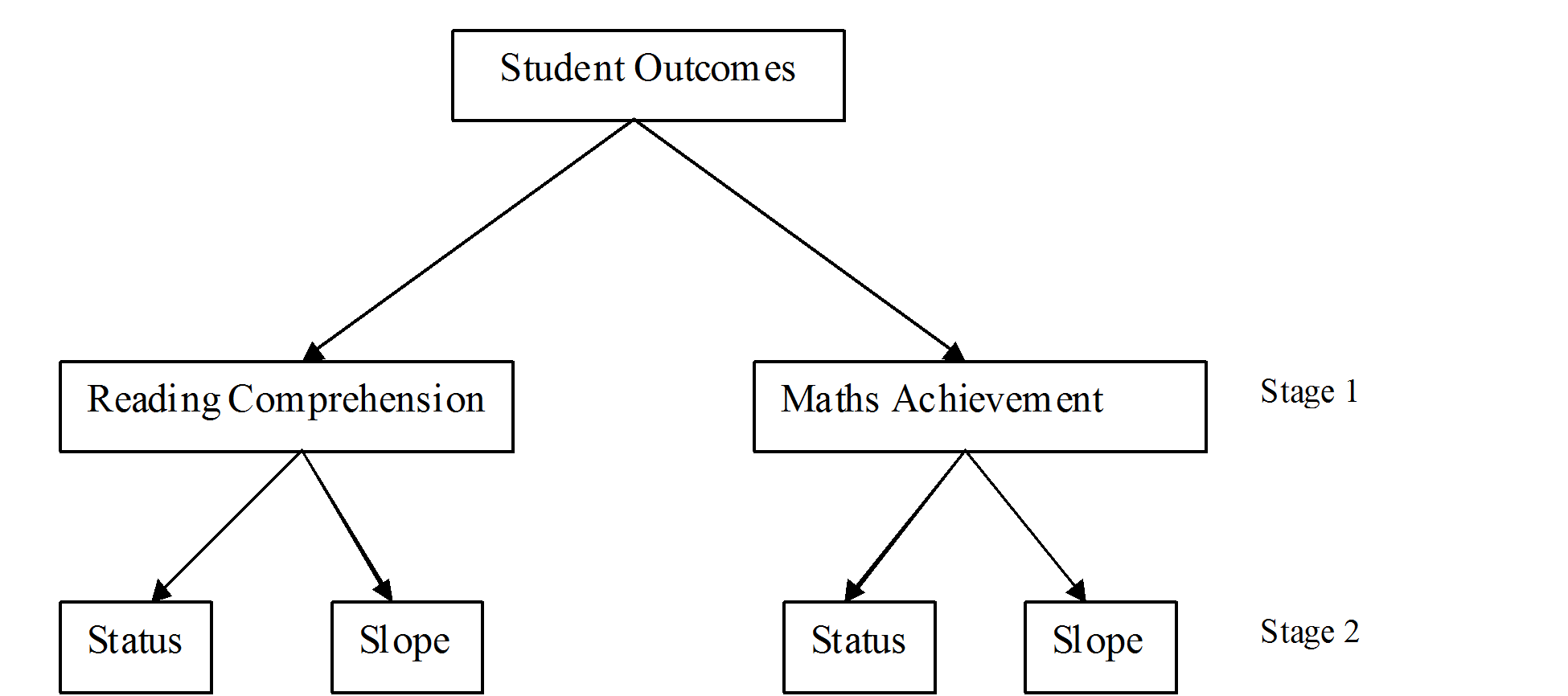
The advantages of MMGCM are enormous. They are not only statistically powerful, but are also capable of answering a wider range of research questions more efficiently. These questions could stretch from stability to consistency of school effects. The choice of characteristics taking into account their dependence, can greatly reduce the chance of making a type 1 error (Hox, 2002) and as a consequence, improves generalisability of the study findings. The use of MMGCM is not limited to the investigation of cognitive outcomes but all non-cognitive outcomes and a mix of both. Some researchers have used a latent growth approach to looked into the relationship between two students’ outcomes, academic self-concept and language achievement.^21,24

Objectives

The main objectives of the current study are summarised by the following research questions:

What is the nature of the evolution of mathematics achievement and reading comprehension from the end of Grade 3 to the end of Grade 6 in primary school? Are there differences in the growth trajectories for these two outcomes?
What is the correlation between the mathematics and reading comprehension growth profiles at the pupil level and at the school level?
How large is the school effect on the pupil status and pupil growth? Is this effect similar for the two outcomes?
What is the impact on the estimates of the school effects when the dependence of mathematics and reading comprehension is taken into account? In other words, we will compare school effects for two separate univariate models and one bivariate model.
Can the prior growth in mathematics explain the subsequent differences in pupils’ status and growth in reading comprehension and mathematics achievement?

Methodology

In this section, we will discuss three models: (Model 1) the univariate multilevel growth curve model (UMGCM), (Model 2) the bivariate multilevel growth curve model (BMGCM) and (Model 3) the extension to a transition model (the bivariate transition multilevel growth curve model, BTMGCM). Model 1 will be used to answer the first research question, while model 2 will be used to tackle the second and third research questions. Research question four is based on the comparison of the results based on the Model 1 and 2. The last research question is then handled with model 3.

Univariate multilevel growth curve model (UMGCM)

The univariate multilevel growth curve models (UMGCM) will be applied to the mathematics scores on the one hand and the reading comprehension scores on the other hand. These two univariate multilevel growth curve models are each of the form

$y_{i} | b_{i} ~ N (X_{i} β + Z_{i} b_{i}, Σ_{i})$ (1)

In equation 1 above, the $y_{i}$ ’ s are vectors representing all the measurements for the $i^{t h}$ school.

Each outcome or response measurement $Y = (Y_{1}, Y_{2})$ denotes the $k^{t h}$ measurement for the $j^{t h}$ student from the $i^{t h}$ school. This means the vector of responses

$y_{i}$ = ( $y_{i 11}$ , $y_{i 12}$ ,…, $y_{i 1 m_{j}}$ ,…, $y_{i n_{i} m_{j}}$ )T.

Bivariate multilevel growth curve model (BMGCM)

In the bivariate model, the two outcomes are combined through the proper specifications of a bivariate distribution for all the random effects taking into account the dependence of the growth processes. In this combined model, a bivariate normally distributed response is considered for the new response Y. Where $Y = (Y_{1}, Y_{2})$ $N ((X_{1} β {}_{1}, X_{2} β_{2}), (Σ_{1}, Σ_{2}))$ and the mean structures, variance matrices that are allowed to be different and an extra covariance component as explained later on.

A multivariate response can be incorporated into a multilevel growth curve model by creating an extra lowest level, which is called level zero in this paper. In the growth curve model setting, the two responses are nested within the measurement occasions which are in turn nested within the students and finally within the schools. The main purpose of the level 0 is to define the double response per pupil. Our interest is then to use this model to assess the relationship between the growth parameters of the two response variables (reading comprehension and mathematics achievement) Figure 2.

Figure 2 Data collection structure for reading comprehension and mathematics outcome variables.

Modelling the two outcome variables simultaneously, accounts for the dependence between the outcomes and thus improves the parameter estimates of the model. This is usually of great importance when association structures change with time.²⁵ In this study, we will fit a model, which has a structure of a four-level model but with the lowest level called level 0 because its variability is not of interest. The reason being that the level 0 index is used only to differentiate between the response variables. In this case the structure of the data fits into a multilevel growth curve model.

$\begin{array}{l} Y_{i j k} = β_{01} z_{1 i j k} + β_{02} z_{2 i j k} + β_{11} t_{_{i j k}}^{} z_{1 i j k} + β_{12} t_{_{i j k}}^{} z_{2 i j k} + β_{21} t_{_{i j k}}^{2} z_{1 i j k} + β_{22} t_{_{i j k}}^{2} z_{2 i j k} + \\ (v_{00 k} + v_{10 k} t_{_{i j k}}^{} + v_{20 k} t_{_{i j k}}^{2} + u_{0 i k} + u_{1 i k} t_{_{i j k}}^{} + u_{2 i k} t_{_{i j k}}^{2} + ε_{i j k}) z_{1 i j k} + \\ (v'_{00 k} + v'_{10 k} t_{_{i j k}}^{} + v'_{20 k} t_{_{i j k}}^{2} + u'_{0 i k} + u'_{1 i k} t_{_{i j k}}^{} + u'_{2 i k} t_{_{i j k}}^{2} + ε'_{i j k}) z_{2 i j k} \end{array}}$ (2)

where $\begin{array}{l} z_{1 i j k} = {\begin{matrix} 1 i f R e a d i n g c o m p r e h e n s i o n \\ 0 i f M a t h e m a t i c s a c h i e v e m e n t \end{matrix} \\ z_{2 i j k} = {\begin{matrix} 0 i f R e a d i n g c o m p r e h e n s i o n \\ 1 i f M a t h e m a t i c s a c h i e v e m e n t \end{matrix} \end{array}$

This means our model can be written as

$Y_{i j k} = {\begin{matrix} β_{01} + β_{11} t_{_{i j k}}^{} + β_{21} t_{_{i j k}}^{2} + v_{00 k} + v_{10 k} t_{_{i j k}}^{} + v_{20 k} t_{_{i j k}}^{2} + u_{0 i k} + u_{1 i k} t_{_{i j k}}^{} + u_{2 i k} t_{_{i j k}}^{2} + ε_{i j k} i f z_{1 i j k} = 1 \\ β_{02} + β_{12} t_{_{i j k}}^{} + β_{22} t_{_{i j k}}^{2} + v'_{00 k} + v'_{10 k} t_{_{i j k}}^{} + v'_{20 k} t_{_{i j k}}^{2} + u'_{0 i k} + u'_{1 i k} t_{_{i j k}}^{} + u'_{2 i k} t_{_{i j k}}^{2} + ε'_{i j k} i f z_{2 i j k} = 1 \end{matrix}$

The school level variance (level 3) is given by:

$(\begin{matrix} v_{00 k} \\ v_{10 k} \\ v_{20 k} \\ v'_{00 k} \\ v'_{10 k} \\ v'_{20 k} \end{matrix}) ~ M V N ((\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}), (\begin{matrix} σ_{v_{0}}^{2} \\ σ_{v_{1} v_{0}}^{} & σ_{v_{1}}^{2} \\ σ_{v_{2} v_{0}}^{} & σ_{v_{2} v_{1}}^{} & σ_{v_{2}}^{2} \\ σ_{v'_{0} v_{0}}^{} & σ_{v'_{0} v_{1}}^{} & σ_{v'_{0} v_{2}}^{} & σ_{v'_{0}}^{2} \\ σ_{v'_{1} v_{0}}^{} & σ_{v'_{1} v_{1}}^{} & σ_{v'_{1} v_{2}}^{} & σ_{v'_{1} v'_{0}}^{} & σ_{v'_{1}}^{2} \\ σ_{v'_{2} v_{0}}^{} & σ_{v'_{2} v_{1}}^{} & σ_{v'_{2} v_{2}}^{} & σ_{v'_{2} v'_{0}}^{} & σ_{v'_{2} v'_{1}}^{} & σ_{v'_{2}}^{2} \end{matrix}))$ ,

and for the student level variance (level 2):

$(\begin{matrix} u_{0 j k} \\ u_{1 j k} \\ u_{2 j k} \\ u'_{0 j k} \\ u'_{1 j k} \\ u'_{2 j k} \end{matrix}) ~ M V N ((\begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{matrix}), (\begin{matrix} σ_{u_{0}}^{2} \\ σ_{u_{1} u_{0}}^{} & σ_{u_{1}}^{2} \\ σ_{u_{2} u_{0}}^{} & σ_{u_{2} u_{1}}^{} & σ_{u_{2}}^{2} \\ σ_{u'_{0} u_{0}}^{} & σ_{u'_{0} u_{1}}^{} & σ_{u'_{0} u_{2}}^{} & σ_{u'_{0}}^{2} \\ σ_{u'_{1} u_{0}}^{} & σ_{u'_{1} u_{1}}^{} & σ_{u'_{1} u_{2}}^{} & σ_{u'_{1} u'_{0}}^{} & σ_{u'_{1}}^{2} \\ σ_{u'_{2} u_{0}}^{} & σ_{u'_{2} u_{1}}^{} & σ_{u'_{2} u_{2}}^{} & σ_{u'_{2} u'_{0}}^{} & σ_{u'_{2} u'_{1}}^{} & σ_{u'_{2}}^{2} \end{matrix}))$ .

The level 1 matrix components represent parameters associated with the error terms of the two growth processes

$(\begin{matrix} ε_{i j k} \\ ε_{i j k'} \end{matrix}) ~ M V N ((\begin{matrix} 0 \\ 0 \end{matrix}), (\begin{matrix} σ_{1}^{2} \\ σ_{21} & σ_{2}^{2} \end{matrix}))$

In vector notation we can simple write
$ν_{k} ~ M V N (0, Ω_{v}), υ_{j k} ~ M V N (0, Ω_{u}) a n d ε_{i j k} ~ M V N (0, Ω_{ε})$

Where $0$ is a zero mean vector and $Ω_{v}$ and $Ω_{u}$ are respectively the covariance matrices for the school and student levels. An extension of this unconditional growth curve model to a conditional model is possible. A conditional growth curve model will include other covariates in addition to time.²⁶ Conditional versions of the BMGCM can enable the estimation of general and specific effects for the combined responses or for each response in the model respectively. A quadratic growth model is presented above for completeness making it easier for the reader to follow a less complex application of its linear growth equivalent.

Bivariate transition multilevel growth curve model (BTMGCM)

A common problem with multivariate outcome data is the possibility of incomplete observations in the outcome vector. There are a number of reasons why some observations might be absent in a study. When incomplete observations are missing at random or even completely at random, maximum likelihood estimates obtained from multilevel growth curve models²⁷ or the full maximum likelihood estimates for latent growth models,²⁴ are still valid. However sometimes because of the design of the study, the statistical method used or the type of pupil outcomes to be considered, attritions occur in one outcome variable and not in the other. The situation in this study is summarized in Table 1 with the (X) indicating that a test was administered at that primary school grade. Students took a mathematics test at 7 occasions, while the reading comprehension test was administered at 4 occasions.

Outcome	Begin grade1	End grade1	End grade2	End grade3	End grade4	End grade5	End grade6
Mathematics	X	X	X	X	X	X	X
Reading Comp				X	X	X	X

Table 1 Overview of the measurement occasions of the mathematics and reading comprehension tests

A bivariate transition multilevel growth curve model (BTMGCM) is introduced in this section as a way of circumventing the problem of missing reading comprehension scores at the beginning of grade 1, end of grades 1 and 2. This is considered as a better alternative to deleting the available mathematics scores obtained at those measurement occasions. The purpose of this model is to account for any possible dependence of the pupils reading comprehension and mathematics growth curves on these prior mathematics achievement scores.

Transition models are a specific class of conditional models. In a transition model, an outcome ( $Y_{i j k}$ ) in a longitudinal sequence is described as a function of previous outcomes or history $h_{i j k}$ = ( $Y_{i j 1}$ ,…, $Y_{i j k - 1}$ ).^28,29 The order of a transition model is the number of previous measurements that is still considered to influence the current outcome. This is a model which is simple to fit and understand yet strong enough to enable the investigation of the complex relationship that current processes have with their history. These models have been discussed in detail in textbooks such as Diggle et al.,²⁸ Molenberghs and Verbeke³⁰ and Fahrmeir and Tutz.²⁹ However, extensions to handle more than one student outcome and in a multilevel growth curve model setting have never been done. It is in this context that the following BTMGCM is introduced, firstly, to solve the problem of unequal number of measurement occasions for the two pupil outcomes. And secondly, the model provides a powerful framework that can throw more light on the question of dependence of growth in one outcome on previous growth in a different outcome. The formulation of a bivariate transition model is given as follows:

$Y_{i j k} = {\begin{matrix} β_{01} + β_{11} t_{_{i j k}}^{} + β_{21} t_{_{i j k}}^{2} + κ_{1} (h_{i j k}, β) + v_{00 k} + v_{10 k} t_{_{i j k}}^{} + v_{20 k} t_{_{i j k}}^{2} + u_{0 i k} + u_{1 i k} t_{_{i j k}}^{} + u_{2 i k} t_{_{i j k}}^{2} + ε_{i j k} i f z_{1 i j k} = 1 \\ β_{02} + β_{12} t_{_{i j k}}^{} + β_{22} t_{_{i j k}}^{2} + κ_{2} (h_{i j k}, β) + v'_{00 k} + v'_{10 k} t_{_{i j k}}^{} + v'_{20 k} t_{_{i j k}}^{2} + u'_{0 i k} + u'_{1 i k} t_{_{i j k}}^{} + u'_{2 i k} t_{_{i j k}}^{2} + ε'_{i j k} i f z_{2 i j k} = 1 \end{matrix}$

Where $κ_{1}$ , $κ_{2}$ are functions (most often linear) of the history ( $h_{i j k}$ ). In the special case of this study where the history for both outcome variables is based on the first three time point measurements of mathematics, $κ_{1} = κ_{〈 2 〉} = κ_{}$ . The $β$ ’s indicate the possibility of separate models for the independent variables of the growth curve model. In compact form, the bivariate transitional growth curve model can be written as

$y_{i} | (b_{i}, κ (h_{i}, β)) ~ N (X_{i} β + Z_{_{i}} b_{i} + κ (h_{i}, β), Σ_{i})$ .

The next section proceeds with the application of the models described so far. First of all the paper examines if BMGCMs are more realistic and statistically backed to use instead of two separate UMGCMs. Next it compares the BMGCM with the bivariate growth model controlling for previous changes in mathematics using BTMGCM. The results from the three models are then investigated for any fundamental changes in the conclusions.

Application

The data used for this study were collected as part of a longitudinal research project to describe and explain pathways through primary education, SiBO (Schoolloopbanen Inhet Basis Onderwijs). There were about 200 Flemish schools that participated in this study, which started in September 2003 and followed one cohort of pupils throughout their career in primary school (Grade 1 to Grade 6). All the pupils took mathematics achievement tests at 7 occasions and reading comprehension tests (Dutch language) at four occasions (see previous section). Grade-appropriate tests with common scales for the reading comprehension and mathematics scores were obtained separately for four measurement occasions and seven measurement occasions respectively, using Item Response Theory. A number of background variables were also collected including: socio-economic status of the family, gender, language spoken at home, age and ethnic-cultural background. The sample used for this paper had 194 schools with 6250 pupils.

The average growth profile was explored for both mathematics and reading comprehension and looking at the deviance statistics and parsimony, we settled down to a linear growth model for both outcomes. The time variable (linear slope) is coded 0 for end of Grade 3, 1 for end of Grade 4, 2 for end of Grade 5 and 3 for end of Grade 6. This means the intercept (student status) is considered at the end of Grade 3. Two main software programmes are used in this study because of their different merits. First, SAS 9.1 (SAS Institute Inc., 2003) is used because of its PROC MIXED which is very flexible and suitable for fitting hierarchical linear models and growth curve models (Singer, 1998). Secondly, MLwiN 2.02³¹ provides a wide range of multilevel models together with plotting diagnostics. Alternative software like³² could equally be used to fit some of the models described in this paper.

Results

The results of the BMGCM reveal interesting improvements in the estimates of school effects and correlations in comparison with UMGCMs. First and foremost, the level-1 correlation for the joint growth processes for mathematics and reading comprehension is 0.17 and significant at a 5% level (p < 0.0001) indicating the need of fitting a bivariate model instead of two separate univariate models to the data.

Looking at the results of the first column of Table 2a for the student level of the UMGCM, it is clear that all the variance-covariance parameters are significant except for the covariance between the pupil’s status and growth in reading comprehension. This seems to indicate that the pupils’ level for reading comprehension at the end of grade 3 has no significant relationship with the pupils’ growth thereafter. However, the negative correlation between the pupils’ status in mathematics and growth in mathematics (-0.182) is significant at a 5% level. Pupils with a high mathematics score at the end of grade 3 generally grow less between the end of grade 3 and end of grade 6.

The second column of Table 2a shows the results of the BMGCM with four extra parameters rendering the possibility to answer many more research questions. The non-significant correlation between pupils’ status and growth in reading comprehension for the UMGCM is now significant under the BMGCM with value -0.085. This correlation is in the same direction as that between pupils’ mathematics status and growth though weaker. Also the effect of pupils’ status on growth in mathematics is significant and seems stronger in the BMGCM (-0.222) than in the UMGCM (-0.182). The cross co-variances were all significant with corresponding correlations of 0.691 between pupils’ mathematics intercept and reading comprehension intercept. Pupils with high scores in mathematics also tend to have high scores in reading comprehension at the end of grade 3.

Another positive correlation of 0.162 was observed between the pupils’ mathematics intercept and reading comprehension slope. This means the pupils with a high score in mathematics at the end of grade 3 tend to grow faster in reading comprehension subsequently. A correlation of 0.391 is estimated between pupils’ mathematics slope and reading comprehension slope. This indicates that fast growing pupils in mathematics also grew fast for reading comprehension. There is a significant and negative correlation for the pupils’ reading comprehension intercept and slope in mathematics (-0.095). The negative correlation means that high achievers in reading comprehension at the end of grade 3 generally had a slower growth in mathematics.

The results for the school level presented in Table 2b show some positive and significant correlations between the average mathematics and reading comprehension intercepts (0.672) and between their slopes (0.581). Schools with high end of year 3 scores in mathematics also have high scores in reading comprehension. Similarly schools with a steeper average slope in mathematics turn to have a steeper slope in reading comprehension too. The Table 2b results also show negative and significant correlations between the average intercept and average growth of schools for both mathematics and reading comprehension of -0.301 and -0.246 respectively. This means that schools with a high average mathematics score at the end of year 3 tend to have a slower average growth in mathematics during the subsequent grades, and so do the schools with high average reading comprehension. There were two correlations not significant at the 5% level for the relationship between schools’ average intercept in mathematics and average growth in reading comprehension and between the schools’ average intercept in reading comprehension and average growth in mathematics. These results may suggest that the school average growth in mathematics is not influenced by the average reading comprehension at the end of grade 3 and that the growth in reading comprehension is not influenced by the mathematics status too.

Variance parameter	UMGCM			BMGCM
Variance parameter	Estimate	Std error	Correlation	Estimate	Std error		Correlation
Math status	57.783	1.254	1	67.629	1.435	1
Math slope	1.058	0.081	1	0.594	0.087	1
Read status	36.926	0.879	1	47.184	1.038	1
Read slope	0.861	0.081	1	0.888	0.083	1
Covariance parameter
Math status - slope	-1.425	0.251	-0.182	-1.408	0.293	-0.222
Read status - slope	-0.325	0.205	0.058	-0.555	0.243	-0.086
Math status - Read status	/	/		39.025	1.011	0.691
Math status - Read slope	/	/		1.255	0.279	0.162
Math slope - Read status	/	/		-0.501	0.263	-0.095
Math slope - Read slope	/	/		0.284	0.062	0.391

a) Student level variance parameters
Estimates in bold are not significant at a 5% level using a Wald test. Mat=mathematics, Read=reading comprehension, status is the student intercept at the end of grade 3 and slope= linear growth.

Variance parameter	UMGCM			BMGCM
Variance parameter	Estimate	Std error	Correlation	Estimate	Std error	Correlation
Math status	17.853	2.121	1	15.44	1.917	1
Math slope	0.961	0.121	1	1.079	0.137	1
Read status	14.044	1.655	1	12.373	1.508	1
Read slope	0.456	0.068	1	0.676	0.093	1
Covariance parameter
Math status - slope	-1.665	0.39	-0.402	-1.231	0.383	-0.302
Read status - slope	-0.681	0.249	-0.269	-0.712	0.274	-0.246
Math status - Read status	/	/		9.277	1.439	0.671
Math status - Read slope	/	/		-0.05	0.299	-0.015
Math slope - Read status	/	/		-0.474	0.325	-0.13
Math slope - Read slope	/	/		0.497	0.09	0.582

b) School level variance parameters
Estimates in bold are not significant at a 5% level using a Wald test. Mat=mathematics, Read=reading comprehension, status is the student intercept at the end of grade 3 and slope= linear growth.

Table 2 Random Effects of the univariate multilevel growth curve models (UMGCM) compared with the bivariate multilevel growth curve model (BMGCM) with 4 measurements for Mathematics and Reading Comprehension

After considering that a bivariate growth model was the better model compared with two separate univariate growth models, the bivariate transition growth model was fitted to handle the difference in number of measurement occasions for reading comprehension and mathematics. The bivariate transition multilevel growth curve model (BTMGCM) is suggested in this study not only to solve inequality in the number of measurement occasions between the two outcome variables but also as a means of answering the fifth research question of the current study. In this special design of the transition model, the previous measurement covariates are constructed as changes in the mathematics achievement of the pupils between the beginning and end of first grade and between the end of grade 1 and the end of grade 2. Two such second order transition growth models are fitted. The BTMGCM (I) includes the two covariates (math2_1 and math3_2) as main effects only and the BTMGCM (II) adds the interactions between the two covariates and the time variable.

$E (Y_{i j k}) = {\begin{matrix} β_{01} + β_{11} t_{_{i j k}}^{} + α_{10} m a t h 2_1 + α_{11} m a t h 3 - 2 + α_{12} m a t h 2_1 * t_{_{i j k}}^{} + α_{13} m a t h 3_2 * t_{_{i j k}}^{} i f z_{1 i j k} = 1 \\ β_{02} + β_{12} t_{_{i j k}}^{} + α_{20} m a t h 2_1 + α_{21} m a t h 3_2 + α_{22} m a t h 2_1 * t_{_{i j k}}^{} + α_{23} m a t h 3_2 * t_{_{i j k}}^{} i f z_{2 i j k} = 1 \end{matrix}$

Estimates bold are not significant at a 5% level. Math2_1=change in mathematics between start of grade 1 and end of grade 1, Math3_2= change in mathematics between end of grade 1 and end of grade 2. Reading Comp=reading comprehension, status is the student intercept at the end of grade 3.

The results of Table 3 show quite some differences between the fixed effects estimates of the BMGCM and the two versions of the BTMGCM. The BTMGCM (I) considers the dependence on the main effects of the two previous growths in mathematics (Math2_1 and Math3_2) and BTMGCM (II) also includes the interaction effect of these previous changes with time. The deviance statistics can be used to compare the fits of the models using the difference in the log likelihood values and difference in degrees of freedom and a chi-square distribution as the null distribution for the likelihood ratio test statistic. Comparing BMGCM and BTMGCM (I) indicate a deviance value of 49506.3 with only 4 degrees of freedom is very significant (p < 0.0001) indicating that there will be a significant loss in information by trying to reduce the BTMGCM (I) to BMGCM. A similar conclusion is established between BTMGCM (I) and BTMGCM (II) in favour of BTMGCM (II) (p-value =0.017). The estimates of the earlier prior change in mathematics (start and end of grade 1) affect the pupils’ growth in both reading comprehension and mathematics from the end of grade 3 to the end of grade 6. On the other hand the later prior change in mathematics (between end of grade 1 and end of grade 2) seems to impact only the pupils’ subsequent growth in reading comprehension not their growth in mathematics.

Fixed effects parameter	BMGCM	BTMGCM (I)	BTMGCM (II)
Fixed effects parameter	Estimate (std error)	Estimate (std error)	Estimate (std error)
Intercept Reading Comp	43.224 (0.245)	46.051(0.362)	46.633 (0.395)
Intercept Mathematics	90.571 (0.312)	88.809 (0.479)	88.884 (0.497)
Time*Reading Comp	5.249 (0.068)	5.305 (0.071)	4.518 (0.135)
Time*Mathematics	5.563 (0.082)	5.584 (0.087)	5.248 (0.144)
Math2_1*Reading Comp	/	-0.145 (0.017)	-0.168 (0.017)
Math2_1*Mathematics	/	0.066 (0.019)	0.055 (0.018)
Math3_2*Reading Comp	/	-0.014 (0.019)	-0.039 (0.018)
Math3_2*Mathematics	/	0.179 (0.021)	0.185 (0.022)
Math2_1TimeRead Comp	/	/	0.030 (0.005)
Math2_1TimeMathematics	/	/	0.018 (0.005)
Math3_2Time Read Comp	/	/	0.033 (0.005)
Math3_2TimeMathematics	/	/	0.008 (0.006)
-2loglikelihood	238524.3	189018.9	189005.5
Degrees of freedom	28	32	36

Table 3 Comparing the fixed effects estimates and model fits of a bivariate multilevel growth curve model (BMGCM) and two bivariate transitional multilevel growth curve models (BTMGCM (I) and BTMGCM (II))

Estimates in bold are not significant at a 5% level. Math2_1=change in mathematics between start of grade 1 and end of grade 1, Math3_2= change in mathematics between end of grade 1 and end of grade 2. Reading Comp=reading comprehension, status is the student intercept at the end of grade 3.

A summary of the fixed effects result is presented as growth profiles for the UMGCM, BMGCM and the final bivariate transition growth curve model in Figure 3. The graphs of Figure 3(a) reveal that the average pupil score in reading comprehension at the end of grade 3 is underestimated by the univariate model (Read UMGCM) and improved by the bivariate model (Read BMGCM). In any case, the BTMGCM (for pupils with 1SD difference in prior math achievement (ReadBTMGCM+1SD) for both Math2_1 and Math3_2), gives the largest estimates for the reading comprehension score at the end of grade 3. A possible explanation for the underestimation by the UMGCM and BMGCM is that these models assume falsely that the growth processes only started at the end of grade 3. The BTMGCM (II) seems to indicate that growth in mathematics of the previous grades has a role to play in the average reading comprehension performance of pupils at the end of the third grade.

The graphs of Figure 3(b) show no big difference between the BMGCM and BTMGCM for their estimates of the average score in mathematics at the end of grade 3. This means that the change in prior mathematics achievement has a bigger influence on pupils’ subsequent development in reading comprehension than in mathematics.

Figure 3 Average growth profiles for the UMGCM, BMGCM and BTMGCM (for +1SD difference in prior change) a) reading comprehension and b) mathematics.

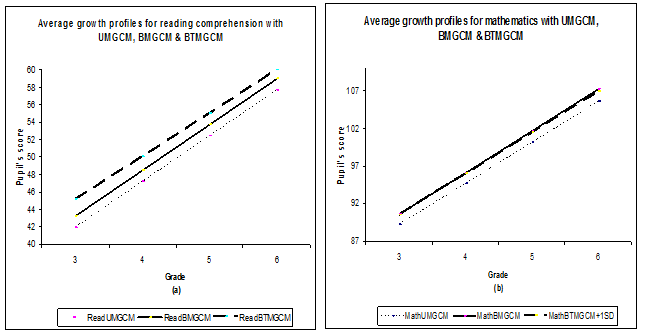
Also the growth in pupils’ reading comprehension is larger in the BMGCM probably because this model assumes that this growth is only due to the instruction for reading comprehension. There seems to be quite a bit of contribution of skills gained due to the first two years of mathematics instruction to subsequent performances in reading comprehension.

Figure 4(a) shows that on the one hand , pupils with a plus one standard deviation difference (+1SD) in prior mathematics (Math2_1) achievement (ReadBTMGCM+1SD) tend to have a lower end of grade 3 reading comprehension score but a steeper growth subsequently. On the other hand it indicates that, pupils with minus one standard deviation difference (ReadBTMGCM-1SD), show a less steep growth in reading comprehension. Not surprising though, pupils with a +1SD difference (MathBTMGCM+1SD) in prior mathematics achievement showed a steeper growth than pupils with a -1SD difference (MathBTMGCM-1SD) from the end of grade3 to the end of grade 6.

Figure 4 BTMGCM profiles for pupils with +1SD and -1SD of difference in prior mathematics achievement a) Reading comprehension and b) Mathematics.

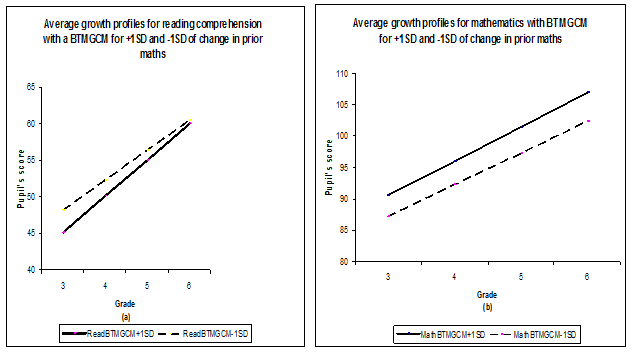
After considering the BTMGCM with earlier and later prior change in mathematics achievement as covariates, the results of variance-covariance parameters of the BMGCM are then compared with those of the BTMGCM and presented in Table 4.

Variance parameter	BMGCM			BTMGCM (I)
Variance parameter	Estimate	Std error	Correlation	Estimate	Std error	Correlation
Math status	67.629	1.435	1	62.776	1.52	1
Math slope	0.594	0.087	1	0.599	0.094	1
Read status	47.184	1.038	1	46.355	1.165	1
Read slope	0.888	0.083	1	0.882	0.091	1
Covariance parameter
Math status – Math slope	-1.408	0.293	-0.222	-1.884	0.318	-0.307
Read status – Read slope	-0.555	0.243	-0.086	-0.552	0.268	-0.086
Math status - Read status	39.025	1.011	0.691	37.922	1.107	0.703
Math status - Read slope	1.255	0.279	0.162	0.984	0.307	0.132
Math slope - Read status	-0.501	0.263	-0.095	-0.667	0.254	-0.127
Math slope - Read slope	0.284	0.062	0.391	0.245	0.067	0.337

a) Student level variance parameters
Math=mathematics, Read=reading comprehension, status is the student intercept at the end of grade 3 and slope= linear growth.

Variance parameter	BMGCM			BTMGCM (I)
Variance parameter	Estimate	Std error	Correlation	Estimate	Std error	Correlation
Math status	15.44	1.917	1	13.746	1.839	1
Math slope	1.079	0.137	1	1.177	0.158	1
Read status	12.373	1.508	1	9.391	1.3	1
Read slope	0.676	0.093	1	0.676	0.099	1
Covariance parameter
Math status – Math slope	-1.231	0.383	-0.302	-1.606	0.408	-0.399
Read status – Read slope	-0.712	0.274	-0.246	-0.766	0.266	-0.304
Math status - Read status	9.277	1.439	0.671	8.023	1.325	0.706
Math status - Read slope	-0.05	0.299	-0.015	-0.303	0.301	-0.099
Math slope - Read status	-0.474	0.325	-0.13	-0.893	0.329	-0.268
Math slope - Read slope	0.497	0.09	0.582	0.579	0.102	0.649

b) School level variance parameters
Estimates in bold are not significant at a 5% level. Math=mathematics, Read=reading comprehension, status is the student intercept at the end of grade 3 and slope= linear growth.

Table 4 Estimates of variance and covariance components for the bivariate multilevel growth curve model (BMGCM) compared with the bivariate transition multilevel growth curve model (BTMGCM (I))

The results are quite similar in terms of the direction of the covariance though the BMGCM seem to yield higher estimates for most of the parameters as compared to the BTMGCM (I). However, one conspicuous difference is the significant correlation (-0.268) between the average school intercept in reading comprehension and average slope in mathematics for the BTMGCM, which is not significant in the BMGCM. This means schools with a higher average score in reading comprehension at the end of grade 3 do not grow as fast in mathematics in comparison to schools with a lower average score. In other words, the higher the school’s average reading comprehension score at the end of grade 3, the lower the growth of the school in mathematics from the end of grade 3 to the end of grade 6.

The school effect estimates for mathematics and reading comprehension on the pupils’ status and growth were obtained for the different growth models described previously in this paper. The school effects are estimated as the proportion of variance accounted by the school level compared to that at the pupil level.²⁵ The results of the school effect estimates under the three different models are summarised in Table 5 below. The results indicate that univariate growth curve models seem to overestimate the effect of schools on the pupils at the end of grade 3 for both reading comprehension (27.5%) and mathematics (23.6%). The improved BMGCM estimates the same effects as 22.8% for reading comprehension and 18.6% for mathematics. However, the UMGCM seem to underestimate the school effect on growth with estimates of 34.6% and 47.6% for reading comprehension and mathematics respectively. Looking at the same estimates using the BMGCM, they increase to 43.2% and 64.5% for reading comprehension and mathematics respectively. This means that assuming a joint bivariate growth in the pupils reading comprehension and mathematics achievement can result in larger estimates of the effects of schools on the pupils’ growth than treating the outcomes as if they were independent of each other.

At the end of Grade 3
Reading comprehension
School effect on student status	27.5%	22.8%	16.8%
School effect on student linear growth	34.6%	43.2%	43.4%
Mathematics achievement
School effect on student status	23.6%	18.6%	18.0%
School effect on student linear growth	47.6%	64.5%	66.5%

Table 5 The school effect estimates for the pupils’ status and growth in reading comprehension and mathematics at the end of grade 3, for the three growth curve models described

The BTMGCM is fitted to remove the false assumption that the bivariate growth process started at the end of grade 3 for both pupil outcomes ignoring the first three measurements of mathematics. It is possible that knowledge acquired during the first two grades of primary school, might be responsible not only in the better fit of the model as shown earlier but also help avoid the fallacy of missing at random assumption for this data structure. With the BTMGCM, changes were observed in the school effect estimates on the pupils’ status in reading comprehension (16.8%) and the growth in mathematics (66.5%).

This Table 5 also indicates that schools have a larger effect on their pupils’ mathematics growth than on their growth in reading comprehension.

Discussion

Considering the correlation results, the UMGCM shows no significant relationship between the pupils’ status and growth in reading comprehension. The UMGCM also underestimates the effect of schools on pupils’ linear change in mathematics as well as reading comprehension. However, this effect became significant in the BMGCM indicating better power in the latter model. The BMGCM results also illustrate that pupils’ who are higher achievers in mathematics at the end of grade 3 are also higher achievers in reading comprehension at the end of grade 3. Pupils with a stronger growth in mathematics also show a stronger growth in reading comprehension. Pupils who score high in mathematics at the end of grade 3 grow more in reading comprehension subsequently. However, pupils who are higher achievers in reading comprehension at the end of grade 3 experience a slower growth in mathematics.

At the school level, the correlation between the average reading comprehension at the end of grade 3 and the average mathematics at the end of grade 3 was significant. This implies schools with high achieving pupils in mathematics also have high achievers in reading comprehension. Also schools with a high average growth in reading comprehension have a high average growth in mathematics.

The significant correlation between the overall mathematics achievement and reading comprehension growth profiles is an indication that statistically a BMGCM approach is more appropriate. The BMGCM also resulted in about 35% increase in the school effect estimate on pupils’ growth in mathematics and about 25% increase for pupils’ growth in reading comprehension. However, the school effect on the pupils’ status dropped by 21% and 17% for mathematics and reading comprehension respectively. The univariate model seems to overestimate the differences between schools by the end of grade 3. The UMGCM also underestimates the effect of schools on pupils’ linear change in mathematics as well as reading comprehension. This is far enough evidence of the need for more than one criterion to better estimate the effects of schools on primary school children. The results of the BMGCM also show more clearly that the effect of schools is more pronounced on the pupils’ growth criterion than on the status. The school effects on the pupils’ growth is about 3.7 times larger than on the pupils’ status at the end of grade 3 for mathematics achievement and about 2.6 times more for reading comprehension. The same comparison at the beginning of grade 3 indicates that the school effect on pupils’ growth is about 1.9 times for mathematics and about 1.5 times for reading comprehension. Analysis at the end of grade 6 (not presented) corroborates these findings and also results of previous studies on longitudinal data.^22,33 It is nonetheless advisable to fit models with many more first stage criteria than just two as in this study (mathematics and reading comprehension), in order to generalise these findings. This can be considered a relative advantage of the choice of the growth criterion over the status criterion at the second stage for both first stage criteria because schools seem to have more impact on it.

The results of the transition model showed that changes in mathematics achievement in the first and second grade could predict the change in reading comprehension in the later grades. When prior growth in mathematics is taken into account, the schools seem to help the low achievers at the end of grade 3 to catch up with their higher achieving peers by the end of grade 6. In other words pupils with a larger gain in earlier mathematics achievement grow faster in reading comprehension subsequently though they are low achievers at the end of grade 3.

The BMGCM showed no significant correlation between the schools’ average mathematics score at the end of grade 3 and the growth in reading comprehension. A similar non-significant result is obtained for the correlation between the school’s average score in reading comprehension at the end of grade 3 and the growth in mathematics. However, with the introduction of the BTMGCM, the correlation between the schools’ average score in reading comprehension and the schools average growth in mathematics became significant. The school level correlations indicate that schools that are effective in the pupils’ average mathematics achievement are also effective in their average reading comprehension attainment on both the status and growth criteria.

From the findings of this study, we recommend that researchers in the field of school effectiveness should consider multiple criteria to enable this field of research come up with improved school effect estimates. We encourage researchers to make more use of longitudinal data and the two-stage criteria proposed, to enable researchers to answer a wider range of scientifically relevant questions to school effectiveness research. We acknowledge the computational difficulties that such complex models with multiple stage 1 and 2 criteria will bring while recognising the invaluable contribution it will make to the field of educational effectiveness. The multivariate transition model proposed in this paper can be used by researchers to avoid false missing assumptions or even the loss of data and in addition can answer other very relevant research questions.

We were not able in our study to investigate the more appropriate joint causal change relationship. It would have been interesting for example to investigate whether the change in mathematics influences the change in reading comprehension and not the other way around. Nevertheless, this study serves as a strong foundation on which more complex educational research methods can be developed.^34–41