In global healthcare data analysis such as the consequences due to volcanic eruptions, the threee main random variables (ash in proportion, spilled distance in kilo meter, and angle direction of the wind) are seemingly independent but their data indicate correlations otherwise. This apparent conflict requires a careful scruitiny and selection of appropriate underlying model for the data in more realistic sense rather than the analyst’s convenience. For this purpose, a trivariate probability density function (PDF), with a bonding function of the variables and a flexing parameter, is introduced and investigated with its statistical properties in this article. The flexing parameter allows the PDF to explain the so called sampling bias in the collected data. The locations which received more debris have higher chance of being included in the data collection and it is what the statistics literature calls “sampling bias.” The flexing parameter enriches the versatility of the model. Such a novelty based new PDF is named flexing and bonding trivariate distribution (FBTD) in this article. Several expressions for FBTD are derived and illustrated using data about the eruption of Eyjafjallajokull volcano, Iceland on 14th April 2010 as it disrupted flights, voyages, travels, and life itself not only in Europe but also elsewhere.

Keywords: probability, model, parameters, correlation, data analysis, ,maximum likelihood

Millions of people suffer due to volcanic gases worldwide. Health hazards in volcanic gases¹ like SO₂ H₂S and CO₂ cause fatalities from asphyxiation.² Chronic exposure to H₂S increases respiratory diseases.^3,4 Natural hazards like the 14^th April 2010 eruption of Eyjafjallajokull volcano, Iceland cause global public health hazards within a radius of distance from its epi-center in several directions of measurable angle due to wind.^5,6 The metallic and heavy substances in the ash are trigger illness.⁴ Learning from such natural calamity data may not help to prevent it but surely assists to reduce health damages.⁷ Developing an appropriate model for the data is a starting point. Modeling such trivariate volcanic data has been a challenge to those who wish to analyze and interpret data evidence.⁸ A reason is that the variables are seemingly independent but are correlated otherwise, according to the data (Table 1, Figures 1 and 2). This is a conflict. Such a conflict is not unique to volcanic data analysis but also in tsunami, cyclone, earthquake, and cancer data analysis. In an analogues manner, the breast cancer research comes across a similar scenario. The malignant cells spread in an area of distance at some direction with a varying carcinogenic intensity level. An appropriate model for the collected data of a specific scenario is a necessity to interpret the data evidence. What is model? Model is an abstraction of reality. To echo the reality, the model ought to have appropriate ingredients. How should a data analyst create a model which integrates seemingly independent but rather correlated random variables with a meaningful versatility and interpretability is the aim of this article. To attain this aim, this article innovatively introduces a non-negative bonding function $w(\varphi )$  with a flexing parameter $\varphi >0$ . When the flexing parameter $\varphi =0$ , the model exhibits the trivial scenario of mutual independence of the data variables as special cases. In modeling volcanic debris data, the affected distance ( ) and the direction angle ( ) of the wind are seemingly independent random variables. Assume their probability density functions (PDF) are

$f(d|\alpha ,\beta )={\beta }^{\alpha }{d}^{\alpha -1}{e}^{-d/\beta }/\Gamma (\alpha );d>0$ ,
with shape and rate parameters $\alpha >0$ and $\beta >0$ $f(\theta )=1/2\pi ;\theta >0$ .

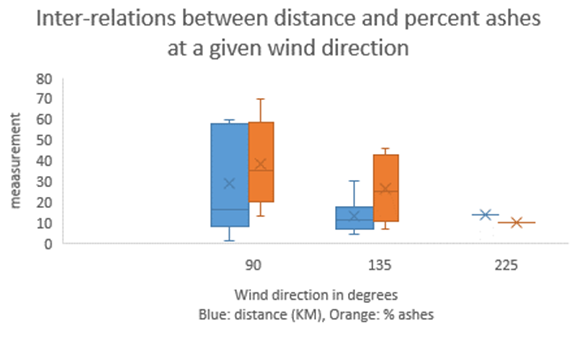
Figure 1 Box plots of distance and percent ashes at a given wind direction.

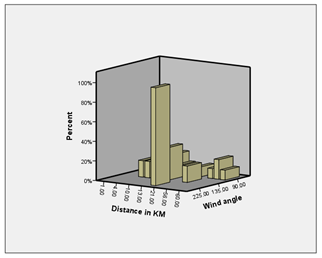
Figure 2 The 3-dimensional inter-relations of $y,d,\theta$ .

The third variable is percent, $Y$ ash mass and it is assumed to follow independently a beta distribution,

$f(y|\delta ,\gamma )=\Gamma (\delta +\gamma )y^{\delta -1}{(1-y)}^{\gamma -1}/\Gamma (\delta )\Gamma (\gamma );0<y<1;$

with parameters $\delta ,\gamma >0$ .

The variance of the distance is $Var(d|\alpha ,\beta )=\beta E(d|\alpha ,\beta )$ , where the expected distance is $E(d|\alpha ,\beta )=\alpha \beta$ . The parameter $\beta$ captures the proportionality of the expected amount in variance. Furthermore, the entropy “ $-E\ln f(d|\alpha ,\beta )$ ” of the distance is minimally “ $\ln \beta$ ” but it increases at a rate $\alpha +\ln \Gamma (\alpha )+(1-\alpha )\psi (\alpha )$ , where $\psi (\alpha )$ is the well-known digamma function.The parameter $\alpha$ portrays the increment.

The variance of the distance is $Var(d|\alpha ,\beta )=\beta E(d|\alpha ,\beta )$ , where the expected distance is $E(d|\alpha ,\beta )=\alpha \beta$ . The parameter $\beta$ captures the proportionality of the expected amount in variance. Furthermore, the entropy “ $-E\ln f(d|\alpha ,\beta )$ ” of the distance is minimally “ $\ln \beta$ ” but it increases at a rate $\alpha +\ln \Gamma (\alpha )+(1-\alpha )\psi (\alpha )$ , where $\psi (\alpha )$ is the well-known digamma function.The parameter $\alpha$ portrays the increment.

The variance of the angle is $Var(\theta )=\frac{{\{E(\theta )\}}^2}{3}$ , where the expected angle of the wind direction is $E(\theta )=\pi$ . The entropy “ $-E\ln f(\theta )$ ” of the angle is “ $\ln (2\pi )$ ”.

The variance of the percent ash is

$Var(y|\delta ,\gamma )=E(y|\delta ,\gamma )\{1-E(y|\delta ,\gamma )\}/(\delta +\gamma +1)$ ,

where the expected ash is $E(y|\delta ,\gamma )=\frac{\delta }{(\delta +\gamma )}$ .

The entropy “ $-E\ln f(y|\delta ,\gamma )$ ” of the percent ash spread is

$\ln \Gamma (\delta +\gamma )-\ln \Gamma (\delta )-\ln \Gamma (\gamma )-(\delta -1)\psi (\delta )-(\gamma -1)\psi (\gamma )+(\delta +\gamma -2)\psi (\delta +\gamma )$ .

In other words, $f(y,\theta ,d)=p(y)q(\theta )r(d)$ , where $p(y)$ , $q(\theta )$ and $r(d)$ denote respectively marginal PDF of the data variables y, $d$ and $\theta$ . Shanmugam and Chattamvelli⁹ for derivations and statistical details about beta, gamma and uniform distributions.

On the contrary to a seeming impression that the three random variables y, $d$ and $\theta$ are independent, their data (Table 2) exhibit correlated, simply negating the assumption of their independence. Such a data based clue warrants a necessity to derive a realistic trivariate PDF for the collected data. This necessity results in an innovative and realistic model with a bonding function $w(\varphi ,y,\theta ,d)$ in which $\varphi >0$ is recognized as a flexing parameter for the sake of versatility as it is done in this article.

This trivariate PDF (1) is new to the literature and hence, it is named flexing and bonding trivariate distribution (FBTD). The statistical properties of FBTD are done first in Section 2 and are illustrated later in Section 3. Final comments are made in Section 4.¹⁰

To be realistic, the data collection process is sometimes tilted unevenly in the collection of natural calamities such volcanic eruptions. The tilted sampling process is recognized as length-biased sampling with a weight factor $w(d,\theta )$  in statistics literature. Then, what is an appropriate weight factor in our scenario? A rationality for selecting the weight factor is the following. The area in which the volcanic debris is found is proportional to the circular circumference $2\pi d$ with radius distance $d>0$ . Such proportionality is well connected to an angle, $\theta >0$ due to wind direction and hence, it is $\frac{\theta }{2\pi }(2\pi d)=\theta d$ .

In addition to this proportionality in the weight factor, a flexibility to condense or expand the proportionality is needed and it is done by introducing a finite and non-negative flexible parameter $\varphi >0$  so that the weight function becomes $w(\varphi ,d,\theta )\propto (1+\varphi \theta d)$ to accompany the PDF $f(d,\theta )$ . Because of the third variable Y, the sampling bias weight function is expanded to $w(y,\theta ,d)=(1+\varphi y\theta d)$ . In other words, the trivariate PDF of the percent ashes, radius distance, and angle of wind in the collected data is

$\begin{array}{l}f(y,\theta ,d,\varphi )=\frac{(\Gamma [\delta +\gamma +1])(1+\varphi y\theta d)d^{\alpha -1}{e}^{-d/\beta }{y}^{\delta -1}{(1-y)}^{\gamma -1}}{{\beta }^{\alpha }2\pi (\gamma +[1+\varphi \pi \alpha \beta ]\delta )\Gamma (\delta )\Gamma (\gamma )\Gamma (\alpha )};\\ 0<y<1;0<\theta <2\pi ;d,\delta ,\gamma ,\varphi ,\alpha ,\beta ,>0\end{array}$ (1)

It is straightforward to check out that $f(y,\theta ,d,\varphi )$ in (1) is a bona fide PDF, since $f(y,\theta ,d,\varphi )\ge 0$ and

${\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}f(y,\theta ,d,\varphi )\partial \theta \partial d\partial y}}}=1$ .

With no flexibility (that is, $\varphi =0$ ), the FBTD (1) precipitates to a product of the three (that is, gamma, circular uniform, and beta) bona fide marginal PDFs, implying that the three data variables (percent volcanic ash Y, $D$ affected distance and wind direction angle $\theta$ ) are all stochastically mutually independent (as, $f(y,\theta ,d)=f(y)f(\theta )f(d)$ ). Otherwise (that is, when $\varphi \ne 0$ ), the data variables are all mutually and stochastically dependent (that is, $f(y,\theta ,d,\varphi \ne 0)\ne f(y)f(\theta )f(d)$ ). The flexing parameter $\varphi$ helps to construct a contour mapping of similarly affected places by volcanic debris. The product moment of the FBTD (1) is

$\begin{array}{l}E(y^m{d}^n{\theta }^p)={\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{y}^m{d}^n{\theta }^{p}f(y,\theta ,d,\varphi )\partial \theta \partial d\partial y}}}\\ ={\displaystyle \underset{0}{\overset{1}{\int }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{y}^m{d}^n{\theta }^p\frac{(\Gamma [\delta +\gamma +1])(1+\varphi y\theta d)d^{\alpha -1}{e}^{-d/\beta }{y}^{\delta -1}{(1-y)}^{\gamma -1}}{2\pi {\beta }^{\alpha }(\gamma +[1+\varphi \pi \alpha \beta ]\delta )\Gamma (\delta )\Gamma (\gamma )\Gamma (\alpha )}\partial \theta \partial d\partial y}}}\\ =\frac{{(2\pi )}^p{\beta }^n}{(\gamma +[1+\varphi \pi \alpha \beta ]\delta )}\frac{\Gamma (n+\alpha )}{\Gamma (\alpha )}\frac{\Gamma (m+\delta )}{\Gamma (\delta )}\frac{\Gamma (1+\delta +\gamma )}{\Gamma (m+\delta +\gamma )}\{\frac{1}{(p+1)}+\frac{2\pi \varphi \beta (n+\alpha )(m+\delta )}{(p+2)(m+\delta +\gamma )}\}\end{array}$ (2)

Note that, with $m=0=n=p$ , the expression (2) is one as it should be. With $m=1=n=p$ , the trivariate product moment, $E(yd\theta )$ is obtained and it is

$E(yd\theta )=E(y)E(d)E(\theta )\left\{\frac{1+\frac{4\varphi E(\theta )[\beta +E(d)](1+\delta )}{3(1+\delta +\gamma )}}{1+\varphi E(y)E(d)E(\theta )}\right\}$ . (3)

In the absence of flexibility or equivalently referring independence among the three random variables (that is, $\varphi =0$ ), the product moment (3) breaks up to a product $E(y)E(d)E(\theta )$ of their marginal moments. The expected amount, $E(yd\theta )$ in (3) is at its base $E(y)E(d)E(\theta )$ when $\varphi =0$

and later increases at a rate $\left\{\frac{1+\frac{4\varphi E(\theta )[\beta +E(d)](1+\delta )}{3(1+\delta +\gamma )}}{1+\varphi E(y)E(d)E(\theta )}\right\}$ ,

when $\varphi \ne 0$ . We define, in this article, the trivariate product variance $Var(yd\theta )$ as $Var(yd\theta )=E(y^2{d}^2{\theta }^2)-{\{E(yd\theta )\}}^2$ . Using (2) and (3), we obtain that

$\begin{array}{l}Var\left(yd\theta \right)\approx \frac{4{\pi }^2{\beta }^2\alpha \delta }{(\gamma +[1+\varphi \pi \alpha \beta \left]\delta \right)}\left\{\frac{(1+\alpha )(1+\delta )}{(1+\gamma +\delta )}\right[\frac{1}{3}+\frac{\varphi \pi \beta (2+\alpha )(2+\delta )}{2(2+\gamma +\delta )}]\\ -\frac{\alpha \delta }{(\gamma +[1+\varphi \pi \alpha \beta \left]\delta \right)}[\frac{1}{2}+\frac{2\varphi \pi \beta (\alpha +1)(\delta +1)}{3(1+\gamma +\delta )}{]}^2\}\end{array}$ (4.a)

The variance $Var(yd\theta )$ in (4.a) is at its base

$Var(yd\theta )\approx \frac{4{\pi }^2{\beta }^2\alpha \delta }{(\gamma +\delta )}\{\frac{(1+\alpha )(1+\delta )}{3(1+\gamma +\delta )}-\frac{\alpha \delta }{4(\gamma +1)\delta }\}$ (4.b)

when $\varphi =0$ and it later changes when $\varphi \ne 0$ . The predictability becomes less precise when the variance is more and vice versa.

Of interest to healthcare researchers is of course the ability to predict one among the three data variables: $y,d,\theta$  based on patterns in the other two variables. This requires configuring their conditional PDFs. Suppose a healthcare researcher at a known distance from the epi-center of a volcanic with an observable wind direction $\Theta =\theta$ wonders about receiving an average amount of ash. For this purpose, the conditional PDF, $f(y|\theta ,d)$ is needed. That is,

$\begin{array}{l}f\left(y|\theta ,d\right)=\frac{f(y,\theta ,d)}{f(\theta ,d)}=\frac{\Gamma (\gamma +\delta +1)(1+\varphi y\theta d)}{\Gamma \left(\gamma \right)\Gamma \left(\delta \right)(\gamma +[1+\varphi \theta d\left]\delta \right)}{y}^{\delta -1} (1-y{)}^{\gamma -1};\\ 0<y<1,\gamma ,\delta ,\theta ,d>0\end{array}$

The expected ash amount, $E(y|\theta ,d)$ starts a base value $E(y)=\frac{\delta }{(\gamma +\delta )}$ and increases at a

$rate=\frac{E(y|\theta ,d)}{E(y)}=\frac{(1+\frac{\varphi \theta d[\delta +1][\gamma +\delta ]}{[\gamma +\delta +1]})}{(1+\frac{\varphi \theta d\delta }{[\gamma +\delta ]})}$

depending on the wind direction and distance. The rate is greater than one, meaning that $E(y|\theta ,d)>E(y)$ . What does it imply? The conditional average predictive percent, $E(y|\theta ,d)$ of the ashes based on known wind direction angle, $\theta$ and the distance, $d$ is more than the unconditional average predictive percent, $E(y)$ of ashes without knowing wind direction and location distance. Likewise, we notice that $Var(y|\theta ,d)\le Var(y)$ . The implication is that the conditional average predictive percent of the ashes based on known wind direction angle, $\theta$ and the distance, $d$ is more precise (because lesser variance means more precise) than the unconditional average predictive percent of the ashes without knowing the wind direction and location distance.

Agencies responsible to protect the public healthcare often want to project the expected distance, $E(d|\theta ,y)$ based on knowing the angle, $\theta$ of the wind direction and the percent $y$ of spreading ashes. This requires configuring the conditional PDF, $f(d|\theta ,y)$ of the distance $D=d$ from the epi-center of a volcanic with an observable wind direction $\Theta =\theta$ and measurable percent of the volcanic ash, $Y=y$ and it is,

  $\begin{array}{l}f(d|\theta ,y)=\frac{f(y,\theta ,d)}{f(\theta ,y)}=\frac{(1+\varphi y\theta d)}{{\beta }^{\alpha }(1+\varphi y\alpha \beta \theta )\Gamma (\alpha )}{e}^{-\frac{d}{\beta }}{d}^{\alpha -1};\\ 0<d<1;y,\theta ,\alpha ,\beta >0\end{array}$

The expected distance, $E(d|\theta ,y)$ starts at a baseline $E(y)=\alpha \beta$ and it increases at a

$rate=\frac{E(d|\theta ,y)}{E(d)}=\frac{(1+\varphi y\beta \theta [\alpha +1])}{(1+\varphi y\beta \theta \alpha )}$

which is greater than one. It means that $E(d|\theta ,y)>E(d)$ . What does it imply? The conditional average predicted distance, $E(d|\theta ,y)$ for the ashes based on the known wind direction angle, $\theta$ and the perceived percent, $y$ of ashes is more than the unconditional average predictive distance, $E(d)$ of the ashes without knowing wind direction and the percent of ashes spreading. Likewise, we notice that

$Var(d|\theta ,y)=Var(d)[\frac{1+\varphi y\alpha \beta \theta \{1+(\alpha +1)(\alpha +1+\varphi y\beta \theta )\}}{{(1+\varphi y\alpha \beta \theta )}^2}]$

Implying $Var(y|\theta ,d)\ge Var(y)$ . The conditional average projected distance to receive ashes based on known wind direction angle, $\theta$ and the percent of spreading ashes, $y$ is less precise (because more variance means lesser precision) than the unconditional average projected distance to receive ashes without knowing wind direction angle, $\theta$ and the percent of spreading ashes, $y$ .

Proceeding likewise, having already observed a percent, y of the volcanic ashes at a known distance, d from the epi-center of the volcano, an environmental researcher could have done an educated guess of the angle of wind direction on the eruption day. For this purpose, the conditional PDF, $f(\theta |y,d)$ of the angle is needed and it is

$\begin{array}{l}f(\theta |y,d)=\frac{f(y,\theta ,d)}{f(y,d)}=\frac{(1+\varphi y\theta d)}{2\pi (1+\varphi yd\pi )};\\ 0<\theta <2\pi ;y,d,\pi >0\end{array}$

The educated guess, $E(\theta |y,d)$ of the angle of the wind direction starts at a baseline $E(y)=\pi$ with an $adjustment=\frac{E(\theta |y,d)}{E(\theta )}=\frac{(1+\frac{4\varphi yd\pi }{3})}{(1+\varphi yd\pi )}$ which is greater than one, meaning that $E(\theta |y,d)>E(\theta )$ . What does it imply? The educated conditional average guess, $E(\theta |y,d)$ of the angle based on known percent ashes, $y$ at location distance, $d$ is more than the unconditional average guess angle, $E(\theta )$ of wind direction without knowing percent of ashes at a location distance, $d$ . Furthermore, we notice that

  $Var(\theta |y,d)\approx Var(\theta )\left\{\frac{1+2\varphi yd\pi (1+\frac{\varphi yd\pi }{3})}{{(1+\varphi yd\pi )}^2}\right\}$

implying $Var(\theta |y,d)\le Var(\theta )$ . The educated average guess of the angle for wind direction based on known percent, $y$ of ashes at distance, $d$ is more precise than the uneducated average guess of wind direction without knowing percent ashes at location of distance d.

We now proceed to estimate the model parameters from a collected data. Consider a random sample $y_i,{\theta }_i,d_i$ of size $n\ge 2$ from FDTD (1). Let $\overline{y},\overline{\theta },\overline{d}$ and $s_y^2,s_{\theta }^2,s_d^2$ denote respectively their sample average and variance. The log-likelihood function is $L(n,y,\theta ,d,\varphi )={\displaystyle \sum _{i=1}^n\ln f(y_i,{\theta }_i,d_i,\varphi )}$ . Then, their maximum likelihood estimators (MLE) are the simultaneous solutions of the score functions ${\partial }_{\varphi }L(n,y,\theta ,d,\varphi )=0$ , ${\partial }_{\alpha }L(n,y,\theta ,d,\varphi )=0$ , ${\partial }_{\beta }L(n,y,\theta ,d,\varphi )=0$ , ${\partial }_{\delta }L(n,y,\theta ,d,\varphi )=0$

${\partial }_{\gamma }L(n,y,\theta ,d,\varphi )=0$ and ${\partial }_{\pi }L(n,y,\theta ,d,\varphi )=0$ . They yield

${\widehat{\varphi }}_{mle}\approx \left|\frac{{\displaystyle \sum _{i=1}^n{y}_i{\theta }_i{d}_i-n{\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o}}{{\displaystyle \sum _{i=1}^n{(y_i{\theta }_i{d}_i)}^2-n{({\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o)}^2}}\right|$ (5.a)

${\widehat{\pi }}_{mle}=\left|{\widehat{\pi }}_o-\frac{\widehat{\varphi }\overline{d}{\widehat{\delta }}_o}{({\widehat{\gamma }}_0+{\widehat{\delta }}_o)}\right|$ , (5.b)

${\widehat{\alpha }}_{mle}=\left|{\widehat{\alpha }}_o-\frac{\widehat{\varphi }{\widehat{\beta }}_o{\widehat{\delta }}_o}{({\widehat{\gamma }}_0+{\widehat{\delta }}_o)}\right|$ , (5.c)

${\widehat{\beta }}_{mle}=\left|{\widehat{\beta }}_o-\frac{\widehat{\varphi }{\widehat{\delta }}_o}{({\widehat{\gamma }}_0+{\widehat{\delta }}_o)}\right|$ , (5.d)

${\widehat{\delta }}_{mle}=\left|{\widehat{\delta }}_o-\frac{\widehat{\varphi }}{({\widehat{\gamma }}_0+{\widehat{\delta }}_o)}\right|$ , (5.e)

and

${\widehat{\gamma }}_{mle}=\left|{\widehat{\gamma }}_o-\frac{\widehat{\varphi }{\widehat{\delta }}_o}{({\widehat{\gamma }}_0+{\widehat{\delta }}_o)}\right|$ , (5.f)

where the initial values ${\widehat{\pi }}_o={\theta }_{(n)}=\max ({\theta }_1,{\theta }_2,\mathrm{...},{\theta }_n)$ , ${\widehat{\alpha }}_o=\frac{s_d^2}{\overline{d}}$ , ${\widehat{\beta }}_o=\frac{\overline{d}}{\widehat{\alpha }}$ , ${\widehat{\delta }}_o=\frac{\overline{y}(1-\overline{y})}{s_y^2}-1$ , ${\widehat{\gamma }}_o=(1-\overline{y})\widehat{\delta }$ are obtained from the sample averages and variances. In the next section, all derived expressions of this section are illustrated.

From (5.a), we note that the product variables to be considered are

$\left\{\frac{y_1{\theta }_1{d}_1-{\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o}{{(y_1{\theta }_1{d}_1)}^2-{({\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o)}^2}\right\}$ $\left\{\frac{y_2{\theta }_2{d}_2-{\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o}{{(y_2{\theta }_2{d}_2)}^2-{({\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o)}^2}\right\}$ ,…., $\left\{\frac{y_n{\theta }_n{d}_n-{\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o}{{(y_n{\theta }_n{d}_n)}^2-{({\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o)}^2}\right\}$ .

With the MLE ${\widehat{\varphi }}_{mle}$ of the flexible parameter and expressions (3) and (4.b), an approximate $100(1-\alpha )\%$ confidence interval for $0<\alpha <1$ can be constructed and it is

$\varphi \in {\widehat{\varphi }}_{mle}\pm \frac{t_{(n-1)df,1-\frac{\alpha }{2}}{s}_{\left\{\frac{y\theta d-{\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o}{{(y\theta d)}^2-{({\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o)}^2}\right\}}}{\sqrt{n}}$ (6)

where

$\begin{array}{l}{s}_{\left\{\frac{y\theta d-{\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o}{{(y\theta d)}^2-{({\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o)}^2}\right\}}=\sqrt{\frac{{\displaystyle \sum _{i=1}^n{{(}_{\left\{\frac{y\theta d-{\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o}{{(y\theta d)}^2-{({\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o)}^2}\right\}}-\left\{\frac{{\displaystyle \sum _{i=1}^n{}_{\left\{\frac{y\theta d-{\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o}{{(y\theta d)}^2-{({\widehat{\pi }}_o{\widehat{\alpha }}_o{\widehat{\beta }}_o{\widehat{\delta }}_o)}^2}\right\}}}}{n}\right\})}^2}}{(n-1)}}\\ \end{array}$

is the standard error of the product variables.

The 39-day long eruption of Eyjafjallajokull volcano, Iceland started on 14^th April 2010 and continued on to 13^th May 2010. The ash was seen as far as 100 Kilo Meters in several directions from 900 to 2250 due to the wind. The percent of ashes varied up to 63 $\mu m$ (Table 1). Several jet-engine powered aircrafts were strained, not able to fly as they were exposed to volcanic ash. Due to the prevailing winds, the ash spread out mostly to the southeast, and south, closing the entire European air space for several days. The health hazards were rising among the residents in Europe and even beyond. Exposure to the volcanic ash had adverse effects on respiratory health. The short-term effects of the ash exposure were irritation in eyes, upper airway, or asthma type discomforts. Table 1 for observations on the wind’s angle, the distance up to which the debris is spread out, and the percent of ashes on the sampled days. Their averages and variances are calculated and displayed in Table 1. They warn the existence of their unpredictability. The Table 2 points out their non-zerocorrelations, emphasizing the importance of bonding and flexing the three random variables. Especially, the correlation (0.77) between the distance in kilo meter and the percent of ashes is significant at a p-value 0.0001, emphasizing the importance bonding and flexing the data variables.

The initial parametric values, according to the displayed data averages and variances in Table 1, are obtained. They are ${\widehat{\pi }}_o={\theta }_{(n)}={225}^o$ , ${\widehat{\alpha }}_o=11.38$ , ${\widehat{\beta }}_o=1.96$ , ${\widehat{\delta }}_o=4.36$ , ${\widehat{\gamma }}_o=2.95$ . From (5.a), we obtain that ${\widehat{\varphi }}_{mle}\approx 1.57$ which is much higher than zero. It is no wonder the three data variables are not independent. The MLE of the model parameters, from (5.b) through (5.f) are ${\widehat{\pi }}_{mle}={194.7}^o$ , ${\widehat{\alpha }}_o=9.54$ , ${\widehat{\beta }}_o=1.02$ , ${\widehat{\delta }}_o=4.14$ , ${\widehat{\gamma }}_o=2.01$ . Using the expression (6), an approximate 95% confidence interval is computed and it is $\varphi \in (1.57\pm 0.000002)$ . A measure of goodness-of fit may be based on the log-likelihood statistic. Then one may test the hypothesis H₀: $\varphi =0$  against H₁: $\varphi \ne 0$  by using the likelihood ratio test.

In some instances but not always, the percent of ashes might proportionally decrease as the distance increases only if the wind is stable. Otherwise, the percent of ashes might be more in a faraway distance if the wind is blowing at an angle and strongly. A realistic probability model is identified and applied to volcanic data analysis. In the model, a parametric symptom is introduced and utilized in this article to check out whether or not the wind direction, distance for volcanic debris, and the percent of ashes have functioned as disconnected entities in a particular natural disaster. With a new and novel flexing and bonding trivariate probability density function (1), we have proved that the three data variables (namely, ash in proportion, spilled distance in kilo meter, and angle direction of the wind) are not independent because ${\widehat{\varphi }}_{mle}\approx 1.57$ which is much higher than zero. Recall that $\varphi =0$ is a requirement for the three data variables to be independent.

The authors appreciates and thanks an anonymous referee for valuable suggestions which helped to improve contents and quality of the article.

None

1. Beaubien SE, Ciotoli G, Lucchese R. Carbon dioxide and radon gas hazard in the Alban Hills area (central Italy). J Volcanol Geotherm Res. 2003;123:63‒80.
2. Simkin T, Siebert L, Blong R. Volcano Fatalities‒Lessons from the historical record. Science. 2001;291(5502):255.
3. Annuziatellis A, Ciotoli GLombardi S. Short‒ and long‒term gas hazard: the release of toxic gases in the Alban Hills volcanic area (central Italy). J Geochem Exploration. 2003;77:93‒108.
4. Small D, Naumann The global distribution of human population and recent volcanism. Environ Haz. 2001;3:93‒109.
5. Gıslason SR, Alfredsson HA, Eiriksdottir ES, et al. Volcanic ash from the 2010 Eyjafjallajokull eruption. Applied Geochemistry. 2011;26:S188‒S190.
6. Grattan J, Durand M, Gilbertson D. Human sickness and mortality rates in relation to the distant eruption of volcanic gases: rural England and the 1783 eruption of the Laki fissure, Iceland. In: Geology and Health: Closing the Gap, Skinner HCW & Berger A (Ed.) Oxford: Oxford University Press, USA. 2003;p. 19‒24.
7. World Health Organization (2010) Volcanic Ash Cloud over Europe.
8. Durand M, Grattan J. Effects of volcanic air pollution on health. Lancet. 2001;357:164. 
9. Shanmugam R, Chattamvelli R. Statistics for Scientists and Engineers, John Wiley Press, 111 River Street, Hoboken, NJ. 2015;07030‒5774, ISBN: 978‒1‒118‒228968.
10. Baxter PJ. Medical effects of volcanic eruptions. Bull Volcanol. 1990;52:532‒544.