In biomedical studies the outcome of interest may be an ordinal, rather than a dichotomous, class label such as progression of disease. An example of an ordinal variable is drug toxicity levels evaluated as mild, moderate or severe. Another example is the Breast Imaging Reporting and Data System (BI-RADS)1 classification system. After a mammogram is read, a subjective score is assigned based on the condition of the breast tissue. These categories are: Category 0 - Incomplete; Category 1- Negative; Category 2 - Benign; Category 3 -Probably Benign; Category 4 - Suspicious Abnormality; Category 5 - Highly Suspicious of Malignancy; and Category 6 - Known Biopsy Proven Malignancy. The ordinality of these categories is evident. As another example, when cancer treatments are applied there is usually an interest in how patients respond. A typical way to measure this response is called the Revised Response Evaluation Criteria in Solid Tumors (RECIST).2 Based on a wide variety of tools, as well as defined rules for classification, Revised RECIST defines the responses as: Complete Response, Partial Response, Stable Disease, and Progressive Disease. The types of models used to model ordinal data include the multinomial, adjacent category logit, continuation ratio logit, proportional odds logit, stereotype logit, and cumulative link models.3 These models have the assumption, among others, that there are considerably more observations than variables. However, there are many types of data for which there are more variables than observations. When using microarray based, or other high throughout technologies, due to the expense of obtaining samples, there may be few observations but thousands of variables. The afore-mentioned models are not estimable by traditional means or without additional assumptions. Although there are data dimensionality reduction techniques, such as principle component analysis, due to the severely unbalanced nature of the data it may still be impossible to satisfactorily reduce the subset of variables to be less than the number of observational units without a significant loss of information in the data. This paper is concerned with the development of an ordinal classification model using the Least Absolute Shrinkage and Selection Operator (LASSO) and ridge penalizations to accommodate the case where there are considerably more variables than observations. This described procedure uses the stereotype logit model4 with the applied penalty in an attempt to overcome said problems. The proposed method is applied to simulated data. An algorithm is presented in which the above penalized likelihood is utilized to model high dimensional data with an ordinal outcome; the algorithm is applied to an actual data set with promising results.
Motivating example
The motivating example came from a study titled "Genes Involved in Viral Carcinogenesis and Tumor Initiationin Hepatitis C Virus-Induced Hepato cellular Carcinoma".5 The primary aim of this National Institutes of Health (NIH) grant funded project was to find genes related to: Hepato-cellular Carcinoma (HCC), a malignancy of the liver; and cirrhosis of the liver. Although the incidence of HCC is relatively low in developed countries, in the past few decades there has been an increase in the number of reported cases in countries such as Japan, the United Kingdom and France.6 The number of reported cases is al soon the rise in the USA and is due, in part, to the prevalence of the Hepatitis C Virus (HCV). It is estimated that 4,000,000 persons are HCV sero-positive and it is known that one of the main causes of HCC is HCV infection.7 In this study the issue of cirrhosis is also covered. Cirrhosis is a condition in the liver where the tissue is replaced by fibrosis, scartissue, and re-generative nodules. Like HCC, some of the causes of cirrhosis are HCV, Hepatitis B, and alcohol abuse.8 It is believed that almost every carcinogenic path way is altered in the development of the HCC.7 In the diagnosis of HCC the following guidelines are provided by:9 Once HCC is suspected, a computed tomography (CT) scan of the liver and thorax is a common detection mechanism. In addition, a magnetic resonance imaging (MRI), followed by a CT scan, may offer a more effective means of detecting lesions on the liver.
Once HCC has been successfully confirmed, transplantation is one of two successful methods proved at resolving this disease, along with hepatic resection.9 In the case where surgery is not possible, non-surgical techniques, such as percutaneous ethanol injection (PEI), may provide some benefit.9 In the case the cancer cannot be resolved; the disease usually results in death to the patient in approximately3-6months, although it has been common for some people to survive longer. Although there are ways and methods aimed at detecting this disease, HCC is usually caught in the later stages and there is still no set standard of care.9 In therefore mentioned study there were various diseased states of the liver.
The tissue types are:
- Normal liver tissue (normal)
- Cirrhotic liver tissue (pre-malignant)
- HCC liver tissue (malignant)
As stated by Thomas & Zhu7 Because of the heterogeneity of the under lying etiologies, it is a challenge to provide a clear and consistent portrait of the principal molecular abnormalities in this disease."Due to the complex nature of this cancer, some people believe that estimating HCC for HCV patients cannot be done with a given level of accuracy.11 The issue of diagnosis for HCC provides an excellent opportunity to evaluate our model framework as the proposed method will not only find genes related to HCC, but also to the progression of the disease based on the ordinal out come. There has been recent work on fitting a penalized model to a subset of the data from this study.12
The stereo type Logit model
The stereo type logit model was initially proposed by Anderson4 and is based on the multinomial distribution. For a given observation,
, denote the outcome vector, of length
,
as
where
if for that observation, the outcome is in the
category; the other entries in the vector are 0. There are
possible outcomes. In addition, the
level is defined as the reference level against which all other levels are compared. There is also a covariate vector
consisting of
covariates possibly related to the outcome. For the one dimensional stereo type logit the model has the log likelihood of
(1)
where
, (2)
and
. (3)
In addition
is represented as
, though
is now modeled as
. (4)
The baseline category, against which all others are compared, is the Jth level. For each ordered level the effect of the independent variables is equal to an overall effect multiplied by a value
. This is applicable when modeling disease progression where it is believed that a group of covariates are related to the disease and that this relationship is proportional for all levels. The intensity parameter,
, is used to determine the ordinal structure. That is, for
if
then outcome level
is higher than level
We can also determine whether there is a statistically significant difference between two levels based on their magnitude parameters. In a medical setting there may be case of a given diseased tissue, say lung tissue, having varied states. It may not be clear whether a given state is better or worse than another. In other words, there is no ordering among the states. The stereotype model has a direct appeal to this setting; as a preliminary analysis, researchers can gain insight into the ordering of the tissue states as well as whether there is a significant difference between two states previously considered to differ. As this is an ordinal model we are concerned with modeling the logits
The log likelihood is now represented as
.(5)
Elastic net constrained Stereo type Logit model
This model takes a multinomial likelihood, with a stereotype logit, and adds a penalty to it in an attempt to model high dimensional data. Currently, there is not a set standard method to analyze the discussed data structure employing a likelihood approach. The applied penalty is known as the elastic net penalty.13 A constraint on the sum of the absolute value of the parameters of interest is imposed. In addition, to ensure stability of the estimates, an additional smaller penalty on the sum of the squared values of the parameters is also enforced.13 For a set of parameters, represented in a
length vector
, the elastic net penalty is defined as follows
(6)
where
is allowed to vary, and
is a tuning parameter which ranges from 0 to 1.14 The value of
represents the proportion of the penalty attributed to the LASSO and
is the proportion of the penalty attributed to the ridge. The second term places a penalty on the sum of the absolute value of the parameters and is known as the LASSO penalty. This penalty has the effect of restricting the selected number of parameters to be less than the number of observations.15 In addition, this penalty leads to a theoretical unique solution when the objective function is convex.16 If this case does not hold, the first term of the penalty as defined on the sum of the squared values of the parameters17 becomes relevant. This term is known as the ridge penalty. Applying the ridge penalty alone yields an estimate for each covariate; the LASSO yields a parsimonious model forcing many parameters to 0. As such, the goal is that the LASSO penalty will have more effect than the ridge penalty. For the stereo type logit representation, there is a common underlying effect for each level of the ordinal outcome; it is the intensity of this effect that differs from level to level. Based on the multinomial distribution, we are concerned with finding a set of estimates for our parameters,
, such that
(7)
where
denotes the vector of length J-1 containing the intercepts for the J-1 logits, and
denotes the vector on length J-1 containing the intensity parameters. In addition, the intensity parameters,
, are bounded such that
for .4 We note that minimizing the negative log likelihood is equivalent to maximizing the log likelihood. Therefore, after imposing the elastic net constraints, we are concerned with finding parameter estimates such that:
.(8)
The goal is to emphasize the LASSO penalty over the ridge. For our research, as
is allowed to vary, there is a desire to trace the corresponding solutions of our nonlinear objective function through this parameter. In addition to specifying the starting value of
, the maximum penalty,
, needs to be specified. Additionally, the step length is defined as the distance between adjacent values of our varying penalty parameter
, or
. Termination criteria must also be specified. This concept of tracing the solution through the given parameter is formally referred to as the
trace.15 An approach aimed at modeling our nonlinear objective function with the elastic net constraint is now presented and is based on an approach employed by Park and Hastie.15 An implemented algorithm based on the modeling approach is subsequently presented.
Implemented algorithm
The implemented algorithm attempts to model equation (5) over the
trace. This approach utilizes nonlinear programming to find optimal solutions for a given value of
. This algorithm gives the user control over the range of
values. The user is allowed to select
,
, and
. The parameter
is set at a fixed parameter over
and is now denoted
. The general algorithm describes the application of modeling procedure over the
trace and is called lambda trace; leading to numerous models being fitted. For a given value of
, a sub-algorithm is invoked; we call this procedure model estimation. This sub-algorithm uses an optimization algorithm developed by Ye18 in model fitting. For the model estimation, the entry order of the variables into the model needs to be specified, the procedure variable entry into the model performs this step.
The lambda trace algorithm is now presented.
Lambda trace algorithm
- Determine the smallest value of
,
. This is selected by the user.
- Determine the largest value of
,
. This is selected by the user.
- Determine
, the step length. This is selected by the user
- Calculate the number of models to be fit. This is calculated as
and is denoted as
.
- Set
- For
invoke the procedure model fit to find the solution. Denote the solution at k
- If
, terminate, else set
and repeat step 6.
The above procedure is responsible for providing and storing the parameter estimates for all models along the
trace. The benefit of having the user selects
,
and
is that the solution can be tailored for specific circumstances. If there is a desire to highly penalize the model so that only a few covariates will be included, or to place a lower range of penalty on the model so that a larger amount of covariates will enter the model, or evaluate a larger range of models,
,
can be selected accordingly. Also if
is smaller the fitted models will be closer with regards to the parameter estimates; a larger version of
will result in models where the parameter estimates could be more varied. This approach allows more flexibility with respect to the execution of the algorithm. In addition, define the active set A, as the set of covariates that are included in the solution at
.The algorithm model estimation, which is used to provide a solution at a set value of
, is now presented.
Model estimation algorithm
- Determine the order of entry of the variables into the model using the model entry procedure. Denote this list of entry as the vector of length ,
. Include the first 5 important variables in the preliminary model. Set
.
- Use nonlinear programming to find the solution to equation (5), for a given value of
. Denote the set of parameter estimates at this stage
, t=1,2,… .For the parameter estimates
if
, then it is removed from the model.
- If the length of
is
or if all variables in
have been considered then go to step 5, else include the next important variable, as determined by
, set
, and repeat step 2.
- Among the candidate models choose the one which has the best classification performance (the one with the highest percent correctly classified). For the given value
denote this model as
This algorithm attempts to model the nonlinear objective function subject to the elastic net penalty at a given value of
. Before the variables are passed to this algorithm they are scaled and centered. In addition, as the whole aim of this paper is to correctly model and classify ordinal outcome data with a high and complex covariate space, the sub model that correctly determines the highest proportions of correctly classified outcomes is selected. As the multinomial log likelihood model, with the stereotype logit representation, is a generalized nonlinear model, adequate starting values must be determined. Once the order of entry has been determined by the model entry procedure, the first five entries are input and the model is fit. Each literation includes the next important variable in
. For a given iteration
, a parameter estimate is removed if
where
is a user adjusted parameter with the default of
. It is desirable that parameter estimates with values close to 0 be removed from the model; therefore
should be set to a small value. This process continues until the maximum number of variables is
, or until all variables have been considered.
The variable entry into the model procedure, used to create
is now explained.
Variable entry into the model algorithm
- Discretize all continuous variables.
- For a variable, compute its minimum (min) and maximum (max) values.
- For a specified number of bins, calculate interval width as follows (max-min)/(number of bins). By default they are 4 bins.
- Place the variables into corresponding bin and return the bin number (1, 2, 3, or 4)
- For the newly created ordinal variables, calculate the gamma statistic19 using the ordinal outcome variable. Rank the variables in order of importance based on the absolute value of the statistic.
Applied bootstrap resampling procedure
For our model we need to estimate the standard errors of our parameter estimates. For the purposes of this paper, the bootstrapping pairs design is used.20 Denote B as the number of bootstrap re-samples. The size of B is set to 200; this is based on the fact that B ranging from 50 to 200 is sufficient.21 For a covariate matrix
and an ordinal outcome vector
, which are viewed as the population, define the tuple
which denotes the ith entry and row respectively,
. For each bootstrap resample we take a sample of n tuples, with replacement from the original data giving rise to a new data set
and
,
. Once we have the B re-samples, the corresponding model is fit to each data set. For the original data, once the model is selected based on the elastic net penalty, the corresponding value of
is used in model fitting for all bootstrap re-samples. This value is fixed as allowing it to vary may introduce additional variation into our model22 and it is desirable that the variances be correctly attributed to the parameters and their interactions with each other. Once the B models are fit the corresponding parameter estimates are obtained.
Denote the bth bootstrap parameter estimates as
. Having these B parameter estimates allow us to gain insight into the distributions of the parameter estimates as well as construct confidence intervals. The potential of using a bootstrap re-sampling procedure to obtain the distribution for a given parameter is that it no longer has to conform to a known form; it is no longer bounded. In addition, the corresponding confidence intervals can be developed; they need not be symmetric. The resulting B estimates for a given parameter can also be used to assess significance; by the proportion of them that are non-zero. In addition, a covariance matrix will also be calculated from the bootstrap re-samples. In the construction of the confidence intervals the bootstrap-t confidence interval method is used. In short, the bootstrap-t confidence intervals are of the from
(9)
where
(10)
with
being defined as
(11)
where
and
. (12)
In addition
is chosen from the standard normal distribution such that
(13)
where
is defined as
(14)
Model selection criteria
As the proposed modeling procedure leads to a group of models along the
trace, there is a need to select one model using objective criteria; different criteria may lead to different candidate models. The goal of any modeling procedure is to approximate, or make an educated guess at, the truth. The goal is to select models that will shed some light on the true phenomenon in the data. In this section three model selection procedures are employed; model selection based on Akaikie information criterion (AIC) and Bayesian information criterion (BIC) and cross validation using a data set. This may lead to the selection of up to three models for further consideration. For model selection, using AIC and BIC, once the corresponding models along the
trace are found the model yielding the lowest AIC and BIC value are selected. In applying these criteria the log likelihood in equation (5) is used; the penalty is not included. As these model selection procedures are calculated using non-penalized likelihoods, not pseudo-log likelihood like that in equation (8), it is best to adhere with convention.8 In practice AIC has a tendency to select models that include a larger number of variables, some of which are truly unimportant.24 Model selection, using BIC, leans towards models that select fewer covariates as compared with AIC.25
The third approach selects the ideal model based on its predictive capabilities. The modeling procedure is used to obtain various models for values of
along the
trace; their performance is evaluated on a given data set. For the ordinal outcome data, a simple definition of classification performance is employed and is defined as follows: divide the number of correctly classified observations by the total number of observations. The model that is able to correctly classify the most observations is selected. For this paper, validation was performed using the data to which the model was fit. Once our three candidate models have been selected, they can be compared using various objective measures.
Data simulation
For assessing the proposed model the multivariate normal distribution was used to simulate datasets consisting of a large number of covariates and a smaller number of samples, such as is the case with microarray gene expression data. For each simulation, N=80 observations and P=400 covariates were generated. The correlation matrix is of dimension 400×400. The correlation matrix has a compound symmetric structure where the off diagonal entries, ρ, equal 0.01. This structure was selected to test the strength of the proposed modeling scheme against different relationships among the covariates. After the full correlation matrix was created, to make its form acceptable for further processing the correlation matrix was converted to its positive definite form. Thereafter, ten covariates were selected to be the truly important predictors by setting their corresponding coefficient values to either 0.5 or -0.5. The remaining 390 covariates were not related to the response and hence were unimportant to the predictive structures; their coefficient values were set to 0. After this, the correlation matrix was converted to a variance matrix
.
Using the Cholesky’s decomposition the covariance matrix can be decomposed as follows:
(15)
Then, a matrix of dimension 400×80, denoted
, was generated so that the columns of the matrix demonstrate an independent multivariate normal distribution. An intermediate covariate matrix
with the desired covariate structure was created by the following transformation:
.(16)
Following this, a random normal vector, of length 390, with parameters N (0, 1) was generated to represent the means of the unimportant variables; the means of the 10 important variables correspond to a random normal vector whose entries are generated from N (6, 1). These combined vectors were used to represent the mean of the 400 covariates. The mean vector,
, was then combined with the covariate matrix to create the final covariate matrix
as follows,
(17)
Where
is 400×80 matrix with each column equaling
. For the desired outcome there are four levels. After the 10 truly predictive covariates were selected, the matrix
was generated.
is a 80×40 matrix containing the output row vectors, of length 4, for the 80 observations. Let i = 1,2,…,80 index the observations and j = 1,2,3,4 index the outcome levels. The probabilities
were generated using the stereotype logit model [4].
The simulated parameters for
contain {0.5, 0.5, 0.5, 0.5, 0.5, -0.5, -0.5, -0.5, -0.5, -0.5}. The baseline level was set at j=4. The simulated α parameters are {-0.7, -0.1, 0.1, 0.0}. The ϕ parameters values are {1.00, 0.67, 0.33, 0}. For a given observation, i, denote the true outcome, hi, as
. Denote the vector containing these values as
.The proposed modeling scheme was applied to
and
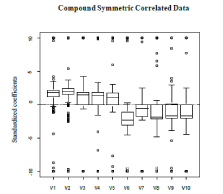
. Bootstrapping re-sampling techniques were used to estimate the 95% confidence intervals of the model parameters. The variable selection capabilities are acceptable as all 10 variables are selected in the final model. However, a large portion of the non-significant variables were included in the final model, 152 to be exact. Based on Figure 1 the signs of the estimates are correct. The first five should have a positive average value and the last five should be negative; this is preserved. For the confidence intervals of the parameter estimates, the intervals are somewhat small. This is the anticipated result as the proposed method is supposed to yield parameter estimates with low variability. This is seen in Table 1. The results indicate that the modeling framework is adept at variable selection; the classification capabilities require finer tuning.
Application to liver data
In the application of the method the only independent variables used were gene expression values. The cRNA samples were hybridized to the HG-U133A and the HG-U133A2.0. Chips. These chips are able to measure approximately 17000 and 14500 unique genes respectively (Affymetrix, CA).26 The raw data, CEL files were downloaded from http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE14323. The expression summaries were obtained using the robust median average (RMA). In an attempt to filter the genes the MAS 5Present/Absent calls were used. The only genes included were those for which there was a present call in all the samples.
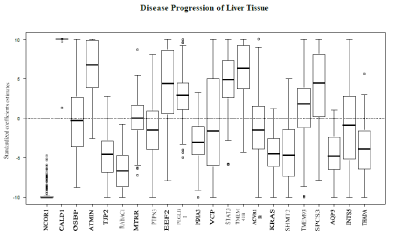
The proposed model was applied to the gene expression data set, with associated ordinal outcome, in an attempt to determine genes associated with disease progression of liver tissue classified by normal-cirrhosis-HCC. The algorithm lambda trace was formally applied to the data. The gene expression values were the only variables used. The variables were standardized (centered and scaled) prior to model fitting. Among the 98 samples, 19 had normal liver tissue, 41 had cirrhosis of the liver and 38had HCC. The genes used to fit the model were selected if the MAS 5calls were declared as present in all samples. MAS 5calls are used to remove the genes that cannot be detected with a given degree of reliability. If, for a given gene, the MAS 5 called is present then the readings for this gene are reliable. This reduced the number of candidate genes to 4406; this set was passed to the model building process. The results are shown for the model corresponding to λ=0.001.