eISSN: 2378-315X


Research Article Volume 7 Issue 1
Caesar Kleberg Wildlife Research Institute, Texas A&M University Kingsville: Kingsville, USA
Correspondence: David B Wester, Caesar Kleberg Wildlife Research Institute, Texas A&M University Kingsville: Kingsville, Texas, USA
Received: January 21, 2018 | Published: February 27, 2018
Citation: Wester DB. Comparing treatment means: overlapping standard errors, overlapping confidence intervals, and tests of hypothesis. Biom Biostat Int J. 2018;7(1):73?85. DOI: 10.15406/bbij.2018.07.00192
Many applied disciplines report treatment means and their standard errors (or confidence intervals) in the presentation of experimental results. Often, overlapping standard error bars (or confidence intervals) are used to draw inferences about statistical differences (or lack thereof) between treatments. This practice can lead to misinterpretations about treatment effects because it lacks type I error rate control associated with formal hypothesis tests. Theoretical considerations and Monte Carlo methods are used to show that the probability that standard error bars overlap is affected by heterogeneity of variances in an unpaired data collection setting; in a paired setting, this probability is affected by heterogeneity of variances, degree and direction of non—independence (covariance) between treatments, and the variance of random pairing effects. As a result, basing inferences on overlapping standard error bars is a decision tool with type I error rates ranging from 16% to 32% in an unpaired setting, and from 0% to 32% in a paired setting. In contrast, type I error rates associated with overlapping 95% confidence intervals are at most 5% and generally much smaller. These considerations apply to one— and two—sided tests of hypotheses. In multivariate applications, non—overlapping hypothesis and error ellipses are reliable indicators of treatment differences.
Keywords: P value, treatment mean comparison, type I error rate
There are several different philosophical/methodological approaches commonly used in the applied disciplines to investigate effects under study in designed experiments. In a letter to Jerzy Neyman (12 February 1932), Fisher1 wrote, “. . . the whole question of tests of significance seems to me to be of immense philosophical importance.” And in 1929, Fisher2 wrote:
“In the investigation of living beings by biological methods statistical tests of significance are essential. Their function is to prevent us being deceived by accidental occurrences, due not to causes we wish to study, or are trying to detect, but to a combination of many other circumstances which we cannot control.”
Little3 provided a conceptual history of significance tests and Stephens et al.4 documented its prevalence in ecology and evolution. Salsburg5 wrote that, ‘. . . hypothesis testing has become the most widely used statistical tool in scientific research,’ and Lehmann6 suggested that t and F tests of hypotheses ‘today still constitute the bread and butter of much of statistical practice.’ Criticism of null hypothesis significance testing also has a long history7. Robinson & Wainer8 observed that as the number of criticisms of this approach has increased so has the number of defenses of its use increased.4,9
In addition to null hypothesis testing, the importance of ‘effect size’ was recognized early as well. Deming10 wrote that, ‘The problem is not whether differences [between treatments] exist but how great are the differences . . . .’ Numerous authors have encouraged more attention to effect size estimation.11 Bayesian methods12 that include credibility intervals13 and multi—model selection14 also have been offered as alternatives to null hypothesis testing.
Each of these approaches has strengths and weaknesses which should be appreciated in order to most effectively use them to address a research hypothesis—and it is not the intent of this paper to enter into this discussion. My goals are more modest: to clarify that
Consider an experiment designed to compare weight change of animals on several different rations. If animals are relatively homogeneous (similar initial weight, etc.) then a completely randomized design can be used; alternatively, variability in initial weight can be blocked out in a randomized block design. In either case, a significant F test on treatment mean equality often is followed up with pairwise comparisons among treatments.
One of the most common ways to present results from an experiment designed to compare two or more treatments is to graph or tabulate their means. Presenting treatment means without also presenting some measure of the variability associated with these estimates, however, is generally considered ‘telling only half of the story.’ It is usually recommended, therefore, to present treatment means together with their standard errors or with confidence intervals. Interpretation of these measures of variability must be done carefully in order to properly understand the effect of the treatments.
Data from these kinds of studies can be analyzed and presented in several ways (Figure 1). We might report that mean weight change in the control diet was = 11 lbs whereas mean weight change in the experimental diet was = 25 lbs (Figure 1a). If only treatment means (i.e., point estimates) are presented e.g.,15, critical information—in particular, a measure of the variability associated with these estimates—is missing. Clearly, the findings of this experiment can be enriched with a more complete presentation.
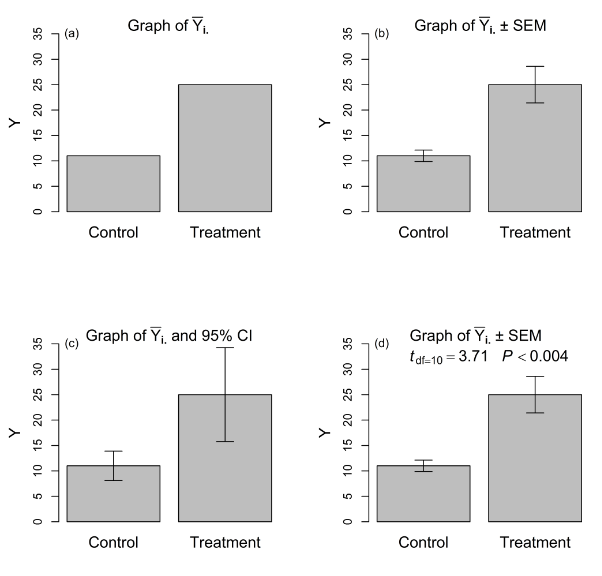
Figure 1 Four ways to present results from an experiment designed to compare the equality of means in two treatments: (a) treatment means only; (b) treatment means and standard error bar for each mean; (c) treatment means and confidence interval for each mean; (d) treatment means, standard error bar for each mean, test statistic (with df) for hypothesis of treatment mean equality, and P-value associated with test statistic.
Consider what is gained by providing standard errors together with treatment means (Figure 1b). If we reported = 11 ± 1.1 lbs and = 25 ± 3.6 lbs, our colleagues likely would nod in approval. In contrast, if we reported = 11±9 and = 25±13 lbs, the high variability might call into question our experimental technique, or at least raise questions about the homogeneity of our experimental material—and providing standard errors allows a reader to make such assessments. So far, this approach involves providing standard errors for descriptive purposes only.
However, some researchers draw conclusions about treatment differences based on whether or not the standard errors around the treatment means overlap. For example, Beck et al.16 wrote, ‘Non—overlapping standard errors were used as evidence of significant differences . . . among [treatments].’ Jones et al.17 wrote, ‘Significant difference . . . between [treatments] . . . was determined by non—overlapping standard errors.’ Wisdom & Bate18 wrote that ‘. . . we found no difference (overlapping standard errors) . . . [between treatments].’ And Dwan´isa et al.19 wrote that ‘It bears mentioning that the error bars overlap thus indicating that [the response variable] may be the same in both [treatments].’ Huang et al.20 wrote that ‘we remind the reader that for two [treatments] whose standard errors overlap, one may conclude that their difference is not statistically significant at the 0.05 level. However, one may not conclude, in general, that [treatments] whose standard errors do not overlap are statistically different at the 0.05 level.’ Finally, some authors evidently consider a non—significant analysis of variance F test and overlapping standard error bars as synonymous: ‘Each of the ANOVA models. . . was non—significant, bearing out the impression of stability suggested by overlapping standard error bars around these means’.21
A little reflection suggests an immediate difficulty: if our standard errors do not overlap and we choose to declare a difference between treatments, what ‘P’ value should we attach to our inference? After all, there is nothing in the calculation of two treatment means and their standard errors that involves any use of the usual tabular t or F distributions.
Some researchers present treatment means and corresponding confidence intervals estimated for each mean. In our example, we might report that = 11 (95% CI: 8.1, 13.9) and = 25 (95% CI: 15.7, 34.3) (Figure 1c). Of course, a confidence interval is simply a treatment mean with a “± ‘scaled’ standard error” (where the scaling factor is the appropriate value from Student’s t distribution), but it carries with it the added inferential information of an interval estimate—which can be adapted to the researcher’s needs by the selection of an alpha level—about each treatment mean that the standard error alone lacks.
As with standard errors, some scientists compare treatments by examining the overlap of confidence intervals estimated around each treatment. This inference may be only implicit. For example, ‘Estimated species richness was 38 (95% CI: 30.1—46.2) at undiked sites compared to 33 (95% CI: 29.2—36.7) at diked wetlands, but the confidence intervals overlapped considerably’;22 ‘Despite the reduction in coyote predation rate during 2010, non—coyote—predation rate did not increase (95% CIs overlapped extensively) . . .’. 23 More explicitly, Mantha et al.24 wrote, ‘When two means based on independent samples with more than 10 observations in each group are compared, and the 95% CIs for their means do not overlap, then the means are significantly different at P < 0.05.’ Bekele et al.25 applied this approach to medians: ‘When the 95% confidence intervals of the medians overlap, the medians being compared were considered statistically not different at 5% probability level; otherwise the medians were considered statistically different.’ In contrast to the approach of comparing the overlap of standard errors, we will see that this approach is actually quite conservative, with a type I error rate generally much lower than 5% when 95% confidence intervals are estimated.
The most rigorous and complete analysis and presentation provides treatment means, their standard errors (or confidence intervals), and results from a formal test of hypothesis of treatment mean equality (Figure 1d); we would report that ‘ = 11 ± 1.1 lbs and = 25 ± 3.6 lbs, = 3.72, P < 0.004.’ This is the only inferential approach (for our experimental designs) that operates at the nominal alpha level. This approach is equivalent to estimating a confidence interval around the difference between two treatment means and comparing it to a value of zero.
In this paper, I explore the interpretation of overlapping standard errors, overlapping confidence intervals, and tests of hypothesis in univariate settings to compare treatment means. These principles, usually laid down in introductory courses in biometry, biostatistics and experimental design, are of course understood by statisticians. As the selected quotations above illustrate, however, these basic principles are often overlooked or misunderstood by applied scientists, and the resulting confusion about what is ‘significant’ (or not) in an experiment can have far—reaching implications in the interpretation of scientific findings. Simulation methods are used to illustrate key concepts. Results of Payton et al.26,27 for unpaired settings are confirmed; new results are provided for paired samples which also incorporate the influence of random effects (resulting from pairing); one—sided hypothesis tests are considered; and experiment—wise error rates for experiments with more than two treatments are considered.
For each of N = 10, 000 simulated data sets, pseudo—random samples of size n = 5, 10, 20, 30, 50, 100, or 1,000 were generated for each of t = 2 populations (treatments) for which . For a completely randomized design, the linear (fixed effects) model is
(1)
and = 0 when . Population standard deviations were set at (1) , or (2) . A confidence interval around a treatment mean is , where and
. For a randomized block design, the linear (mixed effects) model is
(2)
i = 1, 2; j = 1, 2, . . . , n; and when ; the random effect, , is responsible for pair—to—pair variation (i.e., the random ‘block’ effect). Population standard deviations were set at ; population covariances between treatments were set at ; and . A confidence interval around a treatment mean is where and = .
The proportions of standard errors bars and confidence intervals that overlapped were counted in the N = 10, 000 simulated data sets for each experimental design. Also, for each data set, the hypothesis vs was tested. For the completely randomized design, this hypothesis was tested with an unpaired t test: , where is the error mean square from an analysis of variance with expectation , the pooled error variance28; was compared to a tabular Student’s t value, for the case of homogeneous variances and to where 29 for the case of heterogeneous variances. For a randomized block design, this hypothesis was tested with , where is the error mean square for the analysis of variance with expectation 30 where ; was compared to a tabular t value, . (The difference in notation— for a CRD and for an RBD—reflects the different assumptions for these two experimental designs: in a CRD variances within treatments are assumed to be homogenous and are pooled whereas in an RBD variances within treatments are not assumed to be homogenous and are averaged.)
Treatment means were compared using three distinct approaches:
Approach A: standard errors were estimated for each treatment mean and inferences were based on the proportion of overlapping standard errors from the N = 10, 000 simulated data sets.
Approach B: (1−α)100% confidence intervals were estimated for each treatment mean and inferences were based on the proportion of overlapping confidence intervals from the N = 10, 000 simulated data sets and
Approach C: a test of the hypothesis, hypothesis vs . For the CRD, an unpaired t test was used with error df when variances were homogeneous and Satterthwaite’s adjustment when variances were heterogeneous; for the RBD, a paired t test with error df was used.
Theoretical considerations
For an unpaired setting (eq. 1), the probability that confidence intervals around two treatment means overlap is Payton et al.27
(3)
where is the upper quantile of Student’s t distribution with df. After rearrangement, eq. 3 is
(4)
One of the terms in eq. 4 is . When data are collected in an unpaired setting (eq. 1), the standard error of is estimated by. Thus, if we divide eq. 4 by , and then recall that , eq. 4 can be written as
(5)
Replacing the tabular t (eq. 4) or F (eq. 5) with the value of ‘1’ yields the probability of overlapping standard errors. The large sample probability that standard errors around two means overlap is
(6)
where is the cumulative standard normal distribution. The large sample probability that two confidence intervals overlap (cf Goldstein & Healy31) is obtained by multiplying the term in square brackets in eq. 6 by , the upper quantile of the standard normal distribution.
Afshartous & Preston32 studied this problem in situations with ‘dependent data’ (i.e., paired samples); their approach, however, was limited to cases involving a fixed effects model. In paired settings, it is usually the case that the basis for pairing represents a random nuisance variable, and so a mixed model (eq. 2) is generally more appropriate in most applications. To extend these considerations to a paired setting with a random nuisance effect, we note that the standard error of a treatment mean, , is
, where is estimated by Thus, eq. 3 becomes
(7)
and eq. 4 becomes
(8)
In a paired setting (eq. 2), the standard error of is estimated by . Thus, we divide eq. 8 by and eq. 5 becomes
(9)
The large sample probability that standard errors around two means overlap in a paired setting is
(10)
where is the cumulative standard normal distribution. Multiplying the term in square brackets in eq. 10 by gives the large—sample probability that two confidence intervals overlap.
Monte carlo results: unpaired t test (CRD)
Each time in the Monte Carlo simulation, when two confidence intervals overlapped it was also true that was less than (Table 1), providing empirical support for the simulations. A similar conclusion applies to incidences of overlapping standard errors and (eq. 5 with the tabular F replaced with the value of ‘1’).
Sample size |
Standard errors |
Confidence intervals |
t Test |
|
|
|
|
|
|
Homogeneous variances: |
|
5 |
0.7847 |
0.9952 |
0.9503 |
10 |
0.8161 |
0.9936 |
0.9468 |
20 |
0.8310 |
0.9941 |
0.9503 |
30 |
0.8327 |
0.9941 |
0.9478 |
50 |
0.8369 |
0.9949 |
0.9523 |
100 |
0.8399 |
0.9952 |
0.9513 |
1000 |
0.8492 |
0.9950 |
0.9491 |
Asymp |
0.8427 |
0.9944 |
0.9500 |
Sample Size |
Standard Errors: |
Confidence Intervals: |
t Test: |
|
|
|
|
|
|
Heterogeneous variances: |
|
5 |
0.7146 |
0.9813 |
0.9456 |
10 |
0.7424 |
0.9841 |
0.9471 |
20 |
0.7603 |
0.9815 |
0.9482 |
30 |
0.7678 |
0.9827 |
0.9510 |
50 |
0.7627 |
0.9849 |
0.9496 |
100 |
0.7688 |
0.9836 |
0.9486 |
1000 |
0.7758 |
0.9841 |
0.9523 |
Asymp |
0.7748 |
0.9825 |
0.9500 |
Table 1 Summary of N = 10,000 Monte Carlo simulations of a completely randomized design with two treatments (with) (unpaired t test, ). Values in the table are the relative frequency of overlapping standard errors or overlapping 95% confidence intervals and the relative frequency that or | were less than indicated critical values with or degrees of freedom. Asymptotic values are from eq. 6. Type I error rates are 1 – tabulated values
When variances are equal, the term is equal to and the probability that standard errors overlap (eq. 6) reaches its maximum value of P = 0.8427 (corresponding with a type I error rate of about 16%), illustrated in Table 1 with increasing sample size. With unequal variances, the probability that standard errors overlap decreases and the type I error rate increases; Table 1 illustrates this when , in which case the probability of overlap decreases to ~77.58% (and the type I error increases to about 23%) with increasing sample size. As the difference between variances increases, approaches 1, and the probability that standard errors overlap approaches a value of 68.27% (corresponding to a type I error rate of ~32%; (Figure 2). In contrast to results based on overlapping standard errors, the frequency of overlapping 95% confidence intervals approached 99.44% (0.56% type I error rate) with homogeneous variances and 98.25% (1.75% type I error rate) when (Table 1). With increasing heteroscedasticity, the probability that two confidence intervals overlap approaches 95% (a type I error rate of 5%) with large sample sizes.
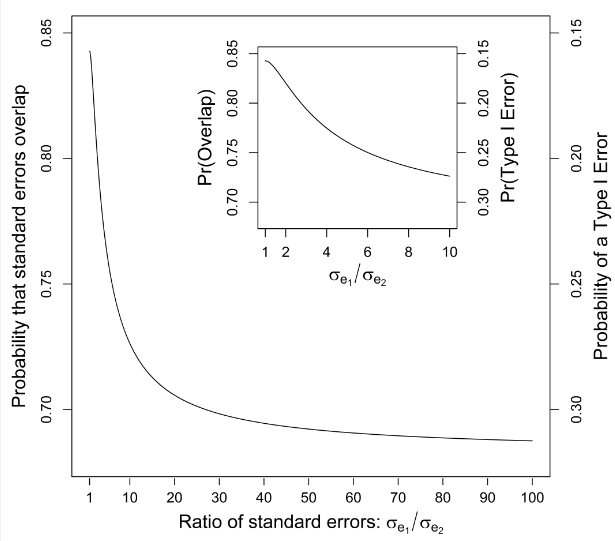
Figure 2 Relationship between the probability that standard errors around two treatment means (when ) collected in an unpaired setting overlap (as well as the associated type I error rate) as a function of the ratio of the standard errors of each mean, , ranging from 1 to 100. Inserted figure:, ranges from 1 to 10.
Monte carlo results: paired t test (RBD)
Overlapping confidence intervals in the Monte Carlo simulation in a paired setting coincided with being less than ; a similar conclusion applies to the overlap of standard errors (Table 2).
Sample size (n) |
Standard errors |
Confidence intervals |
t Test |
||||||||||||||
|
|
|
|||||||||||||||
|
|
|
|||||||||||||||
0 |
4 |
16 |
0 |
4 |
16 |
0 |
4 |
16 |
|||||||||
Variance-covariance structure: |
|||||||||||||||||
5 |
0.7966 |
0.8386 |
0.9047 |
0.9949 |
0.9976 |
0.9987 |
0.9506 |
0.9506 |
0.9506 |
||||||||
10 |
0.8189 |
0.8621 |
0.932 |
0.9952 |
0.9982 |
0.9996 |
0.9513 |
0.9513 |
0.9513 |
||||||||
20 |
0.8291 |
0.8732 |
0.9429 |
0.9951 |
0.9977 |
1 |
0.9455 |
0.9455 |
0.9455 |
||||||||
30 |
0.83 |
0.8749 |
0.9428 |
0.9944 |
0.9986 |
1 |
0.9454 |
0.9454 |
0.9454 |
||||||||
50 |
0.8321 |
0.8784 |
0.9465 |
0.9932 |
0.9972 |
0.9999 |
0.9485 |
0.9485 |
0.9485 |
||||||||
100 |
0.8442 |
0.8857 |
0.9556 |
0.9949 |
0.9985 |
0.9999 |
0.9526 |
0.9526 |
0.9526 |
||||||||
1000 |
0.8431 |
0.8855 |
0.9541 |
0.9946 |
0.9982 |
0.9999 |
0.9498 |
0.9498 |
0.9498 |
||||||||
Asymp |
0.8427 |
0.8862 |
0.9545 |
0.9944 |
0.9981 |
0.9999 |
0.95 |
0.95 |
0.95 |
||||||||
Variance-covariance structure: |
|||||||||||||||||
5 |
0.8487 |
0.8818 |
0.9361 |
0.9981 |
0.999 |
0.9995 |
0.9521 |
0.9521 |
0.9521 |
||||||||
10 |
0.8738 |
0.9076 |
0.9596 |
0.9986 |
0.9993 |
0.9999 |
0.9519 |
0.9519 |
0.9519 |
||||||||
20 |
0.8852 |
0.9214 |
0.9678 |
0.9984 |
0.9994 |
1 |
0.9472 |
0.9472 |
0.9472 |
||||||||
30 |
0.883 |
0.9227 |
0.9722 |
0.9987 |
0.9996 |
1 |
0.9476 |
0.9476 |
0.9476 |
||||||||
50 |
0.89 |
0.9245 |
0.9736 |
0.9978 |
0.9995 |
1 |
0.9478 |
0.9478 |
0.9478 |
||||||||
100 |
0.8949 |
0.9345 |
0.98 |
0.9988 |
0.9993 |
1 |
0.9533 |
0.9533 |
0.9533 |
||||||||
1000 |
0.8962 |
0.9318 |
0.9807 |
0.9988 |
0.9999 |
0.9999 |
0.9508 |
0.9508 |
0.9508 |
||||||||
Asymp |
0.8975 |
0.9321 |
0.9791 |
0.9986 |
0.9997 |
0.9999 |
0.95 |
0.95 |
0.95 |
||||||||
Variance-covariance structure: |
|||||||||||||||||
5 |
0.7467 |
0.7987 |
0.878 |
0.9914 |
0.9954 |
0.9977 |
0.9501 |
0.9501 |
0.9501 |
||||||||
10 |
0.771 |
0.8196 |
0.9047 |
0.9995 |
0.9938 |
0.999 |
0.9502 |
0.9502 |
0.9502 |
||||||||
20 |
0.7767 |
0.829 |
0.9108 |
0.9881 |
0.995 |
0.9991 |
0.9465 |
0.9465 |
0.9465 |
||||||||
30 |
0.778 |
0.8277 |
0.9127 |
0.9869 |
0.9958 |
0.9995 |
0.9456 |
0.9456 |
0.9456 |
||||||||
50 |
0.7807 |
0.8312 |
0.9163 |
0.9855 |
0.9931 |
0.9997 |
0.9486 |
0.9486 |
0.9486 |
||||||||
100 |
0.7907 |
0.8439 |
0.9263 |
0.9876 |
0.9949 |
0.9993 |
0.9518 |
0.9518 |
0.9518 |
||||||||
1000 |
0.797 |
0.8436 |
0.926 |
0.987 |
0.9944 |
0.9998 |
0.9497 |
0.9497 |
0.9497 |
||||||||
Asymp |
0.7941 |
0.8427 |
0.9264 |
0.9868 |
0.9944 |
0.9996 |
0.95 |
0.95 |
0.95 |
||||||||
Table 2 Summary of N = 10,000 Monte Carlo simulations of randomized block design with two treatments (with ) (paired t test, ). Values in the table are the relative frequency of overlapping standard errors or overlapping 95% confidence intervals and the relative frequency that or were less than indicated critical values with . Asymptotic values are from eq. 10. Type I error rates are 1 – tabulated values
In the expression for the probability that two standard errors overlap for paired sampling (eq. 10), the term reaches a minimum value equal to 1 when , and the covariance, , is negative but such that (the latter condition to ensure that ∑, the variance—covariance matrix, is positive definite), and under these conditions the probability that two standard errors overlap reaches its minimum value of approximately 68% (corresponding to a type I error rate of about 32%; (Figure 3). With homogeneous variances between treatments and , the probability that standard errors overlap increases to its maximum value of 100% (corresponding to the 0% probability of a type I error) when the covariance between treatments is positive and .
The term in eq. 10 also increases beyond its minimum value when variances within treatments are heterogeneous () and/or and/or (with ∑ positive definite), under which conditions the probability that standard errors overlap increases and can approach 1. These general conditions are illustrated in Table 2 for 3 specific combinations of variances within treatments and covariances between treatments as well as 3 values for the block variance. Figure 3 illustrates a scenario where the probability of overlapping standard errors extends across its range of ~68% to ~100%—when variances within treatments are homogeneous, the block variance equals 0, and the covariance between treatments, , varies—as well as selected cases when are unequal and . As with the unpaired setting, the type I error rate for the paired t test is approximately 5% regardless of sample size, the variances and covariances of errors, or the variance of the block effect.
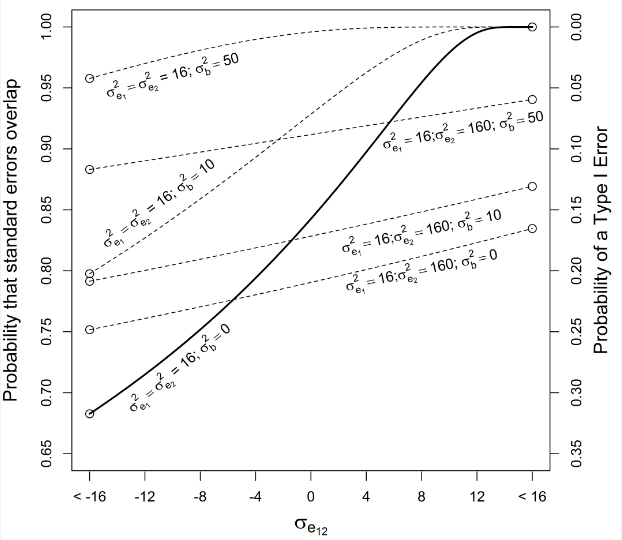
Figure 3 Relationship between the probability that standard errors around two treatment means (when ) collected in a paired setting overlap (as well as the associated type I error rate) as a function of the covariance between treatments for several combinations of within-treatment variances, , and block variance, .
Regarding one—sided tests
A confidence interval is simply a ‘scaled’ standard error. Meehl et al.33 argued that non—overlapping scaled standard error bars, , where , is equivalent to a one—sided —level t test of the difference between two means. It should be noted that the df of their tabular Student’s t statistic correspond with the error term in an unpaired setting (and are therefore different from the df in eq. 3); additionally,
, as defined by Meehl et al.33 is a standard deviation rather than a standard error. That is, they suggested that < is equivalent to rejecting in favor of with a one—sided —level t test. This is incorrect. Even when a standard error, , is used, the asymptotic probability that two such scaled standard error bars overlap is
(11)
Thus, with , this probability approaches only when are very different (and approaches 1); and this probability approaches 0.99 when variances between treatments are equal, leading to a type I error rate ~1% rather than ~5%.
Concerning experiment—wise and comparison—wise error rates
The foregoing dealt with experiments that involved two treatments. When an experiment involves more than two treatments and the overall research objectives include all possible pairwise comparisons among treatments, the investigator should be concerned with the distinction between experiment—wise and comparison—wise error rate. There are many available tests.
A commonly—used analytical strategy, the protected (or Fisher’s) Least Significant Different test (FLSD), involves an initial —level F test of overall treatment mean equality. When this F test is not significant then pairwise comparisons are not made; when the initial F test is significant, then all possible pairwise comparisons are made with an —level t test. The initial F test controls the experiment—wise error rate at and the comparison—wise error rate is less than ![]() when the initial F test is used to guide whether or not pairwise comparisons are performed. If, however, all possible pairwise comparisons are made with an —level t test without first performing the initial F test (LSD), then although the comparison—wise error rate = the experiment—wise error rate > (and increases as the number of treatments increase).
when the initial F test is used to guide whether or not pairwise comparisons are performed. If, however, all possible pairwise comparisons are made with an —level t test without first performing the initial F test (LSD), then although the comparison—wise error rate = the experiment—wise error rate > (and increases as the number of treatments increase).
To illustrate these principles, a completely randomized design with t = 5 treatments, n = 30 replications and homogeneous variances of experimental errors was used with N = 10,000 Monte Carlo simulations in which population treatment means were equal. The initial F test was significant in 511 of the 10,000 experiments, confirming an experiment—wise error rate of ~5%. When all possible pairwise comparisons were made with an —test t test (LSD, without consulting the initial F test), 2,860 of the 10,000 experiments included at least one type 1 error (experiment—wise error rate = 28.6%) and the comparison—wise error rate was 5.097%. However, if all possible pairwise comparisons were made with an —level t test only when the initial F test of overall treatment mean equality was significant (FLSD), then the comparison—wise error rate was 1.615%. These results are similar to those reported in Table 3 of Carmer & Swanson:<sup><a href=‘#ref34’>34</a></sup> with 4,000 experiments and 5 treatments, their experiment—wise error rate of the protected LSD test was 4.8% and the comparison error rate was 1.82%; when unprotected —level t tests were used the experiment—wise error was 25.6% and the comparison—wise error rate was 4.99%.
How are these principles affected when treatments are compared, not with —level t tests, but with overlapping standard errors or overlapping (1−) 100% confidence intervals? In the 10,000–experiment Monte Carlo simulation described above, when the initial F test was not consulted, then 82.953% and 99.467% of comparisons had overlapping standard errors and overlapping (1 −)100% confidence intervals, respectively; these values are similar to those reported in Table 1 (and correspond to 17.047% and 0.533% comparison—wise error rates, respectively). Furthermore, the experiment—wise error rate was 100% for both overlapping standard errors and overlapping confidence intervals. If pairwise comparisons among treatments were made only if the initial F test was significant, then 2.529% and 4.713% of comparisons had overlapping standard errors and overlapping (1 –)100% confidence intervals, respectively (corresponding to 97.471% and 95.287% comparison—wise error rates, respectively).
In many applied sciences, most researchers consider it desirable to determine the significance level of their tests of hypotheses, and although it is widely accepted that there is nothing sacrosanct about (say) a 5%—level test, it is still common in many fields to adopt = 0.05 or = 0.10 when drawing conclusions and advancing recommendations. Tables 1 & 2, Figures 2 & 3 shows that basing inferences on overlapping standard errors or confidence intervals around treatment means leaves much to be desired: this practice does not control type I error rates at commonly—accepted levels.
For a CRD with two treatments, using overlapping standard errors to compare treatment means is a decision tool with a type I error rate that ranges from (at best) 16% when variances are homogeneous and sample sizes are large to nearly 32% when variances are extremely heterogeneous. For a CRD with five treatments (and homogeneous variances), comparison—wise type I error rates based on overlapping standard errors (17.05%) were similar to results observed in two—treatment experiments. However, when pairwise comparisons were performed only after a significant F test of overall treatment mean equality, then comparison—wise type I error rates were 97.47%. Clearly, inspection alone of ‘overlapping standard errors’ is not a reliable substitute for a formal —level hypothesis test (cf Cherry35). In contrast, using overlapping 95% confidence intervals to compare treatment means is a much more conservative strategy in two—treatment experiments, with a type I error rate as low as 0.56% when variances are homogeneous to (at most) 5% when variances are extremely heterogeneous. This procedure was similarly conservative in five treatment experiments (with homogeneous variances) when unprotected —level t tests were used. However, if —level t tests are used only following a significant overall F test, then comparison—wise type I error rates based on 95% confidence intervals are high (95.29%).
Similar considerations apply to a paired setting, although there are more factors that affect the probability that standard errors (or confidence intervals) overlap. For example, a negative covariance between treatments reduces the probability of overlap and a positive covariance increases the probability of overlap (relative to the independence case). And increasing variability attributable to the random block effect increases probability of overlap. Thus, in an RBD with t > 2 treatments, where it is likely that the correlation between pairs of treatments will vary (even when sphericity is satisfied), the probability of overlap will vary as the correlation between pairs of treatments varies.
If one wants to compare means in a two—treatment experiment and have an idea of the type I error rate for the comparison, then using overlapping standard errors gives a very liberal idea of that error rate (on average, more differences will be declared than actually exist) and using overlapping confidence intervals gives a very conservative idea of that error rate (i.e., the test will have lower power than the nominal level). Similar conclusions apply to a five—treatment experiment with inferences based on treatment mean comparisons that are not protected by a significant F test on overall treatment mean equality. If, however, treatment mean comparisons are made only following a significant F test in a five—treatment experiment, comparison—wise type I error rates are high (~95%) whether overlapping standard errors are used or overlapping 95% confidence intervals are used. Put another way, neither approach—using overlapping standard errors or using overlapping confidence intervals—gets you where you want to be if the goal is to attach an accurate P—value to an inference, a conclusion reached by Schenker &Gentleman36 as well.
In fact, the only way to compare treatment means with a type I error rate that approximates the nominal level is to formally test with Student’s t test which controls the error rate for all sample sizes as long as assumptions are satisfied. And this formal test is equivalent to estimating a confidence interval around the difference between treatment means—if this interval includes zero, then there is no significant difference between treatments. In fact, the most complete analysis and presentation of results would include
This recommendation in no way discourages the presentation of standard errors and/or confidence intervals around treatment means (e.g., Figure 1b & 1c): this is vital descriptive information which enables an assessment of the precision of our estimates of treatment means. But standard errors (or confidence intervals) around each of two means—and whether they overlap or not—is not a reliable indicator of the statistical significance associated with a test of the hypothesis of mean equality, despite common interpretations to the contrary: for this purpose, interest must shift to a confidence interval around the difference between two means.
One might argue that the last column in Table 1 and the last 3 columns in Table 2 are not necessary. The distribution of the t statistic is known, and so the nominal level is exact: these columns simply reflect simulation variability, and tell us nothing about the behavior of the test statistic that we do not already know. And this is absolutely true. However, a common criticism of—and misunderstanding about—null hypothesis testing is expressed in the following claim: ‘Give me a large enough sample size and I will show you a highly significant difference between two treatments whether a true difference exists or not’ (a claim once made to me by a journal editor). These columns clearly show that this is not correct: type I error rates of the t test were about 5% whether the sample size was n = 5 or n = 1,000: strictly speaking, the type I error rate of a t test of hypothesis is not a function of sample size (nor is it a function of the variance of the random nuisance variable in a paired setting). Statistical power is, of course, affected by sample size; and whereas the two—fold criticism that (1) the ‘null effect’ is likely never precisely zero (but see Berger & Delampady37, who argued that the P—value corresponding to a point null hypothesis is a reasonable response to this criticism), and (2) even a small difference may be significant with a large enough sample size (e.g., Lin et al.38) is well—founded, this is not the issue addressed in this paper. Furthermore, the probability that two standard errors overlap (when the null hypothesis is true) is only a weak function of sample size: this probability was ~0.83—similar to the asymptotic probability of ~0.84—with sample sizes as small as n = 20. Likewise, the probability that two confidence intervals overlap is not (much of) a function of sample size: this probability was very similar to the asymptotic probability with sample sizes throughout the range of n = 5 to n = 1, 000.
The basic thesis of this paper is that using ‘overlap’—either of standard errors or confidence intervals estimated around each treatment mean—is unwise if the goal is to draw an inference about the equality of treatments means at commonly—used significance levels. In the area of multivariate analysis of variance, however39,41, developed an analytical/graphical comparison between treatments that combines the intuitive appeal of an easy—to—understand display of overlap—in this case, between ‘error’ and ‘treatment’ ellipses—with the inferential guarantee of a specified —level test of hypothesis. To appreciate this approach, it is helpful to recall that a confidence interval around a treatment mean is a unidimensional concept: defines a region in a one—dimensional space such that there is a (1−) 100% chance that the interval includes the true population mean. When two (or more) dependent variables are measured, then a confidence ellipse (or ellipsoid) can be formed that defines a region in 2— (or higher—) dimensional space that has a (1− ) 100% chance of encompassing the true population centroid. Friendly and Fox et al.39–41 applied these ideas to ‘error’ and ‘treatment’ ellipses based on the sums of squares and cross—products matrices for the treatment and error effects in a multivariate analysis of variance. In this multivariate analysis, the treatment ellipse (or line) can be scaled so that, if it is included within the boundary of the error ellipse in all dimensions in the space defined by dependent variables (i.e., if the treatment ellipse ‘does not overlap’ the error ellipse), then there is no statistical difference (at the specified level) between the treatments (Figure 4a). If the treatment ellipse extends beyond the boundaries of the error ellipse (i.e., ‘overlaps’ the error ellipse), then centroids differ between treatments in the dimension defined by the linear combination of dependent variables that is represented by the major axis of the ellipse (corresponding to Roy’s Maximum Root criterion with test size ) (Figure 4b).
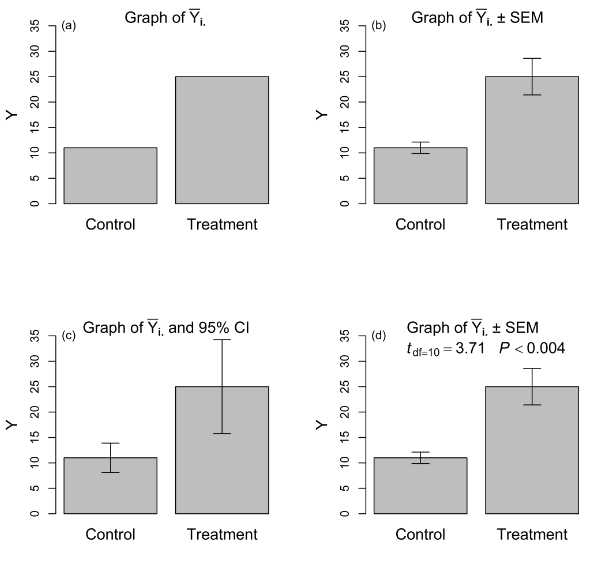
Figure 4 (a) A non-significant (P = 0.07) multivariate F test (Roy’s Maximum Root Criterion) for a case with three treatments and two dependent variables, Y1 and Y2; therefore, the treatment ellipse lies inside the error ellipse, indicating that there is no linear combination of Y1 and Y2 along which treatments are significantly different (univariate tests for both dependent variables are not significant at > 0.10). (b) A significant (P < 0.0001) multivariate F test (Roy’s Maximum Root Criterion); therefore, the treatment ellipse extends outside (i.e., overlaps) the boundaries of the error ellipse in the direction of the linear combination of Y1 and Y2 that maximizes a difference between treatment centroids that is statistically significant (univariate tests for both dependent variables are not significant at P = 0.06). Solid square, round and triangular dots represent treatment centroids; the ‘X’ is the overall centroid.
The proper interpretation of standard error bars and confidence intervals has received attention in the literature (e.g., Goldstein & Healy31; Payton et al.;26 Payton et al.;27 Cummings et al.;42 Cummings & Finch43; Afshartous & Preston32). It is also true, however, that misinterpretation is common, with the possibility of misleading or erroneous inferences about statistical differences. All of the quotations cited in the introduction (above) are from refereed journals in disciplines as diverse as wildlife science, plant ecology, materials science, facial recognition, psychology, and climate science—and so these papers were reviewed by peers as well as associate editors and editors prior to publication. Schenker & Gentleman36 identified over 60 articles in 22 different journals in the medical field which either used or recommended the method of overlap to evaluate inferential significance. Clearly, this approach is widespread and many applied scientists believe the practice is sound. The results in this paper indicate otherwise. And whereas there are many reasons why this practice should be avoided, there is one reason that stands out: when an author declares ‘To more generally compare differences [among treatments], we define non—overlapping standard error values as representative of significantly different [survival estimates]’,44 the effect of such arbitrary redefinition will surely lead to confusion: what one investigator has defined as ‘significant’ will mean something very different from the precisely—defined and widely—accepted meaning of statistical significance, sensu stricto, that has been utilized for decades. To cite two examples, when a climate scientist declares a significant increase in global average temperature over a time period, or a medical scientist declares a significant decrease in cancer tumor size in response to experimental treatment, it is obvious that these claims should be based on the uniformly—accepted definition of what the term ‘significant’ means in a statistical sense.
Statisticians are well aware of the issues raised in this paper, and introductory texts and courses in applied statistics cover this topic. Nevertheless, as the selected quotations in the introduction, above, indicate, misinterpretation of overlapping standard errors and/or confidence intervals has been, and continues to be, common in a variety of applied disciplines, confirming Johnson’s45 observation that ‘. . . men more frequently require to be reminded than informed.’ This should provide renewed motivation
Constructive comments by L.A. Brennan, F.C. Bryant, R.D. DeYoung, E.B. Fish, M.L. Friendly, J.L. Grace, J.P. Leonard, H.G. Mansouri and S. Rideout—Hanzak substantially improved this paper. This is manuscript number 16—101 of the Caesar Kleberg Wildlife Research Institute, Texas A&M University—Kingsville, TX. This work was supported by the Caesar Kleberg Wildlife Research Institute, Texas A&M University—Kingsville, Kingsville, TX, USA.
Author declares no Conflict of interest.

©2018 Wester. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.
2 7