
Research Article Volume 2 Issue 2
Combinational effects of clinical area and healthcare workers’ job type on the safety culture in hospitals
Heon Jae Jeong,1 
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Su Mi Jung,2 Eun Ae An,3 So Yeon Kim,4 Byung Joo Song4
1Department of Health Policy and Management, Johns Hopkins Bloomberg School of Public Health, Johns Hopkins University, USA
2Data Analytics center, Kangwon National University, Korea
3Leadership Development Division, The Catholic Education Foundation, Korea
4Performance Improvement Team, Seoul St. Mary?s Hospital, The Catholic University of Korea, Korea
Correspondence: Heon-Jae Jeong, Department of Health Policy and Management, Johns Hopkins Bloomberg School of Public Health, Johns Hopkins University, 624 North Broadway, Rm. 455, Baltimore, MD, 21205, USA, Tel 410-955-5315, Fax 410-955-6959
Received: March 04, 2015 | Published: March 17, 2015
Citation: Jeong HJ, Jung SM, An EA, et al. Combinational effects of clinical area and healthcare workers’ job type on the safety culture in hospitals. Biom Biostat Int J. 2015;2(2):45-51. DOI: 10.15406/bbij.2015.02.00024
Download PDF
Abstract
As patient safety is taking center stage in medical care, many resources have been invested to improve safety. Patient safety culture has been one of the most important constituents of safety and, therefore, has been measured with various instruments. One fundamental challenge is that a healthcare worker’s safety attitude can be shaped by multiple factors such as job type and clinical area. Due to the complex organizational and cultural structure in a hospital, such multi-dimensional dynamics are not thoroughly understood. This study used the crossed random effects model to assess combinational effects of clinical area and job type and calculate the safety attitudes score of each combination with the empirical Bayes (EB) method. We used the Korean version of the Safety Attitudes Questionnaire (SAQ-K), which consists of six domains: teamwork climate (TC), safety culture (SC), job satisfaction (JS), stress recognition (SR), perception of management (PM) and working conditions (WC). Each clinical area and job type independently affects SAQ-K scores of all six domains. For TC, SC, SR, and PM, there were combinational effects of clinical area and job type on SAQ-K scores (e.g., a certain job type in a certain clinical area showed higher or lower SAQ-K scores than another clinical area, or the other way around). We also applied the EB method to achieve more accurate combination-level estimates when the variance in SAQ-K score of the combination was large, which is a common situation in hospitals with multiple clinical areas and job types.
Keywords: safety culture, safety attitudes questionnaire, patient safety, variance components model, crossed random effects model, random effect, empirical bayes method
Abbreviations
SAQ, safety attitudes questionnaire; TC, teamwork climate; SC, safety climate; JS, job satisfaction; SR, stress recognition; PM, perception of management; WC, working conditions; EB, empirical bayes; LR, likelihood-ratio; HCWs, healthcare workers
Introduction
This article is the second in a series of articles on methodology to analyze patient safety culture among healthcare workers (HCWs). In the previous article, we developed and validated the Korean version of the Safety Attitude Questionnaire (SAQ-K) and proposed a method to estimate SAQ-K scores for clinical area more accurately than traditional SAQ analysis methods.1 Here, we expand the scope to devise methods to explore combinational effects of different characteristics, clinical area and job type.
In any industry with the risk of accidents, safety culture and climate among the workers are considered the most important drivers for safety improvement initiatives; this environment provides momentum for workers to adhere to the safety rules and better collaborate to build a highly reliable organization.2-5 Health care is no exception and many resources have been invested to improve and manage safety culture. The first and foremost step was to measure the culture, and thus various instruments were developed to do so.6-8 Among those instruments, the Safety Attitudes Questionnaire (SAQ) is one of the most popular and thoroughly validated instruments, consisting of six distinct domains: teamwork climate (TC), safety climate (SC), job satisfaction (JS), stress recognition (SR), perception of management (PM), and working conditions (WC).9 Since it was developed, SAQ has been translated into various languages and used in many countries;10-15 recently, the SAQ-K was developed to enable international comparison of safety profiles between Korea and other countries.1
To date, the SAQ has been used mostly to show clinical area-specific scores and compare them across hospital (cross-sectional) or temporal changes.16 Though less frequently used, job type-specific scores have also been of interest in a few studies.14 Both approaches are meaningful in that clinical area naturally determines the culture in which an HCW is submerged, and job type also can influence safety attitudes since it reflects how one was trained and of what professional society one is a member, which can influence the power gradient across different job types.17 However, few studies have explored the effects of those two factors simultaneously, especially their interaction in influencing safety culture. The difficulties arise because most healthcare organizations have multiple, sometimes tens of, clinical areas and various job types. Traditional models cannot address the complexity between clinical area and job type, which might easily exceed hundreds of combinations. In addition, huge variation exists in the number of HCWs in each combination, which makes the dataset highly unbalanced, frequently with unequal variances. Indeed, many combinations have only one or two HCWs and, thus, para meterizing the effects of all these combinations is neither practical nor efficient.
Therefore, we applied the crossed random effects model with an interaction term between clinical area and job type. With this model, we can effectively control the issues of too many combinations, as well as the problem from a heavily unbalanced data structure.18-21
Another advantage of using the random effects model is that it allows for applying the empirical Bayes (EB) method to obtain more accurate estimates of SAQ scores from each clinical area and job type combination.1 The EB method operates by letting areas and job types with large variance that is typically caused by small sample size borrow information from areas and job types with small variance.21-24 The theoretical background of Bayes method is to use prior distribution as a starting point, and update the distribution with the actual observations. For example, if we want to obtain a Bayesian estimate of one domain score of SAQ-K in a certain cluster (e.g., clinical area and job type), we first assume a prior distribution of the cluster level random effect across the hospital, and apply the specific information from the cluster to the prior distribution. Thus, Bayesian estimates are natural compromise between prior distribution over clusters and cluster-specific scores, and larger the variance of a cluster-specific score, the more weight is assigned to the prior distribution. Therefore, choosing an appropriate distribution is probably one of the most important steps for the Bayesian estimation process, requiring much experience from a researcher.25 On the other hand, EB method does not force one to set a prior distribution; rather, it utilizes data of interest to generate prior distribution of the cluster random effect first, and pretends that data has not been used yet.21 With prior distribution obtained, the same steps described above can be used to obtain more accurate cluster-specific estimates. This is why this method is called the empirical Bayes. In this particular study, EB not only provided accurate estimates, but also served as a convenient tool to estimate the SAQ score of each combination.1
Therefore, this study was conducted with three goals:
- Test whether SAQ scores vary significantly over clinical area and job type,
- If so, test whether there is a combinational effect of clinical area and job type on SAQ scores, and
- Apply the EB method to obtain the SAQ score of each combination.
Methods
Because this study shares the dataset from the previous SAQ-K series article,1 the detailed process of survey development and validation is not described in this article. However, information regarding survey respondents and basic data structure is essential to describe this study, and therefore they are depicted in the first parts of the methods and results sections.
Administering the Korean version of safety attitude questionnaire
To measure safety culture by clinical area and job type, we utilized the Korean version of the Safety Attitude Questionnaire. The SAQ-K was developed and validated with permission of the original SAQ developers and composed of 34 items in 6 domains -TC (5 items), SC (6 items), JS (5 items), SR (4 items), PM (10 items), and WC (4 items)- and demographic information, including the respondent’s clinical area and job type.
The SAQ-K was administered anonymously to healthcare workers in a large metropolitan hospital in Seoul from October 2013 through November 2013. Two options of modality were offered for respondents’ convenience in administering the SAQ-K: paper and pencil survey and electronic survey via the hospital’s intranet.
A 5-point Like rt scale (1 = Disagree Strongly, 2 = Disagree Slightly, 3 = Neutral, 4 = Agree Slightly, 5 = Agree Strongly) was used to measure SAQ-K items and the scores were then converted into 0 to 100 scales as the original SAQ developers recommended. Domain scores were obtained for each respondent by calculating the arithmetic mean score of each domain.
Individual effect of clinical area and job type on SAQ scores
The following model-building steps are applied to each of the six SAQ-K domains because differences across domain scores are outside the scope of this study. In this section, we explored whether each of the clinical area and job type variables explains the variance of SAQ-K scores with statistical significance. First, we began with a simplest model for a domain score,
of person
.
is the overall hospital mean of the SAQ-K scores of all survey participants.
is the random deviation of the SAQ-K score of a person
from the overall mean
.
Here,
is assumed to follow a normal distribution with a mean of 0 and variance
. Then we developed a variance components model by adding clinical area effects and obtained the following model to describe the SAQ-K score,
of person
, working in clinical area
,
where
is the overall mean of SAQ scores for a certain domain and
is a random deviation of the mean SAQ score for clinical area
from
. The random effect of clinical areas
is assumed to be normally distributed, having a mean of 0 and variance
, and to be independent over clinical areas. Therefore,
is the random deviation of
from the mean of clinical area
, that is, the residual within the clinical area.
is also assumed to follow a normal distribution with a mean of 0 and variance
and be independent of both clinical areas and survey respondents.
21
We then developed another variance components model with job type
as the random effect instead of clinical area
,
where all the variables and their assumptions are equivalent to those of model 1.2, except that they address job type rather than clinical area. To be specific,
, the main variable of interest; random deviation of the mean SAQ scores of job type
from
is assumed to follow a normal distribution with 0 mean and
variance.
At this point, we tested whether clinical area and job type significantly influence the SAQ domain scores. For clinical area, the likelihood-ratio (LR) test was conducted to test the null hypothesis, H0:
= 0, by comparing model 1.2 to model 1.1. For job type, the null hypothesis, H0:
= 0, with the LR test, was used to compare model 1.3 to model 1.1. Since
and
cannot have negative values, the p-values obtained from the LR tests had to be divided by 2.21 All p-values in this article are those that were derived earlier.
Combinational effects of clinical area and job type on SAQ scores
We built a crossed random effects model for each SAQ domain. First, we developed a model that includes both clinical area random effect and job type random effect. In this model, neither clinical area nor job type is nested in the other. In other words, we did not assume any hierarchy between clinical area and job type, and thus the following model is an additive crossed random effects model:
where
is the SAQ domain score of a person
, whose job type was
, working in clinical area
. Again,
is the overall mean of the SAQ domain score of all respondents, and
and
are the random deviation of the mean SAQ scores of clinical area
and job type
around
, respectively. As in models 1.2 and 1.3,
and
are assumed to follow normal distributions with a mean of 0 and variance of
and
, respectively. Therefore,
is the random deviation of
from the sum of
,
and
, and is assumed to be normally distributed with a mean of 0 and variance
. Here,
reflects not only the variability among HCWs with a certain job type working in the same clinical area, but also interactions between clinical area and job type, that is, deviations of the mean SAQ scores for the combinations of clinical area and job type from the means that are implied in the additive manner of the random effects.
21
Then, we added the random interaction term
. Here, the interaction means that the SAQ scores of clinical area and job type are correlated; for example, nurses in a cardiac intensive care unit responded more positively to SAQ than nurses in other clinical areas. The rationale of having this variable was that several combinations of clinical area and job type included multiple HCWs. Since
can have different values for different combinations of clinical area
and job type
, this model actually relaxed the additive assumption of model 2.1 and allowed us to quantify the combinational effects:21
where all the variables and their assumptions are the same as in model 2.1. The random interaction term,
follows normal distribution with a 0 mean and variance,
.
is assumed to be independent of the other random terms,
, and
over combinations of clinical area and job type.
21
Through an LR test comparing model 2.2 to model 2.1, we can test the null hypothesis H0:
= 0. If the LR test rejects the null hypothesis, then there were combinational effects of clinical area and job type on SAQ scores. If not, plugging in the interaction term does not add any value, and therefore we would just return to model 2.1. The p-values of the LR test results in this article were adjusted to test on the boundary of parameter space, as indicated in an earlier section.21
Combination-specific empirical bayes estimation of SAQ scores
From model 2.2, we used the EB method to achieve the estimations of random effects,
,
and
for each combination and, by summing them, we obtained combination-specific random deviation from the overall mean SAQ domain score. If the interaction term was not statistically significant, we returned to model 2.1 and used only
and
to obtain the deviation. By adding the overall mean,
, to the random deviation, we obtained the SAQ score of each combination.
For all the analyses, Stata 13.1 (Stata Corp, College Station, Texas) was used.
Result
Characteristics of respondents
A total of 1,381 questionnaires was returned. After excluding those missing clinical area and job type variables, 1,142 questionnaires were analyzed. As depicted in Table 1, 73.7% of the survey respondents was female. Regarding work experience, HCWs with 5-10 years of experience formed the largest portion (25.4%) of the respondents, followed by HCWs with 3-4 years of experience (21.8%). There were 16 job types among the respondents. Nurses were 53.3% and physicians were the next largest group. Among physicians, residents accounted for 14.5%, followed by senior physicians (9.9%), clinical instructors (5.6%), and interns (3.1%). Additional personnel included radiology technologists (4.5%), medical laboratory technologists (1.8%), and clinical supporting staff (3.5%). Since almost all nurses in Korea are female, nurses comprised more than half of the respondents.
Characteristics |
N |
% |
Gender |
|
|
Male |
300 |
26.3 |
Female |
842 |
73.7 |
Work years |
|
|
Less than 6 months |
77 |
6.7 |
7 ~ 11 months |
122 |
10.7 |
1 ~ 2years |
193 |
16.9 |
3 ~ 4 years |
249 |
21.8 |
5 ~ 10 years |
290 |
25.4 |
11 ~ 20 years |
150 |
13.1 |
Over 21 years |
61 |
5.3 |
Job type |
|
|
Nurses |
609 |
53.3 |
Residents |
166 |
14.5 |
Senior physicians |
113 |
9.9 |
Clinical instructors |
64 |
5.6 |
Radiologic technologists |
51 |
4.5 |
Clinical supporting staff |
40 |
3.5 |
Interns |
35 |
3.1 |
Medical laboratory technologists |
20 |
1.8 |
Pharmacists |
10 |
0.9 |
Dental hygienists |
10 |
0.9 |
Physical therapists |
6 |
0.5 |
Administration |
5 |
0.4 |
Hospital officers |
4 |
0.4 |
Other |
4 |
0.4 |
Nutritionists |
3 |
0.3 |
Medical record officers |
2 |
0.2 |
Total |
1142 |
100.0 |
Table 1 Characteristics of respondents
Although not reflected in Table 1, the hospital had 72 clinical areas. To briefly introduce the dispersion of HCWs by clinical area, we summarized the data in stem-and-leaf plots, as seen in Figure 1. The numbers of HCWs varied substantially over the 72 clinical areas, ranging from 2 to 53 HCWs. We do not show specific names of clinical areas because they were not of interest in this study

Figure 1 Stem-and-leaf plots of the number of respondents by clinical area.
Table 2 depicts the combinations of clinical area and job type. To illustrate, 12 clinical areas had only one job type working, 12 clinical areas had two different job types, and 19 clinical areas had three job types working. Two areas had nine job types, which was the largest number of job types in one unit. There were 243 different combinations between clinical area and job type. Although not shown in Table 2, the largest combination had 34 HCWs.
Number of job types
in a clinical area (a) |
Number of
clinical areas (b) |
Number of clinical area and
job type combinations (a x b) |
1 |
12 |
12 |
2 |
12 |
24 |
3 |
19 |
57 |
4 |
14 |
56 |
5 |
5 |
25 |
6 |
6 |
36 |
7 |
1 |
7 |
8 |
1 |
8 |
9 |
2 |
18 |
Total |
72 |
243 |
Table 2 Number of clinical area and job type combinations
Internal Consistency and Construct Validity
We calculated Cronbach’s alpha to check internal consistency, which was 0.836 for TC, 0.841 for SC, 0.907 for JS, 0.734 for SR, 0.928 for PM, and 0.758 for WC. The results of confirmatory factor analysis suggested good model fit:26 goodness of fit index (0.911), adjusted goodness of fit index (0.894), normed fit index (0.924), comparative fit index (0.944), and root mean square error of approximation (0.044).
Effects of Clinical Area and Job Type on SAQ-K Domain Scores
Table 3 contains the results from the first three models. For model 1.1, the naked model without random effects, the overall means (
) and standard deviations (
) of the six SAQ-K domain scores are listed. For model 1.2, the overall means (
), standard deviations (
) of the clinical area random effect around the overall mean, and standard deviation (
) of residuals around clinical area-specific mean for six SAQ-K domains are listed. Model 1.3 has the same structure as model 1.2, except for having a standard deviation (
) of job type, instead of clinical area, random effects. LR test results are also described as superscripts beside random effects standard deviations.
The means (
s) of the three models were similar, ranging from 55.23 (WC in model 1.1) to 68.84 (SR in model 1.2). Note that the mean of JS was much different between the model with job type random effect (65.15 in model 1.3) and the other two models (58.55 in model 1.1 and 59.52 in model 1.2). For both model 1.2 and 1.3, all the random effects for the six domains were statistically significant from LR tests. JS showed the largest standard deviation of clinical area random effects,
, at 7.84, and SR showed the smallest
at 3.29. The standard deviation of job type random effects,
, was the largest in JS (6.54) and the smallest in PM (1.54).
|
TC |
SC |
JS |
SR |
PM |
WC |
Model 1.1 |
|
64.86 |
65.32 |
58.55 |
68.66 |
61.39 |
55.23 |
|
17.60 |
16.47 |
21.26 |
18.51 |
17.23 |
16.70 |
Model 1.2 |
|
65.60 |
65.65 |
59.52 |
68.84 |
61.78 |
55.65 |
|
|
5.35* |
3.74* |
7.84* |
3.29* |
3.79* |
3.88* |
|
16.85 |
16.03 |
20.00 |
18.19 |
16.78 |
16.27 |
Model 1.3 |
|
66.99 |
66.20 |
65.15 |
65.22 |
61.20 |
56.10 |
|
3.23* |
2.88* |
6.54* |
4.10* |
1.54* |
1.95* |
|
17.31 |
16.33 |
20.27 |
18.10 |
17.16 |
16.60 |
Table 3 ASAQ-K domain scores and variance components model parameters
* : p<0.05 from the LR tests comparing the model to model 1.1
Table 4 describes parameters from the crossed random effects models. The means (
s) of the two models were similar. The main interest of these crossed models was the standard deviation (
) of the random interaction term in model 2.2. For the TC, SC, SR, and PM domains, the random interactions were statistically significant, suggesting that certain clinical areas were related to the SAQ domain scores of certain job types, or the other way around. The JS and WC domains showed the smallest standard deviations (
) of the random interaction term (JS: 2.95 and WC: 2.42) and these were not statistically significant.
|
TC |
SC |
JS |
SR |
PM |
WC |
Model 2.1 |
|
67.59 |
66.50 |
64.72 |
65.43 |
61.46 |
56.23 |
|
3.47 |
3.97 |
5.20 |
2.86 |
3.97 |
3.57 |
|
4.73 |
3.50 |
6.15 |
4.06 |
1.88 |
1.66 |
|
16.67 |
15.83 |
19.70 |
17.87 |
16.68 |
16.25 |
Model 2.2 |
|
67.62 |
66.37 |
64.84 |
65.39 |
61.50 |
56.24 |
|
3.64 |
2.63 |
4.60 |
1.07 |
3.16 |
3.20 |
|
3.41 |
2.86 |
6.21 |
3.94 |
1.59 |
1.69 |
|
4.96* |
4.50* |
2.95 |
5.52* |
3.79* |
2.42 |
|
16.30 |
15.54 |
19.61 |
17.37 |
16.46 |
16.46 |
Table 4 Crossed random effects model parameters
* : p<0.05 from the LR tests comparing model 2.2 to model 2.1
Empirical Bayes Estimation of Combination-Specific SAQ-K Scores
To obtain estimates of SAQ-K scores specific to clinical area and job type combinations, we used the empirical Bayes method. For the TC, SC, SR, and PM domains, model 2.2 was used since the random interaction term significantly affected SAQ-K scores. For the JS and WC domains where interaction was not significant in LR tests, we returned to model 2.1. Since showing specific names of clinical area and job type was not the purpose of this study, we depicted the combination-specific SAQ domain scores without identifying clinical area or job type in Figure 2. The y-axis on the left side is the SAQ-K domain score and the right side is the deviation of the combination-specific SAQ-K score from the domain means score.
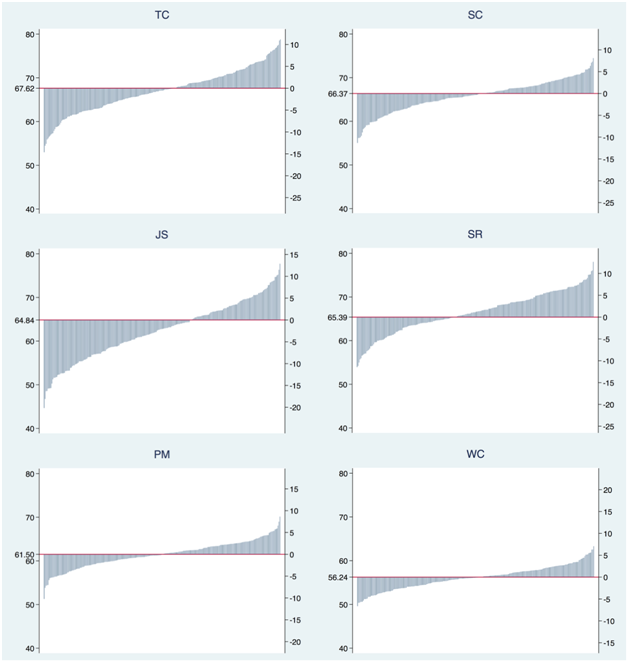
Figure 2 Combination-specific SAQ-K score (EB) and its deviation from the mean for all six SAQ-K domains.
Note: x axis: combination of clinical area and job type; y axis (left): SAQ-K domain score; y axis (right): deviation of SAQ-K score from mean.
Discussion
The primary aim of this study was to examine whether effects in SAQ-K scores arise from different combinations of clinical area and job type. To pursue this aim, we applied a crossed random effects model, known as the two-way error components model, with a random interaction term and tested whether the interaction existed for each of the six SAQ-K domains.
One might wonder why we did not use ordinary least squares (OLS) regressions or the fixed effects (FE) model on existing combinations of clinical area and job type-this particular study had 243 combinations-rather than applying random effects. Actually, OLS and FE models are computationally simple, and they might provide more intuitive combination-specific scores. However, those models cannot statistically prove or disprove whether clinical area and job type affect the SAQ-K scores in conjunction. That is, we had to parameterize the dispersion of SAQ-K scores over clinical area and job type, and then we could decide whether there was an interaction between them.
In model 2.1, we had two random effects, clinical area and job type, with the assumption that they were not correlated; that is why we call it an additive model. This was a strong assumption, and anyone who has experience in HCWs’ working environment might say the assumption cannot hold. Actually, that was the strategy of this study: If there is correlation between them, the estimators of their random effects might be incorrect, and the correlation is reflected in the residuals of the model. Then we added the interaction term that will take up the correlation absorbed in the residual. If there was significant interaction, the latter model yielded better likelihood. If there was no significant interaction, then we discarded the interaction term and returned to the additive model.
Also, as a byproduct of this random effects approach, we could easily calculate EB estimates of SAQ scores for each of the 243 clinical area-job type combinations. The EB predictor is the best linear unbiased predictor (BLUP) and is particularly useful in the hospital of this study where the SAQ-K was administered. A total of 1,142 HCWs responded to the survey, which means that each combination had only around 4.7 HWCs on average. Considering the largest combination had 34 HCWs, many combinations contained fewer than 4.7 HWCs, even 1 or 2. For those small combinations, simple calculation of the combination-specific mean does not provide much information, especially for those who determine resource allocation for safety improvement programs in a hospital. EB methods can improve the accuracy of combination-specific estimates by allowing small combinations to borrow strengths from other combinations that have larger sample size and small standard deviation.21,23,24,27
Other model structures could have multiple random effects variables, such as clinical area job type. For example, we could build a three-level hierarchical model where job type is nested under clinical area, or the other way around. Though we explored those models, we returned to the current crossed random effects model. Clinical area is most obviously the key clustering variable regarding safety culture1 since HCWs in one area work together and communicate every day. Job type plays a role in shaping culture as much as physical work area; there are many training and education programs and sessions for specific job types, letting them share similar attitudes on safety. In this case, structuring clinical area and job type in a matrix format would be a more reasonable approach and modeling such matrix as a statistical equation is the crossed random effects model.
With regard to data structure, note that 609 nurses comprised more than half of the survey respondents. Unlike physician groups, such as residents and interns, which were measured with higher resolution, all 609 nurses were measured as one group. This was because there were only a few nurses at a higher position and almost all the nurses perform the same work. Though their actual roles might vary and this could affect their SAQ-K scores, such difference can be captured in the clinical area variable or the interaction term, which is the rationale of this study. With respect to analysis, the only concern arising from a huge nurses group is that the number of clusters could be small, which could lead to difficulty in assigning value to the random parameter. However, in this particular study, 16 different job types existed and, therefore, no significant problem arose in plugging in the job type as a random effect.21
The overall means from all models were similar for all domains, with the exception of the JS domain. In model 1.1, the simplest model without random effects, and model 1.2, the model with clinical area as the random effect, the mean was 58.55 and 59.52, respectively. However, the rest of the models, all of which contain job type as random effects, the means were around 65. This is because the overall mean is estimated inversely proportional to cluster variances in the random effects model. If a small cluster has small within-cluster variance compared to between-cluster variance, then the cluster can have a weight similar to the large cluster. Thus, compared to the ordinary least squares model, the random effects model is likely to put more weight on small clusters.21 In this study, job type might have caused such effect in the JS domain. Though this phenomenon is not the focus of this study, it is worthy of examination in a future study, especially regarding SAQ score differences across domains.
We used the LR test as the primary method to test the significance of random effects for each model. Basically, the LR test compares one model to another, and it is especially efficient when a model is built on top of another, which is the case of this study. However, note that several inferential methods can be applied other than the LR test, such as pseudo quasi-likelihood, also known as joint maximization methods.28,29 Especially when multiple covariates are added, step-by-step comparison with LR would not be efficient. Future studies including various respondent characteristics and area-specific or job type-specific information should take advantage of such other inferential strategies.
Although we built crossed random effects models by carefully addressing both mathematical challenges and real-world situations, there were some issues that the structure of data in this study could not clearly handle. First and foremost, it is difficult to establish whether an HCW is working in more than one clinical area. To illustrate, if a surgeon is working in both an operating room and a surgical intensive care unit, to which clinical area should his or her responses be assigned? To date, we have forced these respondents to choose one clinical area and regarded that respondent as working in a single clinical area, even thought is not true. The methodology used in this study can be applied to resolve the issue by asking respondents to identify their primary clinical area and their secondary clinical area. Then we can apply the crossed random effects model with those two areas exactly as we did with one clinical area and one job type. In that situation, the surgeon’s response can be thought of as shaped by the safety attitudes of both the operating room and the intensive care unit. With this approach, we can develop a much more detailed map that shows the topography of safety culture.
Conclusion
Following up the previous SAQ-K article that investigated the effects of clinical areas on SAQ-K score distribution,1 we examined how job type influenced the SAQ-K in this study. We showed that not only did clinical area and job type affect SAQ-K scores independently, but they also interact and affect HCWs’ safety attitudes. In addition to the results of this study, the methodology that we devised can help healthcare organizations better understand their safety culture, on which they can develop more effective patient safety improvement programs. We hope this study assists in hospitals’ relentless endeavor to save lives.
Acknowledgement
Conflict of interest
References
- Heon-Jae Jeong, Su Mi Jung, Eun Ae An, et al. Development of the Safety Attitudes Questionnaire - Korean Version (SAQ-K) and Its Novel Analysis Methods for Safety Managers. Biom Biostat Int. 2015;2(1):00020.
- Zhang H, Wiegmann DA, Von Thaden TL, et al. Safety Culture: A Concept in Chaos? Proceedings of the Human Factors and Ergonomics Society Annual Meeting. 2002;46(15):1404‒1408.
- Chassin MR, Loeb JM. High‐Reliability Health Care: Getting There from Here. Milbank Q. 2013;91(3):459‒490.
- Von Thaden TL, Wiegmann DA, Mitchell AA, et al. Safety culture in a regional airline: Results from a commercial aviation safety survey. Paper presented at 12th International Symposium on Aviation Psychology: Dayton, OH; 2003.
- Reason J. Safety paradoxes and safety culture. Injury Control and Safety Promotion. 2000;7(1):3‒14.
- Morello RT, Lowthian JA, Barker AL, et al. Strategies for improving patient safety culture in hospitals: a systematic review. BMJ Qual Saf. 2013;22(1):11‒18.
- Etchegaray JM, Thomas EJ. Comparing two safety culture surveys: safety attitudes questionnaire and hospital survey on patient safety. BMJ Qual Saf. 2012;21(6):490‒498.
- Colla J, Bracken A, Kinney L, et al. Measuring patient safety climate: a review of surveys. Qual Saf Health Care. 2005;14(5):364‒366.
- Sexton J, Helmreich R, Neilands T, et al. The Safety Attitudes Questionnaire: psychometric properties, benchmarking data, and emerging research. BMC Health Serv Res. 2006;6(1):44.
- De Carvalho RE, Cassiani SH. Cross-cultural adaptation of the Safety Attitudes Questionnaire-Short Form 2006 for Brazil. Rev Lat Am Enfermagem. 2012;20(3):575‒582.
- Zimmermann N, Kung K, Sereika SM, et al. Assessing the safety attitudes questionnaire (SAQ), German language version in Swiss university hospitals-a validation study. BMC Health Serv Res. 2013;13(1):347.
- Norden-Hagg A, Sexton JB, Kalvemark-Sporrong S, et al. Assessing Safety Culture in Pharmacies: The psychometric validation of the Safety Attitudes Questionnaire (SAQ) in a national sample of community pharmacies in Sweden. BMC Clin Pharmacol. 2010;10(1):8.
- Deilkas ET, Hofoss D. Psychometric properties of the Norwegian version of the Safety Attitudes Questionnaire (SAQ), generic version (short form 2006). BMC Health Serv Res. 2008;8(1):191.
- Lee WC, Wung HY, Liao HH, et al. Hospital safety culture in Taiwan: a nationwide survey using Chinese version safety attitude questionnaire. BMC Health Serv Res. 2010;10(1):234.
- Raftopoulos V, Pavlakis A. Safety climate in 5 intensive care units: A nationwide hospital survey using the Greek-Cypriot version of the Safety Attitudes Questionnaire. J Crit Care. 2013;28(1):51‒61.
- Watts BV, Percarpio K, West P, et al. Use of the safety attitudes questionnaire as a measure in patient safety improvement. J Patient Saf. 2010;6(4):206‒209.
- Jeong H-J, Pham JC, Kim M, et al. Major cultural-compatibility complex: considerations on cross-cultural dissemination of patient safety programmes. BMJ Qual Saf. 2012;21(7):612‒615.
- Raudenbush SW. A crossed random effects model for unbalanced data with applications in cross-sectional and longitudinal research. Journal of Educational Statistics. 1993;18(4):321‒349.
- Baayen RH, Davidson DJ, Bates DM. Mixed-effects modeling with crossed random effects for subjects and items. Journal of memory and language. 2008;59(4):390‒412.
- McCulloch CE, Neuhaus JM. Generalized linear mixed models. Wiley Online Library; 2001.
- Rabe-Hesketh S, Skrondal A. Multilevel and Longitudinal Modeling Using Stata. 2nd ed. College Station, Stata Press: Texas, USA; 2008.
- Militino A, Ugarte M, Goicoa T. A BLUP synthetic versus an EBLUP estimator: an empirical study of a small area estimation problem. Journal of Applied Statistics. 2007;34(2):153‒165.
- Berger J. Parametric Empirical Bayes Inference: Theory and Applications: Comment. Journal of the American Statistical Association. 1983;78(381):55‒57.
- Carlin BP, Louis TA. Bayes and empirical Bayes methods for data analysis. Statistics and Computing. 1997;7(2):153‒154.
- Lynch SM. Introduction to applied Bayesian statistics and estimation for social scientists. Springer Science & Business Media; 2007.
- Hair JF, Tatham RL, Anderson RE, et al. Multivariate data analysis. 6th ed. Pearson Prentice Hall Upper Saddle River: New Jersey, USA; 2006.
- Morris CN. Parametric empirical Bayes inference: theory and applications. Journal of the American Statistical Association. 1983;78(381):47‒55.
- Breslow NE, Clayton DG. Approximate inference in generalized linear mixed models. Journal of the American Statistical Association. 1993;88(421):9‒25.
- Bellio R, Varin C. A pairwise likelihood approach to generalized linear models with crossed random effects. Statistical Modelling. 2005;5(3):217‒227.

©2015 Jeong, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


