Clinical trial laboratory data nested with in subject: components of variance, sample size and cost

doi:10.15406/bbij.2015.02.00029

eISSN: 2378-315X

Biometrics & Biostatistics International Journal

Conceptual Paper Volume 2 Issue 3

Clinical trial laboratory data nested with in subject: components of variance, sample size and cost

Borko D Jovanovic,¹ Hariharan Subramanian,² Irene B Helenowski,¹ Hemant K Roy,¹ Vadim Backman²

¹Northwestern University, Feinberg School of Medicine, USA
²Boston University, USA

Correspondence: Borko D Jovanovic, Feinberg School of Medicine, Northwestern University Department of Preventive Medicine, 680 N. Lake Shore Drive, Suite 1400, Chicago, IL 60611, USA

Received: March 06, 2015 | Published: April 15, 2015

Citation: Jovanovic BD, Subramanian H, Helenowski IB, et al. Clinical trial laboratory data nested with in subject: components of variance, sample size and cost. Biom Biostat Int J. 2015;2(3):81-83. DOI: 10.15406/bbij.2015.02.00029

Download PDF

Abstract

Nesting of experimental factors is well established in statistical design literature related to agricultural, environmental and engineering studies. It is perhaps not sufficiently discussed in biological and laboratory experiments stemming from the use of human bio-specimens, where sample size considerations are often provided a priori on subject level, but there is little advice regarding the needed number of units at lower levels. Motivated by an example from spectroscopic microscopy and lung cancer, we revisit the experimental nesting frame work and discuss how variability, cost of sampling and sample size at lower levels may be coherently utilized. We show how the number of subjects may have to be adjusted to account for inadequate sampling decisions made at lower levels.

Keywords: clinical trials, sample size, lung cancer, spectroscopic microscopy, ANOVA

Introduction

In randomized clinical trials, the sample size (i.e. the number of subjects planned to be used) is carefully scrutinized, studied in statistics courses, and advised in this realm.¹ Quite contrary to that, the number of sampling units to be studied on sub-subject level is often ignored or chosen according to existing laboratory folklore: e.g. “we always do three repeats”. Most often only the subject and group level data are reported and considered in sample size calculations. The expected effect size is typically considered on a treatment group level as a result of an average or summary across all existing levels: sub-cell level, cell level, tissues level, per human subject, and per treatment group. Sample size calculations are then based on overall measure of variability considering the putative effect size that would make a clinically important difference. Possible knowledge of variability at lower nested levels may be available, but is rarely included in the planning of a trial. This makes the answer to the question ‘how many items should be measured at lower levels, left to budgetary limitations. In this paper, we revisit the nesting framework and discuss how effect size and sample size at various levels may be used in sample size calculations.

Motivating example: A lung cancer study

An observational study Roy et al.² was used as a template for in preparation for designing a randomized clinical trial example. Particularly, it involved collecting Ld measurements of “disorder strength of cell nano architecture” in saliva swab samples, based on partial wave spectroscopic microscopy. The population comprised of lung cancer patients, and three groups of controls: patients with COPD, smoking controls, and nonsmoking controls. Large values of Ld are in theory associated with disarray in cell nano architecture and suggest presence of cell stress, potentially leading to development of cancer.

In the initial study measurements were recorded for each of 135 subjects (cancer, COPD, smokers, non-smokers), with approximately 20-30 cells per subject, and within each cell, data were obtained from approximately 100,000-200,000 pixels per cell, each providing a measure of Ld. Such large number of pixels was provided by a machine which visually recorded the entire cell structure, as a part of a separate project. A summary of results is provided in Figure 1 below. Cancer patients have the largest average level of Ld, followed by COPD patients, smoker-controls, and finally by non-smoking controls. The ROC curves were formed and AUC (ROC) was observed to be in the 0.85 realm.

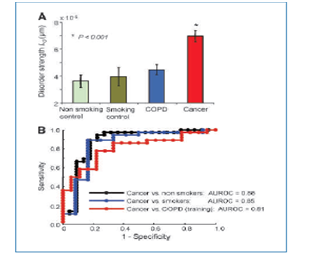
Figure 1 Summary of Roy et al.² study results.

Importantly, measurements were structured such that pixels were nested within cells; cells were nested within subjects, while subjects were nested in several diagnosis groups as in Figure 1. The underlying working hypothesis was that Ld levels sufficiently differ among cancer and control groups so that a prediction rule may be developed and tested prospectively to detect yet undetected cancer cases. Alternatively a prophylactic prevention treatment could be applied to subjects at risk, subjects with high Ld, so that such measure of cell disarray would be brought to normal levels.

The original data were summarized and analyzed by averaging pixel intensity, providing values of the cell intensity, averaging over cells, thus providing a subject intensity and then, finally averaging subject intensities over groups of patients. The means of a “COPD smoker” group and the “COPD only” group were 4.8 +/- 2.1 and 4.0 +/- 2.3, respectively. In order to distinguish between the ‘high’ and ‘decreased’ level of cell disarray, it was felt that a decrease of 25% over the level seen in the ‘high’ group would adequately deem an intervention aimed at reducing Ld as effective. Thus, using the standard, two sided, two sample t-test formulas for sample size, with Type 1 error = 5%, different variances and a power of 80%, for each group, one would need: $n = ({2.1}^{2} + {2.3}^{2}) {(1.96 + 0.84)}^{2} / {(4.8 - 4.0)}^{2} = 119$ Subjects per group.

The next question is: what sample sizes should be selected at lower levels below subject level? This question is related to the specific components of variance which we look into next.

Components of variance and averages across sampling levels

Here we make some simple assumptions. Let X=x be the measurement at the pixel level and assume that it is independent from other observations on the pixel level, with common finite variance $σ_{p i x}^{2}$ . Then the averages across pixels in a cell have the variance given by:

$V a r ({\bar{x}}_{p i x}) = \frac{σ_{p i x}^{2}}{n_{p}}$ (1)

And higher, on the cell level:

$σ_{c e l l}^{2} = σ_{B e t w e e n c e l l s}^{2} + σ_{W i t h i n C e l l}^{2} = σ_{B e t w e e n c e l l s}^{2} + \frac{σ_{p i x}^{2}}{n_{p}}$ (2)

Then the average across cells has variance:

$V a r ({\bar{x}}_{c e l l}) = \frac{σ_{c e l l}^{2}}{n_{c}}$

$\frac{σ_{c e l l}^{2}}{n_{c}} = \frac{1}{n_{c}} (σ_{B e t w e e n c e l l s}^{2} + \frac{σ_{p i x}^{2}}{n_{p}})$ (3)

On the subject level:

$σ_{S u b j e c t}^{2} = σ_{B e t w e e n S u b j e c t s}^{2} + σ_{W i t h i n S u b j e c t}^{2}$ (4)

This can be estimated as:

$V a r ({\bar{x}}_{s u b j e c t}) = \frac{σ_{s u b j e c t}^{2}}{n_{s}}$ (5)

Further giving us:

$V a r ({\bar{x}}_{s u b j e c t}) = \frac{1}{n_{s}} (σ_{B e t w e e n S u b j e c t s}^{2} + σ_{W i t h i n S u b j e c t s}^{2})$ (6)

And since

$σ_{W i t h i n S u b j e c t s}^{2} = \frac{1}{n_{p}} σ_{p i x}^{2}$

$V a r ({\bar{x}}_{s u b j e c t}) = \frac{1}{n_{s}} (σ_{B e t w e e n S u b j e c t s}^{2} + \frac{1}{n_{p}} σ_{p i x}^{2})$ (7)

Finally, the last expression simplifies to a result we will find useful:

$V a r ({\bar{X}}_{s u b j e c t}) = \frac{σ_{B e t w e e n S u b j e c t s}^{2}}{n_{s}} + \frac{σ_{B e t w e e n C e l l s}^{2}}{n_{s} n_{c}} + \frac{σ_{B e t w e e P i x e l s}^{2}}{n_{s} n_{c} n_{p}}$ (8)

Several things are worth noting here.

First, the first summand in the formula above is usually used to estimate the entire expression.
Second, however one determines ns, once it is determined other elements in the equation may be used to minimize, with appropriate constraints, the entire expression for variance.
Finally, one can study the trade-off among three sample sizes above, total variance, and total cost of the experiment.

Sample size justification at lower levels as proportion of total variance of the mean

From established expression for variance of the overall mean across nssubjects, given in equation (8).
We can derive proportion of variability due to subjects so that sample sizes at lower levels guarantee that proportion of total variability due to lower levels is small, say 1% or smaller. This would translate to:

$\frac{σ_{B e t w e e n s u b j e c t s}^{2} + \frac{σ_{B e t w e e n s u b j e c t s}^{2}}{n_{c}} + \frac{σ_{B e t w e e n P i x e l s}^{2}}{n_{c} n_{p}}}{σ_{B e t w e e n s u b j e c t s}^{2}}$ (9)

Notice that ns cancel out from the left hand side, giving the inflation ratio IR:

$\frac{σ_{B e t w e e n s u b j e c t s}^{2} + \frac{σ_{B e t w e e n s u b j e c t s}^{2}}{n_{c}} + \frac{σ_{B e t w e e n P i x e l s}^{2}}{n_{c} n_{p}}}{σ_{B e t w e e n s u b j e c t s}^{2}}$ (10)

IR can be interpreted as the proportional increase in total variance due to lower (nested) levels, and should remain low.

Using $σ_{B e t w e e n S u b j e c t s}^{2} = 0.308$ , $σ_{B e t w e e n C e l l s}^{2} = 0.112$ and $σ_{p i x}^{2} = 2.552$ , observed by Roy et al.,² we numerically compute:

IR = (0.308 + 0.112/nc+2.552/ncnp)/0.308.
For various values of the two unknown sample sizes we can compute the inflation ratio (IR), the following table provides several values of IR of the two sample sizes at lower levels.

For example, if we chose 3 observations per each lower level, we will need to increase subject level sample size by 208%, or from n=119 to n*=250. With 10 observations per lower level we need to increase n by 23.8% or to n*=148, and with 100 observations per level this becomes less than 1%, a very tolerable increase to from n= 119 to n*=120. Cost difference between the processing of a cell and processing of a pixel may add to deciding on optimality discussed in the next section.

Sample size justification involving cost

Snedecor and Cochran³ provide rationale for estimation of sample sizes on various levels using optimization via a cost function. Consider the cost of obtaining all of the samples on three levels as Cost = nscosts +nsnccosts +nsncnpcostp, along with equation (8).

Then, using advanced calculus in derivation, the product:
VC = Variance x Cost (11)
This can be minimized for:

$n_{c} = \sqrt{\frac{\cos t_{s} σ^{2}_{B e t w e e n C e l l s}}{\cos t_{c} σ^{2}_{B e t w e e n S u b j e c t s}}}$ and $n_{p} = \sqrt{\frac{\cos t_{c} σ^{2}_{p i x}}{\cos t_{p} σ^{2}_{B e t w e e n C e l l s}}}$ (12)

Where ns drops out from the equation:
In reality, it is either known beforehand, or found from the usual sample size considerations on the subject level.

To verify these expressions for our data, we use:

$σ_{B e t w e e n S u b j e c t s}^{2} = 0.308$ $σ_{B e t w e e n C e l l s}^{2} = 0.112$ $σ_{p i x}^{2} = 2.552$ and the cost estimates provided below.

We take an educated guess that cost per subject = $1,000, cost per cell = $1, cost per pixel = $0.001. Simple application of formulas above provides:

$n_{p} = \sqrt{\frac{1 \times 2.552}{0.001 \times 0.112}} = 150.94$ (13)

And

$n_{c} = \sqrt{\frac{1000 \times 0.112}{1 \times 0.308}} = 19.01$ (14)

When these two values are used in (Table 1), as 150 and 20 approximately, we see that the total sample size on subject level has to be increased by about 4.2%.

nc	3	5	10	50	10	100	20
np	3	5	10	10	100	100	150
IR%	208	80.8	23.8	4.77	8.93	0.89	4.19

Table 1 Percent increase in the subject level sample size needed for a future study given components of variance from past study in Roy et al.²

If the total sample size previously planned is n=119, the adjusted sample size would be about n*=124 to have similar power. This would translate into a $5,000 additional cost if approximate cost per subject is $1,000, for a total of $129,000 for subject recruitment. For lab work we have 20x$1 + 150x$0.001 =$ 20.15 per subject or 124 x $20.15 = $2,498.6 for all subjects, for the grand total cost of the trial of $131,498.60, assuming the trial drug or treatment is paid for from other resources.

One level of nesting only

In the context of the study described so far, we have cells nested in subjects and pixels nested in cells. Suppose now that pixel level does not exist but that an observation is made on each cell by some other means or some other technology. Then similar formulas follow and are applicable, as presented below.

$V a r ({\bar{X}}_{s u b j e c t}) = \frac{σ_{B e t w e e n S u b j e c t s}^{2}}{n_{s}} + \frac{σ_{B e t w e e n C e l l s}^{2}}{n_{s} n_{c}}$ (15)

The simplified expressions for cost still apply:
Cost = nscosts +nsnccostsand the sample size on lower level, conditional on sample size on higher level is

$n_{c} = \sqrt{\frac{\cos t_{s} σ^{2}_{B e t w e e n C e l l s}}{\cos t_{c} σ^{2}_{B e t w e e n S u b j e c t s}}}$ (16)

Discussion

The effect of nesting on experimental design has been a topic of interest in a vast range of equations in previous literature. Sokal and Rohlf⁴ provide example of an experiment involving drugs, rats, rat livers and readings within livers. Quinn and Keough⁵ provide an example of effect of grazing of sea urchins on percentage cover of filamentous algae. Snedecor and Cochran,³ provide an example of three stage sampling of turnip green plants: the first stage is plants, second stage is leaves within plans, and the third stage is determinations within one leaf. Underwood⁶ provides an example of nested sampling via orchards, trees, branches and twigs. All these examples essentially provide the same solution to the questions raised in this article.

If total available cost of the experiment is provided, sample size on the subject level can be calculated to fit the cost constraints. In clinical trials, however, one usually starts with the sample size on subject level, and not the total cost allowable for the trial. Laboratory or pathology costs are calculated separately and are often unknown.

We then suggest that in designing a trial, one should first get an estimate of variability on each sampling level and calculate sample size on subject level first, obtaining ns. Next we recommend finding an optimal combination of sample sizes on lower levels, following arguments and methods provided in this paper. Finally, we should increase ns as needed to achieve previously planned power.

Conclusion

We have exemplified this method using the lung cancer study in Roy et al. 2010, calculating the sample at each level and cost required to deem a difference between groups as statistically significant. Our resulting power analyses give feasible sample size and cost estimates compliant with our study design.