İn survival analysis, researchers are not interested in a disease per se, its symptoms, diagnostics, treatment or outcomes are not their main concern either. The time, however, the time lapsed to the outcome of a disease, is the main focus of the survival analysis studies. Nevertheless, not for all subjects researchers might observe the event due to various reasons. The subjects might be censored from the study at different time periods: at the end of the course if the event was not observed at all; within the course if the subject was lost to follow-up, or enrolled erroneously. The censoring makes the survival data unfeasible to be analysed with standard non-parametric tests. Kaplan-Meier estimate handles the censored data well, providing in addition to the test results, the survival probabilities and survival curves. On the other hand, Kaplan-Meier estimate does not give us the information on the significance of the difference in the survival of two groups but a few statistical tests specifically used in survival analysis do. The choice of a test is always challenging since there is a fine line between the tests, and the one should have enough expertise and knowledge of the data in hand to be able to identify the assumptions of what test are addressed by the survival data more.

Objectives. The study was aimed to compare the most popular statistical tests used in the course of the survival analysis and, as a result, to choose an appropriate statistical test for the analysis of the data.

Methods. For the survival analysis İBM SPSS Statistics 25 was used. The data consisted of 568 women with the breast cancer divided into two groups based on the ploidy of the tumor cells. Kaplan-Meier method was applied for the estimation of the survival functions in the groups. Wilcohon statistic was found to test the null hypothesis of no difference regarding survival among the aneuploid and diploid groups.

Results. Although, the data had an excessive number of censored subjects. Kaplan-Meier estimate demonstrated that the probability of survival was higher for the diploid group compared to the aneuploid breast cancer. Wilcoxon test demonstrated a statistically significant difference in the survival rates among the subjects of two groups with the lower survival times for the aneuploid group.

Conclusion. The non-parametric tests used in survival analysis require precise consideration due to some peculiarities pertaining to them. Thus, before drawing any inferences on the results of a test a researcher should be confident in the relevance of this test.

Keywords: survival analysis, kaplan-meier estimate, censoring, log-rank test, wilcoxon test, tarone-ware test

Survival analysis is a very specific type of statistical analyses. Survival analysis is aimed to analyze not the event itself but the time lapsed to the event. This time of interest is also referred to as the failure time or survival time. The time used in survival analysis might be measured in different intervals: days, months, weeks, years, etc. The lengthy studies as a matter of course are preferred for being analyzed since they provide stronger evidence and more reliable results. However, it is practically unfeasible for some of the events to be observed over a long period of time. For example, in a study of the pancreatic cancer, one of the most lethal and rapidly growing type of cancer; researchers might get a very low median for survival time, which may indicate that half of the participants died within just a three month period. The studies, perhaps, would not be stopped at the moment of reaching three or six month period and may continue up until five years, but just on the miniscule, if any, number, of participants.

The events in the survival analysis are usually deleterious in nature. The death is the prototypical event for the analysis, termed usually as a failure. Other events, such as an occurrence of a disease, relapse, smoking and drinking resumption, complication of the disease, might be of the research interest as well. The survival analysis methods can be used in other than medicine fields as well: in economics, political science, sociology, engineering.

Survival data require a very particular treatment with caution due to the heterogeneity. The heterogeneity of the data is explained by the fact that subjects of the study might not just experience or do not experience the event but be censored otherwise. The censored subjects remain one of the major challenges for researchers when there is a choice of which statistical methods to apply and how to interpret the results. İn this paper, we aimed to describe the features of survival data in terms of censoring, and to compare the statistical tests used in the survival analysis under different assumptions.

Censorıng and truncatıon

As it was mentioned before, the subjects of the study are often observed not just until the event but until they are dropped out of the study. The latter happens at, so-called, censored survival times. The censored survival times imply the time at which a subject is lost for the observation and the time to the event for him (her) is not recorded. Among the main causes of the censoring are: the non-occurence of an event by the end of the study course; the follow-up termination; and, finally, ‘competing risk’. The follow-up termination can happen either if a patient by himself wishes to terminate the study or due to the loss of a patient’s contact information by the investigators; whereas, the competing risk is simply the occurrence of the other outcome, e.g. a concurrent disease. These reasons relate only to the independent censoring procedure, also called non-informative, as it does not directly affect the survival analysis results. On the contrary, the dependent, or informative, censoring has an adverse impact on the data in terms of the representativeness. For example, a very sick patient might quit a study if it was physically and morally exhausted for him to be examined and followed-up. As a result, the event of the interest that was most likely to happen among such censored patients would be left unobserved.

The censoring might happen in the beginning, at the end, or at any other moment during a study. İf the study finished but the event of the interest was not observed, a participant will be regarded as a right censored. The right-censoring may be a fixed or a random. İf a participant was observed until its endpoind but did not experience the event, it would be considered as s a fixed-right censoring. İn the case when the subject abandoned the course of the study before its end, that is, the event of this hapenning was going unobserved, it would be an example of a random right censoring.

The left censoring relates to the situation when a subject were enrolled into the study despite the event of the interest had already happened before the enrollment. For example, in the research on the cigarette resumption among ex-smokers some of the participants had returned to a bad habit before the study was commenced. The left-type censoring is encountered on rare occasions because investigators are very particular in the selection of participants for the study. Notwithstanding, the left-censoring is not always a matter of an improper selection, but the matter of a sophisticated event detection. For instance, a woman enrolled in the study of different infertility treatments, may be unaware that the pregnancy in fact already happened.

The other cause of a deficient observation of the survival times is the truncation. There are two types of the truncation, left and right. Generally, we deal with the left truncated data related to the late entry of participants to the study for whom the time before the enrollment remains unobserved. These participants did not experience the event by the beginning of the study though, must be all the same differentiated from those subjects free from the event but enrolled at the right time.¹ The late entries may lead to biased results if the investigators equal them with the early entries for which there is no unobserved period.¹ However, the Kaplan-Meier product-limit estimator, used in the survival analysis, handles the left-truncated data successfully.²

Right truncation is made when the event has already occurred for all the participants of the study. Jiang (2011) gives a good example of the study with the right truncated data for the latent period of acquired immune deficiency syndrome (AİDS), when the disease did not manifest itself even though participants had been already infected. Notwithstanding, the right-truncated data could be converted into the left-truncated if the time was traced back to the moment when the event had actually occured.²

Hıstory of survıval analysıs

The survival analysis was named so since the event of the interest in the very first studies was death, that is, whether the subjects would die or survive was the only concern of the analysis.³ As time goes the range of the events of the interest was enlarged, however, the name of the analysis was not altered.

The survival analysis has one of the longest histories among all statistical procedures and methods.⁴ As early as the 17th century, the survival analysis was utilised in demography and actuarial science. The life tables were created firstly in the 18th century for the estimation of mortality rates.¹ Despite сenturies-long history, the survival analysis obtained a scientific framework only in the last century. Paradoxically but the worst stages of human history gave the induce to the human thought and potential. The survival analysis development was brought about by the need to test the military equipment reliability in the World War II.⁵ As a result, the survival analysis which had been concerned only with the mortality before, expanded its use from medicine to other scientific disciplines.⁵

İn this period, the rationale of the life tables, used for a long time before, was called into question by Greenwood and Westergaard.⁴ Afterwards, the life tables were evolved and transformed into the ‘actuarial life tables’ where the discrete time periods of observations were divided into the identical intervals.⁴ The purpose of the actuarial method was to define the proportion of the subjects dying in each interval of time.⁶ This proportion was be found as $\frac{N_{died}}{(N_{total in interval}-N_{censored)}/2)}$ .⁶

According to the formula, one can see that the censored observations contribute only a half to the number of subjects at risk by the time.⁶ Although, the actuarial method is not sensitive to censoring, the assumption of discrete identical time units in the actuarial method continues to be its main shortcoming. Some of the studies are hardly possible to be conducted in the equal time intervals due to several reasons, as for instance financial, or ethical. As a result, the valuable information can be lost and, what is just as important, the researchers encounter a serious dilemma of what method to use if the observations cannot be made in equal time periods (i.e. one week).⁴

Kaplan-Meier method, named after its discoverers, aims to eliminate the drawbacks of the actuarial analysis since it does not require the approximate and identical time of observations.⁴

Kaplan-meıer method

Kaplan-Meier is a non-parametric analysis, also known as the product-limit method, used for estimating the survival function based on the time to the occurrence of the event.⁷ As it was mentioned before, the Kaplan-Meier method copes well with the right-censored and left-truncated observations. The estimator deals with the late entries “through the necessary adjustment for the risk set, the set of individuals alive and under observation at a particular value of the relevant time variable”.⁴ The method is used frequently for comparing the survival times for the subjects with different statuses. The statuses are assigned by the treatment methods or/and circumstances under which they were applied; by some biological, physiological, or/and genetical peculiarities such as gender, age, body mass index, genomic alterations; by the lifestyle, education and socioeconomic level. The group membership of the subjects is predetermined by the status.

Kaplan-Meier estimator has a few assumptions: the survival probability is the same for censored and uncensored subjects; the likelihood of the occurrence of the event is the same for the participants enrolled early and late; the probability of censoring is the same for different groups; finally, the event is assumed to occur at the defined time.⁷

Kaplan-Meier estimator is alternatively named as the product-limit because the unconditional probability of survival to the time, t, is estimated as the product of conditional probabilities of surviving to the different times during the course of a study:

$\hat{S}\left(t\right)={\displaystyle \prod }_{t\left(i\right)\le t}\frac{n_i-d_i}{n_i}, where$

$\hat{S}\left(t\right)$ – is the Kaplan-Meier estimate;

t(i) is the time passed to the next observation from the beginning of the study;

$n_i$ – the number of participants at risk, i.e. still alive participants, at the time i

$d_i$ – number of deaths at time i.

Thus, the total survival probability by a certain time interval is the result of the multiplication of all conditional survival probabilities for the past time intervals. Survival probability for a specific interval is obtained by the number of survivors to the time over the number of subjects at risk to the time. Subjects at risk are ones still remained in the study after some of the participants were censored or died in the preceding time intervals. The time intervals are discrete, so the  varies, however, if it were continuous, the  would be always equal to 1.¹ Kaplan-Meier output tables conceptually are similar to life tables providing a summary on the number of deaths, and number of the subjects at risk or hazard. Although, the tables may be very lengthy for the longitudinal studies with too many time intervals, we can appeal to the survival curves in the results interpretation. Kaplan-Meier curves are graphed in accordance with the probability of the survival for patients free from the event so far, declining in a different manner from the top-left corner to the bottom-right corner.⁸ The results can be graphed for one group or for several groups at the same time. İn the case of a few groups there are curves presented in different colour. The curves can have the same shape or can differ significantly, cross at some point or be parallel. The censored data are also shown on the curves and the way of its illustration depends on the statistical package used (Figure 1).

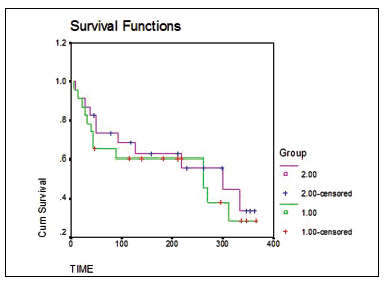
Figure 1 Plots of Kaplan-Meier product limit estimates of survival of a group of patients (as in e.g. 1 and 2) receiving ART and new Ayurvedic therapy for HIV Infection.⁷

At first sight, we can detect the difference in the survival probability by assessing the curves only, but this method is not always informative. The distance between, or some visual deviations in curves might be not statistically significant. For instance, we can make use of the survival curves and compare the median of survival times in the groups of interest. The median time might be determined by drawing a perpendicular from the y-axis to the survival curve at  and then erecting the perpendicular from the x-axis up to the intersection to the same point on the curve. For the demonstration purposes, we used twenty observations of the diploid group drawn from the data provided by Heagerty⁹ on the breast cancer (Figure 2. The median of the survival time for the diploids was approximately 36-37 weeks.

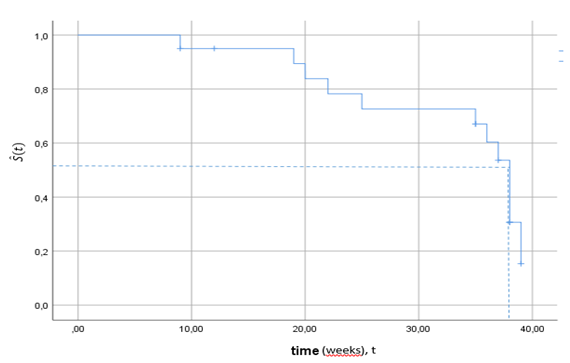
Figure 2 The median survival time for the sample of 15 subjects with the diploid cells tumor drawn from Heagerty (2005) breast cancer data. The median survival time is nearly $\widehat{t_{.5}}=36$  weeks.

İf we had accomplished the same steps for the aneuplod group, and, perhaps, detected the difference in survival times between two groups, but its significance would be questioned. Thus, some statistical tests providing significance level of the results and the areas of acceptance or rejection of the null hypothesis that there is no difference in survival times between groups require to be applied. The use of basic non-parametric tests, based on the rank ordering (such as Mann-Whitney U test or Kruskal-Wallis), for the survival data is practically infeasible because of the censoring.¹⁰ There are some specific non-parametric tests not sensitive to the censored data and therefore widely used in survival analysis. However, it is always matter of dispute which test should to be opted in a particular situation.¹¹

The most commonly known test is a Mantel-Haenszel, or log-rank test, proposed firstly by Mantel in 1966 and then by Cox in 1972. As the result, some researhers refer to the procedure as to the Cox-Mantel test.¹² The test determines the difference between expected and observed number of events in participants of two groups. The test statistic is denoted as Q and distributed as . İt should be noted that the tests are powerful for stratified 2 x 2 tables, and when the number of groups is larger, the pairwise comparison of the hazard rates is carried out.¹² The hazard ratio is an estimate of the hazard rate in the one group relative to the hazard rate in the other group.⁵ If the hazards are proportional, then the ratio will be constant at any interval of time. For example, if the risks of an event for individuals of the one group were twice higher than the hazards in another group at any point of time, the risks of an event would differ double at early or later times as well.¹² Does it mean that we should find the hazard ratio for all individuals during the whole study period and then compare them at different points? İndeed we may do it in a short-term study, but the task is an arduous if there are too many time interval.^1,13 The log-rank test has a very important assumption of proportional hazards to examine. İn a such situation the estimation of survival curves is very useful; one says that if the curves are parallel of the same shape the hazard ratio is constant and logrank test results are reliable.

On the other hand, when the hazard ratio is not constant, the log-rank statistic loses its power to detect the difference in survival probabilities between the groups.¹² Under such circumstances, the Gehan’s generalized Wilcohon procedure should be used.¹⁰ The full name of the statistic is Gehan-Breslow-Wilcoxon test (after Edmund Alpheus Gehan, Norman Edward Breslow and Frank Wilcohon).¹⁴ İt is also called Gehan’s generalized Wilcohon test due to the fact that Gehan generalized the Wilcohon signed rank test to the censored data.¹⁵ The generalized Wilcohon procedure does not require the assumption of the proportional hazards to be met, as a result some scientists use it as the alternative to the Mantel-Haenszel statistic. Nevertheless, the later studies indicated that the Wilcohon test might yield more reliable results for the data with a constant hazard ratio as well. Researchers, however, also found that when the survival curves cross, neither test becomes reliable.¹² An excessive focus on the proportional hazards in the data can lead to the improper use of the test. Hence, Tarone and Ware advise to pay more attention to the period when the most of the events were occurring rather than the equality of the hazards.¹² The Gehan’s generalized Wilcohon test is said to give more weight to the early failures while the log-rank statistic is more suitable for the data with later events.¹²

Similarly to Gehan’s test, Prentice test (also known as Prentice modified Wilcohon test or Peto-Peto-Prentice test) gives more emphasis on the earlier event times and is applied when the proportional hazards assumption is violated.¹⁶ Both tests are powerful when the censoring rates are low and censoring distributions of groups are equal.¹⁶ On the other hand, if this assumption is violated, Peto-Peto-Prentice test is still more powerful than the Wilcoxon test.¹⁶ As it was already mentioned before, when the survival curves cross Mantel-Haenszel, Wilcohon, and Prentice tests do not work well. Tarone-Ware test, for example, can be used instead.¹¹ Perhaps this is the reason why Taron-Ware test is regarded as “superior to the log-rank or Wilcohon tests”.¹⁷ Taron-Ware procedure differs from the latter ones as placing more emphasis on the failures happen somewhere in the middle of the course.¹⁸ On the top of that, Tarone-Ware test is not limited with the number of groups to be applied for, and works well for more than two groups.¹²

Among the diversity of the survival analysis tests, a researcher is challenged to choose the only one relevant while deciding on the statistical significance of results. The process becomes even more complicated if the results of the tests vary.

The data provided by Heagerty⁹ in his manual “Survival data” was examined in this paper. The analysis was aimed to determine whether the ploidy nature of the cancer cells can be a good prognostic factor of the mortality. The participants, the subsample of women from a cohort study of breast cancer, were divivded into two groups according to their ploidy status. The ploidy status is a dischotomous variable with two categories of aneuploid – aneuploid tumor cells, and diploid – for diploid tumor cells. There were 200 women with the aneuploid breast cancer and 368 women with the diploid cell breast cancer in the study. The major shortcoming of the data analyzed was the overwhelming number of the censored observations. The time period was divided into week intervals: from 9 to 120 weeks for the aneuploids, and, from 13 to 120 weeks for the diploids. Since the time intervals in our study as in many other biomedical studies are not organized into equal time intervals, we chose the Kaplan-Meier method for the data analysis. İn our survival data, the early events prevail, therefore Gehan’s generated Wilcohon (Gehan-Breslow-Wilcohon) statistic was chosen to test the null hypothesis that there is no difference in the survival probabilities between the aneuploid the diploid breast cancer groups. We used the SPSS Statistics version 25 in our analysis.

The Kaplan-Meier estimate table, comprising two groups for all time intervals with the survival probabilities and number of subjects at risk, demonstrates that there are too many randomly right-censored subjects in the data: 84.5% of diploids and 76.6% of aneuploids were censored. The median survival times are not shown in the Kaplan-Meier output since there is no subject who had the survival probability of .5 due to the numerous censoring. The table is very long since we have 568 cases which were observed for two and a half years. Thus, it is more conveniently to intepret the survival functions for both of the groups by having a look at the curves. Figure 3 illustrates the survival curves for subject with the aneuplod and diploid types of breast cancer. The curves give a visual representation of the life table given above, so we can see that after the last subject died the survival probability became sligthly less than .6. The curves demonstrate that the survival probability over the study period was higher for the diploids. Hence, women with the diploid type of breast cancer were less likely to experience the event compared to the women with the aneuploid type of tumor cells (Figure 3).

Figure 3 Kaplan-Meier survival curves for the aneuploid and diploid groups.

The SPSS package output also provides the option of the tests for the significance of the difference between the two groups. Researchers, however, still doubt whether the results of all available tests must be presented or just the most relevant one. The relevance of the tests is checked as it was described in the previous sections. We display the results of three tests because all of them signify the statistically significant difference in survival between the groups (p≤.05) (Table 1).

İn order to decide which test result should get the priority, let us look at the curves firstly. The curves are parallel, nearly of the same shape, but does it mean that the proportional hazards assumption is satisfied and we should use the most popular log-rank test? We consider the concept of proportional hazards to be fairly subjective if we assess just curves and too tedious if we do calculations from the table. As it was mentioned before, while making the choice between tests it is important to look at the time period when the events occured to a greater extent. Furthermore, both, so log-rank statistic as Breslow statistic can be used in the case of the proportional hazards. Hence, the proportional hazards assumption is not a crucial one but the period of the events occurence is. The most of the events in our survival data are early events happened in the beginning of the study, whereas in the middle and at the end of the study subjects were mostly censored. Gehan-Breslow-Wilcohon statistic should be estimated in our example as the statistic the most appropriate for the data with proportianl hazards and early period events. Based on the result , we rejected the null hypothesis since the risk of dying is higher for women with the aneuploidy cell breast cancer.

İn survival analysis researchers usually fail to use the conventional non-parametric tests to compare the survival functions among different groups because of the censoring. Kaplan-Meier statistic allows us to estimate the survival rates based on three main aspects: survival tables, survival curves, and several statistical tests to compare survival curves. İn the most of the cases, researchers use the log-rank, or Mantel-Haenszel, test without taking into consideration assumptions behind. However, this test is believed to be powerful only when the hazards of the events are poroportional in the compared groups and when the early events weight more. İn this paper, we revised several statistical tests used in the survival analysis. Each of the test has its own area of application, thus the wrong choice of the statistic can lead to the misrepresentation and misinterpretaion of the results. Although, Gehan-Breslow-Wilcohon test was chosen to signify the difference of the survival between the groups, too many censored cases in the data of this study make the option of the Wilcoxon test disputable to some extent. Thus, the additional studies are required to examine the survival analysis tests on the subject of their sensitivity to different rates and periods of the censoring.

None.

Author declares that there is no conflict of interest.

1. John F. İntroduction to survival analysis. 2014.
2. Jiang Y. Estimation of hazard function for right truncated data (master). Georgia: Georgia State University; 2011.
3. Danacica DE, Babucea AG. Using survival analysis in economics. Survival. 2010;11:15.
4. Dickman P. Survival analysis overview. Biostatistics for Medical and Biomedical Practitioners. 2015.
5. Singh R, Mukhopadhyay K. Survival analysis in clinical trials: basics and must know areas. Perspect Clin Res. 2011;2(4):145–148.
6. Lucijanic M, Petrovecki M. Analysis of censored data. Biochemia Medica. 2012;22(2):151–155.
7. Goel MK, Khanna P, Kishore J. Understanding survival analysis: Kaplan–Meier estimate. İnternational Journal of Ayurveda Research. 2010;1(4):274–278.
8. Jager KJ, Van Dick PC, Zoccali C, et al. The analysis of survival data: the Kaplan–Meier method. İnternational Society of Nephrology. 2008.
9.  Heagerty P. Survival analysis. Lecture notes. 2005.
10. Agarwal GG. Statistics for surgeons – understanding survival analysis. İndian Journal of Surgical Oncology. 2012;3(3):208–214.
11. Karasoy D, Tilki B. Scores and weighted tests used to compare the life curves: Numerical examples. Business & Actueria. 2012;6:1–13.
12. Martinez M. Diagnostics for choosing between Log–Rank and Wilcoxon tests (Ph.D). Western Michigan University. 2007.
13. Rich JT, Neely JG, Wang EW. A practical guide to understanding Kaplan–Meier curves. Otolaryngol Head Neck Surg. 2010;143(3):331–336.
14. Hazra A, Gogtay N. Biostatistics series module 9: survival analysis. İndian Journal of Dermatology. 2017;62(3):251–257.
15. Lou WYW, Lan KKG. A note on the Gehan–Wilcoxon statistic, communications in statistics. Communication in statistics – theory and methods. 1998;27(6):1453–1459.
16. Karadeniz PG, Ercan İ. Examining tests for comparing survival curves with right censored data. Statistics in transition, new series. 2017;18(2):311–328.
17. Willie MM. Analysing of Medical Schemes Complaints by Means of Parametric Proportional Hazard Frailty Models. Public Health Research. 2012;2(1):1–7.
18. Etikan İ, Abubakar S, Alkassim R. The Kaplan Meier Estimate in Survival Analysis. Biom Biostat Int J. 2017;5(2):00128.