
Research Article Volume 5 Issue 6
Bayesian analysis of joint modeling of longitudinal and time to event data using some skew-elliptical distributions
Batoul Khoundabi,1 Anoshirvan Kazemnejad,2
Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Marjan Mansourian,3 Seyed Mohammad Reza Hashemian4
1PhD Student, Department of Biostatistics, Faculty of Medical Sciences, Tarbiat Modares University, IR Iran
2Professor, Department of Biostatistics, Faculty of Medical Sciences, Tarbiat Modares University, IR Iran
3Assistant Professor, Department of Epidemiology and Biostatistics, School of Public health, Isfahan University of Medical Sciences, IR Iran
4Associate Professor, Anaesthetics, Chronic Respiratory Disease Research Center(CRDRC), National Research Institute of Tuberculosis and Lung Diseases (NRITLD), Masih Daneshvari Hospital, Shahid Beheshti University of Medical Sciences, Iran
Correspondence: Anoshirvan Kazemnejad, Department of Biostatistics, Faculty of Medical Sciences, Tarbiat Modares University, Tehran, IR Iran, Tel 98-2182883875, Fax 98-2182884524
Received: August 14, 2016 | Published: May 22, 2017
Citation: Khoundabi B, Kazemnejad A, Mansourian M, et al. Bayesian analysis of joint modeling of longitudinal and time to event data using some skew-elliptical distributions. Biom Biostat Int J. 2017;5(6):239-247. DOI: 10.15406/bbij.2017.05.00153
Download PDF
Abstract
Joint modeling of longitudinal and time to event data have been widely used for analyzing medical data, where longitudinal measurements is gathered with a time to event or survival data. In most of these studies, distributional assumption for modeling longitudinal response is normal, which leads to vulnerable inference in the presence of outliers in longitudinal measurements and violation of this assumption. Violation of the normality assumption can also make the statistical inference vague. Powerful distributions for robust analyzing and relaxing normality assumption, are skew-elliptical distributions, which include univariate and multivariate versions of the student’s t, the Laplace and normal distributions. In this paper, a linear mixed effects model with skew-elliptical distribution for both random effects and residuals and a Cox’s model for time to event data are used for joint modeling. This strategy allows for the skewness and the heavy tails of random effect distributions and thus makes inferences robust to the violation. For estimation, a Bayesian parametric approach using Markov chain Monte Carlo is adopted. The method is illustrated in a real Intensive Care Unit (ICU) data set and the best model is selected using some Bayesian criteria for model selection.
Keywords: joint models, bayesian approach, cox’s proportional model, longitudinal data, time to event data, markov chain Monte Carlo, skew-elliptical distributions
Introducton
Data collected in many clinical and epidemiologic studies, contain both the longitudinal measurements and time to event data. In these studies, usually a biological marker, for example CD4 count measurements in AIDS clinical trials, is considered as a predictor of survival. Also, an interest event such as death or disease progression is considered as an important part of the study. These two types of outcomes often are analyzed using joint modeling of longitudinal and time to event data. Joint modeling has become a progressively popular approach to determine the relationship between of these processes.
Development of joint modeling of longitudinal and time to event data have been discussed broadly in the literature. Hogan and Laird,1 Tsiatis and Davidian,2 Ibrahim et al.3 and McCrink et al.4 give so excellent reviews of models and methods for joint analysis of this type of responses. The most common approach is to suppose that a random effect underlines both longitudinal and survival outcomes as shared parameter models (Henderson et al.5; Hashemi et al.5). Also some other researches are done on Bayesian method (Ibrahim et al.7; Chi and Ibrahim8), nonparametric random effect distributions (Wang and Taylor9; Brown and Ibrahim3), cure fractions (Yu et al.10 Chi and Ibrahim8), multiple longitudinal variables (Lin et al.11), count data (Dunson and Herring12), zero-inflated outcomes (Rizopoulos et al.13), competing risks (Elashoff et al.14), accelerated failure time (Tseng et al.15), parametric assumptions by allowing flexible longitudinal trends (Brown et al.16). In joint modeling of longitudinal and survival data a mixed effects model is often used for analyzing longitudinal response of joint modeling. This part maybe incomplete due to dropout, where dropout mechanism (Diggle and Kenward17) can be considered or with some reasons ignored.
The traditional treatment, in many statistical models in particular mixed effect models contexts, is that the random effects follow the multivariate normal distribution (Verbeke and Lesaffre,18 Rosa et al.19). In practical applications, this assumption is likely to be failed if, for example, potential outliers exist in the data set.
The normality may be a reasonable model for many problems with continuous measurements, in other situations the normality assumption on a transformed scale is, at best, hoped for. Although such methods may give sensible empirical results, they should not be used if a more suitable theoretical model can be found. Some reasons for this are: (i) transforming usually prepares reduced information on an underlying data generation mechanism; (ii) the transformations are commonly applied to each component one by one, and joint normality is not secured; (iii) the interpretation based on transformed variables are more difficult, especially when transformations are various for the different proportions; (iv) multivariate homogeneity often requires a different transformation from the one to get normality; and (v) a model derived for a given data set may not be relevant to subsequent data sets.
Parametric robust analyses are statistical methods based non normal assumption for adjustment of usual statistical methods in the presence of outliers. The use of heavy-tailed distribution in mixed effects model for robust analysis is valuable for adjusting the role of outlier individuals in the sample and is widely applied in the literature, for example: Rosa et al.,19 Lange et al.20] and Wu.21
A common approach for robust inference is to replace the multivariate t-distribution, which has heavier tails than the normal (Lange and Sinsheimer,22 Pinheiro et al.23). There are, however, many other situations when the underlying distribution no longer satisfies the symmetric property (e.g., Zhang and Davidian).24 Robust joint modeling can be found in Li et al.25 and Huang et al.26 where a student’s t distribution in different structures of joint modeling of longitudinal and survival data is applied. Thus alternative flexible distributions, such as the multivariate skew-elliptical (SE) distribution, are proposed in recent studies (Azzalini and Capitanio,27 Ma et al.,28).
In this paper, we have developed robust inference of joint modeling of longitudinal and time to event data using skew-elliptical distributions (Lange and Sinsheimer).22 These distributions include the skew student’s t (ST), the skew slash (SS), skew Laplace (SL) and the skew normal (SN) distributions. We consider a linear mixed effect model with skew-elliptical distribution assumption for longitudinal response modeling. Also, a Cox proportional hazard model with step baseline hazard in a frailty model structure is chosen for survival response modeling.
We have used Bayesian approach and the available software OpenBUGS (Spiegelhalter et al.)29 for implementation of the models, where Bayesian criteria of DIC (deviance information criterion has been used for model selection. In application section, we have reanalyzed an ICU data set and we present a strategy, in a Bayesian perspective, and show that these skewed distributions are more appropriate than the commonly used distributions.
The rest of the article is organized as follows: In Section 2, some SE distributions are briefly introduced. In Section 3, the specification of joint models as a shared parameter model and Bayesian hierarchical joint models when the random effect terms follow SE distributions. This is done by the Gibbs sampling implementation. In Section 4, we describe the real data set on the hospitalized patients in ICU and subsequently present a Bayesian analysis of the data set. The McMC scheme and statistical interpretation are given in Section 5. Finally, discussions and concluding remarks are illustrated in Section 6.
Multivariate SE distributions
Several versions of the multivariate SE distributions have been offered in the literature and some of them have recently been used in the univariate mixed effect models (Gosh et al.,30 Jara et al.31). Here, we utilize the multivariate SN and ST distributions introduced by Sahu et al.32 and extended by others (Arellano-Valle and Genton).33 We also make use of the multivariate Laplace distribution and its skewed version proposed by Arsla.34 These distributions are shown to be a scaled mixture of normal that produces flexible distributions with, for example, heavier tails than the multivariate normal distribution.
The multivariate SN distribution
In general, the p-variate Y follows the SN distribution with location vector μ, scale matrix ∑ , and
skewness matrix
if the probability density function (pdf) of Y is given by
(1)
where
,
is the pdf of
evaluated at y and
denotes the cumulative density function (cdf) of the p-variate standard normal distribution (Sahu et al. [32]). We denote the density by
. If D = 0 density (2) reduces to the usual symmetric multivariate normal distribution. The mean and variance of Y are given by
and
,
where
.
The multivariate ST distribution
The p-variate Y follows the ST distribution with location vector μ, scale matrix ∑ , degree of freedom ν, and
skewness matrix
if the pdf of Y is given by
(2)
Where
,
is the pdf of student’s evaluated at y, and
denotes the cdf of the p-variate standard t distribution with degrees of freedom
(Sahu et al. [32]). We denote the density by
. As SN, If D = 0, then density (3) reduces to the usual symmetric multivariate student’s t distribution. As ν tends to infinity and D = 0, then the distribution reduces to the multivariate normal. The mean and the variance of Y are shown to be
and
The multivariate SL distribution
The p-variate Y follows the SL distribution with location vector μ, scale matrix ∑ , and
skewness vector
if the pdf of Y is given by
(3)
Where
(Arslan, [31]). We denote the density by
. If D = 0, then (4) reduces to the density function of the multivariate symmetric Laplace distribution. The mean and the variance of Y are shown to be
and
.
Specification of joint modeling
The longitudinal part of the joint model can be described as follows. Let
denote the value of longitudinal measurement, at time point t for the
individual
. The observed times are
,
. Thus, the observed longitudinal data for the
individual consist of measurements
. For the longitudinal process, we consider the following linear mixed effect model
(4)
where components of
are measurement errors,
is a
-dimensional vector of longitudinal fixed-effect parameters.
is a
-dimensional vector of random effects and is independent of
.
and
are, respectively,
-dimensional and
-dimensional explanatory variables. Let
denote the observed survival time for the
individual,
, which is taken as the minimum of the true event time
and the censoring time
, i.e.,
. We define a censoring indicator,
, which is 0 for right-censored and 1 for complete observed individuals. Therefore, the observed data for the time to event consist of the pairs
.
For the time to event process, we consider a semiparametric proportional hazard model in a frailty structure.
The hazard function in our proposed model is given by:
(5)
where
is the baseline hazard function. Thus, the density function of survival time for
individual can be written in the form:
(6)
Where
,
and
are
and
dimensional vectors of explanatory variables, respectively.
is a
-dimensional vector of time to event fixed effect parameters, and
is a
dimensional of random effects of time to event process. It is important to note that some elements of
and
are shared between two models and joint modeling is formed using this structure.
Suppose that
,
,
.
We further assume that the baseline hazard is a step function,
, for
, where
is a partition of (0,∞) and K indicates the number of steps for the baseline hazard, also
. Therefore the cumulative baseline hazard is given by
(7)
We implement the Bayesian methodology using MCMC techniques for the joint modeling of longitudinal and survival data with SE distributional assumption. ST distribution was used for random effects terms distribution in tow longitudinal and survival models because of more parameters than other distribution. Inference based on the another distribution will be similar. Multivariate SE distributions will be reconstructed by the mixing strategy approach, therefore they are very convenient to implement in the Bayesian framework. A key characteristic of this model, which allows writing BUGS codes, is that it can be expressed in a flexible hierarchical representation. For example by using multivariate ST distribution for
, hierarchical representation can be followed:
……………. (8)
Bayesian specification of the model needs to consider prior distribution for all the unknown parameters. In our modeling
is the unknown vector of parameters and because of not having any prior information from historical data or previous experiment, we try to assign non-informative prior distributions for the parameters. Assuming elements of the parameter vector to be independent, the prior distributions are given by:
…. (9)
where
follows inverted gamma,
and
are assumed to be normally distributed,
and
were denoted by inverse-Wishart distribution,
and
distributions are assumed truncated exponential distribution and in final truncated normal distribution for
and
are determined. The hyper parameters of these priors are selected so that they lead to the non-informative prior distributions.
According to
the joint posterior density of all unobservable is given by :
…. (11)
The above described joint posterior distribution is analytically intractable but MCMC methods such as the Gibbs sampler and Metropolis-Hastings algorithm can be used to draw samples, from which features of marginal posterior distribution of interest can be inferred. The Gibbs sampler works by drawing samples iteratively from conditional posterior distributions deriving from (11). For this purpose, we have needed all full conditional distribution. Let
, and let
is one of the component of it, we define
for the above-mentioned vector when v is omitted from it. The full conditional distributions for
,
and
, respectively, have the form:
and
and
For
and
, i = 1, 2, ...,n the full conditional distributions have closed form, and are given
by:
where
and
,
also
where,
and
The full conditional distributions of
,
,and
are not in closed forms of known distributions. Thus, the Gibbs sampling can readily be implemented. For these parameters a Metropolis-Hastings can be embedded in the Gibbs sampling scheme to obtain draws for them. The full conditional distributions of
,
and
are presented in Appendix1.
Applications
We analyzed the data from a retrospective cohort study. All consecutive adult patients (N=380) were considered who, from October 2010 through October 2012, underwent cardiac surgical procedure with cardiopulmonary bypass at Masih Daneshvari Hospital,Tehran, Iran as a referral center. Patients who underwent more than one cardiac surgical procedure during hospitalization (n=40), were excluded from the study. Additional exclusion criteria were surgeries performed off-pump (n=15) and preoperative renal failure requiring dialysis (n=25). Overall, 300 patients could be included in the study. After surgery, patients were admitted to the intensive care unit (ICU) and were followed from the day of ICU admission until ICU discharge or end of study. Urine output (UO) and other physiological variables were repeatedly measured in 2 hours in the first 8 hours of admission in ICU. Patients’ demographics and laboratory data were gathered repeatedly. Main survival endpoint was the time of occurrence of acute kidney injury (AKI) after cardiac surgery that was defined, the amount of urine output less than 0.5 ml/kg per hour in first 6 hours. Patients were followed since ICU admission until AKI occurrence.
We have used the joint modeling which fitted by Guo and Carlin,35 but with some various distributional assumptions. The aim of fitting joint models is to additionally study the relationship between two longitudinal and time to event responses in terms of available covariates. Parameter  in our joint model is determined to assessment relationship strength between UO and AKI occur hazard. The joint modeling with random intercept and slop is given by:
in our joint model is determined to assessment relationship strength between UO and AKI occur hazard. The joint modeling with random intercept and slop is given by:
For the time to event process, we have applied a Cox proportional hazard model; the hazard function for this model is given by:
the random effects,
, are shared between two models. Random effects are assumed to have a bivariate skew elliptical distribution, that is,
. In this model,
is the
measurement urine output on the
individual in the study,
and i : 1, 2, ...,m.
is a gender indicator (0=male, 1=female), also other three explanatory variables are
(0=no, 1= yes),
(0=no, 1=yes), and
(0=no, 1=yes).
score and DBP mean Acute Physiology and Chronic Health Evaluation II score and diastolic blood pressure.
In the Bayesian MCMC method, we ran two parallel MCMC chains with different starting values for each 100,000 iteration. Then, we discarded the first 40, 000 iterations as pre-convergence burn-in and retained 50, 000 as the posterior analysis.
In all models,
,
and
where, k = 1, 2, p1 = 6, p2 = 6, and
∼ IW(I2, 2). The hyper parameter of student’s t,
, is assumed to have U(1, 7) distribution. For the piecewise baseline hazard function [
,
(the number of piecewise baseline=4)] the gamma (2, 2) prior distribution is considered.
Hyperparameters are chosen such that the priors of the parameters tend to be weakly informative. The implementation of this method is relatively easy in the publicly available software Open BUGS (Spiegelhalter et al. 2003). The parameter estimates are not sensitive to the choice of hyperparameters and initial values. In order to see how stable the final estimates are, multiple parallel chains with different initial values should be carried out (we considered two chains).
Figure 1 shows the observed longitudinal measures of UO plotted against time for the patients included in the analysis based on the AKI occurrence. UO decreases over time and it seems censoring mechanism be randomly, hence tow graphs have similar pattern.
Figure 1 Profile UO measurements over time (a) The individuals with censored survival time (b)The individuals with non-censored survival time.
In total, our results were organized on 10 different models, 9 models in all combinations of three distribution SN, ST and SL for for
and
, In addition to normal assumption for both of them table 1. In this table for example SN,SL model shows skew elliptical normal distribution for shared random effects and skew elliptical Laplace distribution for the residuals. The estimated random effects distribution surface and estimated residuals distribution histogram in N,N model, are depicted in Figure 2 (a) , (b) respectively. The plots clearly show deviation from bivariate normality distribution in shared random effects and normally distributed residuals. According to DIC criteria the model with bivariate skew t and skew Laplace distribution for shared random effects and residuals respectively (ST,SL), is the best-fitted model for the data, while (ST,ST) model is the second-best model.
Model |
|
|
|
DIC |
N,N |
6405.75 |
6044.85 |
360.9 |
6766.65 |
SN,SN |
5709.11 |
5241.32 |
467.79 |
6176.9 |
ST,SN |
5559.66 |
5048.98 |
510.68 |
6070.34 |
SL,SN |
5990.38 |
5601.93 |
388.45 |
6378.83 |
SN,ST |
5799.42 |
5369.05 |
430.37 |
6229.79 |
ST,ST |
5202.03 |
4668.69 |
533.34 |
5735.37 |
SL,ST |
5990.12 |
5603.99 |
386.13 |
6376.25 |
SN,SL |
5695.6 |
5215.05 |
480.55 |
6176.15 |
ST,SL |
5039.34 |
4486.56 |
552.78 |
5592.12 |
SL,SL |
5830.4 |
5440.13 |
390.27 |
6220.67 |
Table 1 Bayesian model selection for the ICU data set
SN, SL: shows skew elliptical normal distribution for shared random effect and Skew elliptical Laplace distribution for residuals.
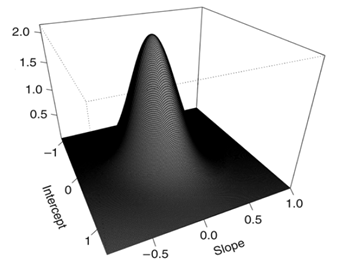
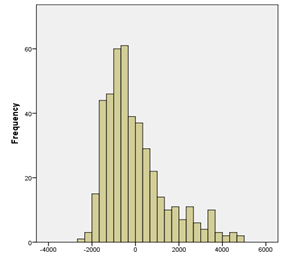
Figure 2 (a) Estimated random effects distribution under the multivariate normal distribution fitted to the ICU data. (b) Histogram of residual estimates.
Parameters |
mean |
SD |
median |
95% HPD |
Intercept (
) |
8.236 |
0.415 |
8.123 |
(8.117,8.780) |
Time ( β12) |
-0.201 |
0.030 |
-0.201 |
(-0.242,-0.164) |
Age ( β13) |
1.500 |
1.101 |
1.500 |
(-0.926,1.695) |
Sex(β14) |
-0.040 |
0.010 |
-0.045 |
(-0.009,0.049) |
DBP (β15) |
3.653 |
1.838 |
3.474 |
(3.257, 3.807) |
Infection (β16) |
-0.386 |
0.221 |
-0.399 |
(-0.721, 0.053) |
Intercept (β21) |
-1.779 |
0.799 |
-1.774 |
(-3.235,0.368) |
APACHE II score (β22) |
0.439 |
0.275 |
0.431 |
(2.925, 4.996) |
Sex (β23) |
-0.646 |
0.393 |
-0.673 |
(-2.414, 0.779) |
DBP (β24) |
-0.216 |
0.088 |
-0.229 |
(-0.356, -0.179) |
Hospital length of stay (β25) |
0.765 |
0.674 |
0.765 |
(1.201, 1.832) |
Emergency surgery(β26) |
0.612 |
0.425 |
0.621 |
(-0.736, 0.792) |
γ |
-0.310 |
0.211 |
-0.315 |
(-0.611, -0.288) |
βb0 |
0.430 |
0.311 |
0.401 |
( 0.119, 0.564) |
|
-0.012 |
0.004 |
-0.011 |
(-0.204, 0.178) |
ϑb |
11.199 |
6.108 |
11.199 |
(5.691, 18.344) |
|
0.073 |
0.082 |
0.070 |
(0.039,0.048) |
|
0.147 |
0.099 |
0.147 |
(0.119,0.188) |
|
0.067 |
0.055 |
0.070 |
(0.049,0.098) |
|
0.031 |
0.022 |
0.031 |
(0.009,0.051) |
h1 |
9.50e-04 |
9.86e-04 |
7.31e-04 |
(4.716e-08, 0.004) |
h2 |
10.10e-04 |
10.06e-04 |
7.90e-04 |
(4.918e-08, 0.009) |
h3 |
0.692 |
0.952 |
0.627 |
(6.796e-06, 2.136) |
h4 |
1.211 |
1.001 |
1.196 |
(6.237e-05, 3.985) |
Table 2 Bayesian parameter estimates (posterior mean, median and standard deviation, SD) and 95% HPD for analyzing the ICU data set
Table 2 includes parameter estimates and %95 highest posterior density intervals for parameters of (ST, SL) model for the ICU data set. According to the results of the mixed model of joint analysis, a decrease of UO occurred more in infected patients and also in low DBP, significantly. The total number of UO longitudinal measurements was 1540 and the average of measurements was 3.85 per patients. Low DBP (HR=1.2) and higher hospital length of stay (HR=2.0) had significant effects on the risk of AKI after cardiac surgery, similar results were obtained by other researchers such as: Kim and et al.,36 Khwaja.37 After using joint modeling, our findings showed a negative significant association between the risk of AKI following cardiac surgery and UO in patients (
= -0.31), that expressed the suitable selection of the joint modeling for this research.
Discussions and concluding remarks
Joint modeling of longitudinal and survival data provides a suitable tools for the analysis of relationship between tow responses. In this paper, flexible joint modeling of these responses is proposed to deal with the situations in which the underlying distributions follow asymmetric structures. We fitted some flexible models for an empirical example taken from a retrospective cohort study to illustrate the suggested strategy. In most studies, the random effects and residuals terms vector is taken to be normally distributed. However, in the analysis of ICU data, we showed that this assumption was violated, leading to inappropriate results. Thus, we applied suitable non-normal distributions to avoid model mis-specifications.
We have used the Cox proportional hazard model for time to event process and a linear mixed effect model for longitudinal measurements. These two models have joined by a vector of random effects which shared in some components together.
In this study, we assessed the association between UO and AKI using the joint modeling of longitudinal and survival data for first time.
After using joint modeling, our findings showed a negative significant association between the risk of AKI following cardiac surgery and UO, which expressed the suitable selection of the joint modeling for this research. Also significant skewness parameter for random intercept implied accurate choice in skew distribution for random effects. According to the results of the mixed model of joint analysis, a decrease of UO occurred more in female and infected patients and also in low DBP, significantly.
In survival part, Female gender, older age, high APACHE II score, low DBP, long hospitalization and emergency surgery had significant effects on the risk of AKI after cardiac diseases. Similar results were obtained by other researchers such as: Kumar,38 Bagshaw39 and Kim.36 Sepsis was also introduced as considerable risk factors of AKI. Majority of infected patients were septic in this study, Hashemian.40 Many other factors are associated with an increased risk of AKI but their influence will be highly dependent on the specific nature of the population, Brochard et al.41
However, the occurrence of AKI after cardiac surgery is often not rapid and other factors concerning intra operative and postoperative management of patients could be relevant. We recommend definite prevention programs in the ICU target patients with traditional risks of AKI such as older age, sex, cardiovascular surgery, chronic pulmonary disease etc.42–55
Acknowledgements
The authors are grateful to the reviewers for their constructive comments that improved the manuscript.
Conflicts of interest
References
- Hogan JW, Laird NM. Model-based approaches to analyzing incomplete longitudinal and failure time data. Stat Med. 1997;16(1–3):259–272.
- Tsiatis AA, Davidian M. A semi parametric estimator for the proportional hazards model with longitudinal covariates measured with error. Biometrika. 2001;88(2):447–458.
- Brown ER, Ibrahim JG. A Bayesian semi parametric joint hierarchical model for longitudinal and survival data. Biometrics. 2003;59(2):221–228.
- Mccrink K, Spelke ES, Dehaene S, et al. Non-symbolic halving in an Amazonian indigene group. Developmental Science. 2013;16(3):451–462.
- Henderson R, Diggle P, Dobson A. Joint modeling of longitudinal measurements and event time data. Biostatistics. 2000;1(4):465–480.
- Hashemi RH, Jacqmin-Gadda, Commenges D. A latent process model for joint modeling of events and markers. Lifetime Data Anal. 2003;8(4):335–348.
- Ibrahim JG, Chen MH, Sinha D. Bayesian Survival Analysis. Springer- Verlag, US; 2002.
- Chi YY, Ibrahim JG. Joint models for multivariate longitudinal and multivariate survival data. Biometrics. 2006;62(2):432-445.
- Wang Y, Taylor JMG. Jointly modeling longitudinal and event time data with application to acquired immunodeficiency syndrome. Journal of the American Statistical Association. 2001;96(455):895–905.
- Yu M, Law NJ, Taylor JMG. Joint longitudinal survival cures models and their application to prostate cancer. Statistica Sinica. 2004;14:835–862.
- Lin H, McCulloch CE, Mayne ST. Maximum likelihood estimation in the joint analysis of time-to-event and multiple longitudinal variables. Stat Med. 2002;21(16):2369–2382.
- Dunson DB, Herring AH. Bayesian latent variable models for mixed discrete outcomes. Biostatistics. 2005;6(1):11–25.
- Rizopoulos D, Verbeke G, Lesaffre E, et al. A two-part joint model for the analysis of survival and longitudinal binary data with excess zeros. Biometrics. 2008;64(2):611–619.
- Elashoff RM, Li G, Li N. A joint model for longitudinal measurements and survival data in the Presence of multiple failure types. Biometrics. 2008;4(3):762–771.
- Tseng YK, Hseih F, Wang JL. Joint modeling of accelerated failure time and longitudinal data. Biometrika. 2005;92(3):587–603.
- Brown ER, Ibrahim JG, DeGruttola V. A flexible B-spline model for multiple longitudinal biomarkers and survival. Biometrics. 2005;61(1):64–73.
- Diggle PJ, Kenward MG. Informative dropout in longitudinal data analysis (with discussion). Journal of the Royal Statistical Society Series C (Applied Statistics). 1994;43(1):49–93.
- Verbeke G, Lesaffre E. The effect of misspecifying the random-effects distribution in linear mixed models for longitudinal data. Computational Statistics & Data Analysis. 1997. p. 541–556.
- Rosa GJM, Padovani CR, Gianola D. Robust linear mixed models with normal/independent distributions and Bayesian MCMC implementation. Biometrical Journal. 2003;45 (5):573–590.
- Lange KL, Little JA, Taylor MGJ. Robust statistical modeling using the t distribution. Journal of the American Statistical Association. 1989;84:881–896.
- Wu L. Mixed Effects Models for Complex Data. Chapman, Hall, editors. Taylor & Francis, CRC Press, USA; 2010.
- Lange KL, Sinsheimer JS. Normal/independent distributions and their applications in robust regression. Journal of Computational and Graphical Statistics. 1993;2(2):175–198.
- Pinheiro JC, Liu CH, Wu YN. Efficient algorithms for robust estimation in linear mixed-effects models using the multivariate t distribution. Journal of Computational and Graphical Statistics. 2001;10(2):249–276.
- Zhang D, Davidian M. Linear mixed models with flexible distributions of random effects for longitudinal data. Biometrics. 2001;57(3):795–802.
- Li N, Elashoff RM, Li G. Robust Joint Modeling of Longitudinal Measurements and Competing Risks Failure Time Data. Biom J. 2009;51(1):19–30.
- Huang X, Li G, Elashoff RM. A joint model of longitudinal and competing risks survival data with heterogeneous random effects and outlying longitudinal. Stat Interface. 2010);3(2):185–195.
- Azzalini A, Capitanio A. Statistical applications of the multivariate skew normal distribution. Series B Statistical Methodology. 1999;61(3):579–602.
- Ma J, Plesken H, Treisman JE, et al. Lightoid and Claret: a rab GTPase and its putative guanine nucleotide exchange factor in biogenesis of Drosophila eye pigment granules. Proc Natl Acad Sci U S A. 2004;101(32):11652–11657.
- Spiegelhalter DJ, Thomas A, Best N, et al. Win BUGS Examples, MRC Biostatistics Unit, Institute of Public Health and Department of Epidemiology and Public Health, Imperial College School of Medicine, UK, 2003.
- Ghosh SK, Hajra S, Jayaram M. Faithful segregation of the multicopy yeast plasmid through cohesin-mediated recognition of sisters. Proc Natl Acad Sci U S A. 2007;104(32):13034–13039.
- Jara A, Mezzano S. Vascular damage in chronic kidney disease. Rev Med Chil. 2008;136(11):1476–1484.
- Sahoo R, Sengupta R, Ghosh S. Nitrosative stress on yeast: inhibition of glyoxalase-I and glyceraldehyde-3-phosphate dehydrogenase in the presence of GSNO. Biochem Biophys Res Commun. 2003;302(4):665–670.
- Arellano-Valle RB, Genton MG. On fundamental skew distributions. Journal of Multivariate Analysis. 2005;96:93–116.
- Arslan E, Mack W, Eraslan AN. Transient heating of a rotating elastic-plastic solid shaft. 2008;8(1)::0257–10258.
- Guo X, Carlin BP. Separate and Joint Modeling of Longitudinal and Event Time Data Using Standard Computer Packages. The American Statistician. 2004;58(1):16–24.
- Kim MY, Park JH, Kang NR, et al. Increased risk of acute kidney injury associated with higher infusion rate of mannitol in patients with intracranial hemorrhage. J Neurosurg. 2014;120(6):1340–1348.
- Khwaja A. KDIGO clinical practice guidelines for acute kidney injury. Nephron Clin Pract. 2012;120(4):c179–c184.
- Kumar AB, Suneja M. Cardiopulmonary bypass-associated acute kidney injury. Anesthesiology. 2011;114(4): 964–970.
- Bagshaw SM, George C, Gibney RN, et al. A multi-center evaluation of early acute kidney injury in critically ill trauma patients. Ren Fail. 2008;30(6):581–589.
- Hashemian S, Jamaati HR, Malekmohammad M, et al. Assessing the performance of two clinical severity scoring systems in the ICU of a tertiary respiratory disease center. Tanaffos. 2010;9(3):58–64.
- Brochard L, Abroug F, Brenner M, et al. An official ATS/ERS/ESICM/SCCM/SRLF statement: prevention and management of acute renal failure in the ICU patient: an international consensus conference in intensive care medicine. Am J Respir Crit Care Med. 2010;181(10):1128–1155.
- Acuna E, Rodriguez CA. Meta-analysis study of outlier detection methods in classification, Technical paper, University of Puerto Rico at Mayaguez, Retrieved from academic.uprm.edu/ eacuna/ paperout.pdf. In proceedings IPSI 2004, Italy. 2004.
- Brooks SP. Discussion on the paper by Spiegelhalter Best Carlin and vande Linde, Journal of the Royal Statistical Society Series B 2002;64:3616–3618.
- Carlin P, Louis TA. Bayes and Empirical Bayes Methods for Data Analysis. second edition. Chapman & Hall, CRC Press, New York; 2000.
- Chen MH, Ibrahim JG, Sinha D. A new joint model for longitudinal and survival data with a cure fraction. Journal of Multivariate Analysis. 2004;91:18–34.
- Chi YY, Ibrahim JG. Bayesian approaches to joint longitudinal and survival models accommodating both zero and nonzero cure fractions. Statistica Sinica. 2007;17:445–462.
- Gelman A, Rubin DB. Inference from Iterative Simulation Using Multiple Sequences. Statistical Science. 1992;7(4):457–511.
- Geweke J. Evaluating the accuracy of sampling-based approaches to calculating posterior moments. In: Bernado JM, editors. Bayesian Statistics, Clarendon Press, UK; 1992 p.
- Geweke J. Bayesian treatment of the independent Student-t linear model. Journal of Applied Economic. 1993;8:19–40.
- Goldman AI, Carlin BP, Crane LR, et al. Response of CD4+ and Clinical Consequences to Treatment Using ddI or ddC in Patients with Advanced HIV Infection. J Acquir Immune Defic Syndr Hum Retrovirol. 1996;11(2):161–169.
- Heidelberger P, Welch PD. Simulation run length control in the presence of an initial transient. Operations Research. 1983;31(6):1109–1144.
- Ibrahim JG, Chen MH, Sinhav D. Bayesian methods for joint modeling of longitudinal and survival data with application to cancer vaccine trials. Statistica Sinica. 2004;14:863–883.
- Iglewics B, Martinez J. Outlier Detection using robust measures of scale. Journal of Statistical Computation and Simulation. 1982;15(4):285–293.
- Little RJA. Robust Estimation of the mean and covariance matrix from data with missing values. Journal of the Royal Statistical Society. Series C (Applied Statistics). 1988;37(1):23–38.
- Spiegelhalter DJ, Best NG, Carlin BP, et al. Bayesian measures of model Complexity and fit. Journal of the Royal Statistical Society: Series B (Statistical Methodology). 2002;64(4):583–639.

©2017 Khoundabi, et al. This is an open access article distributed under the terms of the,
which
permits unrestricted use, distribution, and build upon your work non-commercially.


![]() in our joint model is determined to assessment relationship strength between UO and AKI occur hazard. The joint modeling with random intercept and slop is given by:
in our joint model is determined to assessment relationship strength between UO and AKI occur hazard. The joint modeling with random intercept and slop is given by:

