eISSN: 2378-315X


Research Article Volume 10 Issue 4
1Professor, Department of Mathematics, School of Sciences, Noida International University, G.B. Nagar, India
2Department of Community Medicine, Noida International Institute of Medical Sciences, Noida International University, G.B. Nagar, India
3Assistant Professor, Department of Medicine, Noida International Institute of Medical Sciences, Noida International University, G.B. Nagar, India
4Professor & HOD, Department of Community Medicine, Noida International Institute of Medical Sciences, Noida International University, G.B. Nagar, India
5Associate Professor, Department of Statistics, Assam University, Silchar, India
Correspondence: Kamlesh Kumar Shukla, Professor, Department of Mathematics, School of Sciences, Noida International University, G.B. Nagar, India
Received: October 18, 2021 | Published: December 15, 2021
Citation: Shukla KK, Rahman SA, Singh R, et al. ARIMA model for COVID-19 and its prediction in India. Biom Biostat Int J. 2021;10(4):176-183. DOI: 10.15406/bbij.2021.10.00345
In this paper, autoregressive integrated moving average (ARIMA) model has been applied to know the trend and to predict future pattern of present COVID-19 in India. Accuracy of the model has been checked. Data from July 1, 2020 to August 3, 2021 has been taken for the study. We estimated ARIMA model to forecast the epidemic trend over the period after July 1, 2020, by using the Indian epidemiological data (www.COVID19india.org)1 at national level. The data refer to the number of daily confirmed, total confirmed and deceased cases officially registered by the Indian Ministry of Health (https://api.COVID19india.org/) for the considered period. The main aim of this study is to know the trend of COVID-19 daily cases as well as deceased cases, and forecast for next 120days after August 3, using appropriate ARIMA model.
Keywords: ARIMA, COVID19, KPSS-test, PP-test, MSE, ME, Confirmed cases
The pandemic COVID-19 is initially recognized in China and could be traced back to a cluster of severe pneumonia cases identified in Wuhan, China in December 2019,2,3 and after two months it starts spreading in the world. Almost all countries in the world are affected by COVID-19 and still going on its transmission from person to person, city to city, nation to nation. It has been affecting not only the health of persons but social- economic status of person, city as well as nation.
As we all know that a COVID-19 case has been started in India approximately in the month of January 2020 and thereafter spreading rapidly. Spread of this disease through human to human contact, a large number of cases have been reported worldwide by Hamzah, et al.4 Due to the outbreak of this pandemic, an obligatory situation was formed, whereby the authorities of various countries and continents had to put restrictions on the movement of people and non-essential activities. Some of these restrictions included imposing of lockdowns, maintaining social distancing, and work from home in academics and in business continuity plans. Thus, the spread of COVID-19 has left a major impact on the environment as well as on the lifestyle of human beings.5,6 Almost all academic institutions were closed and people were advised to work from home, and perform contactless financial transactions using various digital platforms,7,8 In this way socio-economic status of a country has been affected.
The total number of confirmed, active, recovered and deceased cases were 203,456,777, 16,375,542, 182,773,747 and 4,307,488 recorded in the world as well as 3,19,69,596, 3,96,694 3,11,31,926, and 4,28,339 were recorded in India till August 8, 2021. As far as India is concerned, it is very challenging task to control/manage COVID-19, where the population is around 1.38billion. As we know that India has produced two vaccinations and started vaccinate to the people from January, 2021 onward. Although there is some restrictions and limitations of age of persons due to shortage of vaccinations, but Vaccination may also have impact in reducing the cases of novel corona virus.
Many researchers have studied on COVID-19 cases and applied different forecasting models such as Trigonometric Exponential Smoothing State Space model with Box-Cox transformation (TBAT) developed by De Livera, et al.9 uses a combination of Fourier terms with an exponential smoothing state space model and a Box-Cox transformation,, Multiple Regression, ARIMA etc., but we applied optimum ARIMA model to predict future cases for four months because it was observed from the literature that ARIMA model is good model in terms of projection and it is having less error in comparison to other. To understand the future spread of pandemic and to devise management strategies, various models have been designed, which give information regarding the time of attainment of infection peak, the number of infected cases and the requirement of medical infrastructure to manage the spread.10
The main objectives of this study are: It can be easily identified the trend of COVID19 in India using ARIMA models. Its trend and forecast will be benefited to all governmental institutions, especially in public health for making further policy and plan. This study may be used to monitor the epidemic and to better allocation of the resources. Further useful and more precise forecasting may be provided by updating this study.
A study about COVID-19 is carried out in the present study and it is organized into four sections with section one as introductory in nature. Data and methodology have been discussed in the second section. In the third section, selected appropriate ARIMA model have illustrated using different statistical tools as well as appropriate graphs. Conclusions have been drawn on the basis of used analysis and reported in the fourth section.
Descriptions about data and methods have been discussed in this section.
4.1 Data
The data have been taken for the analysis are the number of new daily COVID-2019, total confirmed cases and new daily deceased cases from July 1, 2020 to August 3, 2021, and are extracted from the official website of the Indian Ministry of Health (https://api.COVID19india.org/). They include the overall national trend and all states of India. Some states of India have been reported more cases in comparison to other states. As is evident from the data, the state of Maharashtra is the worst affected in terms of total cases which accounts for about 23% of the cases in India. The next four worst affected states/ union territories are Tamil Nadu, Andhra Pradesh, Karnataka and Delhi having approximately 38% of the total cases and the rest of Indian states/ union territories having another 39% cases. Using appropriate ARIMA model, new daily confirmed cases, total confirmed cases and daily decease cases have been projected after August 3, 2021.
4.2 Methods
From the few months literature, it is observed that several studies have been conducted on COVID-19 and its projection in different places, of which some important contributors are Batista 202011-19 have been studied using different models and approaches. In this study, ARIMA model has been applied to know the pattern and as well as to forecast for future cases of COVID-19 (daily confirmed, total confirmed cases and daily deceases cases), as one of study has already reported that ARIMA is the good model to forecast time series data.12,15,16 It could be considered one of the good prediction models for time series.
The appropriate ARIMA(p, d, q) model parameters have been selected by using following criteria (i) the Akaike’s information criterion (AIC); (ii) autocorrelation function (ACF) and partial autocorrelation function (PACF) of the residuals; and (iii) testing the general statistical assumptions about residuals. Using above criteria, ARIMA (3,1,2), ARIMA (3,2,2) and ARIMA (0,1,2) have been applied to project daily confirmed cases, total confirmed cases and daily decease cases respectively.
In the first stage, Phillips–Perron Unit Root test (PP-test) for unit root as well as Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test have been applied to check the stationary time series data and then ACF and PACF plots of residuals as well as QQ-plots, histogram and other residuals plots are used to select the appropriate ARIMA model. Mean Error (ME), Mean absolute error (MSE), Mean Absolute Standard Error (MASE) and Autocorrelation function (ACF) have been calculated from forecast models to check the accuracy of the model and Durbin Watson test has also been applied to check autocorrelation disturbances among the residuals.
In this section, common statistical techniques related to ARIMA models have been discussed and importance of results has also been reported graphically. Present pattern of daily confirmed, total confirmed cases and daily deceased cases of COVID-19 are presented in the figure 1, 2 & 3, respectively.
From figure 1, it is observed that daily confirmed cases were increased in the month of August & September, 2020 and it was reported almost 100,000 cases in a day, and again cases were increased as second waive in the month of May& June, 2021 and it was reported more than 400,000 cases in a day. Similar interpretation can be seen in the figure 3 whereas figure 3 shows about daily deceased cases from July 1, 2020 to August 3, 2021.
Figure 2 indicates about total confirmed cases (from July 1, 2020 to August 3, 2021) and it can been seen from the figure that total confirmed cases have been increasing continuously although there is rapid outbreak of COVID19 cases in the month of September 2020 (reported more than 10,000,000 cases) as well as fast rapid outbreak May 2021(reported more than 30,000,000cases), It is observed that it has increased more than 3times within 7months.
5.1 Phillips–perron unit root and kpss test
The stationarity of the time series data can be checked with the help of Phillips–Perron (PP) Unit Root test, given in Paron.20 We used PP test to check about stationary and non-stationary time series and its results are given in Table 1. The p-value of the PP test is greater than the level of significance i.e., 0.05. Table 1 indicates that daily confirmed, total cases and daily deceased cases are non-stationary at 5% level of significance. It means all data (three cases) are required to transform into stationary time series data. Difference of series can be used to convert into stationary time series, where appropriate ARIMA models were selected with the help of minimum values of AIC, BIC and ME.
Variable |
Mean |
SD |
Min. |
Max. |
PP- test |
|
|
|
|
|
|
PP |
p-value |
Daily cases |
78150 |
90315.87 |
8579 |
414280 |
-2.598 |
0.951 |
Total cases |
13065966 |
9487445 |
605224 |
31767766 |
-0.581 |
0.99 |
Daily death |
1022 |
1122.62 |
75 |
6139 |
-14.19 |
0.315 |
Table 1 Summary statistics and PP-test for COVID-19 cases
The KPSS test can be applied to know nature of time series, whether it is stationary or not. This test is proposed by Kwiatkowski et al.21 The test p-value = 0.01, so we can assume that the series is not stationary. To check the stationarity of the series, we should have differences of the time series for the selection of appropriate model, difference of the series are required, It can be seen in the figure 7, where 1st, 2nd and1st differences have been required to convert into stationary for daily confirmed, total confirmed and daily deceased cases respectively.
5.2. ARIMA models and estimation of parameters
Appropriate ARIMA models have been selected using Akaike information criteria (AIC), Baysian information criteria (BIC), Mean absolute percentage error (MAPE) and Mean Error (ME) values of the parameters of model, which are presented in the table 1, 2 &3 respectively. Estimation of parameters of the selected models has been presented in the table 4. Accuracy of models have also been verified using ACF and PACF plots of residuals for daily confirmed , total confirmed and total deceased cases , which are presented in the figure 4,5 & 6 respectively. The absence of significance residuals spike indicates that almost all models are good fit. It can be seen from the figure 14, 15 &16 for daily confirmed, total confirmed and daily decease cases respectively, where QQ-plots, histogram and scatter plots of residuals are presented. Except some variation in normal plots, rest plots have been indicated good fits for the selected ARIMA models.
Cases |
KPSS level |
Lag parameter |
p-value |
Daily confirmed |
1.1224 |
5 |
0.01 |
Total confirmed |
5.8314 |
5 |
0.01 |
Daily deceased |
1.5355 |
5 |
0.01 |
Table 2 Summary of KPSS-test for COVID-19 cases
Cases |
Parameters |
AIC |
BIC |
MAPE |
ME |
Daily confirm |
(3,1,2) |
8245.01 |
8268.93 |
-0.32973 |
38.394 |
Total confirm |
(3,2,2) |
8225.06 |
8248.96 |
0.00711 |
33.2066 |
Daily Deceases |
(0,1,2) |
5774.28 |
5786.24 |
-3.62189 |
0.37571 |
Table 3 The optimal ARIMA models for different variables
Cases |
ARIMA |
Parameters |
|
|
|
||
|
Model |
|
|
|
|
|
|
|
|
AR1(S.E.) |
AR2(S.E.) |
AR3(S.E.) |
MA1(S.E.) |
MA2(S.E.) |
|
Daily confirm |
(3,1,2) |
0.0613(.05) |
-0.7671(.02) |
0.4068(.05) |
0.1465(.03) |
0.9397(.03) |
|
Total confirm |
(3,2,2) |
0.0626(.04) |
-0.7673(.03) |
0.4062 (.04) |
0.1438(.03) |
0.9420(.02) |
|
Daily Decease |
(0,1,2) |
- |
- |
- |
-0.6199(.05) |
0.0951(.05) |
|
Table 4 Estimation of parameters of ARIMA models for different variables
Cases |
Durbin Watson test |
Accuracy of forecast |
|
|
|
|
ME |
MASE |
ACF |
Daily confirmed |
1.98 |
-0.82801 |
0.6824 |
-0.06764 |
Total confirmed |
1.98 |
-1.47696 |
0.682913 |
-0.06631 |
Daily deceased |
2 |
-0.27882 |
0.861764 |
0.000392 |
Table 5 Durbin Watson Test and accuracy of forecast of models for three cases
Fitted and observed values for daily confirmed, total confirmed and daily decease cases are presented in figures 8,9 &10 respectively. From the figures, It is observed that very closed fit between observed and fitted values using ARIMA (3,1,2), ARIMA (3,2,2) and ARIMA (0,1,2) for daily confirmed, total confirmed and daily decease cases respectively.
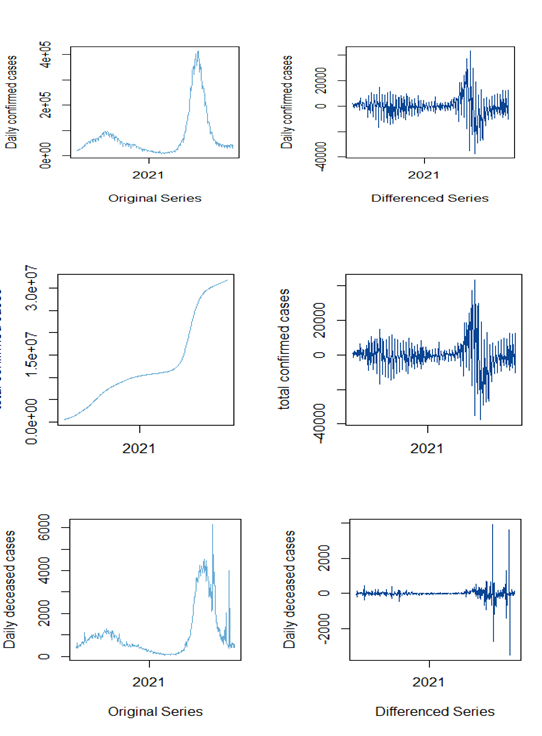
Figure 7 Plots of original and differences of daily confirmed, total confirmed, daily deceased cases respectively (from July, 2020, to August 3, 2021).
Figure 11 shows that forecast of ARIMA (3,1,2) for daily confirmed cases for next 120days (up to November 30, 2021), it is observed that daily cases are slightly decreasing with increased days. Point estimations and interval estimation (80% &95%) are calculated using optimum ARIMA model which indicates that there is no chances to increase daily confirm cases with increased days up to 512days which is up to November, 2021 as shown in the figure 11. Details about the forecast (point & Interval estimation) along with the date wise for next 120days (from August, 4 to November 30, 2021) are mentioned in the Appendix table 1. Its interval estimations are increasing with increased days and it is due to past two waives of COVID-19, where daily cases were found very high during second waives. On the basis of first waives of COVID-19 as well as point estimation of the model, there may be no chances to increase daily cases with increased number of days, if situation remains the same. As we see that different states and territories of governments of India are announcing to open colleges, schools and malls from August/ September, 2021, there may be less chance to increase the daily confirm cases during November/ December, 2021.
Figure 12 indicates the forcasst for total confirm cases for next 120days (from August 4 to November 30, 2021) using ARIMA (3,2,2) model. Total confirmed cases are slightly increasing with increased days as shown in the figure.Total confirm cases have been found incrasing pattern because daily confirm cases are adding. As per pattern of figure 12, total cases may be increased up to February/March, 2022. If the daily confirm cases does not increase, it will become stationary.
Figure 13 shows the forecast for daily decease cases for next 120 days (August 4 to November 30, 2021) using ARIMA (0,1,2) model. Daily deceases case shows slightly decreasing pattern up to Novmber, 2021 according to the model.
5.4 Accuracy of models and its forecasts
Accuracy of models can be checked using the plots of residuals and its normality test. It can be seen from the figure 14, 15 &16 respectively that the residual plots are normally distributed except with a little variation in QQ-plot. Durbin Watson test has also been applied to check its normality and autocorrelation of residuals for all three cases as well as accuracy of forecasting of models, which are presented in the table 5. If the value of autocorrelation is 2.00, it means there is no autocorrelation between residuals, if its value is less than 2 then positive autocorrelation and if it is more than 2 then negative autocorrelation between residuals using Durbin Watson. Mean Error (ME), Mean absolute standard error (MASE) and Auto correlation function (ACF) of error have been presented in table 5.
The authors are grateful to the chief editor as well anonymous referee for giving valuable comments to improve the quality of the paper.
Author declares there are no conflicts of interest.
None.

©2021 Shukla, et al. This is an open access article distributed under the terms of the, which permits unrestricted use, distribution, and build upon your work non-commercially.
2 7