A single-arm phase II clinical trial is usually conducted for finding an appropriate dose-level and testing toxicity for an experimental cancer therapy in comparison to some historical controls, and is usually the most doable trial type due to the feasibility under limited budget, patient pool and medical conditions that can be met. We considered the standard setting of a single-arm two-stage phase II clinical trial, and investigated the patterns of critical values and sample sizes at both two stages of minimax and optimal designs under different design parameters, i.e., under different response rates of control and treatment, significant level of the test, and statistical power. We provided analytic derivations to the patterns we are interested under large sample approximation, and investigated them under finite ans small sample via a numerical study by considering extensively possible design parameters over a fine grid. We finally concluded that the critical values at different stages of the test are related to the sample sizes at different stages in a similar way for both optimal and minimax designs, but they also reveal some differences and reflected the nature of these two types of design.

Keywords: single-arm two-stage trial, optimal design, minimax design, critical value, response rate

A phase II clinical trial is often conducted to find an appropriate dose-level and test toxicity for experimental cancer therapies in compare to some historical controls. This kind of trials usually requires small sample sizes due to ethical considerations, before proceeding to the subsequent phase of the trial for assessing the efficacy, outcomes and adverse effect in a larger group of subjects.^1,2 At the same time, a single-arm design is often the most doable trial due to the feasibility under limited budget, patient pool and medical conditions that can be met. The number of written requests reported on 2021 of single-arm trials issued by the Food and Drug Administration (FDA) of the United States is an essential volume.³

Statistically, the most simple and traditional single-arm phase II clinical trial design-the single-stage design, is specified as follows. Given the values of design parameters $({\alpha }^{*},1-{\beta }^{*},p_0,p_1)$ , that is, statistical significance level, power of the test, null response rate, and treatment response rate, respectively, we want to find a pair of positive integers $n,a$  to specify the sample size and rejection boundary (or critical value, for rejecting $H_0$ ) of the phase II trial under some constraints, and usually we also have a upper bound of $n$  specified subjectively, such as $25\sim 50$  to reflect the small-sample characteristic of a phase II trial.⁴ Then, starting from $n\ge n_0>0$  for a fixed $n_0$  (the minimal sample size needed), we can search over a grid the smallest integer $a$  such that based on level ${\alpha }^{*}$ , we reject $H_0$  if $X>a$  and otherwise fail to reject $H{}_0$ , that is, $\alpha =1-B_0(a;n)\le {\alpha }^{*}$  where $B_0(\cdot ;n)$  is the CDF of $Bin(n,p_0)$ . Then if the power $1-\beta =1-B_1(a,n)\ge 1-{\beta }^{\ast }$  where $B_1(\cdot ;n)$  is the CDF of $Bin(n,p_1)$ , the pair $n,a$  is said to be the optimal design. If there is no $a$  meet these conditions simultaneously, we continue to $n+1$ . Thus, the optimal design minimizes the sample size among all designs satisfies the conditions. It is also easy to know that the optimal single-stage design under a parameter setting is unique.

In some scenario, two-stage designs are more likely to be considered. In a two-stage design, the phase II clinical trial is conducted via two stages sequentially, and whether to proceed to the second stage depends on the results from the first stage. A desired design under the specifications of some parameters is given by finding appropriate sample sizes and critical values of the response rate of both two stages. The two-stage design is more economical and ethical, which makes the trial stop earlier if there is no efficacy tested, and the data collected is more informative than that from a single-stage trial if we proceed to phase III.⁴ Similar to single-stage design, the two-stage design is a mathematically easy problem since it can be done over a finite grid once the parameters are specified. In this paper, the problem is stated and discussed under the design of a single-arm two-stage phase II clinical trial.

The remainder of the paper is organized as follows. Section 4 reviewed the statistical setup of the single-arm two-stage phase II trials and described the scientific question of interest. We reviewed the classical optimal and minimax designs and discussed an issue we are concerned about involved in these two designs, and briefly stated our hunch. Section 5 introduced a numerical analysis to confirm our hunch. Section 6 concluded the paper.

Setup

Consider the test $H_0:p=p_0$  vs. $H_1:p=p_1$ , where $p_0$  is the response rate of a historical therapy, $p_1$  is the response rate of the experimental therapy needs to be tested, and under our context, $p_1=p_0+\delta$  for some $\delta >0$  as a clinical meaningful difference. We conduct the test by two stages. Denote $n=n_1+n_2$  with $n_j$  as the sample size of the test at stage $j(j=1,2)$ . Denote $X_1\sim Bin(n_1,p_i)$  and $X_2\sim Bin(n_2,p_i)$  under $H_i,i=0,1$ . $X_1$  and $X_2$  are independent.

We consider two types of stopping criteria when the phase II trial needs to be stopped after stage 1. First, we consider the futility (lower) stop only, which means we stop the trial after stage 1 only if we find the treatment is ineffective based on the result from stage 1, in other words, this happens when we find the positive response of stage 1 $x_1<a_1$  for a critical value $a_1$  that requires us to reject the null hypothesis $H_0$  under specified design parameters. Second, we consider both futility and superiority (upper) stops. The superiority stop means we also stop the trial when $x_1<b_1$  for a critical value $b_1$  that specifies the enough effectiveness of the treatment, i.e., because of the enough positive responses to the treatment, we can stop and claim the effectiveness of the treatment, and there is no need to conduct stage 2.

Specifically, the framework of finding specific designs of a single-arm two-stage phase II clinical trial is specified as follows. Under futility stop with design parameters $({\alpha }^{*},1-{\beta }^{*},p_0,p_1)$ :

1. Calculate $\alpha =P_0(X_1>a_1,X_1+X_2>a)$ , $1-\beta =P_1(X_1>a_1,X_1+X_2>a)$
2. Define probability of early termination (PET) under $H_0$ :$P_0(X_1\le a_1)$ and expected sample size (EN) under $H_0$ : $n_1\times PET+n\times (1-PET)$  

3. Among designs with $\alpha \le {\alpha }^{\ast }$ and $1-\beta \ge 1-{\beta }^{*}$ :

 - Optimal design $\left(a_1,n_1,a,n\right)$  minimizes EN

 - Minimax design $\left(a_1,n_1,a,n\right)$  minmizes $n=n_1+n_2$  

where $P_i$  is the probability measure under $H_i\left(i=0,1\right)$ . The significant level and power can be calculate by $P_i(X_1>a_1,X_1+X_2>a)={\displaystyle {\sum }_{x_{{}_1=a_1+1}}^{n_{{}_1}}{b}_i(x_1;n_1)\left\{1-B_i(a-x_1;n_2)\right\}}$  where $i=0$  for $\alpha$  and $i=1$  for $1-\beta$ , $b_i\left(\cdot ;n\right)$  is the probability mass of $Bin\left(n,p_i\right)$  and $B_i\left(\cdot ;n\right)$  is the corresponding CDF, $i=0,1$ . The algorithm of finding an optimal or minimax design is easy to implement via greedy searching over possible choices of $(n,n_1,a_1,a)$ . Starting from a $n\ge n_0$ , for $n_1\in \left[1,n-1\right],a_1\in \left[0,n_1\right],a\in \left[a_1+1,n\right]$ , the probabilities and EN aforementioned can be calculated, and so the corresponding designs can be found.

Under both futility and superiority stops with design parameters $({\alpha }^{*},1-{\beta }^{*},p_0,p_1)$ :

1. Calculate $1-\alpha =P_0(X_1\le a_1)+P_0(a_1<X_1<b_1,X_1+X_2\le a),\beta =P_1(X_1\le a_1)+P_1(a_1<X_1<b_1,X_1+X_2\le a)$
2. Define probability of early termination under   $H_i:PET(p_i)=P_i(X_1\le a_1)+P_i(X_1\ge b_1)$ , and expected sample size (EN) under $H_i:\text{EN}(p_i)=n_1\times \text{PET}(p_i)+n\times (1-\text{PET}(p_i))$ , $i=0,1$ , and then $\text{EN}=\frac{1}{2}[\text{EN}(p_0)+\text{EN}(p_1)]$  
3. Among designs with $\alpha \le {\alpha }^{*}$ and $1-\beta \ge 1-{\beta }^{*}$ :

 - Optimal design $(a_1,n_1,a,n)$  minimizes EN

 - Minimax design $(a_1,n_1,a,n)$  minmizes $n=n_1+n_2$  

A user-friendly software for finding optimal and minimax designs of two-stage phase II clinical trials can be found at http://www2.cscc.unc.edu/impact7/CTDSystems.

What are we looking for?

Following the notations in Section 4.1, we are interested if there is any pattern(s) among the $a_1,b_{1}a,n_1,n$  values we found from the desired designs given the constrains on level, power, etc. In fact, Jung⁴ found a phenomenon that $a\approx \frac{n}{2}(p_0+p_1)$ ,$a_1\approx n_1{p}_0$  and $b_1\approx n_1{p}_1$  by a few examples from the output of optimal and minimax trial designs, but has not investigated this in more details. We wanted to provide a formal analysis in the relationship of these numbers that an optimal or minimax design returns, given any specific setting of the design parameters, which we believe can provide some prior knowledge about what we can expect from a specific design, help us to understand more on the difference and similarity of minimax and optimal designs, and look at them from a new perspective.

First, we proved that under some regularity conditions and constraints by phase II clinical trials, and using large sample approximation, $\frac{a_1}{n_1}=p_0+O(n_1^{-1/2})$ , $\frac{b_1}{n_1}=p_1+O(n_1^{-1/2})$ , and $\frac{a}{n}=\lambda p_1+(1-\lambda )p_0+O(n^{-1/2})$  for some $\lambda \in [0,1]$ , and $\lambda$  is a parameter that can be related at least to the response rates of control and treatment, i.e., $p_0$  and $p_1$ . In other words, we may expect that the rejection criteria, i.e., the critical values $a_1,b_1$  and $a$  of the test are mainly determined by the response rates of control and treatment when the sample size is large. Details can be found in Appendix 7.1 for single-stage design and 7.2 for two-stage designs. Second, we used an extensive numerical study in Section 5 to confirm our hunch when the sample size is finite and small, and based on results from optimal and minimax designs.

Setup

We investigated the patterns of $a_1,b_1,a,n_1,n$  over a fine grid of parameters $(p_0,p_1,\alpha ,1-\beta )$ . We set $p_0$  ranged from $[0.05,0.7]$  with a small increment $5\times {10}^{-3}$ , and $p_1=p_0+\delta$ , where $\delta =0.2,0.25$ . We consider $\alpha \in \{0.05,0.1\}$  and $1-\beta \in \{0.8,0.85,0.9\}$  for all of these $p_0$  and $p_1$  values. We restricted the maximum of the total sample size $n$  by 55 to reflect the small-sample-size characteristic of phase II trials. Finally, we considered both optimal and minimax designs under two stop criteria, i.e., (1) with futility stop only; (2) with both futility and superiority stops.

Under a parameter setting, we searched the (minimax or optimal) design $(a_1,a,n_1,n)$  if the trial stops at futility stop of stage 1, $(a_1,b_1,a,n_1,n)$  if the trial is allowed to stop at both futility and superiority stops of stage 1.

Based on the theoretical results in Appendix 7, we investigated: (1) under futility stop only, the trends of $a_1/n_1-p_0$  (and $a_1-n_1{p}_0$ ) for stage 1, and $a/n-(p_0+p_1)/2$  (and $a-n(p_0+p_1)/2$ ) for stage 2, i.e. we choose $\lambda =1/2$  only in our numerical experiment (based on some previous experience and we would like to confirm how if $1/2$  is a good candidate for $\lambda$ ); (2) under both futility and superiority stops, the trends of $a_1/n_1-p_0$  (and $a_1-n_1{p}_0$ ) and $b_1/n_1-p_1$  (and $b_1-n_1{p}_1$ ) for stage 1, and $a/n-(p_0+p_1)/2$  (and $a-n(p_0+p_1)/2$ ) for stage 2.

Results

For simplicity and because of the similarity of our findings in multiple cases, we only present the results under $(\alpha ,1-\beta ,\delta )=(0.05,0.8,0.2)$ , where $\delta =p_1-p_0$ , as a representative, under both stop criteria and both designs. The complete results under all parameters we considered can be found in Appendix 8.

Figures 1& 2 show that for different $p_0$ , the trends of ratio differences we are interested, i.e., $a_1/n_1-p_0$ , $b_1/n_1-p_1$  and $a/n-\left(p_0+p_1\right)/2$ . They indicate that overall, these differences are close to 0, and the difference is smaller on stage 2, i.e., $a/n-\left(p_0+p_1\right)/2$ , under both stopping criteria, which means $\left(p_0+p_1\right)/2$  is a good approximation to $a/n$  over the $p_0$  we considered under this parameter setting. At the same time, we can observe that, the other two differences are also close to 0, but the differences under optimal design are overall closer to 0 than those of minimax design. The results for all other cases in Figure 3 to Figure 12 in Appendix 8.1 and 8.2 are similar to this case. We plotted all trends including differences in ratio and frequency. They also result in the same conclusion.

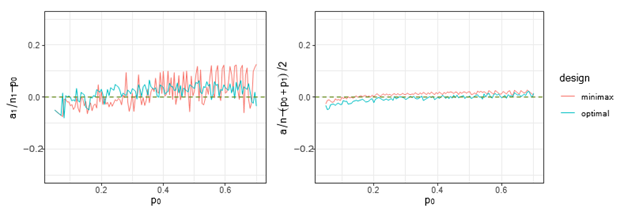
Figure 1 Trends of $a_1/n_1$  and $a/n$  under both optimal and minimax designs, when $({\alpha }^{*},1-{\beta }^{*},\delta )=(0.05,0.8,0.2)$  and there is futility stop only.

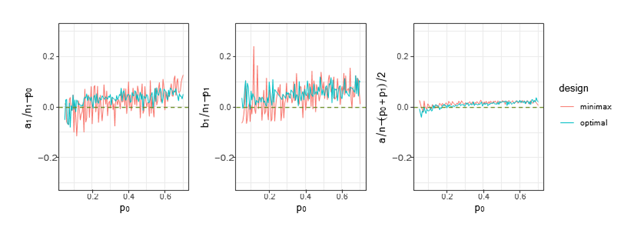
Figure 2 Trends of $a_1/n_1$ ,$b_1/n_1$ and $a/n$ under both optimal and minimax designs, when $({\alpha }^{*},1-{\beta }^{*},\delta )=(0.05,0.8,0.2)$ and there are both futility and superiority stops.

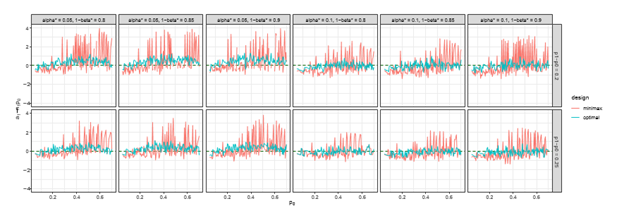
Figure 3 The trends of $a_1-n_1{p}_0$ over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there is futility stop only.

Table 1 calculates the summary statistics of the trends in Figures 1 &2 over different $p_0$  (in total, there are 131 $p_0$ ’s in each figure). We found from the mean that, these differences are very close to 0 on average, and thus the approximation we use is good. We found from the interquartile range (IQR) and standard deviation (SD) that they are larger for minimax design than optimal design for a same difference, thus the variation of the approximation on optimal design is smaller. Table 2 further provides all numerical results under this setting, i.e. $({\alpha }^{*},1-{\beta }^{*},\delta )=(0.05,0.8,0.2)$ , including all design outputs, ratios and differences of interest. We present results over $p_0\in [0.05,0.7]$  but with increment $5\times {10}^{-2}$  compared to $5\times {10}^{-3}$  for the figures in order to maintain the concision and information provided by the table.

In this paper, we focused on single-arm two-stage phase II clinical trials, which is widely needed in reality. We specifically take the trends of critical values for rejecting null hypothesis at both two stages in a phase II clinical trial into consideration. Using both theoretical derivations under large-sample and numerical studies under finite and small sample, we confirmed that the critical values can be approximated and dominated by the total sample sizes and response rates of different stages. We also found that, this approximation is more obvious in optimal design than that in minimax design under the same design parameter setting. Our finding indicates that although minimax design provides less total sample size needed for a phase II trial, the property of an optimal design is closer to what we expect under large sample, and overall the optimal designs have more stable patterns on their relationships among critical values, sample sizes of both stages and response rates under null and alternative hypotheses.

The numerical study in Section 5 confirms our hunch in Section 4.2 under finite (and actually small) sample. In this section, we provide some analytic proofs about the relationship between $n_1,a_1,b_1,n,a,p_0$  and $p_1$  when the total sample size $n$  is large, using normal approximation, based on some regular assumptions (specified later).

Large sample approximation of single-stage phase II trials

In a single-arm single-stage trial, given a large $n$ , we can find the approximate value of $a$  using large sample approximation. We assume that there exist $\epsilon$  and $\delta >0$  such that $0<\epsilon \le p_0<p_1=p_0+\delta \le 1-\epsilon <1$ , which means the response rates satisfy the “positivity”, i.e., bounded away from 0 and 1. In reality, this means we assume that a treatment cannot be effective or ineffective to all subjects in the target population. Next, denote $\overline{X}=X/n$ , then under $H_i (i=0,1)$ :

$\sqrt{n}(\overline{X}-p_i)\stackrel{d}{\to }N(0,p_i{q}_i)$   (7.1.1)

as $n\to \infty$ , where $q_i=1-p_i$ , $i=0,1$ . Denote $P(\cdot |p=p_i)$  by $P_i(\cdot ), i=0,1$ . Given $({\alpha }^{*},1-{\beta }^{*})$ , $n$  and $a$  satisfy ${\alpha }^{*}=P_0(X>a)$  and $1-{\beta }^{*}=P_1(X>a)$ . So, under a large sample,

$a/n=p_0+z_{1-{\alpha }^{*}}\sqrt{p_0{q}_0/n}$    (7.1.2)

 and

$a/n=p_1-z_{1-{\beta }^{*}}\sqrt{p_1{q}_1/n}$   (7.1.3)

where $z_{\gamma }$  is the $\gamma$ -quantile of the standard normal distribution. From (7.1.2) and (7.1.3), we know

$p_1=p_0+\delta p_0+z_{1-{\alpha }^{*}}\sqrt{p_0{q}_0/n}=p_1-z_{1-{\beta }^{*}}\sqrt{p_1{q}_1/n}$

or

$\sqrt{n}=\frac{z_{1-{\alpha }^{*}}\sqrt{p_0{q}_0}+z_{1-{\beta }^{*}}\sqrt{p_1{q}_1}}{p_1-p_0}$

By plugging this in (7.1.2) or (7.1.3), we have

$\frac{a}{n}=\lambda p_0+(1-\lambda )p_1$   (7.1.4)

with   $\lambda =\frac{z_{1-{\beta }^{*}}\sqrt{p_1{q}_1}}{z_{1-{\alpha }^{*}}\sqrt{p_0{q}_0}+z_{1-{\beta }^{*}}\sqrt{p_1{q}_1}}\$$ .

Note that both $z_{1-{\alpha }^{*}}$  and $z_{1-{\beta }^{*}}$  are finite, and usually, in phase II clinical trials, we choose ${\alpha }^{*}<{\beta }^{*}$  so that $z_{1-{\alpha }^{*}}>z_{1-{\beta }^{*}}$ . Hence, if $p_0{q}_0<p_1{q}_1$ , the weights in (7.1.4) are closer to $1/2$ .

Large sample approximation of two-stage phase II trials

In the case of two-stage trials, we investigated in Section 5 by numerical studies under finite and small sample. Now, we provide an analytic proof assuming some regularity conditions about  under large sample. Following notations in Section 4.1, note that under $H_i (i=0,1)$ :

$\sqrt{n_j}({\overline{X}}_j-p_i)\stackrel{d}{\to }N(0,p_i{q}_i)$   (7.2.1)

as $n_j\to \infty$ , where $q_i=1-p_i, {\overline{X}}_j=X_j/n_j, j=1,2$ .

Under futility stop only

Under a large $n=n_1+n_2$  and assume $n_1/n\to r\in (0,1)$ , a constant, as $n\to \infty$ , the condition $P_0(X_1>a_1,X_1+X_2>a)={\alpha }^{*}$  is equivalent to

${\alpha }^{*}={\displaystyle {\int }_{a_1/n_1}^{\infty }{S}_{0;{\overline{X}}_2}}\left(\frac{n_1}{n_2}\left[\frac{a}{n_1}-{\overline{x}}_1\right]\right)f_{0;{\overline{X}}_1}({\overline{x}}_1)d\overline{x}$ ,

where $f_{0;{\overline{X}}_1}$  is the density of ${\overline{X}}_1$ , and $S_{0;{\overline{X}}_2}$  is the survival function of ${\overline{X}}_2$  under $H_0$ . Note that

$S_{0;{\overline{X}}_2}\left(\frac{n_1}{n_2}\left[\frac{a}{n_1}-{\overline{x}}_1\right]\right)=1-\Phi \left(\frac{n_1{n}_2^{-1}(a/n_1-{\overline{x}}_1)-p_0}{\sqrt{p_0{q}_0/n_2}}\right)$

where $\Phi$  is the CDF of a standard normal distribution. Let

$\tau ={\displaystyle {\int }_{a_1/n_1}^{\infty }\Phi }\left(\frac{n_1{n}_2^{-1}(a/n_1-{\overline{x}}_1)-p_0}{\sqrt{p_0{q}_0/n_2}}\right)f_{0;{\overline{X}}_1}({\overline{x}}_1)d{\overline{x}}_1$ ,

Note that there exists an $\epsilon >0$  such that $0<\epsilon \le \tau \le 1-\epsilon <1$  since the lower limit of the above integral $a_1/n_1>0$ .

Then,

$P_0(X_1>a_1)={\displaystyle {\int }_{a_1/n_1}^{\infty }{f}_{0;{\overline{X}}_1}}({\overline{x}}_1)d{\overline{x}}_1=\tau +{\alpha }^{*}$   (7.2.2)

Therefore, by (7.2.1) and (7.2.2), we know

$\frac{a_1}{n_1}=p_0+z_{1-\tau -{\alpha }^{*}}\sqrt{p_0{q}_0/n_1}$    (7.2.3)

where $z_{\gamma }$  is the $\gamma$ -quantile of the standard normal distribution. Thus, if we choose ${\alpha }^{*}\le 1-\tau$  (achievable usually since ${\alpha }^{*}$  should be small in practice), then $z_{1-\tau -{\alpha }^{*}}$  is finite, and thus $\frac{a_1}{n_1}\approx p_0$  as $n\to \infty$ .

Next, we show the relationship among $a,n,p_0$  and $p_1$ . Let $X=X_1+X_2$  and by independence, $X~Bin(n,p_i)$  under $H_i (i=0,1)$ . Thus, (7.1.1) holds for $\overline{X}=X/n$ . We know $P_0(X_1>a_1,X>a)={\alpha }^{*}$  and $P_1(X_1>a_1,X>a)=1-{\beta }^{*}$ .

One the one hand, $P_1(X>a)=1-{\beta }^{*}+P_1(X>a,X_1\le a_1)$ , and let

${\tau }_1=P_1(X>a,X_1\le a_1)={\displaystyle {\int }_0^{a_1/n_1}{S}_{1;{\overline{X}}_2}}\left(\frac{n_1}{n_2}\left[\frac{a}{n_1}-{\overline{x}}_1\right]\right)f_{1;{\overline{X}}_1}({\overline{x}}_1)d{\overline{x}}_1$

${\tau }_1=P_1(X>a,X_1\le a_1)={\displaystyle {\int }_0^{a_1/n_1}{S}_{1;{\overline{X}}_2}}\left(\frac{n_1}{n_2}\left[\frac{a}{n_1}-{\overline{x}}_1\right]\right)f_{1;{\overline{X}}_1}({\overline{x}}_1)d{\overline{x}}_1$

On the other hand, $P_0(X>a)={\alpha }^{*}+P_0(X>a,X_1\le a_1)$  and let

${\tau }_0=P_0(X>a,X_1\le a_1)={\displaystyle {\int }_0^{a_1/n_1}{S}_{0;{\overline{X}}_2}}\left(\frac{n_1}{n_2}\left[\frac{a}{n_1}-{\overline{x}}_1\right]\right)f_{0;{\overline{X}}_1}({\overline{x}}_1)d{\overline{x}}_1$

$\le S_{0;{\overline{X}}_2}\left(\frac{a}{n_2}\right){\displaystyle {\int }_0^{a_1/n_1}{f}_{0;{\overline{X}}_1}}({\overline{x}}_1)d{\overline{x}}_1$

We note that there exist an $\epsilon >0$  such that $S_{i;{\overline{X}}_2}\left(\frac{a}{n_2}\right)\le 1-\epsilon <1$  for both $i=0,1$ , thus the right hand side of the above two probabilities are conservatively equal to $1-\epsilon$  under large sample. Now,

$a/n=p_0+z_{1-{\alpha }^{*}-{\tau }_0}\sqrt{p_0{q}_0/n}=p_1-z_{1-{\beta }^{*}+{\tau }_1}\sqrt{p_1{q}_1/n}$

Thus,

$\frac{a}{n}=\lambda p_1+(1-\lambda )p_0$   (7.2.4)

with $\lambda =\frac{z_{1-{\alpha }^{*}-{\tau }_0}\sqrt{p_0{q}_0}}{z_{1-{\alpha }^{*}-{\tau }_0}\sqrt{p_0{q}_0}+z_{1-{\beta }^{*}+{\tau }_1}\sqrt{p_1{q}_1}}$ . By choosing ${\alpha }^{*},1-{\beta }^{*}<\epsilon$ , we have ${\tau }_0<1-{\alpha }^{*}$  and ${\tau }_1<{\beta }^{*}$ , so both $z_{1-{\alpha }^{*}-{\tau }_0}$  and $z_{1-{\beta }^{*}+{\tau }_1}$  are finite. Whether the weights in (7.2.4) are closer to 1/2 is a more complicated problem here than that in Section 7.1.

Under both futility and superiority stops

Following the same notations and assumptions made in Section 7.2.1, note that similar to the thoughts in Section 7.2.1, condition $1-{\alpha }^{*}=P_0(X_1\le a_1)+P_0(a_1<X_1<b_1,X_1+X_2\le a)$  is equivalent to

$P_0(X_1>a_1)={\displaystyle {\int }_{a_1/n_1}^{\infty }{f}_{0;{\overline{X}}_1}}({\overline{x}}_1)d{\overline{x}}_1=\tau +{\alpha }^{*}$

where

$\tau ={\displaystyle {\int }_{a_1/n_1}^{b_1/n_1}{S}_{0;{\overline{X}}_2}}\left(\frac{n_1}{n_2}\left[\frac{a}{n_1}-{\overline{x}}_1\right]\right)f_{0;{\overline{X}}_1}({\overline{x}}_1)d{\overline{x}}_1$

Thus, by choosing ${\alpha }^{*}<1-\tau$ , we can similarly show that

$\frac{a_1}{n_1}=p_0+z_{1-{\alpha }^{*}-\tau }\sqrt{p_0{q}_0/n_1}$   (7.2.5)

 Thus, $\frac{a_1}{n_1}\approx p_0$ .

Second, we note that $P_1(X_1\le a_1)+P_1(a_1<X_1<b_1,X\le a)=P_1(X_1\le a_1,X\le a)+P_1(X_1\le a_1,X>a)+P_1(a_1<X_1<b_1,X\le a)=P_1(X_1<b_1,X\le a)+P_1(X_1\le a_1,X>a)=P_1(X_1<b_1)-P_1(X_1<b_1,X>a)+P_1(X_1\le a_1,X>a)$ . Hence, the condition ${\beta }^{*}=P_1(X_1\le a_1)+P_1(a_1<X_1<b_1,X_1+X_2\le a)$  is equivalent to $P_1(X_1<b_1)-P_1(a_1<X_1<b_1,X>a)={\beta }^{*}$ , thus

$P_1(X_1>b_1)={\displaystyle {\int }_{b_1/n_1}^{\infty }{f}_{1;{\overline{X}}_1}}({\overline{x}}_1)d{\overline{x}}_1=1-{\beta }^{*}+\tau$

where

$\tau ={\displaystyle {\int }_{a_1/n_1}^{b_1/n_1}{S}_{1;{\overline{X}}_2}}\left(\frac{n_1}{n_2}\left[\frac{a}{n_1}-{\overline{x}}_1\right]\right)f_{1;{\overline{X}}_1}({\overline{x}}_1)d{\overline{x}}_1$

Then, by choosing ${\beta }^{*}>\tau$ , we know that

$\frac{b_1}{n_1}=p_1-z_{(1-{\beta }^{*}+\tau )}\sqrt{p_1{q}_1/n_1}$   (7.2.6)

 Thus, $\frac{b_1}{n_1}\approx p_1$ .

Finally, denote $X=X_1+X_2$ , and we have that ${\beta }^{*}=P_1(X_1\le a_1)+P_1(a_1<X_1<b_1,X\le a)$ ,

and $1-{\alpha }^{*}=P_0(X_1\le a_1)+P_0(a_1<X_1<b_1,X\le a)$ . Let

${\tau }_0=P_0(a_1<X_1<b_1,X\le a)={\displaystyle {\int }_{a_1/n_1}^{b_1/n_1}\Phi }\left(\frac{n_1{n}_2^{-1}(a/n_1-{\overline{x}}_1)-p_0}{\sqrt{p_0{q}_0/n_2}}\right)f_{0;{\overline{X}}_1}({\overline{x}}_1)d{\overline{x}}_1$

and

${\tau }_1=P_1(a_1<X_1<b_1,X\le a)={\displaystyle {\int }_{a_1/n_1}^{b_1/n_1}\Phi }\left(\frac{n_1{n}_2^{-1}(a/n_1-{\overline{x}}_1)-p_1}{\sqrt{p_1{q}_1/n_2}}\right)f_{1;{\overline{X}}_1}({\overline{x}}_1)d{\overline{x}}_1$

where $\Phi$  is the CDF of the standard normal distribution, and thus choosing ${\alpha }^{*}<1-{\tau }_0$  and ${\beta }^{*}>{\tau }_1$ , similar to the proof in Section 7.2.1, we have

$\frac{a}{n}=\lambda p_0+(1-\lambda )p_1$   (7.2.7)

where $\lambda =\frac{z_{1-{\alpha }^{*}-{\tau }_0}\sqrt{p_0{q}_0}}{z_{1-{\alpha }^{*}-{\tau }_0}\sqrt{p_0{q}_0}+z_{1-{\beta }^{*}+{\tau }_1}\sqrt{p_1{q}_1}}$ .

We provide figures of two types of trends. That is, trends in frequency (Figures 3 & 4) for investigating the trends of  and , and trends in difference of ratio (Figures 5 & 6) for investigating the trends of $a_1/n_1$  and $a/n$ .

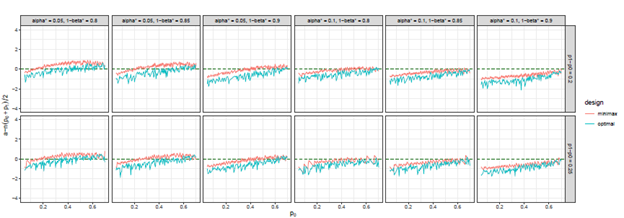
Figure 4 The trends of $a-n\left(p_0+p_1\right)/2$ over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there is futility stop only.

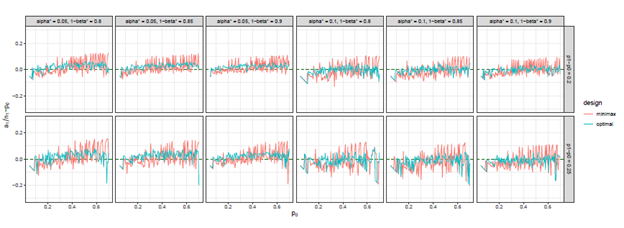
Figure 5 The trends of $a_1/n_1-p_0$ (ratio) over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there is futility stop only.

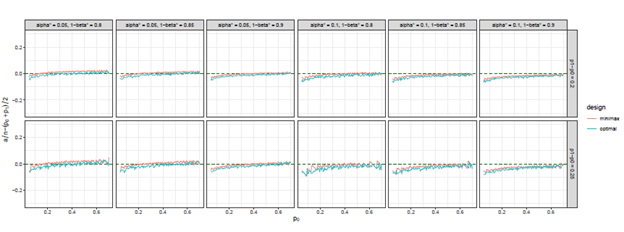
Figure 6 The trends of $a-n\left(p_0+p_1\right)/2$ (ratio) over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there is futility stop only.

Table 3– Table 8 present all numerical results, including the returns of designs, ratios, and differences of interest under all parameter settings in this numerical study. Specifically, we only present under $p_0\in \left[0.05,0.7\right]$  with an increment $5\times {10}^{-2}$  compared to $5\times {10}^{-3}$  in the figures, for maintaining the information and concision provided by the tables simultaneously. Each table represents a case of $\left({\alpha }^{\ast },1-{\beta }^{\ast }\right)$ .

Results under both futility and superiority stops

Same as Section 8.1, we provide figures of trends in frequency (Figure 7-Figure 9) for investigating the trends of $a_1$ , $b_1$  and $a$ , and trends in difference of ratio (Figure 10-Figure 12) for investigating the trends of $a_1/n_1$ , $b_1/n_1$  and $a/n$ .

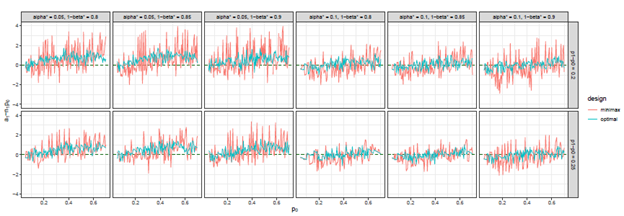
Figure 7 The trends of $a_1-n_1{p}_0$ over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there are both futility and superiority stops.

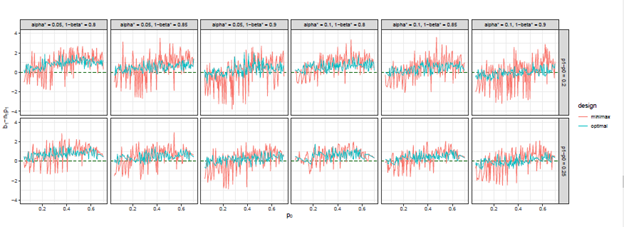
Figure 8 The trends of $b_1/n_1{p}_1$ over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there are both futility and superiority stops.

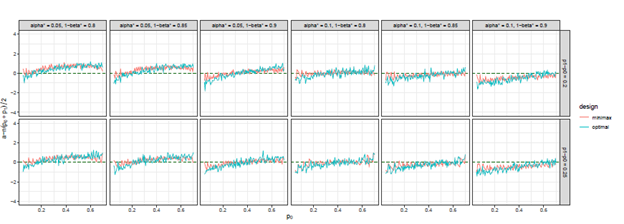
Figure 9 The trends of $a-n\left(p_0+p_1\right)/2$ over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there are both futility and superiority stops.

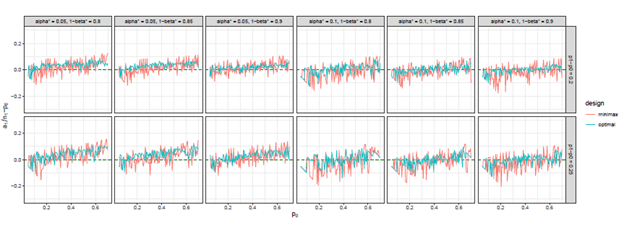
Figure 10 The trends of $a_1/n_1-p_0$ (ratio) over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there are both futility and superiority stops.

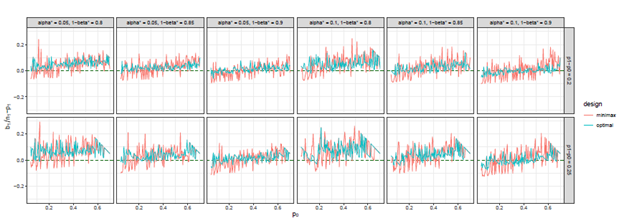
Figure 11 The trends of $b_1/n_1-p_1$ over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there are both futility and superiority stops.

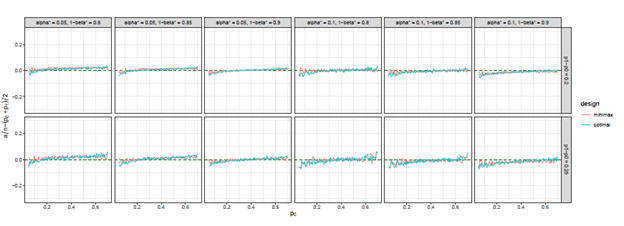
Figure 12 The trends of $a-n\left(p_0+p_1\right)/2$ (ratio) over different choices of ${\alpha }^{*},1-{\beta }^{*},\delta =p_1-p_0$ , under both optimal and minimax designs, when there are both futility and superiority stops.

Table 9-Table 14 present all numerical results, including the returns of designs, ratios, and differences of interest under all parameter settings in this numerical study. Specifically, we only present under $p_0\in \left[0.05,0.7\right]$  with an increment $5\times {10}^{-2}$  compared to $5\times {10}^{-3}$  in the figures, for maintaining the information and concision provided by the tables simultaneously. Each table represents a case of ${\alpha }^{\ast },1-{\beta }^{\ast }$ .

None.

The authors declared that there are no conflicts of interest.

1. Gail AVan Norman. Phase II trials in drug development and adaptive trial design. JACC: Basic to Translational Science. 2019;4(3):428–437.
2. Lu Liu, Shiwei Cao, Sin Ho Jung. Optimal designs for phase ii clinical trials with heterogeneous patient populations. J Biopharm Stat. 2022;1–14.
3. Ziyu Ji, Junjing Lin, Jianchang Lin. Optimal sample size determination for single-arm trials in pediatric and rare populations with bayesian borrowing. J Biopharm Stat. 2022;32(4):529–546.
4. Sin Ho Jung. Randomized phase II cancer clinical trials. CRC Press:2013.