In the present paper, a new one parameter lifetime distribution named, “Adya distribution’ has been proposed for modeling lifetime data from engineering. Its various statistical properties including moments and moments based measures, hazard rate function, mean residual life function, stochastic ordering, deviations from the mean and the median, Bonferroni and Lorenz curves, and stress-strength reliability have been studied. Both the method of moment and the maximum likelihood estimation have been discussed for estimating the parameter of the proposed distribution. A numerical example has been presented to test the goodness of fit of the proposed distribution over other one parameter lifetime distributions available in statistical literature.

Keywords: lifetime distributions, statistical and mathematical properties, parameter estimation, goodness of fit

The classical one parameter exponential distribution and Lindley distribution proposed by Lindley¹ were useful for modeling lifetime data from engineering and biomedical. It has been observed by Shanker et al.² that exponential and Lindley distributions are not suitable for several lifetime data. In search for better one parameter lifetime distributions, Shanker has introduced several one parameter lifetime distributions including Shanker,³ Aradhana,⁴ Sujatha,⁵ Devya.⁶ The probability density function (pdf) and the cumulative distribution function (cdf) of these distributions are presented in table 1.

The reasons for introducing such lifetime distributions with their advantages and disadvantages, statistical properties, parameter estimation and applications are available in the respective papers.

In this paper, a new lifetime distribution which gives better fit over several one parameter lifetime distributions are introduced. The new one parameter lifetime distribution is defined by its cdf and pdf, respectively

$F\left(x,\theta \right)=1-\left[1+\frac{\theta x\left(\theta x+2{\theta }^2+2\right)}{{\theta }^4+2{\theta }^2+2}\right]e^{-\theta x};x>0,\theta >0$ (1.1)

$f\left(x;\theta \right)=\frac{{\theta }^3}{{\theta }^4+2{\theta }^2+2}{\left(\theta +x\right)}^2{e}^{-\theta x};x>0,\theta >0$ (1.2)

 We name this distribution, “Adya distribution”. This is a convex combination of exponential $\left(\theta \right)$ , gamma $\left(2,\theta \right)$ and gamma $\left(3,\theta \right)$ distributions. We have

 Where $p_1=\frac{{\theta }^4}{{\theta }^4+2{\theta }^2+2}$ ,$p_2=\frac{2{\theta }^4}{{\theta }^4+2{\theta }^2+2}$ ,$g_1\left(x;\theta \right)=\theta e^{-\theta x}$ ,$g_2\left(x;2,\theta \right)=\frac{{\theta }^2}{\Gamma \left(2\right)}{x}^{2-1}{e}^{-\theta x}$ , and $g_3\left(x;3,\theta \right)=\frac{{\theta }^3}{\Gamma \left(3\right)}{x}^{3-1}{e}^{-\theta x}$ ;$;x>0,\theta >0$ .

The pdf and the cdf of Adya distribution for values of the parameter $\theta$ are shown in figures 1 and 2, respectively.

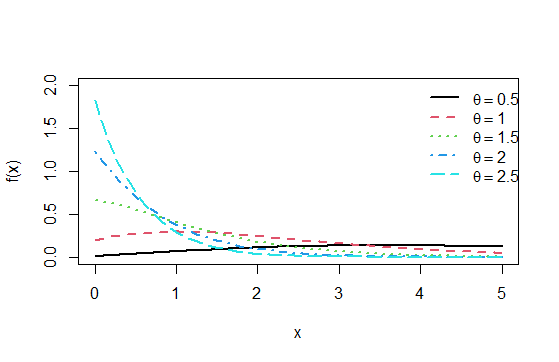
Figure 1 The pdf of Adya distribution .

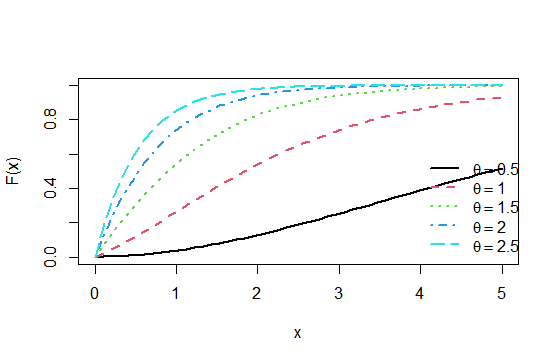
Figure 2 The cdf of Adya distribution .

The $r$ th moment about origin ${\mu }_r{}^{\prime }$ of (1.2) can be obtained as

${\mu }_r{}^{\prime }=\frac{r!\left\{{\theta }^4+2\left(r+1\right){\theta }^2+\left(r+1\right)\left(r+2\right)\right\}}{{\theta }^r\left({\theta }^4+2{\theta }^2+2\right)};r=1,2,3,\mathrm{...}$ (2.1)

Substituting$r=1,2,3,\text{and}4$ in (2.1), the first four moments about origin of (1.2) are obtained as

${\mu }_1{}^{\prime }=\frac{{\theta }^4+4{\theta }^2+6}{\theta \left({\theta }^4+2{\theta }^2+2\right)}$ ,${\mu }_2{}^{\prime }=\frac{2\left({\theta }^4+6{\theta }^2+12\right)}{{\theta }^2\left({\theta }^4+2{\theta }^2+2\right)}$ ,

${\mu }_3{}^{\prime }=\frac{6\left({\theta }^4+8{\theta }^2+20\right)}{{\theta }^3\left({\theta }^4+2{\theta }^2+2\right)}$ ,${\mu }_4{}^{\prime }=\frac{24\left({\theta }^4+10{\theta }^2+30\right)}{{\theta }^4\left({\theta }^4+2{\theta }^2+2\right)}$

Thus, the central moments of (1.2) are obtained as

Descriptive measures including coefficient of variation $\left(C.V\right)$ , coefficient of skweness $\left(\sqrt{{\beta }_1}\right)$ , coefficient of kurtosis $\left({\beta }_2\right)$ and index of dispersion $\left(\gamma \right)$ of (1.2) are thus obtained as

The natures of these descriptive measures for values of parameter  are shown in figure 3.

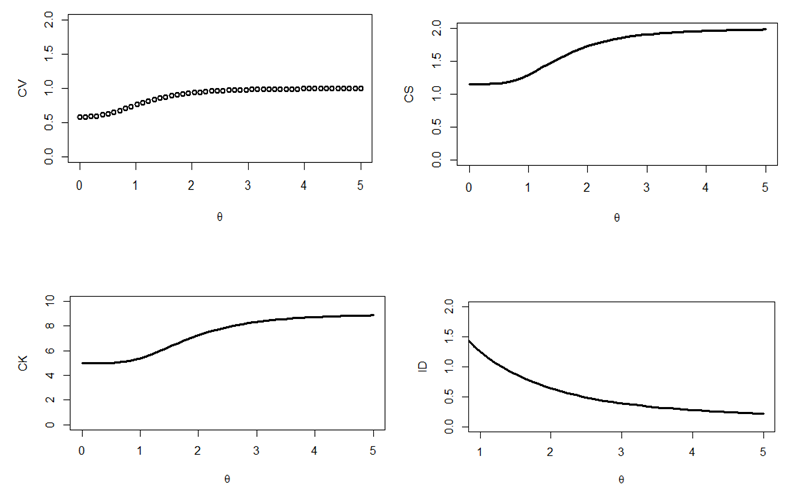
Figure 3 Coefficients of variation, skewness, kurtosis and index of dispersion of Adya distribution .

The condition under which Adya distribution is over-dispersed, equi-dispersed, and under-dispersed along with condition under which Shanker, Aradhana, Sujatha, Devya, Lindley and exponential distributions are over-dispersed, equi-dispersed, and under-dispersed are presented in table 2.

The hazard rate function and the mean residual life function of a continuous random variable$X$ having pdf and cdf $f\left(x\right)$ and $F\left(x\right)$ are, respectively, defined as

$h\left(x\right)=\underset{\Delta x\to 0}{\lim }\frac{P\left(X<x+\Delta x|X>x\right)}{\Delta x}=\frac{f\left(x\right)}{1-F\left(x\right)}$ (3.1)

and$m\left(x\right)=E\left[X-x|X>x\right]=\frac{1}{1-F\left(x\right)}{\displaystyle {\int }_x^{\infty }\left[1-F\left(t\right)\right]}dt$ (3.2)

Thus,$h\left(x\right)$ and $m\left(x\right)$ of (1.2) are obtained as

$h\left(x\right)=\frac{{\theta }^3{\left(\theta +x\right)}^2}{{\theta }^2{x}^2+2\theta \left({\theta }^2+1\right)x+\left({\theta }^4+2{\theta }^2+2\right)}$ (3.3)

 and

$=\frac{{\theta }^2{x}^2+2\theta \left({\theta }^2+2\right)x+\left({\theta }^4+4{\theta }^2+6\right)}{\theta \left[{\theta }^2{x}^2+2\theta \left({\theta }^2+1\right)x+\left({\theta }^4+2{\theta }^2+2\right)\right]}$ (3.4)

This gives$h\left(0\right)=\frac{{\theta }^5}{{\theta }^4+2{\theta }^2+2}=f\left(0\right)$ and $m\left(0\right)=\frac{{\theta }^4+4{\theta }^2+6}{\theta \left({\theta }^4+2{\theta }^2+2\right)}={\mu }_1{}^{\prime }$ . The hazard rate function and mean residual life function of Adya distribution are shown in figure 4.

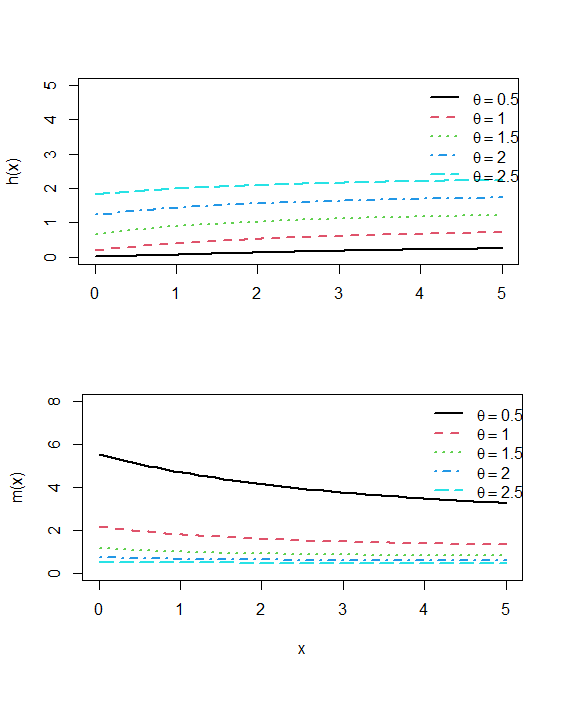
Figure 4 Graphs of $h\left(x\right)$ and $m\left(x\right)$ of Adya distribution .

A random variable $X$ is said to be smaller than a random variable in the

1. stochastic order $\left(X{\le }_{st}Y\right)$ if $F_X\left(x\right)\ge F_Y\left(x\right)$ for all $x$
2. hazard rate order $\left(X{\le }_{hr}Y\right)$ if $h_X\left(x\right)\ge h_Y\left(x\right)$ for all$x$
3. mean residual life order $\left(X{\le }_{mrl}Y\right)$ if $m_X\left(x\right)\le m_Y\left(x\right)$ for all $x$
4. likelihood ratio order $\left(X{\le }_{lr}Y\right)$ if $\frac{f_X\left(x\right)}{f_Y\left(x\right)}$ decreases in$x$

Shaked and Shanthikumar⁷ proposed following results for establishing stochastic ordering of distributions

$X{\le }_{lr}Y\Rightarrow X{\le }_{hr}Y\Rightarrow X{\le }_{mrl}Y$ (4.1)

The distribution (1.2) is ordered with respect to the strongest ‘likelihood ratio’ ordering.

Theorem: Suppose $X$ $\sim$ Adya distributon $\left({\theta }_1\right)$ and $Y$ $\sim$ Adya distribution $\left({\theta }_2\right)$ . If ${\theta }_1>{\theta }_2$ , then $X{\le }_{lr}Y$ and hence $X{\le }_{hr}Y$ ,$X{\le }_{mrl}Y$ and $X{\le }_{st}Y$ .

Proof: We have

  Now

 .

 This gives$\frac{d}{dx}\left\{\ln \frac{f_X\left(x\right)}{f_Y\left(x\right)}\right\}=\frac{-2\left({\theta }_1-{\theta }_2\right)}{\left({\theta }_1+x\right)\left({\theta }_2+x\right)}-\left({\theta }_1-{\theta }_2\right)$

 Thus for${\theta }_1>{\theta }_2$ ,$\frac{d}{dx}\left\{\ln \frac{f_X\left(x\right)}{f_Y\left(x\right)}\right\}<0$ . This means that $X{\le }_{lr}Y$ and hence $X{\le }_{hr}Y$ ,$X{\le }_{mrl}Y$ and $X{\le }_{st}Y$ .

The mean deviation about the mean and the mean deviation about the median are used to measure the amount of scatter in the population from the mean and the median and defined by

${\delta }_1\left(X\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}\left|x-\mu \right|}f\left(x\right)dx$ and ${\delta }_2\left(X\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}\left|x-M\right|}f\left(x\right)dx$ , respectively, where $\mu =E\left(X\right)$ and $M=\text{Median }\left(X\right)$ . The computation of these measures are simplified as

${\delta }_1\left(X\right)={\displaystyle \underset{0}{\overset{\mu }{\int }}\left(\mu -x\right)}f\left(x\right)dx+{\displaystyle \underset{\mu }{\overset{\infty }{\int }}\left(x-\mu \right)}f\left(x\right)dx=2\mu F\left(\mu \right)-2{\displaystyle \underset{0}{\overset{\mu }{\int }}x}f\left(x\right)dx$ (5.1)

and

${\delta }_2\left(X\right)={\displaystyle \underset{0}{\overset{M}{\int }}\left(M-x\right)}f\left(x\right)dx+{\displaystyle \underset{M}{\overset{\infty }{\int }}\left(x-M\right)}f\left(x\right)dx=\mu -2{\displaystyle \underset{0}{\overset{M}{\int }}x}f\left(x\right)dx$ (5.2)

Using pdf (1.2) and expression for the mean of Adya distribution ,we get

${\displaystyle \underset{0}{\overset{\mu }{\int }}x}f\left(x;\theta \right)dx=\mu -\frac{\left\{{\theta }^5\mu +{\theta }^4\left(2{\mu }^2+1\right)+{\theta }^3({\mu }^3+4\mu )+{\theta }^2(3{\mu }^2+\mu )+6\theta \mu +6\right\}{e}^{-\theta \mu }}{\theta \left({\theta }^4+2{\theta }^2+2\right)}$ (5.3)

${\displaystyle \underset{0}{\overset{M}{\int }}x}f\left(x;\theta \right)dx=\mu -\frac{\left\{{\theta }^{5}M+{\theta }^4(2M^2+1)+{\theta }^3(M^3+4M)+{\theta }^2(3M^2+M)+6\theta M+6\right\}{e}^{-\theta M}}{\theta \left({\theta }^4+2{\theta }^2+2)\right)}$ (5.4)

Using expressions from (5.1), (5.2), (5.3), and (5.4), the mean deviation about mean, and the mean deviation about median, of Adya distribution are obtained as

${\delta }_1\left(X\right)=\frac{2\left\{2{\theta }^3\mu +{\theta }^2({\mu }^2+\mu )+4\theta \mu +\left({\theta }^4+6\right)\right\}{e}^{-\theta \mu }}{\theta \left({\theta }^4+2{\theta }^2+2\right)}$ (5.5)

${\delta }_2\left(X\right)=\frac{2\left\{{\theta }^{5}M+{\theta }^4\left(2M^2+1\right)+{\theta }^3(M^3+4M)+{\theta }^2(3M^2+M)+6\theta M+6\right\}{e}^{-\theta M}}{\theta \left({\theta }^4+2{\theta }^2+2\right)}-\mu$ (5.6)

The Bonferroni⁸ and Lorenz curves are defined as

$B\left(p\right)=\frac{1}{p\mu }{\displaystyle \underset{0}{\overset{q}{\int }}xf\left(x\right)}dx=\frac{1}{p\mu }\left[{\displaystyle \underset{0}{\overset{\infty }{\int }}xf\left(x\right)dx-}{\displaystyle \underset{q}{\overset{\infty }{\int }}xf\left(x\right)}dx\right]=\frac{1}{p\mu }\left[\mu -{\displaystyle \underset{q}{\overset{\infty }{\int }}xf\left(x\right)}dx\right]$ (6.1)

 and $L\left(p\right)=\frac{1}{\mu }{\displaystyle \underset{0}{\overset{q}{\int }}xf\left(x\right)}dx=\frac{1}{\mu }\left[{\displaystyle \underset{0}{\overset{\infty }{\int }}xf\left(x\right)dx-}{\displaystyle \underset{q}{\overset{\infty }{\int }}xf\left(x\right)}dx\right]=\frac{1}{\mu }\left[\mu -{\displaystyle \underset{q}{\overset{\infty }{\int }}xf\left(x\right)}dx\right]$ (6.2)

 respectively or equivalently

$B\left(p\right)=\frac{1}{p\mu }{\displaystyle \underset{0}{\overset{p}{\int }}{F}^{-1}\left(x\right)}dx$ (6.3)

 and $L\left(p\right)=\frac{1}{\mu }{\displaystyle \underset{0}{\overset{p}{\int }}{F}^{-1}\left(x\right)}dx$ (6.4)

 respectively, where $\mu =E\left(X\right)$ and $q=F^{-1}\left(p\right)$ .

 The Bonferroni and Gini indices are thus defined as

$B=1-{\displaystyle \underset{0}{\overset{1}{\int }}B\left(p\right)}dp$ (6.5)

 and $G=1-2{\displaystyle \underset{0}{\overset{1}{\int }}L\left(p\right)}dp$ (6.6)

 respectively.

 Using pdf (1.2), we have

${\displaystyle \underset{q}{\overset{\infty }{\int }}xf\left(x\right)}dx=\frac{\left\{{\theta }^{5}q+{\theta }^4(2q^2+1)+{\theta }^3(q^3+4q)+{\theta }^2(3q^2+1)+6\theta q+6\right\}{e}^{-\theta q}}{\theta \left({\theta }^4+2{\theta }^2+2\right)}$ (6.7)

Now using equation (6.7) in (6.1) and (6.2), we have

$B\left(p\right)=\frac{1}{p}\left[1-\frac{\left\{{\theta }^{5}q+{\theta }^4(2q^2+1)+{\theta }^3(q^3+4q)+{\theta }^2(3q^2+4)+6\theta q+6\right\}{e}^{-\theta q}}{{\theta }^4+4{\theta }^2+6}\right]$ (6.8)

 and$L\left(p\right)=1-\frac{\left\{{\theta }^{5}q+{\theta }^4(2q^2+1)+{\theta }^3(q^3+4q)+{\theta }^2(3q^2+4)+6\theta q+6\right\}{e}^{-\theta q}}{{\theta }^4+4{\theta }^2+6}$ (6.9)

 Now using equations (6.8) and (6.9) in (6.5) and (6.6), the Bonferroni and Gini indices are obtained as

$B=1-\frac{\left\{{\theta }^{5}q+{\theta }^4(2q^2+1)+{\theta }^3(q^3+4q)+{\theta }^2(3q^2+4)+6\theta q+6\right\}{e}^{-\theta q}}{{\theta }^4+4{\theta }^2+6}$ (6.10)

$G=\frac{2\left\{{\theta }^{5}q+{\theta }^4(2q^2+1)+{\theta }^3(q^3+4q)+{\theta }^2(3q^2+4)+6\theta q+6\right\}{e}^{-\theta q}}{{\theta }^4+4{\theta }^2+6}-1$ (6.11)

Suppose $X$ and $Y$ be independent strength and stress random variables having Adya distribution with parameter ${\theta }_1$ and ${\theta }_2$ respectively. Then $R=P\left(Y<X\right)$ is known as stress-strength parameter and is a measure of the component reliability.

Thus, $R=P\left(Y<X\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}P\left(Y<X|X=x\right)}{f}_X\left(x\right)dx={\displaystyle \underset{0}{\overset{\infty }{\int }}f\left(x;{\theta }_1\right)}F\left(x;{\theta }_2\right)dx$ $=1-\frac{{\theta }_1{}^3\left[\begin{array}{l}24{\theta }_2{}^2+12{\theta }_2^{}\left({\theta }_2^2+{\theta }_1{\theta }_2+1\right)({\theta }_1+{\theta }_2)+2\left({\theta }_2^4+4{\theta }_1{\theta }_2^3+{\theta }_1^2{\theta }_2^2+2{\theta }_2^2+4{\theta }_1{\theta }_2+2\right){(}^{{\theta }_1}\\ +2{\theta }_1\left({\theta }_2{}^4+{\theta }_1{\theta }_2{}^3+2{\theta }_2+{\theta }_1{\theta }_2+2\right){\left({\theta }_1+{\theta }_2\right)}^3+{\theta }_1^2({\theta }_2^4+2{\theta }_2^2+2){\left({\theta }_1+{\theta }_2\right)}^4\end{array}\right]}{\left({\theta }_1{}^4+2{\theta }_1^2+2\right)\left({\theta }_2{}^4+2{\theta }_2^2+2\right){\left({\theta }_1+{\theta }_2\right)}^5}$ $=1-\frac{{\theta }_1{}^3\left[\begin{array}{l}24{\theta }_2{}^2+12{\theta }_2^{}\left({\theta }_2^2+{\theta }_1{\theta }_2+1\right)({\theta }_1+{\theta }_2)+2\left({\theta }_2^4+4{\theta }_1{\theta }_2^3+{\theta }_1^2{\theta }_2^2+2{\theta }_2^2+4{\theta }_1{\theta }_2+2\right){(}^{{\theta }_1}\\ +2{\theta }_1\left({\theta }_2{}^4+{\theta }_1{\theta }_2{}^3+2{\theta }_2+{\theta }_1{\theta }_2+2\right){\left({\theta }_1+{\theta }_2\right)}^3+{\theta }_1^2({\theta }_2^4+2{\theta }_2^2+2){\left({\theta }_1+{\theta }_2\right)}^4\end{array}\right]}{\left({\theta }_1{}^4+2{\theta }_1^2+2\right)\left({\theta }_2{}^4+2{\theta }_2^2+2\right){\left({\theta }_1+{\theta }_2\right)}^5}$

Since Adya distribution has one parameter, equating the population mean to the corresponding sample mean, the moment estimate $\tilde{\theta }$ of $\theta$ is the solution of the following fifth degree polynomial equation $\overline{x}{\theta }^5-{\theta }^4+2\overline{x}{\theta }^3-4{\theta }^2+2\theta \overline{x}-6=0$

, where $\overline{x}$ is the sample mean.

Estimation using maximum likelihood estimation

Taking $\left(x_1,x_2,x_3,\mathrm{...},x_n\right)$ a random sample from (1.2), the natural log likelihood function of Adya distribution is

$\ln L=n\ln \left(\frac{{\theta }^3}{{\theta }^4+2{\theta }^2+2}\right)+2{\displaystyle \sum _{i=1}^n\ln \left(\theta +x_i\right)}-n\theta \overline{x}$ .

This gives,$\frac{d\ln L}{d\theta }=\frac{3n}{\theta }-\frac{4n\theta \left({\theta }^2+1\right)}{{\theta }^4+2{\theta }^2+2}+2{\displaystyle \sum _{i=1}^n\frac{1}{\theta +x_i}}-n\overline{x}$ ,

The MLE $\tilde{\theta }$ of $\theta$ is the solution of $\frac{d\ln L}{d\theta }=0$ which is given by

$\frac{3n}{\theta }-\frac{4n\theta \left({\theta }^2+1\right)}{{\theta }^4+2{\theta }^2+2}+2{\displaystyle \sum _{i=1}^n\frac{1}{\theta +x_i}}-n\overline{x}=0$ .

This non-linear equation is not in compact form and its solution can be obtained analytically. We have to use non-linear optimization technique such as quasi-Newton algorithm available in R software to maximize the log-likelihood function.

A simulation study has been conducted to examine the performance of the maximum likelihood estimate (MLE) of the parameter of Adya distribution. Random number $n=20,40,60$ and 80 generated corresponding to the parameter $\theta =0.1,0.2,0.3,0.4$ and 0.5 using Acceptance- Rejection method. Its Bias and Mean Square Error have been calculated and presented in the table 3.

The data set considered for the goodness of fit of Adya distribution is the strength data of glass of the aircraft window reported by Fuller et al.⁹ and are given as

18.83, 20.80, 21.657, 23.03, 23.23, 24.05, 24.321, 25.50, 25.52, 25.80, 26.69, 26.77, 26.78, 27.05, 27.67, 29.90, 31.11, 33.20, 33.73, 33.76, 33.89, 34.76, 35.75, 35.91, 36.98, 37.08, 37.09, 39.58, 44.045, 45.29, 45.381        

The goodness of fit of the distributions are based on the values of $-2\ln L$ , AIC (Akaike Information Criterion) and K-S (Kolmogorov-Smirnov) statistic. AIC and K-S are computed using,$AIC=-2\ln L+2k$ ,$K\text{-}S=\underset{x}{\text{Sup}}\left|F_n\left(x\right)-F_0\left(x\right)\right|$ where $k$ = the number of parameters, $n$ = the sample size and $F_n\left(x\right)$ is the empirical distribution function. The distribution having lower $-2\ln L$ , AIC , and K-S are said to be best distribution. The MLE $\left(\widehat{\theta }\right)$ and standard error, S.E$\left(\widehat{\theta }\right)$ of$\theta$ ,$-2\ln L$ , AIC, K-S and p-value of the fitted distributions are presented in the table 4.

Clearly Adya distribution gives better fit than Shanker, Aradhana, Sujatha, Devya, Lindley and exponential distributions.

Adya distribution, a one parameter lifetime distribution, for modeling lifetime data has been presented and studied. The statistical properties including coefficient of variation, skewness, kurtosis, index of dispersion, hazard rate function, mean residual life function, stochastic ordering, mean deviations, Bonferroni and Lorenz curves and stress-strength reliability have been discussed. Over-dispersed, equi-dispersed, and under-dispersed of Adya distribution are presented. Method of moment and method of maximum likelihood are explained for estimating parameter. The asymptotic property of the ML estimate of the parameter has been discussed with simulation study. Finally, the goodness of fit test has been presented with a real lifetime data.

NOTE: The paper is named Adya distribution in the name of my loving niece Adya Vedanshi, the daughter of my younger brother Dr. Ravi Shanker.

None.

All authors declare that there is no conflict of interest.

1. Lindley DV. Fiducial distributions and Bayes’ theorem, Journal of the Royal         Statistical Society, Series B. 1958;20:102‒107.
2. Shanker R, Hagos F, and Sujatha S. On modeling of lifetimes data using and lindley distributions, Biometrics & Biostatistics International Journal. 2015;2(5):1‒9.
3. Shanker R. Shanker distribution and its Applications, International Journal of       Statistics and Applications. 2015;5(6):338‒348.
4. Shanker R. Aradhana distribution and its Applications, International Journal of Statistics and Applications. 2016;6(1):23–34.
5. Shanker R. Sujatha distribution and its Applications, Statistics in Transition-          new series. 2016;17(3):391‒410.
6. Shanker R. Devya distribution and its Applications, International Journal of          Statistics and Applications. 2016;6(4):189–202.
7. Shaked M, Shanthikumar JG. Stochastic orders and their applications, Academic Press, New York; 1994.
8. Bonferroni CE. On a sum and difference of two quasi lindley distributions: Theory and applications. Elementi di Statistca generale, Seeber, Firenze. 1930;9(1):12–23.
9. Fuller EJ, Frieman S, Quinn J, et al. Fracture mechanics approach to the design of glass aircraft windows: A case study, SPIE Proc. 1994;2286:419‒430.