A simulation study on ishita distribution

doi:10.15406/bbij.2017.06.00173

eISSN: 2378-315X

Biometrics & Biostatistics International Journal

Research Article Volume 6 Issue 4

A simulation study on ishita distribution

Kamlesh Kumar Shukla, Rama Shanker

Verify Captcha

Regret for the inconvenience: we are taking measures to prevent fraudulent form submissions by extractors and page crawlers. Please type the correct Captcha word to see email ID.

Department of Statistics, Eritrea Institute of Technology, Eritrea

Correspondence: Rama Shanker, Department of Statistics, Eritrea Institute of Technology, Asmara, Eritrea

Received: October 06, 2017 | Published: October 23, 2017

Citation: Shukla KK, Shanker R. A simulation study on ishita distribution. Biom Biostat Int J. 2017;6(4):381-386. DOI: 10.15406/bbij.2017.06.00173

Download PDF

Abstract

In this paper, a simulation study on Ishita distribution proposed by Shanker and Shukla¹ has been carried out and presented. Average bias, mean square error and confidence interval of the parameter have been given for simulated data. Profile of likelihood estimator for the parameter has been illustrated graphically along with goodness of fit on real life time data. the goodness of fit has been established with an example from engineering and the fit has been compared with other one parameter lifetime distributions.

Introducton

A Simulation study is a computer programming which represent the real world based model. The accuracy of the simulation depends on the precision of the model. For example, suppose that the probability of head in a tossing a coin is unknown. The experiment of tossing a coin be perfomed $n$ times repetitively to approximate the probability of head. That is

P(H)= Number of times head observed/ Number of times the experiment performed.

There are many situations where it is not possible to determine the probabilities by executing experiments a large number of times. Now a day using high level programming language R such problems are solved by generating random numbers to deal with problem.

It is crucial to generate random number for mathematical model especially probabilistic model. To use simulation, it is necessary to generate the sample random events that make up the model with the help of a computer to reproduce the process through which chance is generated in the actual situation. Thus, a problem that involves many interrelationships among random variables can evaluate as a function of given parameters.

During a short span of time a number of lifetime distributions have been introduced in statistical literature. The important one parameter classical lifetime distributions which are popular in statistics are exponential distribution and Lindley distribution introduced by Lindley.² Ghitany et al.³ have detailed discussion about various properties of Lindley distribution along with the estimation of parameter and application. Shanker et al.⁴ have done extensive study on comparative study on modeling of lifetime data from biomedical science and engineering using exponential and Lindley distributions and concluded that there are several lifetime data where these classical distributions are not suitable due to their theoretical nature or application point of view. In search for new lifetime distributions which gives better fit than both exponential and Lindley distributions, Shanker^5-7 has introduced four one parameter lifetime distributions namely, Shanker, Akash, Aradhana and Sujatha and showed that these lifetime distributions gives better fit than both exponential and Lindley distributions., In fact, it has been established by Shanker^5-7 that these distributions have advantage over each other. The probability density function (pdf) and the cumulative distribution function (cdf) of exponential, Lindley, Shanker, Akash, Aradhana and Sujatha distributions are presented in table 1.

Distributions	Probability density function(cdf)	Cumulative distribution function (cdf)
Ishita	$f (x) = \frac{θ^{3}}{θ^{3} + 2} (θ + x^{2}) e^{- θ x}$	$F (x) = 1 - [1 + \frac{θ x (θ x + 2)}{θ^{3} + 2}] e^{- θ x}$
Sujatha	$f (x) = \frac{θ^{3}}{θ^{2} + θ + 2} (1 + x + x^{2}) e^{- θ x}$	$F (x) = 1 - [1 + \frac{θ x (θ x + θ + 2)}{θ^{2} + θ + 2}] e^{- θ x}$
Aradhana	$f (x) = \frac{θ^{3}}{θ^{2} + 2 θ + 2} {(1 + x)}^{2} e^{- θ x}$	$F (x) = 1 - [1 + \frac{θ x (θ x + 2 θ + 2)}{θ^{2} + 2 θ + 2}] e^{- θ x}$
Akash	$f (x) = \frac{θ^{3}}{θ^{2} + 2} (1 + x^{2}) e^{- θ x}$	$F (x) = 1 - [1 + \frac{θ x (θ x + 2)}{θ^{2} + 2}] e^{- θ x}$
Shanker	$f (x) = \frac{θ^{2}}{θ^{2} + 1} (θ + x) e^{- θ x}$	$F (x) = 1 - [1 + \frac{θ x}{θ^{2} + 1}] e^{- θ x}$
Lindley	$f (x) = \frac{θ^{2}}{θ + 1} (1 + x) e^{- θ x}$	$F (x) = 1 - [1 + \frac{θ x}{θ + 1}] e^{- θ x}$
Exponential	$f (x) = θ e^{- θ x}$	$F (x) = 1 - e^{- θ x}$

Table 1 pdf and cdf of exponential, Lindley, Shanker, Akash, Aradhana, Sujatha and Ishita distributions ( $x > 0, θ > 0$ )

Recently, Shanker and Shukla¹ have proposed a new lifetime distribution named Ishita distribution for modeling lifetime distribution and showed that it gives better fit than exponential, Lindley, Shanker, Akash, Aradhana and Sujatha distributions. Detailed study about various mathematical and Statistical properties, estimation of parameter and applications of Ishita distribution are available in Shanker and Shukla.¹

It seems that Ishita distribution has not been fully studied by Shanker and Shukla.¹ In this paper firstly some graphs of pdf and cdf of Ishita distribution has been drawn for varying values of parameters to know its nature. Its coefficients of variation, skewness, kurtosis and index of dispersion have been studied graphically. A simulation study has been conducted and its average bias, mean square error and confidence interval have been presented for simulated data. Profile of the likelihood estimator for parameter along with its goodness of fit has been illustrated graphically. Finally an example has been discussed for testing goodness of fit of Ishita distribution along with other one parameter lifetime distributions.

Descriptive properties of ishita distribution

The graphs of pdf and cdf of Ishita distribution are shown in figure 1 and 2. From the graphs of pdf it is obvious that Ishita distribution is monotonically decreasing. As the value of parameter $θ$ increases, the graphs start upward but for increasing values of $x$ it start decreasing at faster rate. Similarly the graphs of cdf shows that for increasing values of the parameter $θ$ , it becomes concave downward.

The coefficient of variation (C.V.), coefficient of skewness $(\sqrt{β_{1}})$ , coefficient of kurtosis $(β_{2})$ and index of dispersion $(γ)$ of Ishita distribution obtained by Shanker and Shukla¹ are given by

$C . V . = \frac{(θ^{6} + 16 θ^{3} + 12) {}^{1 / 2}}{θ^{3} + 6}$

$\sqrt{β_{1}} = \frac{2 (θ^{9} + 30 θ^{6} + 36 θ^{3} + 24)}{{(θ^{6} + 16 θ^{3} + 12)}^{3 / 2}}$

$β_{2} = \frac{3 (θ^{12} + 128 θ^{9} + 408 θ^{6} + 576 θ^{3} + 240)}{{(θ^{6} + 16 θ^{3} + 12)}^{2}}$

$γ = \frac{θ^{6} + 16 θ^{3} + 12}{θ (θ^{3} + 2) (θ^{3} + 6)}$

Figure 1 Graph of pdf of the Ishita distribution for different values of the parameter $θ$ .

Figure 2 Graphs cdf of Ishita distribution for different values of the parameter $θ$ .

Graphs of coefficient of variation, coefficient of skewness, coefficient of kurtosis and the index of dispersion of Ishita distribution are shown in figure 3. From the graphs it is obvious that coefficient of variation, coefficient of skewness and coefficient of kurtosis are initially increasing for increasing values of parameter $θ$ but later on start decreasing slowly for increasing values of parameter $θ$ . The graph of index of dispersion is decreasing for increasing values of parameter $θ$ .

Figure 3a Graphs of Coefficient of Variation, coefficient of Skewness, coefficient of Kurtosis and Index of dispersion of Ishita distribution for varying values of parameter $θ$ .

Figure 3b Estimated mean squared error of the MLEs for different values of $θ$ and $n$ .

The plots between simulated and estimated values of parameter $θ$ are shown in figure 4.

A simulation study

In this section, we seek to evaluate the numerous properties of the proposed technique by performing a simulation study. This process consists in generating N=10,000 pseudo-random samples of sizes 20, 40, 60, 80, 100 from Ishita distribution. Acceptance and rejection method has been used for the simulation of data. Average bias and mean square error of the MLEs of the parameter $θ$ are estimated using the following formulae

$A v e r a g e B i a s = \frac{1}{N} \sum_{j = 1}^{N} ({\overset{⌢}{θ}}_{j} - θ), M S E (θ) = \frac{1}{N} {\sum_{j = 1}^{N} ({\overset{⌢}{θ}}_{j} - θ)}^{2}$

The following algorithm can be used to generate random sample from Ishita distribution. The process to generate a random sample consists of running the algorithm as often as necessary, say $n$ times.

Algorithm

Rejection method: To simulate from the density $f_{X}$ , it is assumed that we have envelope density h from which it can simulate, and that we have some $k < \infty$ such that $s u p_{x} \frac{f_{X} (x)}{h (x)} \leq k$

Simulate X from h.

Generate $Y ~ U (0, k h (X)$ , where $k = \frac{θ^{3}}{θ^{3} + 2}$
If $Y < f_{x} (X)$ then return X, otherwise go back to step 1.

The average bias (mean square error) of simulated estimate of parameter $θ$ is presented in table 2.

$n$	Parameter $θ$
$n$	0.5	1	2	3
20	0.12529(0.1252)	0.04534 (0.04113)	-0.03517 (0.0247)	-0.0987(0.19485)
40	0.054755(0.11992)	0.01868 (0.01396)	-0.02022 (0.0163)	-0.0515(0.10648)
60	0.038151(0.08732)	0.013337(0.01067)	-0.0129 (0.00999)	-0.0339(0.069003)
80	0.028079(0.06307	0.00975 (0.00761)	-0.0098(0.00773)	-0.0255(0.05236)
100	0.021859(0.047783)	0.00748(0.00560)	-0.0080(0.00653)	-0.0206(0.04268)

Table 2 Average bias (mean square error) of the simulated estimates of parameter $θ$

Values of the estimate of parameter, standard error, -2logL, AIC and Confidence Interval (C.I) for simulated data on N=10,000 for different values of parameter are presented in table 3.

$θ$	Estimates of $\hat{θ}$	S.E.	-2logL	AIC	C. I.
$θ$	Estimates of $\hat{θ}$	S.E.	-2logL	AIC	Lower	Upper
0.4	2.907545	0.0221610	1502.83	1504.83	2.86446	2.95133
0.5	2.486496	0.01728233	5975.21	5977.217	2.45288	2.52063
0.8	1.860619	0.010777	15372.96	15374.96	1.83963	1.88188
0.9	1.740233	0.0097021	17728.03	17730.03	1.721330	1.759362
1	1.641053	0.0088720	19840.31	19842.31	1.623761	1.65854
1.2	1.484858	0.00767496	23521.97	23523.97	1.469890	1.499976
1.5	1.314178	0.00652887	28113.48	28115.48	1.301434	1.327027
2.0	1.117259	0.00541481	34273.16	342735.16	1.106683	1.127909
2.5	0.9766439	0.00473939	39311.69	39313.69	0.9673826	0.9859608
3	0.8674364	0.004265468	43620.11	43622.11	0.8590990	0.8758194

Table 3 Values of estimate of parameter, standard error, -2logL, AIC and Confidence Interval for simulated data at N=10,000 on different values of $θ$

The graphs of estimated mean square error of the maximum likelihood estimate (MLE) for different values of parameter $θ$ and $n$ have been shown in figure 3.

Data analysis

In this section Ishtita distribution has been used to model for data which is due to Birnbaum and Saunders⁸ on the fatique life of 6061-T6 aluminum coupons cut parallel to direction of rolling and oscillated at 18 cycles per second. The goodness of fit of the Ishita distribution has been compared with one parameter Akash, Sujatha, Shanker, Aradhana, Lindley and Exponential distributions.

Data Set: The data is given by Birnbaum and Saunders⁸ on the fatigue life of 6061 – T6 aluminum coupons cut parallel to the direction of rolling and oscillated at 18 cycles per second. The data set consists of 101 observations with maximum stress per cycle 31,000 psi. The data are presented below (after subtracting 65).

5	25	31	32	34	35	38	39	39	40	42 43	43	43	44
	44	47	47	48	49	49	49 51	54	55	55 55 56		56
	56	58	59	59 59	59	59	63	63	64 64	65	65	65
	66 66	66	66	66	67	67	67	68 69	69	69 69	71	71
	72	73	73	73	74	74	76 76 77		77	77	77	77
	77	79	79	80	81	83 83 84		86	86	87	90	91
	92	92	92	92 93	94	97 98	98	99	101	103	105	109
	136 147

In order to compare the goodness of fit of Ishita with Akash, Shanker Sujatha, Aradhana, Lindley and exponential distributions, $- 2 \ln L$ , AIC (Akaike Information Criterion),) of distributions for real lifetime data set have been computed and presented in table 4. The formulae for computing AIC and K-S statistic as follows:

$A I C = - 2 \ln L + 2 k$ , $B I C = - 2 \ln L + k \ln n$ , where $k$ the number of parameters, $n$ = the sample size $D = \sup_{x} | F_{n} (x) - F_{0} (x) |$ , where $k$ = the number of parameters, $n$ = the sample size and $F_{n} (x)$ is the empirical distribution function. The best distribution is the distribution which corresponds to lower values of $- 2 \ln L$ , AIC and K-S statistics.

The fitted plot of one parameter lifetime distributions and profile of likelihood estimate of parameter plot for data set has been presented in figure 5.

Distributions	Parameters estimates( $\hat{θ}$ )	S.E( $\hat{θ}$ )	-2logL	AIC	K-S
Ishita	0.04390977	0.002533	950.91	952.91	0.193
Akash	0.0438789	0.002531	950.97	952.97	0.194
Sujatha	0.0435654	0.002513	951.78	953.78	0.195
Aradhana	0.0432677	0.002496	952.58	954.58	0.196
Shanker	0.029263	0.002065	980.97	982.97	0.248
Lindley	0.0288712	0.002039	983.10	985.10	0.252
Exponential	0.014634	0.001456	1044.87	1046.87	0.367

Table 4 MLEs $\hat{θ}$ ,SE( $\hat{θ}$ ,-2logL,AIC and K-S statistic for one parameter lifetime distributions

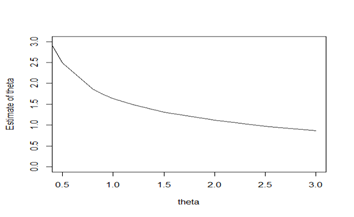
Figure 4 Plot between simulated values of theta and estimated values of theta.

Figure 5 Fitted plot of distributions and profile of likelihood estimate of parameter plot for data set.

Conclusions

A simulation study on Ishita distribution proposed by Shanker and Shukla¹ has been discussed and presented. Average bias, mean square error and confidence interval of the parameter have been studied for simulated data from Ishita distribution. Profile of likelihood estimator for the parameter has been illustrated graphically. The goodness of fit for Ishita distribution has been discussed with an example from engineering and the fit has been compared with some one parameter lifetime distributions. The goodness of fit of Ishita distribution shows that it can be considered an important lifetime distribution for modeling lifetime data from engineering.