In this paper, a quasi exponential distribution has been proposed and studied. Its statistical properties including moments, survival function, hazard rate function, mean residual life function and stochastic ordering have been discussed. Maximum likelihood estimation has been discussed for estimating the parameter of the distribution. Application of the distribution has been explained with a real lifetime data from biomedical science and its goodness of fit shows quite satisfactory over exponential distribution.

Keywords: exponential distribution, moments, hazard rate function, mean residual life function, stochastic ordering, parameter estimation, application.

The exponential distribution having scale parameter  (also known as rate parameter for failure, death, arrival etc) is defined by its probability density function (pdf) and cumulative distribution function (cdf)

$f_1\left(x;\theta \right)=\theta e^{-\theta x};x>0,\theta >0$           (1.1)

$F_1\left(x;\theta \right)=1-e^{-\theta x};x>0,\theta >0$           (1.2)

The exponential distribution provides a simple, elegant and closed form solution to many problems in lifetime testing and reliability studies. One reason for the wide popularity of the exponential distribution in reliability is that it is the limiting lifetime distribution of a series system of substantially similar components. Also the exponential distribution is important due to its memory loss property. However, the exponential distribution does not provide a significant fit for some real lifetime applications, where the failure rates are not constant. Epstein¹ has detailed study on exponential distribution and its role in life testing. Sato et al.² obtained a discrete exponential distribution and discussed its properties and applied the distribution to model defect count distribution in semi-conductor deposition equipment and defect count distribution per chips. Gupta & Kundu³ have introduced generalized exponential distribution and discussed its properties and applications. Most of the works done on exponential distribution, its extension, mixture and applications in different fields of knowledge are available in Ahsanullah &Hamedani.⁴ Although exponential distribution was the first one parameter lifetime distribution for modeling lifetime data from engineering and biomedical sciences, but due to one parameter it is not always a suitable lifetime distribution. Also the hazard rate function and the mean residual life function of exponential distribution are always constant.

The statistical modeling and analysis of lifetime data are crucial in almost all branches of knowledge especially engineering and biomedical sciences. The one parameter exponential distribution is popular in statistics literature for modeling lifetime data. It has been observed that exponential distribution is not always a suitable model either due to theoretical or applied point of view. An attempt has been made to find a one parameter lifetime distribution which competes well with exponential distribution.

In this paper a quasi exponential distribution has been proposed. Its statistical properties including shapes of pdf for varying values of parameter, moments, hazard rate function, mean residual life function, stochastic ordering have been discussed. Estimation of parameter has been discussed using maximum likelihood estimation. Finally, application to a real lifetime data from biomedical science has been presented to test its goodness of fit over exponential distribution.

A quasi exponential distribution (QED) having scale parameter $\theta$ is defined by its pdf

&$f_2\left(x;\theta \right)=\frac{2{\theta }^{1/2}}{\Gamma \left(\frac{1}{2}\right)}{e}^{-\theta x^2};x>0,\theta >0$           (2.1)

The survival (reliability) function of QED (2.1) can be obtained as

$S\left(x;\theta \right)=P\left(X>x\right)=\frac{2{\theta }^{1/2}}{\Gamma \left(\frac{1}{2}\right)}{\displaystyle \underset{x}{\overset{\infty }{\int }}{e}^{-\theta t^2}}dt=\frac{\Gamma \left(\frac{1}{2},\theta x^2\right)}{\Gamma \left(\frac{1}{2}\right)};x>0,\theta >0$         (2.2)

Where the function  is the upper incomplete gamma function defined as

$\Gamma \left(\alpha ,z\right)={\displaystyle \underset{z}{\overset{\infty }{\int }}{e}^{-y}{y}^{\alpha -1}dy;\alpha >0,z\ge 0}$,          (2.3)

Thus the cdf of QED (2.1) can be defined as

$F_2\left(x;\theta \right)=1-S\left(x;\theta \right)=1-\frac{\Gamma \left(\frac{1}{2},\theta x^2\right)}{\Gamma \left(\frac{1}{2}\right)};x>0,\theta >0$     (2.4)

The behavior of the pdf and cdf of QED and exponential distribution (ED) for varying values of parameter have been shown in figures 1 and 2 respectively.

The r^th moment about origin of QED can be obtained as

${\mu }_r^{\prime }=E\left(X^r\right)=\frac{2{\theta }^{1/2}}{\Gamma \left(\frac{1}{2}\right)}{\displaystyle \underset{0}{\overset{\propto }{\int }}{e}^{-\theta x^2}}{x}^{r}dx=\frac{\Gamma \left(\frac{r+1}{2}\right)}{{\theta }^{r/2}\Gamma \left(\frac{1}{2}\right)};r=1,2,3,\mathrm{....}$      (3.1)

&${\mu }_r^{\prime }=E\left(X^r\right)=\frac{2{\theta }^{1/2}}{\Gamma \left(\frac{1}{2}\right)}{\displaystyle \underset{0}{\overset{\propto }{\int }}{e}^{-\theta x^2}}{x}^{r}dx=\frac{\Gamma \left(\frac{r+1}{2}\right)}{{\theta }^{r/2}\Gamma \left(\frac{1}{2}\right)};r=1,2,3,\mathrm{....}$

Taking $r=1,2,3,and4$;in (3.1), the first four moments about origin of QED are obtained as

${\mu }_1^{\prime }=\frac{1}{{\theta }^{1/2}\Gamma \left(\frac{1}{2}\right)}$, ${\mu }_2^{\prime }=\frac{1}{2\theta }$, ${\mu }_3^{\prime }=\frac{1}{{\theta }^{3/2}\Gamma \left(\frac{1}{2}\right)}$;and ${\mu }_4^{\prime }=\frac{3}{4{\theta }^2}$

The variance of QED can be obtained as

${\mu }_2=\frac{{\left(\Gamma \left(\frac{1}{2}\right)\right)}^2-2}{2\theta {\left(\Gamma \left(\frac{1}{2}\right)\right)}^2}$.

The third and fourth central moments are not being given here because their expressions are lengthy. However, they can be calculated using relationship${\mu }_r=E{\left(Y-{\mu }_1^{\prime }\right)}^r={\displaystyle \sum _{k=0}^r\left(\begin{array}{c}r\\ k\end{array}\right)}{\mu }_k^{\prime }{\left(-{\mu }_1^{\prime }\right)}^{r-k}$ ;between central moments and moments about mean.

Let $X$ be a continuous random variable with pdf $f\left(x\right)$ and cdf $F\left(x\right)$ . The hazard rate     function (also known as the failure rate function) and the mean residual life                 function of are respectively defined as

$h\left(x\right)=\underset{\Delta x\to 0}{lim}\frac{P\left(X<x+\Delta x|X>x\right)}{\Delta x}=\frac{f\left(x\right)}{1-F\left(x\right)}$          (4.1)

and $m\left(x\right)=E\left[X-x|X>x\right]=\frac{1}{1-F\left(x\right)}{\displaystyle {\int }_x^{\infty }\left[1-F\left(t\right)\right]}dt$ $=\frac{1}{S\left(x\right)}{\displaystyle \underset{x}{\overset{\infty }{\int }}tf\left(t\right)dt-x}$        (4.2)

The corresponding hazard rate function,$h\left(x\right)$ and the mean residual life function,$m\left(x\right)$ of QED (2.1) are obtained as

$h\left(x\right)=\frac{2{\theta }^{1/2}{e}^{-\theta x^2}}{\Gamma \left(\frac{1}{2},\theta x^2\right)}$        (4.3)

and

$m\left(x\right)=\frac{1}{S\left(x;\theta \right)}{\displaystyle \underset{x}{\overset{\infty }{\int }}t{f}_2\left(t;\theta \right)dt-x}=\frac{\Gamma \left(1,\theta x^2\right)}{{\theta }^{1/2}\Gamma \left(\frac{1}{2},\theta x^2\right)}-x$ $=\frac{e^{-\theta x^2}}{{\theta }^{1/2}\Gamma \left(\frac{1}{2},\theta x^2\right)}-x$       (4.4)

The hazard rate function and the mean residual life function of the QED show flexibility over exponential distribution because in case of exponential distribution these measures are always constant. The behavior of  and  of QED for varying values of parameter are shown in Figure 3 &Figure 4.

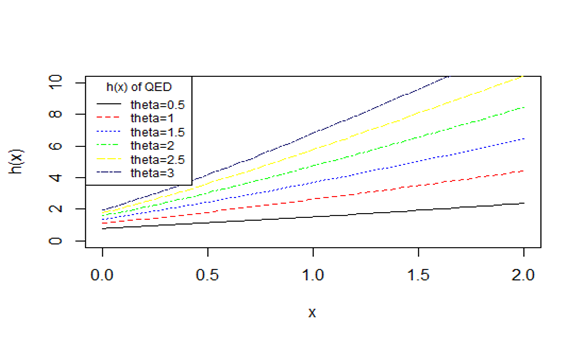
Figure 3 Behavior of the hazard rate function of QED for varying values of parameter $\theta$ .

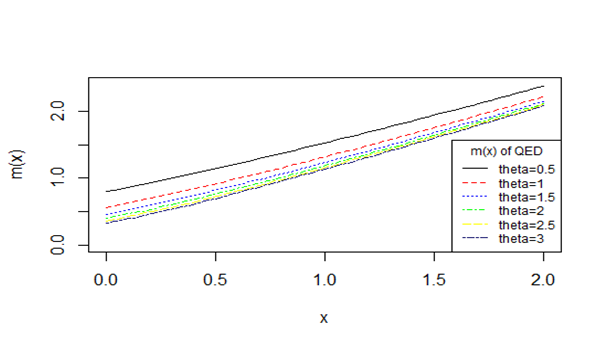
Figure 4Behavior of the mean residual life function of QED for varying values of parameter $\theta$ .

Stochastic ordering of positive continuous random variables is an important tool for judging their comparative behavior.⁶ A random variable $X$ is said to be smaller than a random variable $Y$ in the

1. stochastic order $\left(X{\le }_{st}Y\right)$ if $F_X\left(x\right)\ge F_Y\left(x\right)$ for all $x$
2. hazard rate order $\left(X{\le }_{hr}Y\right)$ if $h_X\left(x\right)\ge h_Y\left(x\right)$ for all $x$
3. mean residual life order $\left(X{\le }_{mrl}Y\right)$ if$m_X\left(x\right)\le m_Y\left(x\right)$ for all $x$
4. likelihood ratio$\left(X{\le }_{lr}Y\right)$ order if $\frac{f_X\left(x\right)}{f_Y\left(x\right)}$ decreases in$x$ .

The following results due to Shaked & Shanthikumar⁵ are well known for establishing stochastic ordering of distributions

$\begin{array}{l}X{\le }_{lr}Y\Rightarrow X{\le }_{hr}Y\Rightarrow X{\le }_{mrl}Y\\ \underset{X{\le }_{st}Y}{\Downarrow }\end{array}$

The QED is ordered with respect to the strongest ‘likelihood ratio ordering’ as established in the following theorem

Theorem: Let $X\to QED\left({\theta }_1,{\alpha }_1\right)$ and $Y\to QED\left({\theta }_2,{\alpha }_2\right)$ If ${\theta }_1>{\theta }_2$ , then $X{\le }_{lr}Y$ and hence$X{\le }_{hr}Y$ $X{\le }_{mrl}Y$ , and$X{\le }_{ST}Y$ .

Proof: We have

$\frac{f_X\left(x;{\theta }_1,{\alpha }_1\right)}{f_Y\left(x;{\theta }_2,{\alpha }_2\right)}={\left(\frac{{\theta }_1}{{\theta }_2}\right)}^{1/2}{e}^{-\left({\theta }_1-{\theta }_2\right)x^2};x>0$

Now, $ln\frac{f_X\left(x;{\theta }_1,{\alpha }_1\right)}{f_Y\left(x;{\theta }_2,{\alpha }_2\right)}=\frac{1}{2}ln\left(\frac{{\theta }_1}{{\theta }_2}\right)-\left({\theta }_1-{\theta }_2\right)x^2$

This gives

$\frac{d}{dx}\left\{ln\frac{f_X\left(x;{\theta }_1,{\alpha }_1\right)}{f_Y\left(x;{\theta }_2,{\alpha }_2\right)}\right\}=-2\left({\theta }_1-{\theta }_2\right)x$

Thus if${\theta }_1>{\theta }_2$ ,$\frac{d}{dx}\left\{ln\frac{f_X\left(x;{\theta }_1,{\alpha }_1\right)}{f_Y\left(x;{\theta }_2,{\alpha }_2\right)}\right\}<0$ . This means that $X{\le }_{lr}Y$ and hence $X{\le }_{hr}Y$ , $X{\le }_{mrl}Y$ and $X{\le }_{st}Y$ . This shows flexibility of QED over exponential distribution.

In this section, the estimation of parameters of QED has been discussed using method of maximum likelihood. Let $\left(x_1,x_2,\mathrm{...},x_n\right)$ be a random sample of size from the QED (2.1). The natural log likelihood function of QED (2.1) can be given by

$lnL=n\left[ln2+\frac{1}{2}ln\theta -ln\Gamma \left(\frac{1}{2}\right)\right]-\theta {\displaystyle \sum _{i=1}^n{x}_i{}^2}$

The maximum likelihood estimate (MLE) of the parameter  of QED (2.1) is the solutions of log likelihood equation

$\frac{dlnL}{d\theta }=\frac{n}{2\theta }-{\displaystyle \sum _{i=1}^n{x}_i{}^2}=0$

which gives

$\stackrel{\wedge }{\theta }=\frac{n}{2{\displaystyle \sum _{i=1}^n{x}_i{}^2}}=\frac{1}{\frac{2}{n}{\displaystyle \sum _{i=1}^n{x}_i{}^2}}$

Note that the method of moment estimate $\stackrel{\sim }{\theta }$ of the parameter $\theta$ is also the same as the MLE of the parameter.

The goodness of fit of the QGD has been explained with a real dataset from medical science. The following data represents the lifetime’s data relating to relief times (in minutes) of 20 patients receiving an analgesic and reported by Gross & Clark.⁶

1.1          1.4          1.3          1.7          1.9          1.8          1.6          2.2          1.7          2.7          4.1          1.8

1.5          1.2          1.4          3.0          1.7          2.3          1.6          2.0

For this data set, QED has been fitted along with one parameter exponential distribution.

The ML estimates,$-2lnL$ values of , Akaike Information criteria (AIC), and K-S statistics of the fitted distributions are presented in Table 1. The AIC and K-S Statistics are computed using the following formulae:

$AIC=-2lnL+2k$ ;and $K-S=\underset{x}{Sup}\left|F_n\left(x\right)-F_0\left(x\right)\right|$ ,

Where k= the number of parameters, n= the sample size,$F_n\left(x\right)$ is the empirical (sample) cumulative distribution function, and $F_0\left(x\right)$ is the theoretical cumulative distribution function. The best distribution is the distribution corresponding to lower values of , AIC, and K-S statistics. It is clear from the goodness of fit in Table 1 that QED gives better fit than exponential distribution and hence it can be considered an important lifetime distribution to model lifetime data from medical science.

The profiles of the likelihood estimate $\stackrel{\wedge }{\theta }$ of QED for the given dataset is presented in Figure 5. The fitted plots of the considered distributions for the given dataset are presented in Figure 6.

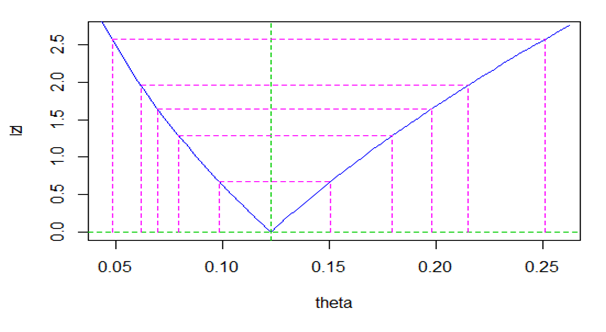
Figure 5 Profiles of the likelihood estimates of of QED for the considered dataset.

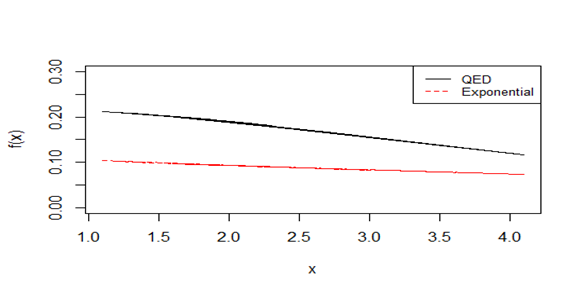
Figure 6 Fitted plots of the quasi exponential and exponential distributions for the given dataset.

This paper proposes a quasi exponential distribution for modeling real lifetime data from medical science. Its statistical properties including moments, survival function, hazard rate function, mean residual life function and stochastic ordering have been studied. The estimation of parameter has been discussed using maximum likelihood. Profile of the likelihood estimate of the parameter for QED has been shown graphically. Application of the distribution has been explained with a real lifetime data from biomedical science and its goodness of fit shows quite satisfactory over exponential distribution.

None.

Authors declares there is no conflict of interest.

1. Epstein B. The exponential distribution and its role in life testing. Industrial Quality control. 1958;15:2–7.
2. Sato H, Ikota M, Aritoshi S, et al. A new defect distribution in meteorology with consistent discrete exponential formula and its applications. IEEE Trans Semicond Manufactur. 1999;12(4):409–418.
3. Gupta RD, Kundu D. Generalized Exponential Distribution, Austalian & New Zealand Journal of Statistics. 1999;41(2):173–188.
4. Ahsanullah M, Hamedani GG. Exponential Distribution-Theory and Methods. New York: Nova Science Publishers, Inc.; 2010. p. 1–11.
5. Shaked M, Shanthikumar JG. Stochastic Orders and Their Applications. New York: Academic Press; 1994.
   
6. Gross AJ, Clark VA. Survival Distributions: Reliability Applications in the Biometrical Sciences. New York: John Wiley; 1975.