The von Mises distribution plays a pivotal role in circular data analysis. This paper addresses the question as to how much better one can do in estimating its concentration parameter if partial information is available on the mean direction, either (i) through a prior or (ii) through a “pre-test”. These two alternate scenarios and the resulting estimators are compared with the standard maximum likelihood estimator, and we explore when one estimator is superior to the other.

Keywords: preliminary test estimator, circular statistics, circular normal distribution, concentration parameter, maximum likelihood estimates, bayesian, mean square error, nuisance parameters

Saleh AME,¹ provides an introduction and thorough review on PTEs and Stein-type estimators for various linear models. In statistical inference, the use of prior information on other parameters in a statistical model, usually leads to improved inference on the parameter of interest. Prior information may he (i) known and deterministic which is then incorporated into the model in the form of constraints on the parameter space, leading to a restricted model, or (ii) uncertain and specified in the form of a prior distribution or a verified null hypothesis. In (ii), choosing certain restricted estimators may be justified when the prior information can be quantified i.e. comes with known confidence levels.

In some statistical models, certain parameters are of primary interest while other parameters may be considered as nuisance parameters. One procedure to mitigate the presence of nuisance parameters is to assess what value(s) such nuisance parameter(s) take, by a preliminary test with a null hypothesis restricting the nuisance parameter values. The null hypothesized value(s) of the nuisance parameter are either used or not, depending on whether the observed preliminary test statistic falls in the acceptance orrejection region of the hypothesis. That is, our final estimator for the parameter of interest is thus a linear combination, conditional on whether the preliminary test statistic is in the acceptance or rejection region of the test, and is called a Preliminary Test Estimator (PTE).^2,3 and⁴ were among the first to implement the idea of preliminary test estimation (PTE) in an analysis of variance (ANOVA) framework to analyze the effect of the preliminary test on the estimation of variance. The idea goes back to a suggestion in,⁵ which considers testing differences between two means after testing for the equality of variances; then using the usual t-test with the pooled estimate for variance, if the variance test shows equality; otherwise, it falls into the category of Behrens-Fisher problem. In these problems it became clear that the performance of the PTE depended heavily on the significance level of the preliminary test. Han c⁶ were the first to attempt to find an optimum size of significance level for the preliminary test for this two-sample problem.

All Stein-type estimators^7,8 involve appropriate test statistics for testing the adequacy of uncertain prior information on the parameter space, which is incorporated into the actual formulation of the estimator. Stein-type estimators adjust the unrestricted estimator by an amount of the difference between unrestricted and restricted estimators scaled by the adjusted test statistics for the uncertain prior information. Usually, the test statistics are the normalized distance between the unrestricted and restricted estimators and follow a noncentral chi-square or an F-distribution. The risk or the MSE of Stein-type estimators depends on the non-centrality parameter, which represents the distance between the full model and restricted model. The PTE may be considered a precursor of the Stein-type estimator. A simple replacement of the indicator function that we will see in the PTE with a multiple of the test statistic, leads to a Stein-type estimator.

The CND is the most widely used circular distribution in circular statistics. It plays as central role as the Normal distribution does in usual ‘linear’ statistics. The probability density for a CND
 denoted by CND($\mu ,\kappa$), is:

$\frac{1}{2\pi I_0\left(k\right)}\exp \left(\kappa \cos \left(\alpha -\mu \right)\right),0\le \alpha <2\pi$        (1)

The mean direction is also referred to as the preferred direction and the concentration parameter can be thought of as the inverse of variance as it is a measure of concentration around the mean direction. A larger value for implies that observations are more concentrated around the mean direction, while a value of close to 0 implies there may not be a strongly preferred direction. We consider now the maximum likelihood estimates (MLEs) for the parameter in a classical and Bayesian setting.

Maximum likelihood estimate for concentration parameter

Given a random sample ${\alpha }_1,\mathrm{...},{\alpha }_n$ from a CND($\mu ,\kappa$), the MLE for $\kappa$ when $\mu$ in unknown is given by Jammalamadaka SR:⁹

$\hat{K} MLE is the solution to: \frac{1}{n}\sum _{i=1}^n\cos \left({\alpha }_{i -\overline{{\alpha }_0}}\right) =\frac{I_{1\left(k\right)}}{I_{0\left(k\right)}}$   (2)

When the mean direction $\mu$ is known, then the MLE for $\kappa$ is obtained by substituting $\mu$ in place of ${\overline{\alpha }}_0$ in 2. Since the estimation of concentration parameter is of main interest here, we will denote ˆκMLE  and ˆκµ   the MLEs for $\kappa$ when sample mean direction is used (if $\mu$ unknown), and when the mean direction $\mu$ is known, respectively. In both cases the MLEs carry the usual asymptotic properties. Analogous to the case of a linear Normal distribution, ${\hat{\kappa }}_{\mu }$ is superior (has smaller MSE) than ${\hat{\kappa }}_{MLE}$,⁹

If the sample comes from a population with population mean µ then the &$MSE\left({\hat{\kappa }}_{\mu }\right)<MSE\left({\hat{\kappa }}_{MLE}\right)$:⁹

$\frac{1}{n(1-{\overline{V}}_0/{\hat{k}}_{\mu }-{\overline{V}}^2} \le \frac{1}{n(1-\overline{R}/\hat{k}MLE-{\overline{R}}^2)}$     (3)

where we have inequality if and only if $\mu ={\overline{\alpha }}_0$. We denote $\overline{R}=\raisebox{1ex}{$R$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$ and ${\overline{V}}_o=\raisebox{1ex}{$V_o$}\!\left/ \!\raisebox{-1ex}{$n$}\right.$, where $V_o=\sum _{i=1}^n\cos \left({\alpha }_i-\mu \right)$, $R=\sum _{i=1}^n\cos \left({\alpha }_i-{\overline{\alpha }}_o\right)$, and $V_o\le R$.

 This raises the question whether we can go somewhere in between if we have partial information on µ.

MLE for when there is a prior on 

In this semi-Bayesian setting we will place a prior on the nuisance mean direction, a convenient choice being a CN:

$\pi \left(\mu \right) \frac{1}{2\pi I_0\left(\tau \right)} exp (\tau cos(\mu -{\mu }_{0)}), 0 \le \mu < 2\pi$     

where ${\mu }_o$ and $\tau$ are the mean direction and concentration parameters for the prior. The value for $\tau$ measures confidence in the prior mean direction ${\mu }_o$. A larger value of τ makes the prior distribution have higher concentration around µ₀. A value of $\tau =0$ implies a uniform prior on $[0,2\pi )$ for µ.

In this context, the parameter $\mu$ has a prior distribution, while the parameter is an unknown parameter $\kappa$ as in the classical setting. The parameter κ is of interest, while µ is the nuisance parameter. We thus blend together classical and Bayesian methods to get an estimate for κ.

We begin with the usual likelihood given the data (${\alpha }_1,\mathrm{...},{\alpha }_n$) independent and identically distributed:

$L(\mu , k/\underset{~}{\alpha }) = \left(\frac{1}{2\pi I_0\left(k\right)}\right) \exp \left(k\sum _{i=1}^n\cos ({\alpha }_{i -\mu )}\right) , 0 \le {\alpha }_i < 2\pi$      (5)

Given the prior distribution on, we wish to estimate the concentration parameter κ. We derive the likelihood function for κ by first averaging out our prior knowledge on $\mu$. The result is the likelihood for κ given by:

$\underset{0}{\overset{2\pi }{\int }}L (\mu , k| {\alpha }_1, \mathrm{...}, {\alpha }_n) \pi \left(\mu \right)d\mu = L \left(k\right| {\alpha }_1,\mathrm{...},{\alpha }_n)$         (6)

In 6, we begin with joint likelihood $L\left(K\left|{\alpha }_1,\mathrm{...},{\alpha }_n\right.\right)$ for $\kappa$ the µ and κ which is just the joint density of the data. We then derive marginal distribution for the observations by integrating with respect to µ. After incorporating our prior knowledge on µ and integrating with respect to $\mu$, we obtain   a  valid   likelihood $L\left(K\left|{\alpha }_1,\mathrm{...},{\alpha }_n\right.\right)$ for $\kappa$ which we want to maximize with respect to.

$\begin{array}{l}\underset{0}{\overset{2\pi }{\int }}L (\mu , k| {\alpha }_1, \mathrm{...}, {\alpha }_n) \\ =\underset{0}{\overset{2\pi }{\int }}\frac{\exp \left(\right|k(\Sigma \cos ({\alpha }_i) \cos (\mu ) +\Sigma \sin ({\alpha }_i) \sin (\mu \left)\right)+\cos \left(\mu \right)\tau \cos \left({\mu }_0\right) + \sin \left(\mu \right)\sin \left({\mu }_0\right))}{{\left(2\pi \right)}^n{\left(I_0\right(k\left)\right)}^{n}2\pi I_0\left(\tau \right)}d\mu \\ where setting \Sigma \cos \left({\alpha }_i\right) = R\cos \left(\overline{\alpha }\right) and \Sigma \sin \left(\alpha i\right) =| R\sin (\tilde{\alpha }) in7gives\end{array}$ (7)

$=\underset{0}{\overset{2\pi }{\int }}\frac{\exp \left(\right(kR\cos \left(\overline{\alpha }\right) +\tau \cos \left({\mu }_{{}_0}\right)) \cos (\mu )+KR\sin (\overline{\alpha }) ) + \tau \sin \left({\mu }_0\right)\left)\sin \right(\mu \left)\right)}{{\left(2\pi \right)}^n{\left(I_0\right(k\left)\right)}^{n}2\pi I_0\left(\tau \right)}d\mu$    (8)

Putting $\kappa R\cos \left(\overline{\alpha }\right)+\tau \cos \left({\mu }_0\right)=\gamma \cos \left({\alpha }^{*}\right)$ and $\kappa R\sin \left(\overline{\alpha }\right)+\tau \sin \left({\mu }_0\right)=\gamma \sin \left({\alpha }^{*}\right)$, and by the definition of the Bessel function$I_o\left(X\right)$ , the resulting integral in 8 is our likelihood for which is given by:

$L( k| {\alpha }_1, \mathrm{...}, {\alpha }_n) = \frac{2\pi I_0\left({\sqrt{k^2{R}^2+2kRT\cos ({\overline{\alpha }}_0-\mu }}_0\right)}{{\left(2\pi \right)}^n{\left(I_0\right(k\left)\right)}^{n}2\pi I_0\left(\tau \right)}$     (9).

The likelihood is a ratio of Bessel functions. Given the likelihood, prior distribution on $\mu$, and data we can find the MLE for $\kappa$. There is not a simple analytical solution for the MLE, so numerical methods are required for the maximization of 9 with respect to κ leading to the semi-Bayesian MLE ${\hat{\kappa }}_{\text{Bay}}$.

One interesting comparison would be of the frequentist MLE for κ as in 2 with the semi-Bayesian MLE obtained from 9, using a circular uniform prior distribution on$\mu$ in the latter, i.e. setting $\tau =0$. In some cases, placing uniform priors result in Bayes estimates that are similar to classical MLEs. Using a circular uniform prior distribution on $\mu$ in 9, we derive the Fisher Information to find the variance of our semi-Bayesian MLE. From 9, with a circular uniform prior, the log-likelihood is,

$\mathcal{l}=\ln I_0\left(\kappa R\right)-n\ln 2\pi -n\ln I_0\left(\kappa \right),$   (10)

and the semi-Bayesian MLE for κ is the solution to setting $\dot{\mathcal{l}}=0$ where $\dot{\mathcal{l}}=\frac{\delta \mathcal{l}}{\delta \kappa }$,

$\dot{\mathcal{l}}=R\frac{I_1\left(\kappa R\right)}{I_0\left(\kappa R\right)}-n\frac{I_1\left(\kappa \right)}{I_0\left(\kappa \right)}$    (11)

The solution for MLE in this case is found by,

${\stackrel{⌢}{k}}_{Bay}isthesolutionto:\frac{R}{n}=\frac{A\left(k\right)}{A\left(kR\right)}$      (12)

Immediately we notice a difference when comparing ${\hat{\kappa }}_{\text{MLE}}$ in 2. Taking another derivative of 11 we have obtained the Hessian where $\ddot{\mathcal{l}}=\frac{{\partial }^2\mathcal{l}}{\partial {\kappa }^2}$,

$\ddot{\mathcal{l}}=R^2\frac{{\displaystyle I_0\left(\kappa R\right)I_2\left(\kappa R\right)-I_1^2\left(\kappa R\right)}}{{\displaystyle I_0^2\left(\kappa R\right)}}+n\frac{{\displaystyle I_1^2\left(\kappa \right)-I_0\left(\kappa \right)I_2\left(\kappa \right)}}{{\displaystyle I_0^2\left(\kappa \right)}}$   

$=R^2\left(\frac{I_2\left(\kappa \right)}{I_0\left(\kappa \right)}-A^2\left(\kappa R\right)\right)+n\left(A^2\left(\kappa \right)-\frac{I_2\left(\kappa \right)}{I_0\left(\kappa \right)}\right)$   

$=\frac{I_2\left(\kappa \right)}{I_0\left(\kappa \right)}(R^2-n)+n{A}^2\left(\kappa \right)-R^2{A}^2\left(\kappa R\right)$   (13-15)

Then the Fisher Information (I) is given by,

$I=\frac{I_2\left(k\right)}{I_0\left(k\right)}(n-R^2)-n{A}^2\left(k\right)+R^2{A}^2\left(kR\right)$     (16)             

where substituting the semi-Bayes MLE, the asymptotic variance (V ) of: ${\hat{\kappa }}_{\text{Bay}}$

$V={\left(\frac{I_2\left({\hat{\kappa }}_{\text{Bay}}\right)}{I_0\left({\hat{\kappa }}_{\text{Bay}}\right)}(R^2-n)+n{A}^2\left({\hat{\kappa }}_{\text{Bay}}\right)-R^2{A}^2\left({\hat{\kappa }}_{\text{Bay}}R\right)\right)}^{-1}$    (17)

Therefore the asymptotic variance of the MLE can be found using 17. Next, we can compare the two MLE’s via their respective large-sample confidence intervals. The $(1-\gamma )\times 100\%$ confidence interval for is given by,

$\begin{array}{l}\left({\stackrel{⌢}{k}}_{MLE}\underset{\_}{+}{Z}_{(\gamma /2)\sqrt{\frac{1}{n(1-\overline{R}/{\stackrel{⌢}{k}}_{MLE}-{\overline{R}}^2)}}}\right)\\ \left({\stackrel{⌢}{k}}_{Bay}\underset{\_}{+}Z(\gamma /2)\sqrt{\left(\frac{I_2\left({\stackrel{⌢}{k}}_{Bay}\right)}{{I_0}^{\left({\stackrel{⌢}{k}}_{Bay}\right)}}\right)(R^2-n)+n{A}^2{\stackrel{⌢}{k}}_{Bay})-R^2{A}^2({\stackrel{⌢}{k}}_{Bay}R){}^{-1}}\right)\end{array}$

Figure 1 displays histograms for ${\hat{\kappa }}_{\text{MLE}}$ and ${\hat{\kappa }}_{\text{Bay}}$ based on 1000 simulations from the CND with $\kappa =1,3$, using sample size of $n=30$. In each $\kappa$ setting the histograms of estimated values are nearly identical for ${\hat{\kappa }}_{\text{MLE}}$ and.${\hat{\kappa }}_{\text{Bay}}$

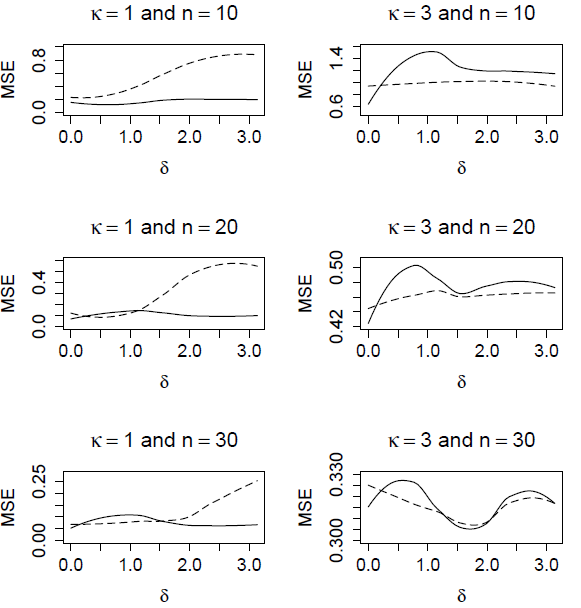
Figure 1 Histograms of ${\hat{\kappa }}_{\text{MLE}}$(MLE) and ${\hat{\kappa }}_{\text{Bay}}$(Bayes) with circular uniform prior for 1000 simulations from CND(µ,κ).

Preliminary test estimators

A preliminary test estimator (PTE) is a method of estimation that introduces sample-based prior information via a hypothesis test on the nuisance parameter to aid in estimating the parameter of interest.¹ If we fail to reject the null, then we use an estimator evaluated using the null hypothesis value. If we reject the null hypothesis, we use an estimator based directly on the sample, the usual MLE. The parameter value in the null hypothesis represents our prior knowledge. The idea is when the true parameter value is in or near the null hypothesis value, the PTE will provide a better estimator in terms of mean squared error (MSE), or any other risk function.

We observe data from a CND with unknown mean direction and concentration parameter. We are interested in estimating the concentration parameter, with the mean direction being a nuisance parameter. Our preliminary test has null hypothesis of mean direction equal to a pre-specified direction, versus a two-sided alternative.

Our PTE for the concentration performs better than the usual MLE and Bayesian estimates for the parameter. The result is similar to the linear case where we have a normal distribution with unknown mean and variance.¹⁰ This methodology can be used to improve the estimation accuracy in many existing applications since the CND is one of the most commonly used distributions in circular statistics.

Test for assumed mean direction

Suppose we have observations ${\alpha }_1,\mathrm{...},{\alpha }_n$from a CND with both mean direction and concentration parameter unknown. We want to test:

$H_0:\mu ={\mu }_{0}vs{H}_1:\mu \ne {\mu }_0$ (18)

In the linear case with data from a Normal distribution, this is parallel to the standard Student’s t-test. In,⁹ the Likelihood Ratio Test (LRT) is based on the test statistic:

$V_0=\sum _{i=1}^n\cos ({\alpha }_i-{\mu }_0)or\frac{V_0}{R}=Cos({\overline{\alpha }}_0-{\mu }_0)$ (19)

where we reject the null hypothesis for small values of the test statistic. Note the distribution for $V_0$ and $\frac{V_0}{R}$ depend on the nuisance parameter $\kappa$. However, the exact conditional test for the mean direction of the CN can be obtained by using the conditional distribution of $R|V_0$, which is independent of$\kappa$. $V_0$ is the length of the projection of sample resultant vector, $R$, towards the null hypothesized mean direction, ${\mu }_0=\left(\cos \left({\mu }_0\right),\sin \left({\mu }_0\right)\right)$. In the conditional test we reject null if $V_0$ is too small for a given $R$, or equivalently, we reject the null if $R$is too large for a given $V_0$.

To illustrate the geometry of the test, suppose we have polar vector given by the null hypothesis, $\left(\cos \left({\mu }_0\right),\sin \left({\mu }_0\right)\right)$. Next, we have n observations and we calculate the length of projection,$c$, of the sample resultant vector on the polar vector. Conditioning on the value of $c$, we find the probability of observing our sample resultant vector, $R$, and larger values when the null direction is true, conditional on the observed value of $V_0=V$.

The space consists of sample resultant vectors that have projection length, c, on the polar vector. Suppose$R_1$ and $R_2$ are two resultant vector with equal projection length and $R_1>R_2$. Then the direction of $R_1$ is further away from ${\mu }_o$, than $R_2$’s direction.

For significance level $\gamma$, we find the rejection region via the exact conditional distribution of $R|V_0$. That is, $r_0$ is the solution to the equation that satisfies:

$P(R>r_0|V_0=v)=\gamma$ (20)

As shown in [9], this critical point $r_0$ is the solution to:

$\underset{r_o}{\overset{n}{\int }}f\left(r\right|v)dr=\underset{r_o}{\overset{n}{\int }}\frac{r{\psi }_n\left(r\right)}{\sqrt{r^2-v^2{f}_0\left(v\right)\pi }}dr=\alpha$ (21)

where we solve for $r_0$, for a given $v$ and $n$. Equations for ${\Psi }_n\left(r\right)$and $f_0\left(v\right)$ can be found in.⁹ There is no analytical solution for $r_0$ in this case, and¹¹ provides a table of rejection regions for various values of $v_0$ . To simplify our hypothesis test we use results in,¹² where approximate confidence intervals for the mean direction are provided. Our test statistic derived from the approximate LRT is broken into two cases:

For $\overline{R}\le 0.9$ , we reject $H_0$ if: 

$R_2>V_0^2+\frac{1}{4n}(2n^2-V_0^2)Z_{\gamma }$      (22) 

Where $\overline{R}=\frac{R}{n}$ and $Z_{\gamma }$ is the upper quantile of the standard Normal distribution.

For $\overline{R}\ge 0.9$ , we reject $H_0$ if:

$n\log \left(\frac{n^2-V_0^2}{n^2-R^2}\right)>X_{1,\gamma }^2$ (23)       

These approximations hold well for even small sample sizes when the concentration is high.

The PTE for the concentration parameter
Now we introduce our PTE for estimating the concentration parameter, where the mean direction is a nuisance parameter. Given observations, ${\alpha }_1,\mathrm{...},{\alpha }_n$, with unknown mean direction and concentration parameter we test our null hypothesized mean direction via the aforementioned hypothesis test. Our PTE is given by:

(i) For$\overline{R}\le 0.9$ ,

${\stackrel{⌢}{k}}_{PTE}={\stackrel{⌢}{k}}_{MLE}\parallel \left(Z\right|>Z_{\gamma })+{\stackrel{⌢}{k}}_{\mu o}\parallel (Z<Z_{\gamma })$ (24)        

where $Z$ is found by using 22 and solving for $Z_{\gamma }$.

(ii) For $\overline{R}\ge 0.9$,

${\stackrel{⌢}{k}}_{PTE}={\stackrel{⌢}{k}}_{MLE}\parallel (X^2>{X^2}_{1,\gamma })+{\stackrel{⌢}{k}}_{\mu o}\parallel (X^2>{X^2}_{\gamma ,r})$                        (25)

where χ2 is found by using 23.

we break the estimator into the two cases according to our hypothesis test. The PTE in either case selects only one of the two estimators according to the result of the hypothesis test. The performance of the PTE depends on the level of the test and the proximity of the true mean direction to the null hypothesized value. We measure performance in terms of mean squared error (MSE) of our estimator over different significance levels γ, and different true differences between the mean directions $\delta =\mu -{\mu }_0$.

In Figure 2, we observe the simulation-based MSE of the PTE and MLE for the concentration parameter. We perform 1000 simulations of $\left({\alpha }_1,\mathrm{...},{\alpha }_{20}\right)~CN\left({\delta }_j,\kappa \right),$ for $j=1,\mathrm{...},50$. Here ${\delta }_1,\mathrm{...},{\delta }_{50}$ represent the 50 equally spaced points between 0 and π. For each ${\delta }_j$, we record the MSE. Each line represents MSE of an estimator over values of $\delta =\mu -{\mu }_0$, where $\delta$represents the true difference between the population mean direction and the null hypothesized mean direction.

Figure 2 Simulation-based MSE of MLE and PTE for different significance levels $\gamma$ .

For significance levels $\gamma =.10,.15,.25,$the PTE performs at least as good as the MLE, and performs better when the true mean direction is closer to the null hypothesized value. For larger significance levels the test requires less evidence to reject the null hypothesis, and when we reject the null the PTE is equivalent to the MLE, ${\hat{\kappa }}_{\text{MLE}}$. In Figure 2, we observe that as the significance level increases the PTE is more likely to use ${\hat{\kappa }}_{\text{MLE}}$ for smaller values of$\delta$ . To show the vast improvement in our PTE, we examine the mean-square relative efficiency (MRE) of the 2 estimators

PTE and MLE, defined by

$e({\stackrel{⌢}{k}}_{PTE}={\stackrel{⌢}{k}}_{MLE})=\frac{MSE\left({\stackrel{⌢}{k}}_{MLE}\right)}{MSE\left({\stackrel{⌢}{k}}_{PTE}\right)}$ (26)

Values larger than unity imply that the PTE performs better than the MLE. In Figure 3, we have the MRE of the MLE and PTE with $\gamma =0.01$ across all values of $\delta$ . The relative efficiency is greater than 1 for all $\delta$ less than approximately 0.65 radians. In this example, the PTE can reduce the MSE by 20% when the true difference in mean directions is small. For.$65<\delta <1.5$, the MRE is less than 1 implying the MLE has the smaller MLE. This is due to our preliminary test failing to reject the null hypothesis. For $\delta >1.5$, the preliminary test will almost always reject the null hypothesis value and the PTE will be the same as the MLE resulting in the MRE being equal to one.

Figure 3 Mean-squared error relative efficiency of MLE and PTE with $\gamma$= 0.01.

In Equation 3, the MRE is maximum for $\delta =0$, and when the PTE will almost always reject the null for large enough $\delta$ the MRE is equal to one. For $0<\delta <\pi$ the PTE may reject or fail to reject the null hypothesis depending on the sample observed. In the case it fails to reject, $V_0={\sum }_{i=1}^n\cos \left({\alpha }_i-{\mu }_0\right)$ is no longer minimized at ${\mu }_0$µ0 since $\mu$ is the population mean (Recall $\delta =\mu -{\mu }_0$). Therefore $V_0<R$ if ${\mu }_0$ is closer to $\mu$than $¯{\alpha }_0$, and $V_0>R$ if $¯{\alpha }_0$ is closer to $\mu$ than ${\mu }_0$. If the latter case appears more often than the former case for some intermediate values of $\delta$ , then the MRE will be less than 1.

In Figure 2, we compare the MLE and PTE with $\gamma =0.01$ from Figure 2 .The PTE with $\gamma =0.01$has the best results for smaller values of $\delta$ , but could perform worse than the MLE for intermediate values of $\delta$ . PTEs with $\gamma =0.1,0.15,0.25$ perform at least as good as the MLE. Now, we illustrate other possibilities that can occur and the performance of the PTE.

In Figure 4, we simulate from four different realities and examine the performance of our PTE for the same significance levels as used in Figure 2. Note that the lines have same labels as in Figure 2. For each plot we have simulated-based MSEs for each line. We perform 1000 simulations of $\left({\alpha }_1,\mathrm{...},{\alpha }_n\right)~CN\left({\delta }_j,\kappa \right)$, for $j=1,\mathrm{...},50.$Here ${\delta }_1,\mathrm{...},{\delta }_{50}$ represent the 50 equally spaced points between 0 and π. For each δj, we record the MSE which creates our MSE curve over $\delta$ for each scenario.

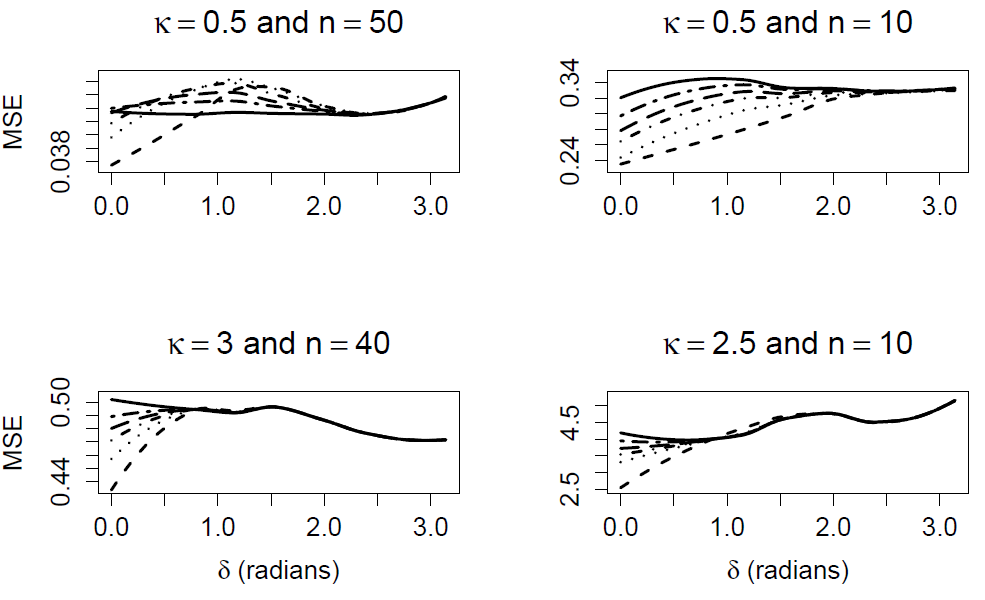
Figure 4 Simulation-based comparison of PTE performances for sample sizes $n=10,40,50$ and concentration parameters $\kappa \in \left\{0.5,2.5,3\right\}$ . lines are labeled as in Figure 2.

First examine that in all scenarios, the PTE with significance level γ = 0.01 performs the best when the true difference in mean direction is null or small. In the top-left plot we have n = 50 simulated observations from CN(δ,κ = 0.5); top-right plot we have n = 10 simulated observations from CN(δ,κ = 0.5); bottom-left plot we have n = 40 simulated observations from CN(δ,κ = 3); bottom-right plot we have n = 10 simulated observations from CN(δ,κ = 2.5).

In the top-right plot all of the PTE’s in this simulation performed uniformly better (over $\delta$ ) than ˆκMLE. In the remaining three plots there are values of $\delta$ where the ˆκMLE has better performance. This occurs when our preliminary test fails to reject the null hypothesis for intermediate values of $\delta$ . The difference becomes more obvious when we have a large sample size and the value of κ is small as in the top left plot. Here the PTE’s MSE increases for intermediate values of $\delta$ , for relatively smaller significance levels. There is a similar pattern in the bottom two plots. This pattern is to be expected, since smaller significance level will require more evidence to reject the null hypothesis of the preliminary test.

In applications, the values of $\delta$ and κ are unknown. So how do we select the optimal significance level given n observations from $CN\left(\mu ,\kappa \right)$? Following the work of,¹ we create tables to find a PTE with minimum and maximum MREs.

Tables were constructed through simulations. Given a sample size n and value for κ, we generate values from a CN(δ,κ) distribution to estimate the MRE over a grid of γ and $\delta$ values, where 0 ≤ δ ≤ π. For each γ, we compute the maximum MRE,

Emax, minimum MRE, $E_{min}$, over all $\delta$ , and record the $\delta$ where $E_{min}$ is located, ∆min. For almost all cases the location of the maximum MRE is located at $\delta =0$ and the function MRE(δ) is monotone decreasing from $\delta =0$ to $\delta =E_{min}$. For values $\delta >E_{min}$, the function MRE($\delta$) increases back to unity since the PTE will reject the null hypothesized values for larger $\delta$ . We then repeated this procedure for different parameter values for κ.

The mean resultant vector is the normalized length of R since 0 < R <¯ 1 and is a measure of concentration for a sample of observations. A value close to 1 implies high concentration and a value close to 0 implies little to no concentration around any single direction. This estimate does not depend on the knowledge of κ or of the mean $\mu$ of the distribution. For the CND, there is a one-to-one correspondence between statistic $R¯$ and the concentration parameter κ. Given a sample size n and κ, we observe the average $R¯$ over our simulations and use the average as an indication of strength of concentration. In practice, we advise the user to find the sample observed $R¯$ of the n observations, and then use the column of the table with the nearest $R¯$ value.

In Table 1, we provide a list of potential PTEs for n = 20. The rows list various significance levels γ for the PTE ranging from 1% to 50%. The columns list the different observed values for $R¯$. Suppose we have a sample size of 20 observations and observe $R¯$ close to 0.779. Following the procedure in,¹ we then decide the minimum MRE preferred is $E_{min}=0.471$. Then using the Table 1, the optimal PTE corresponds to using $\alpha =\mathrm{0.20.}$Upon request, we provide tables for various sample sizes, where the tables require only knowledge of sample size, R¯, and the predetermined $E_{min}$.

Comparison of the PTE and bayes estimators
Both the PTE and Bayes estimators in 12, use prior information on the mean direction ${\mu }_0$ to aid in estimation of the concentration parameter. A smaller significance level for the PTE requires stronger evidence to reject the null hypothesized value ${\mu }_0$. A smaller significance level may be chosen to coincide with a stronger belief in the mean direction ${\mu }_0$. In the previously mentioned Bayesian setting of this chapter, a larger value for the concentration parameter τ focuses our prior distribution around the mean direction ${\mu }_0$. A larger value in parameter τ represents a stronger belief in prior mean direction ${\mu }_0$.

In Figure 5 we make a comparison of the MSE of our PTE with significance level of 1% with the Bayes estimator with CN prior centered around the null hypothesis value ${\mu }_0$ and with $\tau =4$. We plot the MSE curve of each estimator over values of $\delta$ .

Figure 5 MSE of PTE and Bayes estimators over δ: ${\stackrel{⌢}{k}}_{PTE}\left(—\right)$and ${\hat{\kappa }}_{\text{Bay}}\left(---\right)$.

In each plot, the solid line is MSE curve for the PTE and the dashed line is the MSE curve for the Bayes estimator. For κ = 1, $ˆ{\kappa }_{PTE}$ performs better overall for all sample sizes. For $n=10$, $ˆ{\kappa }_{PTE}$ performs uniformly better than ${\hat{\kappa }}_{\text{Bay}}$. For $n=20$ and $n=30$ the estimators have similar performances for small values of $\delta$, but the MSE for ${\hat{\kappa }}_{\text{Bay}}$ is much larger for large values of $\delta$ .

If κ = 3, we have different results when comparing the MSEs. In all sample sizes of $n=10,20,30,$ the MSE of $ˆ{\kappa }_{PTE}$ is best for small values of $\delta$ . Also, for all sample sizes, ${\hat{\kappa }}_{\text{Bay}}$ has the smaller MSE for the larger values of $\delta$ . In this case for large value of κ, ${\hat{\kappa }}_{\text{Bay}}$ would be the preferred estimator since the performance is better overall.

In reality we do not know the value of κ, so need a data driven way to select ${\hat{\kappa }}_{\text{Bay}}$ versus $ˆ{\kappa }_{PTE}$. If we suspect a high concentration then we suggest to use ${\hat{\kappa }}_{\text{Bay}}$, and for a weak concentration then use $ˆ{\kappa }_{PTE}$. If given a sample size n, go to the corresponding PTE table for the same sample size. In the table, go to the 7th column which gives the expected $R¯$under $\kappa =3$ simulations. From your observed sample of size n, calculate R¯ in column 7, and compare to the value from the PTE table. If less than the PTE table value, then use $ˆ{\kappa }_{PTE}$, otherwise use ${\hat{\kappa }}_{\text{Bay}}$.

In our work we have shown a superior estimator for the concentration parameter when the mean direction is unknown of a CND. In all cases the PTE has better performance in terms of MSE if $\delta$is null or small. Another interesting result is in comparison for the PTE we developed an MLE for the concentration parameter based from the prior distribution of mean direction.

None.

Authors declare that there are no conflicts of interests.

1. Saleh AME. Theory of preliminary test and Stein‒type estimation with applications. volume 517. John Wiley & Sons. 2006;pp. 656.
2. Bancroft TA. On biases in estimation due to the use of preliminary tests of significance. The Annals of Mathematical Statistics. 15(2):190‒204.
3. Bancroft TA. Analysis and inference for incompletely specified models involving the use of preliminary test (s) of significance. Biometrics. 1964;20(3): 427‒442.
4. Bancroft TA. Inference for incompletely specified models in physical sciences. Bulletin of the International Statistical Institue. 1965;41(1):497‒515.
5. Snedecor GW. Statistical Methods. Collegiate Press, Iowa, USA. 1938.
6. Han C, Bancroft TA. On pooling means when variance is unknown. Journal of the American Statistical Association. 1968;63(324):333‒1342.
7. Stein C. Inadmissibility of the usual estimator for the mean of a multivariate normal distribution. In: Proceedings of the Third Berkeley symposium on mathematical statistics and probability, University of California Press, Berkeley, USA, volume 1. 1956;pp. 197‒206.
8. James W, Stein C. Estimation with quadratic loss. In Proceedings of the fourth Berkeley symposium on mathematical statistics and probability. 1961;1:361‒379.
9. Jammalamadaka SR, SenGupta A. Topics in circular statistics. volume 5. World Scientific, Singapore. 2001.
10. Ohtani K. Estimation of the variance in a normal population after the one‒sided pretest for the mean. Communications in statistics‒theory and methods. 1991;20(1):219‒234.
11. Stephens MA. Exact and approximate tests for directions. Biometrika. 1962;49(3‒4):463‒477.
12. Upton GJG. Approximate confidence intervals for the mean direction of a von mises distribution. Biometrika. 1986;73(2): 525‒527.