In this paper, an attribute control chart is aimed when the lifetime of the item follows Type-II generalized log-logistic distribution (TGLLD) under a time truncated life test assuming that the common scale parameter is known. Average run length (ARL) is used to assess the performance of the aimed control chart. Simulation technique is developed to present the performance of the control charts at a specified average run length (ARL), shift constant and for different parametric values of shape and scale parameters, sample size. The results are illustrated with live data example.

Keywords: Type-II generalized log-logistic distribution, attribute control chart, life test, average run length

Control charts are popularly known to be tools for assessing the quality of the item. In general, the aim of the manufacturer is to produce the items to meet the specified quality standards. Today’s competitive world has emphasized manufacturers to improve and sustain with the quality standards that are essential to stable their position in the business. This will necessitate to have quality checks at regular intervals. This can be achieved by placing the technique of control charts as a process monitoring system. With the diverged growth in industrial sector, control charts find its applicability largely in the manufacturing and as well in other industries due to ease in implementation and to arrive a quick conclusion on the process status whether it is within the control limits. In general, the two control limits of the control chart known as upper control limit (UCL) and lower control limit (LCL) are treated as the boundaries for the quality specifications of the item. If the statistic under consideration falls within the control limits, then the process is said to be a controlled one, otherwise the process is treated as out of control. Items for which the quality specification i.e., statistic under consideration falls beyond the control limits are called as non-conforming. Control chart technique is useful to meliorate the lineament of the item to reduce non-conforming items which in turn give benefit to the manufacturer in terms of production cost and reputation of the item produced.

There are two types of control charts viz. variable control charts and attribute control charts. If the data on quality measurement is readily available, then variable control charts will provide well predicted results on the item quality, on the other hand attribute control charts are to be considered for isolating non-conforming items from conforming items. Different authors have paid their attention to develop the control chart techniques for various distributions, for use of reference few of such plans are Amin et al.,¹ Bai and Choi,² Al-Orani and Rahim,³ Wu et. Al.,⁴ Wu and Wang,⁵ Lin and Chou,⁶ Zandi et. Al.,⁷ McCracken and Chakraborti,⁸ Joekes and Barbosa,⁹ Azam et al.¹⁰ and Aslam et. al.,¹¹ Rao GS,¹² Rao et al.,¹³ Adeoti and Ogundipe.¹⁴

The motive behind this study is to formulate an attribute control charts for process monitoring when the lifespan of an item produced follows Type-II generalized log-logistic distribution (TGLLD). As we know, the ARL is the average number of points that must be plotted before a point indicates as disorderly condition. If the process observations are uncorrelated, then for any Shewart control chart, the ARL can be computed as

$ARL=\frac{1}{p}$ ,

where p is the probability that any point outdoes the control limits. This equation can be used to assess the functioning process of the control chart. Wu and Jiao,¹⁵ Wu et. Al.¹⁶ and Ho and Costa^17,18 have contributed in some developments of this area. The leftover portion of the article is prepared in the succeeding direction. Introduction of TGLLD is given in Section 2. In section 3, the plan of aimed control charts under a time truncated life test are given for this distribution. In Section 4, simulation study with illustrative examples is demonstrated. Finally, inferences made under this plan are given in Section 5.

The ease in adaptability and broad applicability made Log-logistic distribution (LLD) to find its own importance in quality control. Different types of acceptance sampling plans are developed for LLD. The cumulative distribution function (cdf) of the log-logistic distribution (LLD) is

$F\left(t;\sigma ,\theta \right)=\frac{{{\displaystyle \left(\frac{t}{\sigma }\right)}}^{\lambda }}{\left[1+{{\displaystyle \left(\frac{t}{\sigma }\right)}}^{\lambda }\right]};t>0,\sigma >0,\lambda >1$ (1)

As described above, the practical adaptiveness of generalized log-logistic distribution (GLLD) in diverse sectors, various authors have paid their attention in developing different types of acceptance sampling plans when the lifetime variate follows GLLD. An extended version to this distribution named as Type-II generalized log-logistic distribution (TGLLD) introduced by Rosaiah et al.,¹⁹ its cumulative distribution function (cdf) is

$F(t;\sigma ,\theta ,\lambda )=1-{{\displaystyle \left[1+{{\displaystyle \left(\frac{t}{\sigma }\right)}}^{\lambda }\right]}}^{-\theta };t>0,\sigma ,\theta >0,\lambda >1$ (2) 

We state that the distribution given in (2) is defined through the reliability-oriented generalization of log-logistic distribution. In simple words, this can be called as the Type-II generalized log-logistic distribution [Type-I generalized (exponentiated) log-logistic distribution is dealt with by Rosaiah et al. (2006)]. The associated probability density function (pdf) is given by

  $f(t;\sigma ,\theta ,\lambda )=\frac{\lambda \theta }{\sigma }\frac{{{\displaystyle \left(\frac{t}{\sigma }\right)}}^{\lambda -1}}{{{\displaystyle \left[1+{{\displaystyle \left(\frac{t}{\sigma }\right)}}^{\lambda }\right]}}^{\theta +1}};t>0,\sigma ,\theta >0,\lambda >1$ (3)         

where σ is the scale parameter, λ and θ are shape parameters. The average life of the TGLLD is$\mu =\sigma \eta$

, where $\eta ={\left[{\left(0.5\right)}^{-1/\theta }-1\right]}^{1/\lambda }$ .                                                                                                   (4)

The following procedure is adopted for constructing a control chart based on the number of non-conforming (also called np control chart) under time truncated life test. We prefer to use average as the quality parameter, and it is denoted by $\eta ={\left[{\left(0.5\right)}^{-1/\theta }-1\right]}^{1/\lambda }$ .

Step1: Consider a sample of n items at random from each output lot and run a time truncated life test process on each item. Let D be the items conked-out within the test termination time t₀ expressed as $t_0=a{\mu }_0$ , where a is constant associated with targeted average life ${\mu }_0$ when the process is assumed to be under control..

Step 2: Treat the process is under control if D lies between LCL and UCL; otherwise the process is to be treated as out of control.

Obviously, D is a binomial variate with parameters n and p, hence the control limits of the aimed production process is given by

$UCL=n{p}_0+k\sqrt{n{p}_0\left(1-p_0\right)}$ (5a)      

$LCL=\max \left[0,n{p}_0-k\sqrt{n{p}_0\left(1-p_0\right)}\right]$ (5b)

where $p_0$ is the probability that an item is conked-out ahead of the test termination time t₀ and it is obtained from (2) as $p_0=F({{\displaystyle t}}_0)$ and k is the constant to be derived. We prefer to use average as the quality parameter and $\mu$ it is denoted by and a better practice is to set the termination time as multiple of the targeted average lifetime,$a\eta$ then $p_0$ can be rewritten as

$p_0=1-{{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}$ where ${\eta }_0={\left[{\left(0.5\right)}^{-1/\theta }-1\right]}^{1/\lambda }$

In an actual scenario, probability $p_0$ is unknown; thus, for the pragmatic execution, the control limits are set as

$UCL=\overline{D}+k\sqrt{\overline{D}\left(1-\overline{D}/n\right)}$ (7a)

$LCL=\max \left[0,\overline{D}-k\sqrt{\overline{D}\left(1-\overline{D}/n\right)}\right]$ (7b)

where $\overline{D}$ is the average number of conked-out items over the subpopulations.

The values of the parameters LCL, UCL and n are to be determined in such a way that out-of-control average run length (called ARL₁) is minimized, subject to a fixed under-control average run length (called ARL₀). The probability that the directed process to be declared as under control is

${{\displaystyle p}}_{\left[in\right]}^0=P\{LCL\le D\le UCL|p\}={\displaystyle \sum _{d=[LCL]+1}^{[UCL]}\left(\begin{array}{c}n\\ d\end{array}\right)}{\left(1-{{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}\right)}^d{\left({{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}\right)}^{n-d}$ (8)

The ARL for controlled process is given as

$AR{L}_0=\frac{1}{1-{\displaystyle \sum _{d=[LCL]+1}^{[UCL]}\left(\begin{array}{c}n\\ d\end{array}\right)}{\left(1-{{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}\right)}^d{\left({{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}\right)}^{n-d}}$ (9)

 ARL when Scale parameter is shifted

There is no change in shape and scale parameters i.e., no change in the average when the process is under control. Our interest is to determine the behavior of the production process when there are unilateral shifts in the scale parameter $\sigma$ . The process is treated as out-of-control, if there is a shift in the scale parameter i.e.${{\displaystyle \sigma }}_0$ , is replaced by ${{\displaystyle \sigma }}_1$ where ${{\displaystyle \sigma }}_1=c{{\displaystyle \sigma }}_0$ , where c can be known as shift constant.

Let ${{\displaystyle p}}_1$ be the probability that an item is conked-out ahead of the test termination time t₀, then from (2)

. ${{\displaystyle p}}_1=F({{\displaystyle t}}_0;{{\displaystyle \sigma }}_1,{\theta }_0,{\lambda }_0)=1-{{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0/c\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}$ (10)

The probability of an under-control of the shifted process is given as

${{\displaystyle p}}_{\left[in\right]}^1=P\left\{LCL\le D\le UCL/{{\displaystyle p}}_1\right\}$ $={\displaystyle \sum _{d=[LCL]+1}^{[UCL]}\left(\begin{array}{c}n\\ d\end{array}\right)}{\left(1-{{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}\right)}^d{\left({{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}\right)}^{n-d}$ . (11)

The ARL for the shifted process is given as follows.

${{\displaystyle ARL}}_1=\frac{1}{1-\left[{\displaystyle \sum _{d=[LCL]+1}^{[UCL]}\left(\begin{array}{c}n\\ d\end{array}\right)}{\left(1-{{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}\right)}^d{\left({{\displaystyle \left[1+{{\displaystyle \left(a{\eta }_0\right)}}^{{\lambda }_0}\right]}}^{-{\theta }_0}\right)}^{n-d}\right]}$ . (12)

Placed below is the procedure followed to construct the tables for the aimed control chart.

(1) Define the values of ARL named as $r_0$ , shape parameters ${\lambda }_0$ , ${\theta }_0$ and the constant a.

(2) Control chart parameter values and the size n is to be determined in such a way that given in equation (9) draw near to the specified ARL .

(3) With the help of equation (12) and according to shift constant a, determine by taking parameters of control chart derived in step 2.

We found the control chart parameters and for different valuates of ${\lambda }_0$ , ${\theta }_0$ and n and presented in Tables 1–6. Having observed the pattern of the tables, placed below are the points recorded.

1. Keeping the other parameters are fixed, when n gains the ARL numbers depicted a downward path.
2. Keeping the other parameters are fixed, when the shape parameter raises the ARL numbers flowed into downward route.
3. At fixed numbers of other parameters, The ARL figures are moves down as shift c decreases when other parameters are fixed.

 Application of aimed chart

The general motive of the manufacturer is to meliorate the quality of the manufactured items when their lifespan follows the TGLLD distribution with shape parameters ${\lambda }_0=1.5,{\theta }_0=1.5$ . Assume that the intended average life of item is 1000 hours and sample size of n=20 will be taken for each subpopulation in truncated life test experimentation. If $r_0=300$ is the set value of regimented ARL for the aimed control chart then from Table 1, we get a= 0.9347, k=2.370. From Eq. (6), the probability is derived as $p_0=0.4721$ . Using Eq. (5) the UCL and LCL numbers are found as LCL = 4.14 and UCL = 14.73. Then, the aimed control chart can be executed as given below:

Step 1: Consider 20 sample items from each subsection and set them to test their lifespan for period of 635.3 hours. Mark the conked-out items (D) during the trial process.

Step 2: The process is adjudged in-control, if 4.14 ≤ D ≤ 14.73, otherwise process is out-of- control.

The methodological analysis adopted for the aimed control chart can be exemplified with simulated data. The paces followed are placed below for yielding data points from TGLLD and building the control chart:

Step 1: Select a subpopulation of size n.

Step 2: Take a random variable X follows TGLLD of size n with scale parameter $\sigma$ =1 and shape parameters $\lambda =1.5\text{and}\theta =1.5$ .

Step 3: Determine the statistic which describes the failures count say D of each subpopulation.

Step 4: Steps 1 to 3 will be executed till the intended count of sample sets (m= 29) are achieved.

Step 5: Build the control limits LCL and UCL for the aimed chart.

Step 6: Mark all statistics D against their sample sets.

In this plan, a sample subgroup of size 29 are brought forth from TGLLD with regimented parameters $\sigma$ =1, $\lambda =1.5\text{and}\theta =1.5$ and another sample subgroup of 29 samples of size 20 are from TGLLD with parameters ${\sigma }_1=0.75$ , $\lambda =1.5\text{and}\theta =1.5$ (i.e. out-of-control process with a shift of c=0.75). It is observed from Table 1, when ARL is 370 and under control parameters, we found control chart coefficient k is 2.968 for the aimed chart at $n=20$ .

The resultant time of lifespan test will be $t_0=0.9058X0.70138=0.635315$ . For each of the subgroup the count of conked-out items D are recorded and presented in Table 7, average number of failures $\overline{D}=9.2758$ . Hence, the control limits of the aimed control chart are obtained from equation (7) and they are UCL=15.88 and LCL=2.65. Figure 1, represents the plotted points of the aimed control chart. It is observed from diagram 1, that the aimed chart displayed the shift at 32^nd observation (3^rd observation after the shift) whereas tabled ARL value is 29. Thus the aimed control chart finds more effectively to shift the process.

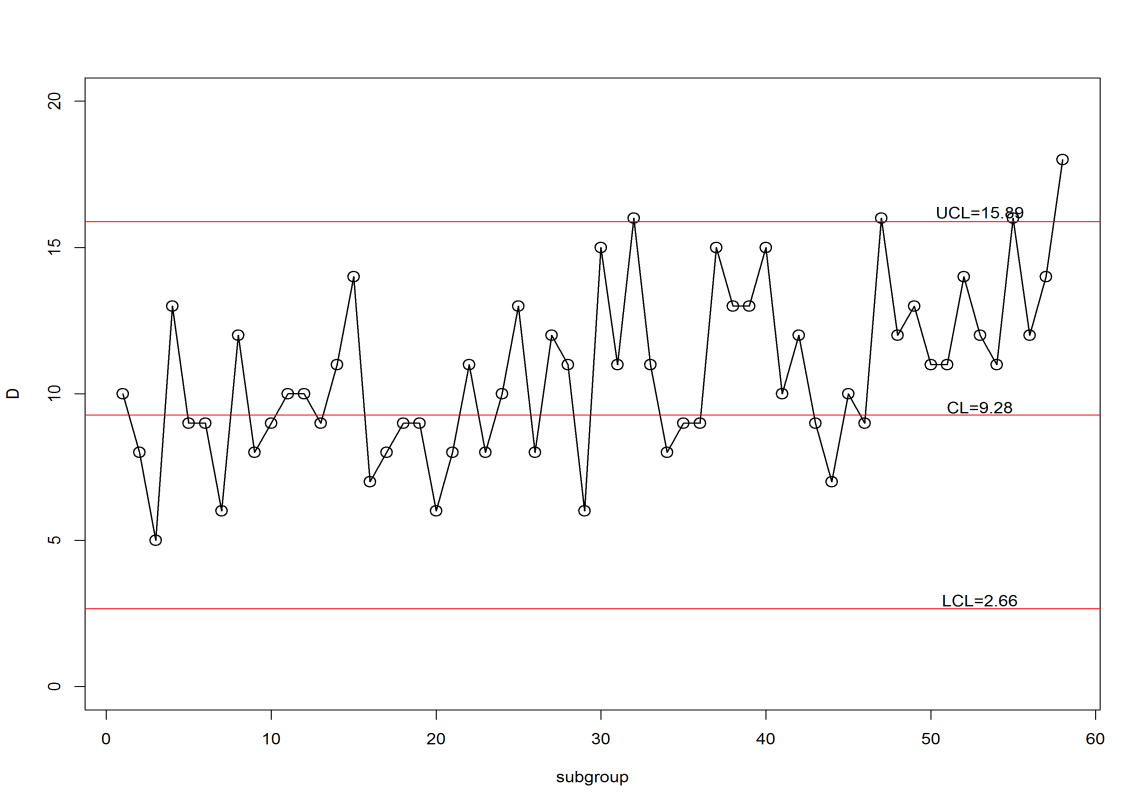
Figure 1 The graph of aimed control chart from simulated data.

This article presents, a newly attribute control chart is aimed when the lifespan of the item follows Type-II generalized log-logistic distribution (TGLLD). This chart is truly adaptable to ensure the desirable lifespan of quality items. For the actual usage, the invariable of control charts are presented for respective decisiveness parameters. The functioning of aimed chart is described in terms of ARLs according to different shift parameters. For industrial usage, the tables are exhibited and explicated clearly with the support of modelled data. It is noticed that keeping the other parameters are fixed, whenever n moving up, ARL values depicted a downward path , again when shape parameter moves up, the ARL values have flowed into downward way.

None.

None.

1. Amin R, Reynolds M R, Jr. and Bakir S.T. Nonparametric quality control charts based on the sign statistics, Commun. Statist theory methods. 1995;24:1597-1623.
2. Bai D S, Choi IS. X bar and R control charts for skewed populations, J Qual Tech. 1995;27:120‒131.
3. Al- Oraini H A, Rahim, M A. Economic statistical design of control charts for the Systems with gamma in-control times, J. Appl. Stat. 2003;30:397‒409.
4. Wu Z, Luo H,Zhang X. Optimal np control chart with curtailment, Eur J Oper Res. 2006;174(3):1723‒1741.
5. Wu Z,Wang Q. An np control chart using double inspections, J. App Stat. 2007;34(7):843‒855.
6. Lin YC, Chou CY. Non-normality and the variable parameters x bar control charts, J Oper Res Soc. 2007;176:361‒373.
7. Zandi F, NiakiSTA,Nayeri, et al. Change-point estimation of the process fraction non-conforming with a linear trend in statistical process control, J Comput Integr Manuf. 2011;24(10):939‒947.
8. McCracken AK ,Chakraborti S. Control charts for joint monitoring of mean and variance: an overview, Qual Technol Quant Manag. 2013;10(1):17‒36.
9. Joekes S,Barbosa E.P. An improved attribute control charts for monitoring non-conforming proportion in high quality processes, Control Eng Pract. 2013;21:407‒412.
10. Azam M, Aslam M,Jun CH. Designing of a hybrid exponentially weighted moving average control charts using repetitive sampling, Int.J.Adv.Manuf Technol. 2015;77:1927‒1933.
11. Aslam M, Khan N, Jun CH. A control chart for time truncated life tests using Pareto distribution of second kind. Journal of Statistical Computation and Simulation. 2016;86(11).
12. Rao GS. A control chart for time truncated life tests using exponentiated half logistic distribution. Applied Mathematics and Information Science. 2018;12(1):125–131.
13. Rao GS, Fulment AK, Josephat PK. Attribute control chart for the Dagum distribution under truncated life tests. Life Cycle Reliability Safety Engineering. 2019;8:329‒335.
14. Adeoti O A, Ogundipe P. A control chart for the generalized exponential distribution under time truncated life test. Life Cycle Reliability Safety Engineering. 2021;10(1):53‒59.
15. Wu Z, Jiao J. A control chart for monitoring process mean based on attribute inspection. International journal of Production Research. 2008;46(15):4331‒4337.
16. Wu Z, Khoo MBC, L Shu, et al. An np control chart for monitoring the mean of a variable based on an attribute inspection. Int. J. of Production Economics. 2009;121(1):141‒147.
17. Ho LL, Costa A.F.B. Monitoring a wandering mean with an np chart, Producao. 2011;21:254‒258.
18. Ho LL,Costa A.F.B. An attribute control chart for monitoring the variability of a process, Int. J. production Economics. 2013;145:263‒267.
19. Rosaiah K, Kantam R.R.L, Santosh Kumar Ch. Reliability test plans for exponentiated log-logistic distribution, Economic Quality Control. 2006;21(2):165‒175.