In modelling data related to reliability, one of the most sought out distribution is the Lindley distribution. Lindley distribution was studied by Lindley,1 with an advantage of having a single parameter, with an increasing hazard rate function (hrf). The Lindley distribution is a linear combination of the Gamma (2, β) and exponential (β) distribution.
Let Z be a random variable following the Lindley distribution with parameter β. The probability density function (pdf) of the Lindley distribution is defined by Lindley1 as follows
,
,
The distribution function (df) of the Lindley distribution is also defined as follows
,
,
Ghitany2 discussed the application of the Lindley distribution with a real-world dataset, after which the distribution became popular. Many generalizations of the Lindley distribution were developed. We redirect the readers to Tomy3 and Chesneau4 to get a better understanding of the different generalizations and applications of the Lindley distribution.
Among which the modified Lindley (ML) distribution developed by Chesneau5 is of prime importance. Suppose Y is a random variable following the ML distribution with parameter β, then the pdf of ML distribution is defined as follows
,
,
(1)
The df of the ML distribution are also defined as follows,
,
,
The mean and variance of ML distribution is given as follows,
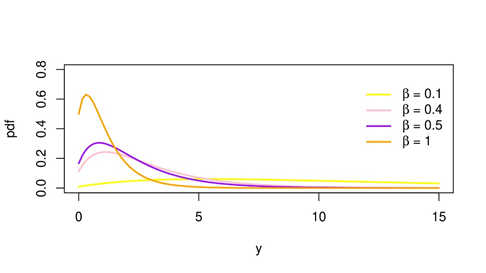
Figure 1 Illustrates the plots of the ML distribution with various values of the parameter β.
Observations –
The shapes of the pdf plots are unimodal, and are decreasing in nature.
In this paper, we discuss the different methods to estimate the unknown single parameter β of the ML distribution. A simulation study is also conducted to compare the efficiency of different estimators.
The structure of the paper is as follows. Section 2 discusses the different methods of estimating β. In Section 3, we compare the efficiency of the estimates produced by the different methods of estimation. Section 4 shows the application of different estimation methods over a real-world dataset.
Inferential aspects
In this section, we concentrate on the estimation of parameter β, with an assumption that β is unknown. Here, we consider estimating the parameter of the ML distribution using the methods, which include Maximum Likelihood (ML), Method of Moment (MOM) estimation, least squares (LS) and Weighted Least squares (WLS) estimation, and Cram´er-von Mises (CVM) estimation.
ML estimation
Consider (y1, y2, ..., yn) to be a random sample from the ML distribution with parameter , with pdf defined in Equation (1). The log-likelihood (LL) function is given by
The ML estimate of β,
is defined as
The ML estimate of β can be obtained by taking the derivative of LL(β) and equating it to zero, which is as follows:
As there doesn’t exist any explicit form of β, numerical methods are used to get the estimate of.
MOM estimation
Let (y1, y2, ..., yn) represent n independent ML distribution observations. Chesneau5 showed that the unique MoM estimate of the pdf defined in Equation, , of is given by
,
LS and WLS estimation
Swain6 devised the method of least squares. The difference between both the vector of uniformized order statistics and the associated vector of expected values is reduced using this approach. Let (y1, y2, ..., yn) represent a random sample from the ML distribution with parameters. Also, let y(1), y(2), … y(n) be the order values of y1,y2,...,yn in ascending order.
The LS estimate of is defined by
After partially differentiating with regard to unknown parameter β, one can construct a nonlinear equation using the df of the ML distribution. The Monte Carlo simulation can be used to find the solution to this nonlinear equation.
The WLS function is given as follows:
where
The WLS estimate of β is defined by
As a result, the WLS estimate of can be derived using a process similar to the LS estimate.
CVM estimation
The CVM approach is identical to the two methods earlier described. The CVM function is described as follows:
The CVM estimate of β is defined by
As a result, the CVM estimate of follows the same approach as the WL or LS estimations.
Simulation study
We conduct a simulation analysis in this part to assess the efficiency of the ML model parameter estimates reported in Section 3. We employed the Monte Carlo technique in R software, as well as Newton's method and the BFGS (Broyden-Fletcher-Goldfarb-Shanno) algorithm, developed by Broyden7, Fletcher8, Goldfarb9, & Shanno10.
The bias and Mean Square Error (MSE) were examined in the study,
Bias
and
.
where, for each sample size n, J
is the parameter's estimate at the jth iteration using a specific estimation method. R software, version 4.0.5, was used for all calculations.
Tables 1–3 show the biases and mean square error (MSE) of the proposed model's parameters based on N = 5000 replicates. To further analyse the nature of the estimates, various sample sizes (n = 50, 100, 200, and 500) and values of the parameters, β= (0.5,1,1.5) are employed.
n |
Estimate |
Bias |
MSE |
|
|
β |
50 |
ML |
0.017219 |
0.004665 |
|
MOM |
0.017282 |
0.004002 |
|
OLS |
0.016243 |
0.004623 |
|
WLS |
-0.5 |
0.25 |
|
CVM |
0.016524 |
0.003894 |
100 |
ML |
0.013654 |
0.00199 |
|
MOM |
0.013417 |
0.002018 |
|
OLS |
0.013752 |
0.00229 |
|
WLS |
-0.5 |
0.25 |
|
CVM |
0.013256 |
0.002306 |
200 |
ML |
0.011259 |
0.000995 |
|
MOM |
0.012063 |
0.001168 |
|
OLS |
0.011815 |
0.001161 |
|
WLS |
-0.5 |
0.25 |
|
CVM |
0.010682 |
0.000978 |
500 |
ML |
0.010423 |
0.000425 |
|
MOM |
0.011379 |
0.000505 |
|
OLS |
0.011279 |
0.000503 |
|
WLS |
-0.5 |
0.25 |
|
CVM |
0.010103 |
0.000422 |
Table 1 Bias and MSE for β = 0.5
n |
Estimate |
Bias |
MSE |
|
|
β |
|
50 |
ML |
0.03443951 |
0.0156625 |
|
MOM |
0.03748674 |
0.0162677 |
|
OLS |
0.02567615 |
0.01804344 |
|
WLS |
-1 |
1 |
|
CVM |
0.02774687 |
0.0181966 |
100 |
ML |
0.02801196 |
0.008132881 |
|
MOM |
0.0302575 |
0.00823406 |
|
OLS |
0.02086761 |
0.008980337 |
|
WLS |
-1 |
1 |
|
CVM |
0.02191171 |
0.009037173 |
200 |
ML |
0.02473895 |
0.003989069 |
|
MOM |
0.02688922 |
0.004123211 |
|
OLS |
0.01902113 |
0.004393245 |
|
WLS |
-1 |
1 |
|
CVM |
0.0195463 |
0.004416063 |
500 |
ML |
0.0234787 |
0.001838779 |
|
MOM |
0.02486852 |
0.001912136 |
Table 2 Bias and MSE for β = 1
n |
Estimate |
Bias |
MSE |
|
|
β |
50 |
ML |
0.1781775 |
0.07687606 |
|
MOM |
0.1962871 |
0.09591677 |
|
OLS |
0.1927908 |
0.09444386 |
|
WLS |
-1.5 |
2.25 |
|
CVM |
0.17634 |
0.07521178 |
100 |
ML |
0.1664498 |
0.04858995 |
|
MOM |
0.16478 |
0.04814568 |
|
OLS |
0.1813909 |
0.05871948 |
|
WLS |
-1.5 |
2.25 |
|
CVM |
0.02191171 |
0.009037173 |
200 |
ML |
0.1617356 |
0.03610189 |
|
MOM |
0.1784734 |
0.04441311 |
|
OLS |
0.1775813 |
0.04408753 |
|
WLS |
-1.5 |
2.25 |
|
CVM |
0. 02113903 |
0.003554184 |
500 |
ML |
0.1588387 |
0.02905477 |
|
MOM |
0.1753744 |
0.03550387 |
|
OLS |
0.1750164 |
0.03537724 |
|
WLS |
-1.5 |
2.25 |
|
CVM |
0.0155954 |
0.00281068 |
Table 3 Bias and MSE for β = 1.5
Some observations from Tables 1-3,
- The estimators of all the parameters are positively biased, except for the WLS estimator.
- The biases of all the estimators tend to zero for large values of the sample size n.
- WLS has the largest MSE among the considered four estimators.
- The CVM estimator has the least bias among all the other estimators.
Real data analysis
We use a well-known real data set to demonstrate the ML model's use in real-life circumstances. To accomplish this, we compare the estimates obtained through the different estimation methods of the ML model . Standard performance validation criteria such the goodness-of-fit testing statistic such as the Kolmogorov Smirnov (K-S), also denoted by Dn, are used to discover the best model.
The p-values for the KS test statistic are also taken into account. The best method of estimation has the smallest KS, as well as the highest p-values. We refer the readers to Kenneth and Anderson11 for definitions and more insights on these attributes. The data set includes 30 measurements of precipitation in March in Minneapolis, with inch as the unit of measurement. Hinkley12 has provided this data set.
Table 4 contains the parameter estimates obtained using various estimation methods for the ML distribution in order to complete the comparison of the estimation methods of the ML distribution.
Methods |
β |
K-S |
p-value |
MOM |
0.685563 |
0.167852 |
0.366565 |
OLS |
0.613856 |
0.129532 |
0.69541 |
WLS |
0.616286 |
0.130844 |
0.683348 |
CVM |
0.604734 |
0.124597 |
0.740227 |
MLE |
0.6644 |
0.1567 |
0.4532 |
Table 4 β of different estimation methods for ML distribution with K-S statistic and p-value
We use the essential metrics to compare the four estimation approaches for the weighted Lindley distribution:
- The K-S test with the highest p-value (which considers the greatest difference between the theoretical and empirical distributions)
Table 4 demonstrates that the CVM approach meets the above-mentioned criteria, namely, the highest p-values for the K–S test. As a result, we can conclude that the CVM estimation approach is the best appropriate among the five estimate methods for the presented data set.


